MODEL-BASED CAVITY SHAPE ESTIMATION IN A GAS-LIQUID
SYSTEM WITH NONUNIFORM IMAGE SAMPLING
Magnus Evestedt
Department of Information Technology, Uppsala University
P.O. Box 337, SE-951 05, Sweden
Alexander Medvedev
Department of Information Technology, Uppsala University
P.O. Box 337, SE-951 05, Sweden
Keywords:
Image analysis, feature extraction, model-based application, image sampling.
Abstract:
A water model is studied to simulate physical phenomena in the Lintz-Donawitz steel converter. The depres-
sion in the liquid, due to the impinging gas jet, is measured by means of a video camera. Image processing
tools are used to extract the edge of the surface indentation. The measured edge, sampled in a special way,
is used together with a nonlinear mathematical model to obtain a description of the cavity profile. The para-
meters of the mathematical model are optimized to match the registered cavity edge in the image at a set of
sampled points. Three ways of choosing sampling points for the optimization are proposed and compared on
simulated as well as experimental data. An approach involving an observer decreases the computation time
with an acceptable loss of accuracy of the estimates.
1 INTRODUCTION
The properties of a system consisting of a gas jet im-
pinging on a liquid surface from above are important
in many industrial applications. The focus of this pa-
per is on a steel making process involving top blowing
e.g. the Lintz-Donawitz (LD) converter. It is widely
used and stands for 60% of the world steel production,
(www.steel.org, 2005).
In the LD converter process, hot metal is converted
into steel by a top blown basic oxygen furnace. Scrap
and slag forming agents are added to the hot metal be-
fore oxygen is blown onto the metal bath, from above,
at supersonic speed. A cavity is formed where the
oxygen jet hits the bath surface and Fe, Si, Mn and C
are oxidized. The jetting also produces large amounts
of slag, where most of the chemical reactions take
place.
The lance position over the bath, together with the
oxygen flow rate are usually used as manipulated vari-
ables in the process. A deeper understanding of the
system of the gas jet and the liquid surface would im-
prove the efficiency of blowing and the control of the
process. The important parameters, determining heat
and mass transport at the interface and in the liquid,
are the interface shape, the width and depth of the cav-
ity and the height of the peripheral lip, (Eletribi et al.,
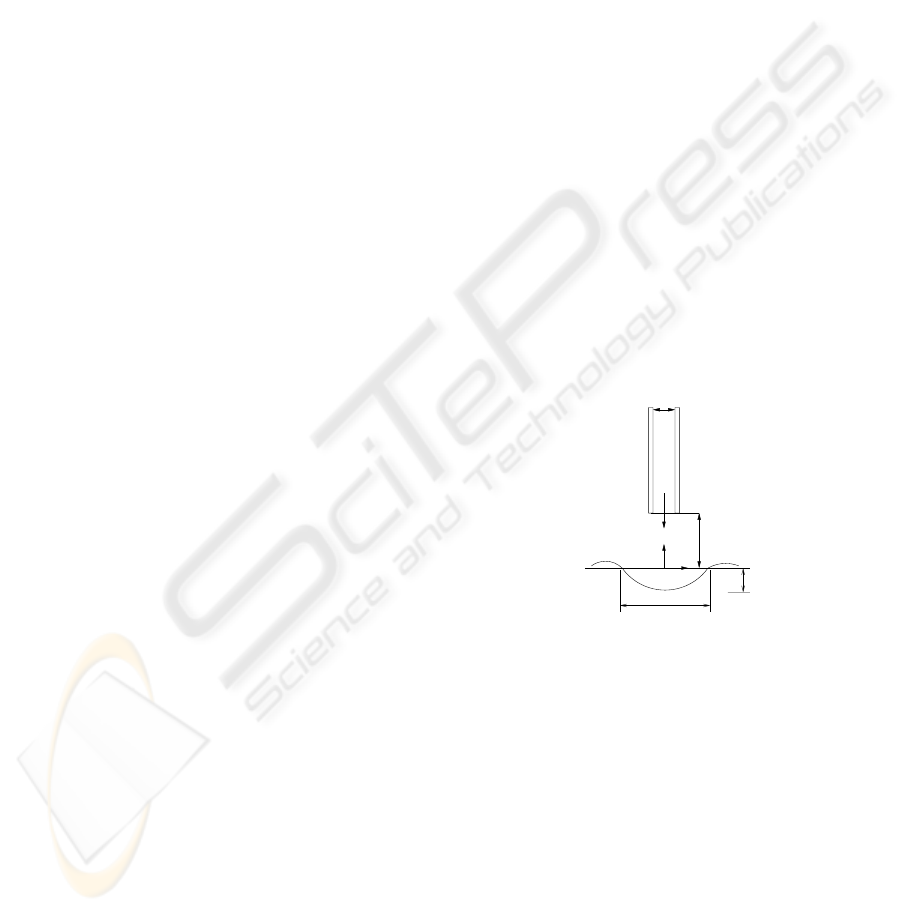
1997), see Figure1. The diameter of the lance is de-
d
V
j
h
r
H
D
h
0
Figure 1: Gas jet impinging on a liquid surface.
noted by d, the maximum velocity of the gas V
j
and
H is the lance height above the liquid surface. D and
h
0
are the diameter and depth, respectively, and h and
r define the axes in the coordinate system.
Depending on the properties of the gas jet and the
liquid, three modes of surface deformation have been
identified in the process: dimpling, splashing and
penetrating, (Molloy, 1970). These modes are illus-
trated in Figure 2. Only the first two modes are con-
sidered in the sequel.
Since the form of the cavity is difficult to observe
in the actual process, due to the hostile environment, a
water model of the LD converter is often used. In the
365
Evestedt M. and Medvedev A. (2006).
MODEL-BASED CAVITY SHAPE ESTIMATION IN A GAS-LIQUID SYSTEM WITH NONUNIFORM IMAGE SAMPLING.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 365-370
DOI: 10.5220/0001367503650370
Copyright
c
SciTePress

(a) (b) (c)
Figure 2: Modes of surface deformation by the imping-
ing gas jet according to (Molloy, 1970). (a) Dimpling, (b)
Splashing, (c) Penetrating.
water model the molten steel is replaced by water and
compressed air is used instead of oxygen. The sim-
ilarities between the water bath and the molten steel
are analyzed in (Lee et al., 2002).
Energy and force balances were considered in
(Rosler and Stewart, 1968), to describe the indenta-
tion profile. The results were later used in (Bergh-
mans, 1972), for a study of the stability of interfaces
between fluids in motion.
In (Evestedt and Medvedev, 2005) the cavity sur-
face model in (Berghmans, 1972) was used, together
with experimental data from a water model, to ap-
proximate the surface deformation and to quantify the
uncertainty of the depth and diameter estimates. The
uncertainty was shown to decrease when the tempo-
ral dynamics of the cavity were modelled as a sum of
sine waves.
In this paper a sampling algorithm to improve the
efficiency of the estimation procedure in (Evestedt
and Medvedev, 2005) is given. The paper is orga-
nized as follows: First a system model is introduced.
Then three approaches to choosing sampling points
for the optimization are presented, followed by a de-
scription of the experimental setup. The paper is con-
cluded with a comparison between the methods using
both simulated and experimental data.
2 PROBLEM FORMULATION
In (Berghmans, 1972) a mathematical model for the
gas-jet system was suggested. The model was in-
vestigated further in (Evestedt and Medvedev, 2005),
where it was reformulated in state-space form as
dx
dr
= f(r, x)= (1)
x
2
1
σ
(∆p +(ρ
1
− ρ
2
)gx
1
) 1+x
2
2
3
2
−
δ
r
x
2
1+x
2
2
x =[x
1
x
2
]
T
where x
1
= h, x
2
=
dh
dr
, g is the gravitational con-
stant, ∆p is the over-pressure due to the impinging
jet, δ =1, ρ
1
and ρ
2
are the densities of the liquid and
the gas, respectively and σ is the surface tension of
the specific liquid-gas combination.
To determine ∆p, Rosler and Stewart used the ex-
perimental data of Gibson, for laminar jets impinging
on a flat plate, (Gibson, 1934). The pressure distribu-
tion is approximated by:
∆p =
p
max
cos(0.826
r
r
j
) for r ≤ 1.2r
j
4.53p
max
exp(−1.76
r
r
j
) for r>1.2r
j
where r
j
is the jet radius, p
max
=
1
2
ρ
1
V
2
j
is the jet
strength and V
j
is the maximum jet velocity. In the
following, δ, σ and x
1
(0) are treated as tuning para-
meters.
The problem treated in this paper is then to estimate
the parameters θ =[δ, σ, x
1
(0)] in (1) from a video
sequence showing the liquid formation on the surface
of a water tank.
The cavity edge is extracted from the image frames.
Each point on the edge is assigned a coordinate (i, j)
describing its position in the image. A conversion
from the image coordinates (i, j) to actual coordi-
nates (h(r),r) is performed via image calibration.
Define a set of coordinates as M ∈ R
2
, and N as the
number of pixels in the set (cardinal number of M ).
In (Evestedt and Medvedev, 2005), the following cri-
terion function is used to estimate the parameters in
(1) by optimization.
ˆ
θ = arg min
θ
L(θ) (2)
L(θ)=
1
N
r∈M
(h(r) −
ˆ
h(r))
2
where
ˆ
h(r) is the model output.
The optimization is performed over the set M , us-
ing fminsearch in Matlab
c
. In the following, the
approach in (Evestedt and Medvedev, 2005), where
all data points, obtained by edge detection, belong to
M, will be referred to as Scheme 1.
The underlying algorithm for the multidimensional
unconstrained nonlinear minimization is the Nelder-
Mead search, (Nelder and Mead, 1965). It is based on
evaluating a function at the vertices of a simplex or
hypertetrahedron, then iteratively shrinking the sim-
plex as better points are found until some desired
bound is achieved. Due to the lack of convergence
results, the efficiency and complexity of the Nelder-
Mead search algorithm are hard to estimate, (Singer
and Singer, 2004). In this particular application, the
time needed for the algorithm to converge is depen-
dent on the number and placement of the data used in
the parameter tuning.
The contribution of this paper is two model-based
approaches to choose the sampling points used in the
optimization in such a way that the computation time
is substantially decreased, with acceptable reduction
of the estimation accuracy.
VISAPP 2006 - IMAGE ANALYSIS
366
3 PARAMETER ESTIMATION
In this section, two alternative model-based ap-
proaches to decrease the computation time of the op-
timization, by utilizing the data that contain most in-
formation about the edge, are presented. The schemes
are based on the vital assumption that the cavity shape
does not change abruptly from one frame to another.
3.1 Sampling
The continuous model described by Equation (1) is
nonlinear. There is no general theory regarding sam-
pling of nonlinear systems that can be applied directly
in this case. Consider a linear second order homo-
geneous ordinary differential equation, which can be
seen as a linearization of (1)
y
(t)+ay
(t)+by(t)=0 (3)
where the parameters a and b are constant real coeffi-
cients. Let a solution to Equation (3), (cf. Simmons,
1991) , be given by
y(t)=C
1
e
λ
1
t
+ C
2
e
λ
2
t
(4)
where λ
1
and λ
2
are negative real numbers and λ
1
=
λ
2
given by
λ
1,2
= −
a
2
±
a
2
4
− b (5)
In order to obtain a spectrum describing the distri-
bution of energy over frequency, ω, Equation (4) is
readily Fourier transformed to obtain
|Y (ω)|
2
=
C
1
jω − λ
1
+
C
2
jω − λ
2
2
(6)
According to the sampling theorem (cf Oppenheim
and Schafer, 1989) , a band-limited signal (i.e. one
with a zero spectrum for frequencies ω>ω
B
), can
be fully reconstructed from its sampled version, if the
sampling rate is chosen at least twice as large, that is
2ω
B
. Normally a much higher sampling rate is rec-
ommended, (
˚
Astr
¨
om and Wittenmark, 1997).
As can be seen in Equation (6), the spectrum de-
creases as
1
ω
2
. This property holds for all solutions to
(3). An important user choice when sampling Equa-
tion (4) is the threshold, ω
B
, above which the energy
content in the signal can be considered so small that
it can be neglected. The reconstruction accuracy is of
course highly dependent upon this choice.
The frequency content of the solution to the non-
linear Equation (1) is more difficult to characterize.
Here, a special feature is utilized, namely the fact that
the second state describes the derivative of the inden-
tation profile. Thus, it provides information on how
fast the curve changes. This property underlies the
following sampling methods.
3.2 An Ad-hoc Approach
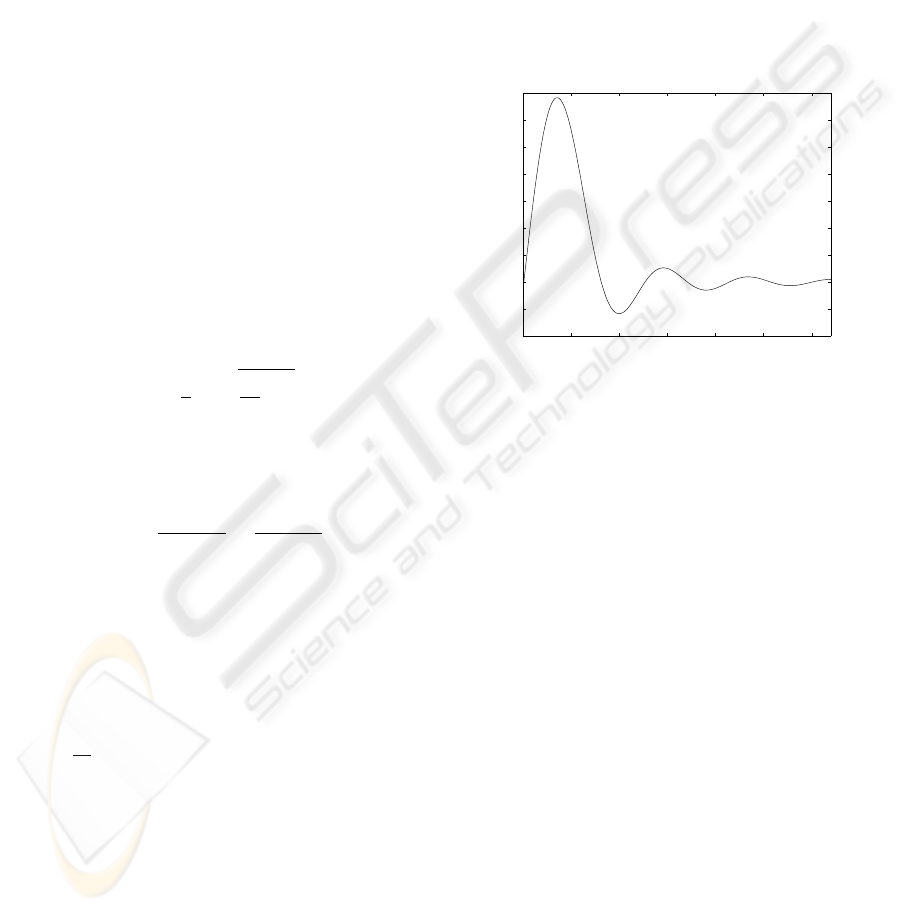
The most interesting points of the indentation profile
are where it changes most rapidly. Studying the deriv-
ative of the model adjusted to fit the measurement ob-
tained at time t in Figure 3, it can be seen that the
derivative decreases with increasing radial distance r
from the origin. The idea is to only use the points
where the derivative exceeds a user-defined thresh-
old in the optimization of the model parameters to the
measurement obtained at time t +1. Thus the amount
of data is reduced, decreasing the computation time.
0 2 4 6 8 10 12
−4
−2
0
2
4
6
8
10
12
14
x 10
−3
Derivative of h(r)
r [cm]
Figure 3: The derivative of the model edge.
A summary of the proposed approach is as follows:
Scheme 2
1. Define a threshold, T , for the derivative of the cav-
ity edge w.r.t. r.
2. Take the first frame in the video sequence and ex-
tract the edge of the cavity. Let all edge pixels con-
stitute the set M . Solve optimization problem (2).
3. Evaluate Equation (1) for the parameters
ˆ
θ(t) ob-
tained in the previous step to estimate the derivative
of the cavity edge w.r.t. r.
4. Find the pixels where the derivative is larger than a
user-defined threshold. Let those points constitute
M.
5. Retrieve the next image frame.
6. Detect the cavity edge.
7. Sample the detected edge only at the points in M
for the optimization.
8. Solve optimization problem (2) to obtain parameter
estimate
ˆ
θ(t).
9. Goto (3).
MODEL-BASED CAVITY SHAPE ESTIMATION IN A GAS-LIQUID SYSTEM WITH NONUNIFORM IMAGE
SAMPLING
367

Scheme 2 is thus model-based, but does not take
into account the data extracted from the current im-
age. In the next section a Kalman filter is used to
estimate the derivative of the model edge, based on
the new measurement, to improve the placing of the
sampling points.
3.3 A Kalman Filter Based Observer
Approach
In this approach the model of the surface at time t is
used together with the new measurement at time t +1
to estimate the derivative of the indentation profile.
The estimation is performed using the Kalman filter.
To fit nonlinear system (1) into the Kalman filter
framework, it is expanded in first order Taylor series
around estimates of x(r). The linearization is as fol-
lows
f(r, x) ≈ f(r, ˆx)+F (r)(x − ˆx) (7)
where
F (r)=
∂f(r, x)
∂x
|
x=ˆx
(8)
(9)
and the linearized system is
dx
dr
= F (r)x(r)+u(r)+w(r) (10)
u(r)=f(r, ˆx) − F (r)ˆx (11)
y(r)=x
1
+ v(r) (12)
where w(r) and v(r) correspond to modelling errors
and measurement errors, respectively. It is assumed
that w(r) and v(r) are white noise sequences with
variances R
1
and R
2
.
Now, the Kalman filter can be used as an observer
of the process. The continuous Kalman filter equa-
tions are
dˆx
dr
= F (r)ˆx + u(r)+K(r)(y(r) − ˆx
1
(r)) (13)
dP
dr
= F (r)P (r)+P (r)F
T
(r)+R
1
(14)
− K(r)R
2
K
T
(r)
K(r)=P (r)[1 0]
T
R
−1
2
(15)
where y(r) in the correction term of (13) is cal-
culated using linear interpolation between subsequent
pixels.
The observer based approach can be summarized
as follows:
Scheme 3
1. Define a threshold, T , for the derivative of the cav-
ity edge w.r.t. r.
2. Take the first frame in the video sequence and ex-
tract the edge of the cavity. Let all edge pixels con-
stitute the set M . Solve optimization problem (2).
3. Estimate the derivative of the cavity edge w.r.t. r
from the measurement obtained at time t +1, us-
ing the observer (13)-(15) based on the model from
time t with the current estimate
ˆ
θ(t).
4. Find the pixels where the derivative estimate is
larger than a user-defined threshold. Let those
points constitute M.
5. Retrieve the next image frame.
6. Detect the cavity edge.
7. Sample the detected edge only at the points in M
for the optimization.
8. Solve optimization problem (2) to obtain parameter
estimate
ˆ
θ(t).
9. Goto (3).
4 EXPERIMENTAL SETUP
The experiments in Subsection 5.2 were conducted on
a water model of the LD converter, previously used to
study and control foaming, (Birk et al., 2003), and
to characterize the shape of the cavity, (Evestedt and
Medvedev, 2005). A single hole cylindrical nozzle
with diameter 1.5 mm was used. The indentation pro-
file arising when air is jetted onto the liquid surface
was recorded using a CCD camera. An example of
a photograph taken with the camera together with an
approximation of the cavity edge by Equation (1) is
shown in Figure 4.
Figure 4: Photograph of the water surface during a blow. An
approximation of the cavity edge is included in the image.
VISAPP 2006 - IMAGE ANALYSIS
368

4.1 Image Processing
To extract the edges from the photographs an in-house
software was used, previously employed in (Evestedt
and Medvedev, 2005). The frames of the video se-
quence are filtered to reduce the noise in the image.
Then edge detection is applied using a thresholding
method, together with some basic image processing
tools such as opening, closing and flood-fill, (Sonka
et al., 1999).
4.2 Sources of Error
There are several sources of error in the experimental
setup.
• The oxygen flow through the lance is slowly vary-
ing with time.
• The lance angle to the water bath cannot be guar-
anteed to be 90 degrees.
• Bubbles and splashing make the edge detection dif-
ficult.
5 RESULTS
In this section the three optimization approaches are
compared to each other in terms of approximation ac-
curacy, computation time and data utilization. The
comparison is performed on simulated as well as ex-
perimental data.
5.1 Simulation Results
A sequence of 50 ideal edges obtained from Equa-
tion (1) was used to study the performances of the
considered methods. The edge was corrupted using a
white sequence to simulate the random error sources.
The parameters, θ, were varied in a manner similar to
that observed in experiments.
The three optimization schemes were employed to
find estimates,
ˆ
θ, of the parameters. Since the para-
meters are not constant, the estimation error
˜
θ(t)=
θ(t) −
ˆ
θ(t) is used as a measure of estimation accu-
racy. In Table 1 the mean value of the ratio between
the estimation error and the true parameter is shown
in percent. The mean performance in terms of time
and data utilization is shown in Table 2.
As can be seen x
1
(0) is accurately estimated for all
considered methods. The parameters δ and σ seem
to be more difficult to estimate, which is indicated
by larger estimation errors. Scheme 3 however, pro-
vides estimates of reasonable accuracy compared to
Scheme 1. Better accuracy can be obtained by lower-
ing the sampling threshold and thus considering more
Table 1: The estimation accuracy of the considered schemes
given as the mean value of the ratio between the estimation
errors,
˜
θ and the true parameter values in θ, shown in %.
Scheme 1 Scheme 2 Scheme 3
˜
δ/δ
0.38 3.11 1.90
˜σ/σ 7.09 22.0 12.2
˜x
1
(0)/x
1
(0) 0.56 0.63 0.63
Table 2: The mean performance in terms of approximation
accuracy, time and data utilization for the three approaches.
Simulated data.
Scheme 1 Scheme 2 Scheme 3
Time [s] 16.7 8.97 4.4
Data [%] 100 25 24
edge points in the estimation. The most significant
gain of using Scheme 2 over Scheme 1 is in reduc-
tion of the optimization time. If Scheme 3 is used
instead, the computation time is decreased even fur-
ther, with higher estimation accuracy compared to
Scheme 2. From Table 2 it follows that the compu-
tation time using Scheme 3 is just a quarter of the one
using Scheme 1.
5.2 Experiments
A sequence of 50 frames was obtained experimentally
using the water model setup, with a lance height of 12
cm and a gas flow rate of 21 l/min. Image process-
ing techniques were utilized to obtain the edge of
the cavity. The three approaches, Schemes 1, 2 and
Scheme 3, were used to approximate the measured
edge.
Since true model parameter values are unknown in
the experiments, Equation (2) is used as a measure
of how well the cavity form is approximated. The
full edge measurement is considered as the true edge,
h(r), in the loss function L(θ). In Figure 5, the
estimation accuracy of the optimization approaches
are shown. As can be seen, the reduction of data
points does not significantly affect the accuracy of the
approximation, except at the locations of the peaks.
It is likely that splashing water in the tank destroys
the edge detection and invalidates the model at these
points. The best approximation is naturally the ap-
proach using all the measured data.
The mean performance in terms of time, approxi-
mation accuracy and data utilization is shown in Ta-
ble 3. The large peaks for some of the edge real-
izations affect the mean values significantly, explain-
ing the large mean values of L(θ) in Scheme 2 and
Scheme 3.
MODEL-BASED CAVITY SHAPE ESTIMATION IN A GAS-LIQUID SYSTEM WITH NONUNIFORM IMAGE
SAMPLING
369

Table 3: The mean performance in terms of approximation
accuracy, time and data utilization for the three approaches.
Experimental data.
Scheme 1 Scheme 2 Scheme 3
L 0.015 13.6 0.41
Time [s] 38.5 33.3 27.4
Data [%] 100 63 61
0 5 10 15 20 25 30 35 40 45 5
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Frame
L
Scheme 1
Scheme 2
Scheme 3
Figure 5: The approximation accuracy for the three opti-
mization approaches using 50 realizations of the edge.
6 CONCLUSIONS
Two approaches to selecting sampling points in a
nonuniform way in the images of a surface cavity in
a water model were proposed. Instead of using all the
data points, a smaller number of data was utilized and
shown both on simulated as well as on experimental
data to decrease the computation time with an accept-
able reduction of the estimation accuracy.
ACKNOWLEDGMENTS
This work has been in part supported by The
Swedish Steel Producers’ Association and by the
EC 6th Framework programme as a Specific Tar-
geted Research or Innovation Project (Contract num-
ber NMP2-CT-2003-505467).
REFERENCES
Berghmans, J. (1972). Theoretical investigation of the inter-
facial stability of inviscid fluids in motion, considering
surface tension. Journal of Fluid Mechanics, 54:129–
141.
Birk, W., Arvanitidis, I., J
¨
onsson, P., and Medvedev, A.
(2003). Foam level control in a water model of the
LD converter process. Control Engineering Practice,
11:49–56.
Eletribi, S., Mukherjee, D. K., and Prasad, V. (1997). Exper-
iments on liquid surface deformation upon impinge-
ment by a gas jet. In Proceedings of the ASME Fluids
Engineering Division, volume 244.
Evestedt, M. and Medvedev, A. (2005). Gas jet impinging
on liquid surface: Cavity shape modelling and estima-
tion. In Proceedings of the 16th IFAC World Congress.
Gibson, A. H. (1934). Hydraulics and Its Application. Lon-
don:Constable.
Lee, M. S., O´Rourke, S. L., and Molloy, N. A. (2002).
Fluid flow and surface waves in the BOF. ISS Trans-
actions, 29(10):56–65.
Molloy, N. A. (1970). Impinging jet flow in a two-phase
system:the basic flow pattern. Journal of the iron and
steel institute, pages 943–950.
Nelder, J. A. and Mead, R. (1965). A simplex method
for function minimization. Computer Journal, 7:308–
313.
Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time
Signal Processing. Prentice Hall.
Rosler, R. S. and Stewart, G. H. (1968). Impingement of gas
jets on liquid surfaces. Journal of Fluid Mechanics,
31:163–174.
Simmons, G. F. (1991). Differential equations with appli-
cations and historical notes. McGraw Hill, Inc.
Singer, S. and Singer, S. (2004). Efficient implementation
of the Nelder-Mead search algorithm. Applied Numer-
ical Analysis & Computational Mathematics, 1:524–
534.
Sonka, M., Hlavac, V., and Boyle, R. (1999). Image
processing, analysis and machine vision. PWS Pub-
lishing.
˚
Astr
¨
om, K. J. and Wittenmark, B. (1997). Computer-
controlled systems. Prentice Hall.
www.steel.org (2005). Steel industry technology roadmap.
www.steel.org.
VISAPP 2006 - IMAGE ANALYSIS
370
