IMPROVED RECONSTRUCTION OF IMAGES

DISTORTED BY WATER WAVES

Arturo Donate and Eraldo Ribeiro

Department of Computer Sciences

Florida Institute of Technology

Melbourne, FL 32901

Keywords:

Image recovery, reconstruction, distortion, refraction, motion blur, water waves, frequency domain.

Abstract:

This paper describes a new method for removing geometric distortion in images of submerged objects observed

from outside shallow water. We focus on the problem of analyzing video sequences when the water surface

is disturbed by waves. The water waves will affect the appearance of the individual video frames such that

no single frame is completely free of geometric distortion. This suggests that, in principle, it is possible to

perform a selection of a set of low distortion sub-regions from each video frame and combine them to form

a single undistorted image of the observed object. The novel contribution in this paper is to u se a multi-

stage clustering algorithm combined with frequency domain measurements that allow us to select the best

set of undistorted sub-regions of each frame in the video sequence. We evaluate the new algorithm on video

sequences created both in our laboratory, as well as in natural environments. Results show that our algorithm

is effective in removing distortion caused by water motion.

1 INTRODUCTION

In this paper, we focus on the problem of recovering

a single undistorted image from a set of non-linearly

distorted images. More speciﬁcally, we are interested

in the case where an object submerged in water is

observed by a video camera from a static viewpoint

above the water. The water surface is assumed to

be disturbed by waves. Figure 1 shows a sample of

frames from a video of a submerged object viewed

from above. This is an interesting and difﬁcult prob-

lem mainly when the geometry of the scene is un-

known. The overall level of distortion in each frame

depends on three main parameters of the wave model:

the amplitude, the speed of oscillation, and the slope

of the local normal vector on the water surface. The

amplitude and slope of the surface normal affect the

refraction of the viewing rays causing geometric dis-

tortions while the speed of oscillation causes motion

blur due to limited video frame rate.

Our goal in this paper is to recover an undistorted

image of the underwater object given only a video of

the object as input. Additionally, no previous knowl-

edge of the waves or the underwater object is as-

sumed. We propose to model the geometric distor-

tions and the motion blur separately from each other.

Figure 1: An arbitrary selection of frames from our low

energy wave data set.

We analyse geometric distortions via clustering, while

measuring the amount of motion blur by analysis in

the frequency domain in an attempt to separate high

and low distortion regions. Once these regions are

acquired, we combine single samples of neighboring

low distortion regions to form a single image that best

represents the object.

We test our method on different data sets created

both in the laboratory as well as outdoors. Each

experiment has waves of different amplitudes and

speeds, in order to better illustrate its robustness. Our

current experiments show very promising results.

The remainder of the paper is organized as follows.

We present a review of the literature in Section 2. In

228

Donate A. and Ribeiro E. (2006).

IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 228-235

DOI: 10.5220/0001369202280235

 SciTePress

Section 3, we describe the geometry of refraction dis-

tortion due to surface waves. Section 4 describes the

details of our method. In Section 5, we demonstrate

our algorithm on video sequences acquired in the lab-

oratory and outdoors. Finally, in Section 6, we present

our conclusions and directions for future work.

2 RELATED WORK

Several authors have attempted to approach the gen-

eral problem of analyzing images distorted by wa-

ter waves. The dynamic nature of the problem re-

quires the use of video sequences of the target scene

as a primary source of information. In the discussion

and analysis that follow in this paper, we assume that

frames from an acquired video are available.

The literature has contributions by researchers in

various ﬁelds including computer graphics, computer

vision, and ocean engineering. Computer graphics

researchers have primarily focused on the problem

of rendering and reconstructing the surface of the

water (Gamito and Musgrave, 2002; Premoze and

Ashikhmin, 2001). Ocean engineering researchers

have studied sea surface statistics and light refrac-

tion (Walker, 1994) as well as numerical modeling of

surface waves (Young, 1999). The vision community

has attempted to study light refraction between water

and materials (Mall and da Vitoria Lobo, 1995), re-

cover water surface geometry (Murase, 1992), as well

as reconstruct images of submerged objects (Efros

et al., 2004; Shefer et al., 2001). In this paper, we

focus on the problem of recovering images with min-

imum distortion.

A simple approach to the reconstruction of images

of submerged objects is to perform a temporal av-

erage of a large number of continuous video frames

acquired over an extended time duration (i.e., mean

value of each pixel over time) (Shefer et al., 2001).

This technique is based on the assumption that the

integral of the periodic function modeling the water

waves is zero (or constant) when time tends to in-

ﬁnity. Average-based methods such as the one de-

scribed in (Shefer et al., 2001) can produce reason-

able results when the distortion is caused by low en-

ergy waves (i.e., waves of low amplitude and low fre-

quency). However, this method does not work well

when the waves are of higher energy, as averaging

over all frames equally combines information from

both high and low distortion data. As a result, the av-

eraged image will appear blurry and the ﬁner details

will be lost.

Modeling the three-dimensional structure of the

waves also provides a way to solve the image recov-

ery problem. Murase (Murase, 1992) approaches the

problem by ﬁrst reconstructing the 3D geometry of

the waves from videos using optical ﬂow estimation.

He then uses the estimated optical ﬂow ﬁeld to cal-

culate the water surface normals over time. Once the

surface normals are known, both the 3D wave geom-

etry and the image of submerged objects are recon-

structed. Murase’s algorithm assumes that the water

depth is known, and the amplitude of the waves is low

enough that there is no separation or elimination of

features in the image frames. If these conditions are

not met, the resulting reconstruction will contain er-

rors mainly due to incorrect optical ﬂow extraction.

More recently, Efros et al. (Efros et al., 2004)

proposed a graph-based method that attempts to re-

cover images with minimum distortion from videos

of submerged objects. The main assumption is that

the underlying distribution of local image distortion

due to refraction is Gaussian shaped (Cox and Munk,

1956). Efros et al., propose to form an embedding of

subregions observed at a speciﬁc location over time

and then estimate the subregion that corresponds to

the center of the embedding. The Gaussian distor-

tion assumption implies that the local patch that is

closer to the mean is fronto-parallel to the camera and,

as a result, the underwater object should be clearly

observable through the water at that point in time.

The solution is given by selecting the local patches

that are the closest to the center of their embedding.

Efros et al., propose the use of a shortest path al-

gorithm that selects the solution as the frame hav-

ing the shortest overall path to all the other frames.

Distances were computed transitively using normal-

ized cross-correlation (NCC). Their method addresses

likely leakage problems caused by erroneous shortest-

distances between similar but blurred patches by cal-

culating paths using a convex ﬂow approach. The

sharpness of the image reconstruction achieved by

their algorithm is very high compared to average-

based methods even when applied to sequences dis-

torted by high energy waves.

In this paper we follow Efros et al. (Efros et al.,

2004), considering an ensemble of ﬁxed local regions

over the whole video sequence. However, our method

differs from theirs in two main ways. First, we pro-

pose to reduce the leakage problem by addressing the

motion blur effect and the refraction effect separately.

Second, we take a frequency domain approach to the

problem by quantifying the amount of motion blur

present in the local image regions based on measure-

ments of the total energy in high frequencies.

Our method aims at improving upon the basic

average-based techniques by attempting to separate

image subregions into high and low distortion groups.

The K-Means algorithm (Duda et al., 2000) is used

along with a frequency domain analysis for generat-

ing and distinguishing the two groups in terms of the

quality of their member frames. Normalized cross-

correlation is then used as a distance measurement to

IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES

229

ﬁnd the single frame that best represents the undis-

torted view of the region being analyzed.

3 DISTORTION ANALYSIS

In the problem considered in this paper, the local im-

age distortions caused by random surface waves can

be assumed to be modeled by a Gaussian distribu-

tion (Efros et al., 2004; Cox and Munk, 1956). The

magnitude of the distortion at a given image point in-

creases radially, forming a disk in which the center

point contains the least amount of distortion. The cen-

ter subregion can be determined by a clustering algo-

rithm if the distribution of the local patches is not too

broad (i.e., the diameter of the disk is small) (Efros

et al., 2004). Our method effectively reduces the size

of this distortion embedding by removing the sub-

regions containing large amounts of translation and

motion blur. In this section, we analyze how refrac-

tion and motion blur interferes with the appearance of

submerged objects observed from outside the water.

First, we analyze the geometry of refraction and its

relationship to both the surface normals of the waves

and the distance from the camera to the water. We

then analyze the motion blur distortion caused by the

speed of oscillation of the waves, and how it can be

quantiﬁed in the frequency domain.

3.1 Refraction Caused by Waves

Consider a planar object submerged in shallow trans-

parent water. The object is observed from a static

viewpoint above the water by a video camera with

optical axis perpendicular to the submerged planar

object. In our modeling, we assume that only the

water is moving in the scene (i.e., both the camera

and the underwater object are stationary). Addition-

ally, the depth of the object is assumed to be unknown

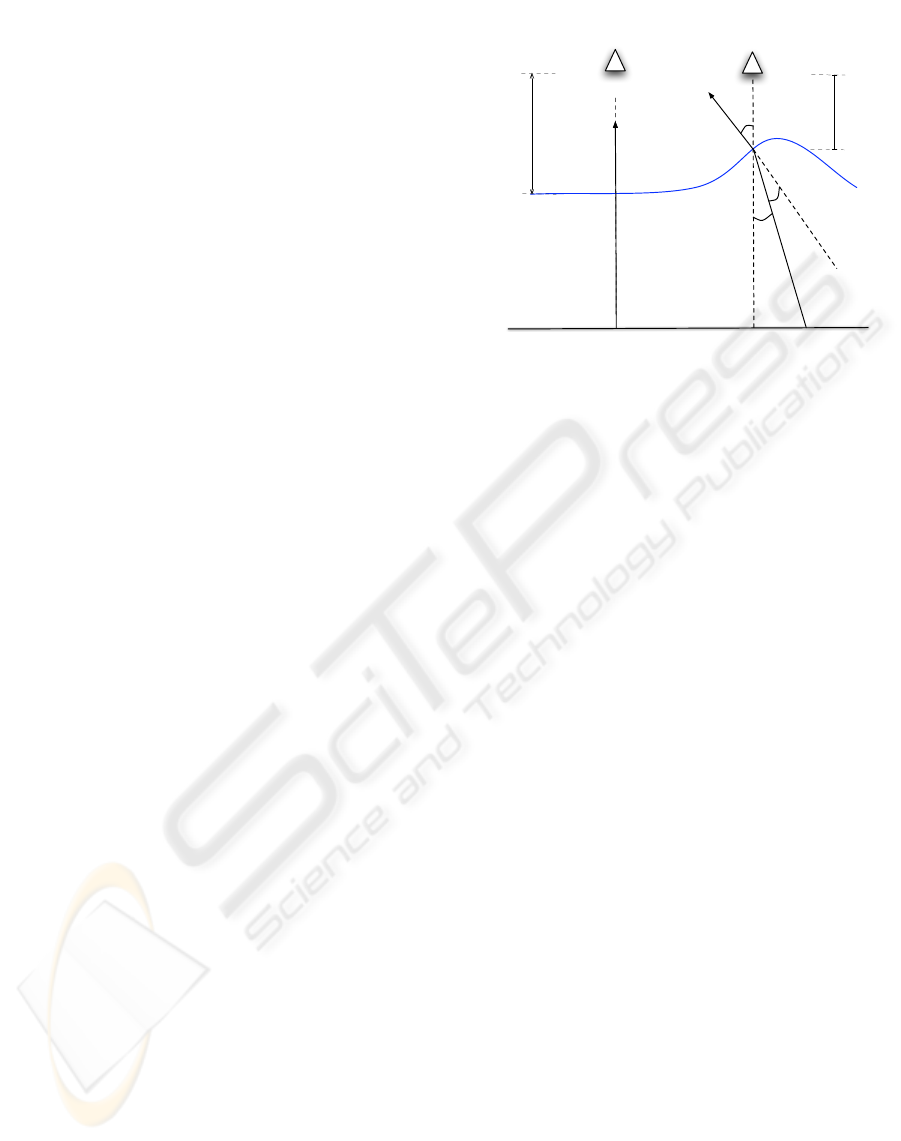
and constant. Figure 2 illustrates the geometry of the

scene. In the ﬁgure, d is the distance between the

camera and a point where the ray of light intersects

the water surface (i.e., point of refraction). The an-

gle between the viewing ray and the surface normal is

, and the angle between the refracted viewing ray

and the surface normal is θ

. These two angles are

related by Snell’s law (1). The camera c observes a

submerged point p. The angle α measures the rela-

tive translation of the point p when the viewing ray is

refracted by the water waves.

According to the diagram in Figure 2, the image

seen by the camera is distorted by refraction as a func-

tion of both the angle of the water surface normal at

the point of refraction and the amplitude of the water

waves. If the water is perfectly ﬂat (i.e., there are no

waves), there will be no distortion due to refraction.

p = p'

time = t

p p'

time = t + 1

Figure 2: Geometry of refraction on a surface disturbed by

waves. The camera c observes a given point p on the sub-

merged planar object. The slant angle of the surface normal

(θ

) and the distance from surface to the camera (d) are the

main parameters of our distortion model. When θ

is zero,

the camera observes the point p at its original location on

the object (i.e., there is no distortion in the image). If θ

changes, the apparent position of p changes by a transla-

tion factor with magnitude kp

− pk. This magnitude also

varies as a function of the distance from the water surface

to the camera (e.g., due to the amplitude of the waves). The

ﬁgure also illustrates the light refracting with the waves at

two different points in time. The image at time t would ap-

pear clear while the image at time t+1 would be distorted by

refraction.

However, if the surface of the water is being disturbed

by waves, the nature of the image distortion becomes

considerably more complex. In this paper, we will fo-

cus on the case where the imaged object is planar and

is parallel to the viewing plane (i.e., the planar object

is perpendicular to the optical axis of the camera).

In the experiments described in this paper, the main

parameters that model the spatial distortion in the im-

age are the slant angle of the surface normal (θ

) and

the distance from surface to the camera (d). The two

parameters affect the image appearance by translating

image pixels within a small local neighborhood. More

speciﬁcally, the varying slope of the waves and their

amplitude will modify the angle of refraction that will

result in the distortion of the ﬁnal image. Addition-

ally, considerable motion blur can occur in each video

frame due to both the limited capture frequency of

the video system, and the dynamic nature of the liq-

uid surface. The blur will have different magnitudes

across the image in each video frame. In our experi-

ments, varying levels of motion blur will be present in

each frame depending on the speed of change in the

slant of the surface normals. Next, we show that the

translation caused by refraction is linear with respect

VISAPP 2006 - IMAGE ANALYSIS

230

to the distance d and non-linear with respect to the

slant angle of the water surface normal (θ

We commence by modeling the refraction of the

viewing ray. The refraction of light from air to water

is given by Snell’s law as:

sin θ

= r

sin θ

(1)

where θ

is the angle of incidence of light. In our

case, θ

corresponds to the slant angle of the wa-

ter surface normal. θ

is the angle of refraction be-

tween the surface normal and the refracted viewing

ray. The air refraction coefﬁcient is assumed to be

the unit and r

is the water refraction coefﬁcient (r

= 1.33). From Figure 2, the angle that measures the

amount of translation when θ

varies is given by:

α = θ

− θ

(2)

Solving for θ

in Equation 1 and substituting the re-

sult into Equation 2 we have:

α = θ

− arcsin(

sin θ

) (3)

Considering the triangle 4opp

, the magnitude of the

underwater translation is given by:

− pk = d tan α (4)

From (3), the overall translation is:

− pk = d tan[θ

− arcsin(

sin θ

)] (5)

Equation 5 describes the translational distortion of

underwater points caused by two parameters: the slant

angle of the surface normal and the distance between

the camera and the point of refraction. The magnitude

of translation in (5) is linear with respect to d and non-

linear with respect to θ

. These two variables will

vary according to the movement of the water waves.

For a single sinusoidal wave pattern model, the am-

plitude of the wave will affect d while the slope of

the waves will affect the value of θ

. The distortion

modeled by Equation 5 vanishes when d = 0 (i.e., the

camera is underwater), or the angle θ

is zero (i.e., the

surface normal is aligned with the viewing direction).

3.2 Motion Blur and Frequency

Domain

Motion blur accounts for a large part of the distortion

in videos of submerged objects when the waves are of

high energy. The speed of oscillation of the surface

waves causes motion blur in each frame due to lim-

ited video frame rate. Studies have shown that an in-

crease in the amount of image blur decreases the total

high frequency energy in the image (Field and Brady,

1997).

Figure 3: Blur and its effect on the Fourier domain. Top

row: images with increasing levels of blur. Bottom row:

corresponding radial frequency histograms. Blur causes a

fast drop in energy in the radial spectral descriptor (decrease

in high frequency content).

Figure 3 shows some examples of regions with mo-

tion blur distortion (top row) and their corresponding

radial frequency histograms after a high-pass ﬁlter is

applied to the power spectrum (bottom row). The de-

crease of energy in high frequencies suggests that, in

principle, it is possible to determine the level of blur

in images of the same object by measuring the total

energy in high frequencies.

As pointed out in (Field and Brady, 1997), mea-

suring the decay of high-frequency energy alone does

not work well for quantifying motion blur of differ-

ent types of images, as a simple reduction of the to-

tal number of edges in an image will produce power

spectra with less energy in higher frequencies but no

decrease in the actual image sharpness. Alternatively,

blur in images from different scenes can be more ef-

fectively quantiﬁed using measures such as the phase

coherence described in (Wang and Simoncelli, 2004).

In this paper, we follow (Field and Brady, 1997) by

using a frequency domain approach to quantify the

amount of motion blur in an image. We use the to-

tal energy of high-frequencies as a measure of image

quality. This measurement is able to accurately quan-

tify relative blur when images are taken from the same

object or scene (e.g., images roughly containing the

same number of edges).

In order to detect the amount of blur present in a set

of images corresponding to the same region of the ob-

ject, we ﬁrst apply a high-pass ﬁlter to the power spec-

trum of each image. We express the ﬁltered power

spectrum in polar coordinates to produce a function

S(r, θ), where S is the spectrum function, r and θ

are the variables in this coordinate system. A global

description of the spectral energy can be obtained

by integrating the the polar power spectrum function

into 1D histograms as follows (Gonzalez and Woods,

1992):

S(r) =

θ=0

S(r, θ) (6)

IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES

231

Summing the high-frequency spectral energy in the

1D histograms provides us with a simple way to de-

termine changes in the level of blur when comparing

blurred versions of the same image. Figure 3 (bottom

row) shows a sample of radial frequency histograms.

The low frequency content in the histograms has been

ﬁltered out by the high-pass ﬁlter. The decrease in the

high-frequency energy corresponds to an increase on

the level of motion blur in the images.

4 METHOD OVERVIEW

Let us assume that we have a video sequence with

N frames of a submerged object. We commence

by sub-dividing all the video frames into K small

overlapping sub-regions (R

= {x

, . . . , x

}, k =

1, . . . , K). The input data of our algorithm consists

of these K sets of smaller videos describing the lo-

cal refraction distortion caused by waves on the ac-

tual large image. The key assumption here is that lo-

cal regions will sometimes appear undistorted as the

surface normal of the local plane that contains the re-

gion is aligned with the optical axis of the camera.

Our goal is to determine the local region frame in-

side each region dataset that is closest to that fronto-

parallel plane. We approach the problem by assuming

that there will be two main types of distortion in the

local dataset. The distortions are described in Sec-

tion 3. The ﬁrst type is the one caused by pure refrac-

tion driven by changes in both distance from the cam-

era to the water and the angle of the water surface nor-

mal. The second type of distortion is the motion blur

due to the speed of oscillation of the waves. Refrac-

tion and blur affect the local appearance of the frames

in distinct ways. The ﬁrst causes the local regions

to translate across neighboring sub-regions while the

second causes edges to become blurred. The exact in-

terplay between these two distortions is complex. The

idea in our algorithm is to quantify these distortions

and select a reduced set of high-quality images from

which we will choose the best representative region

frames.

We start by clustering each local dataset into groups

with the K-Means algorithm (Duda et al., 2000), us-

ing the Euclidean distance between the frames as a

similarity measure. Since no previous knowledge of

the scene is available, the K-Means centers were ini-

tialized with a random selection of sample subregions

from the dataset. The clustering procedure mainly

separates the frames distorted by translation. We ex-

pect the frames with less translation distortion to clus-

ter together. However, some of the resulting clus-

ters will contain frames with motion blur. In our ex-

periments, the Euclidean distance measurement has

shown good results in grouping most, if not all, of the

Algorithm 1 Multi-stage clustering.

Given N video frames:

1: Divide frames into K overlapping sub-regions.

2: Cluster each set of sub-regions to group the low

distortion frames.

3: Remove the images with high level of blur from

each group of low distortion frames.

4: Select the closest region to all other regions in

that set using cross-correlation.

5: Create a ﬁnal reconstructed single large image by

mosaicking all subregions.

6: Apply a blending technique to reduce tiling arti-

facts between neighboring regions.

lower distortion frames together, with some high dis-

tortion frames present. The initial number of clusters

is very important. We found that the more clusters

we could successfully split a data set into, the easier

it was for the rest of the algorithm to obtain a good

answer. To guarantee convergence, re-clustering was

performed when one of the clusters had less than 10%

of the total number of frames (e.g., in an 80-frame

data set, each of the four clusters must have at least

eight frames or we re-cluster the data). The algorithm

initially attempts to divide the data into 10 clusters. If

each cluster does not contain at least 10% of the total

number of frames after a certain number of iterations,

we reduce the number of clusters by one and repeat

the process until the data is successfully clustered.

We assume that one of the resulting clusters pro-

duced by the K-Means algorithm contains mostly low

distortion frames. To distinguish it from the other

clusters, we take a statistical approach by assuming

that the cluster containing most of the low distortion

frames has the least amount of pixel change across

frames. This is equivalent to saying that the frames

should be similar in appearance to each other. We

compute the variance of each pixel over all frames in

the cluster using

i=1

− ¯p)

(7)

where n is the number of frames in the cluster, p

the pixel value of the i-th image frame for that point,

and ¯p is the mean pixel value for that point over all

frames in the cluster. We take the sum of the vari-

ances of all the pixels for each cluster, and the clus-

ter with the minimum total variance is labeled as the

low distortion group. Our experiments show that this

technique is approximately 95% successful in distin-

guishing the best cluster. The algorithm discards all

frames that are not in the cluster with the lowest total

variance.

At this point, we have greatly reduced the number

of frames for each region. The next step of the al-

gorithm is to rank all frames in this reduced dataset

VISAPP 2006 - IMAGE ANALYSIS

232

with respect to their sharpness. As described in Sec-

tion 3, the Fourier spectrum of frames containing mo-

tion blur tend to present low energy in high frequency.

This allows us to remove the frames with high level of

blur by measuring the decay of high frequency energy

in the Fourier domain. We calculate the mean energy

of all frame regions and discard the ones whose en-

ergy is less than the mean.

Finally, the algorithm produces a subset of frame

regions which are similar in appearance to each other

and have small amounts of motion blur. We then

choose a single frame from this set to represent the

fronto-parallel region. In (Efros et al., 2004), this

was done using a graph theory approach by running

a shortest path algorithm. We take a somewhat sim-

ilar approach, computing the distances between all

the frames via normalized cross-correlation then ﬁnd-

ing the frame whose distance is the closest to all the

others. This is equivalent to ﬁnding the frame clos-

est to the mean of this reduced set of frames. We

then mosaic all sub-regions and use a blending algo-

rithm (Szeliski and Shum, 1997) to produce the ﬁnal

reconstructed image.

(a) (b) (c)

(d) (e) (f)

Figure 4: (a) S ubregions being compared. (b) Mean of

the 4 resulting clusters, (c) frames belonging to the chosen

sharpest cluster, (d) frames remaining after removing those

with lower high frequency values, (e) ﬁnal frame choice to

represent subregion, (f) and average over all frames (shown

for comparison).

Figure 4 illustrates the steps for ﬁnding the best

frame of each set. The algorithm takes the frames in

each subregion (Figure 4a) and use K-Means to pro-

duce four clusters (Figure 4b). After variance calcu-

lations, the algorithm determined the top-left cluster

of Figure 4b to be the one with the least overall dis-

tortion. The images in this cluster are then ranked in

decreasing order of high-frequency energy and those

frames whose energy is lower than the mean are re-

moved in an attempt to further reduce the dataset. The

remaining frames are shown in Figure 4d. From this

reduced set, normalized cross correlation distances

are computed in an attempt to ﬁnd the best choice.

Figure 4e shows the output, and Figure 4f shows the

temporal average of the region for comparison.

5 EXPERIMENTS

In this section we present experimental results for

video sequences recorded in the laboratory and in nat-

ural environments. Current experiments show very

promising results.

In the ﬁrst experiment, we analyze an 80-frame

video sequence (Figure 1). The waves in this data

set were low energy waves, large enough to cause a

considerable amount of distortion, yet small enough

not to cause any signiﬁcant separation or occlusion of

the submerged object. The level of distortion in this

dataset is similar to the one used in (Murase, 1992).

Our method provides much sharper results when com-

pared to simple temporal averaging. We extracted

the subregions with 50% overlap. A simple blend-

ing process (Szeliski and Shum, 1997) is applied to

reduce the appearance of “tiles” as observed in the ﬁ-

nal reconstructed image. The results can be seen in

Figure 5. As expected, the blending process slightly

reduced the sharpness of the image in some cases due

to the fact that it is a weighted averaging function.

Figure 5: Low-energy wave dataset. (a) Average over all

frames. (b) Output using our method.

The next experiment shows the output of the algo-

rithm when the input video sequence contains waves

of high energy. These waves may occlude or sepa-

rate the underwater object at times, temporarily mak-

ing subregions completely blurry and unrecognizable.

IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES

233

Figure 6: High-energy wave dataset. (a) Average over all

frames. (b) Output using our method.

For a few regions of the image, the dataset does not

contain a single frame in which the object is clearly

observed, making it difﬁcult to choose a good frame

from the set. The blur and occlusion complicate the

reconstruction problem, but our algorithm handles it

well by explicitly measuring blur and using it to se-

lect high-quality frames from each cluster. Figure 6

shows our results.

Our ﬁnal experiments deal with datasets obtained

in a natural outdoor environment. The videos were

acquired from the moving stream of a small creek.

The waves in this dataset are of high energy, but un-

like the previous dataset, these are of low magnitude

but very high frequency and speed, naturally gener-

ated by the creek’s stream. Figures 7 and 8 show our

results.

6 CONCLUSIONS

We propose a new method for recovering images of

underwater objects distorted by surface waves. Our

method provides promising improved results over

computing a simple temporal average. It begins by di-

viding the video frames into subregions followed by a

temporal comparison of each region, ﬁltering out the

low distortion frames via the K-Means algorithm and

frequency domain analysis of motion blur.

In our method, we approach the problem in a way

similar to (Efros et al., 2004) as we perform a tempo-

ral comparison of subregions to estimate the center of

the Gaussian-like distribution of an ensemble of local

subregions. Our approach differs from theirs in two

main aspects. First, we considerably reduce the “leak-

age” problem (i.e., erroneous NCC correlations being

Figure 7: Creek stream data set 1. (a) Average over all

frames. (b) Output using our method.

classiﬁed as shortest distances) by clustering the sub-

regions using a multi-stage approach that reduces the

data to a small number of high-quality regions. Sec-

ond, we use frequency-domain analysis that allows us

to quantify the level of distortion caused by motion

blur in the local sub-regions. Our results show that

the proposed method is effective in removing distor-

tion caused by refraction in situations when the sur-

face of the water is being disturbed by waves. A di-

rect comparison between our method and previously

published methods (Efros et al., 2004; Murase, 1992;

Shefer et al., 2001) is difﬁcult due to the varying wave

conditions between data sets, as well as the lack of

a method for quantifying the accuracy of the recon-

struction results.

Working with video sequences that contain high

energy waves is a complex task due to occlusion and

blurriness introduced into the image frames. Our al-

gorithm handles these conditions well by explicitly

measuring blur in each subregion. Additionally, large

energy waves introduce the problem that a given em-

bedding of subregions may not contain a single frame

corresponding, or near, to a point in time when the

VISAPP 2006 - IMAGE ANALYSIS

234

Figure 8: Creek stream data set 2. (a) Average over all

frames. (b) Output using our method.

water normal is parallel to the camera’s optical axis.

This affects the quality of our results.

Our plans for future research involve extending the

current algorithm to improve results when dealing

with high energy waves. We are currently researching

the incorporation of constraints provided by neigh-

boring patches. These constraints can, in principle,

be added by means of global alignment algorithms.

Further lines of research involve extending the cur-

rent method to use explicit models of both waves and

refraction in shallow water (Gamito and Musgrave,

2002), and the application of our ideas to the problem

of recognizing submerged objects and textures. We

are currently working on developing these ideas and

they will be reported in due course.

ACKNOWLEDGMENTS

The authors would like to thank Dr. Alexey Efros

for kindly providing us with an underwater video se-

quence which we used to initially develop and test our

algorithm.

REFERENCES

Cox, C. and Munk, W. (1956). Slopes of the sea surface

deduced from photographs of the sun glitter. Bull.

Scripps Inst. Oceanogr., 6:401–488.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern

Classiﬁcation (2nd Edition). Wiley-Interscience.

Efros, A., Isler, V., Shi, J., and Visontai, M. (2004). See-

ing through water. In Saul, L. K., Weiss, Y., and

Bottou, L., editors, Advances in Neural Info rmation

Processing Systems 17, pages 393–400. MIT Press,

Cambridge, MA.

Field, D. and Brady, N. (1997). Visual sensitivity, blur and

the sources of variability in the amplitude spectra of

natural scenes. Vision Research. Dec;37(23):3367-

83., 37(23):3367–3383.

Gamito, M. N. and Musgrave, F. K. (2002). An accurate

model of wave refraction over shallow water. Com-

puters & Graphics, 26(2):291–307.

Gonzalez, R. C. and Woods, R. E. (1992). Digital Image

Processing. Addison-Wesley, Reading, MA.

Mall, H. B. and da Vitoria Lobo, N. (1995). Determining

wet surfaces from dry. In ICCV, pages 963–968.

Murase, H. (1992). Surface shape reconstruction of a non-

rigid transparent object using refraction and motion.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 10(10):1045–1052.

Premoze, S. and Ashikhmin, M. (2001). Rendering natural

waters. Computer Graphics Forum, 20(4).

Shefer, R., Malhi, M., and Shenhar, A. (2001).

Waves distortion correction using cross corre-

lation. (http://visl.technion.ac.il/projects/2000maor/).

http://visl.technion.ac.il/projects/2000maor/.

Szeliski, R. and Shum, H.-Y. (1997). Creating full view

panoramic image mosaics and environment maps. In

SIGGRAPH ’97: Proceedings of the 24th annual con-

ference on Computer graphics and interactive tech-

niques, pages 251–258, New York, NY, USA. ACM

Press/Addison-Wesley Publishing Co.

Walker, R. E. (1994). Marine Light Field Statistics. John

Wiley & Sons.

Wang, Z. and Simoncelli, E. P. (2004). Local phase coher-

ence and the perception of blur. In Thrun, S., Saul,

L., and Sch

olkopf, B., editors, Advances in Neural In-

formation Processing Systems 16. MIT Press, Cam-

bridge, MA.

Young, I. R. (1999). Wind Generated Ocean Waves. Else-

vier.

IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES

235