VISION-BASED TRACKING SYSTEM FOR HEAD MOTION

CORRECTION IN FMRI IMAGES

Tali Lerner and Ehud Rivlin

Department of Computer Science, Technion-Israel Institute of Technology, Haifa 32000, Israel

Moshe Gur

Department of Biomedical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel

Keywords:

fMRI, pose estimation, motion correction, tracking.

Abstract:

This paper presents a new vision-based system for motion correction in functional-MRI experiments. fMRI

is a popular technique for studying brain functionality by utilizing MRI technology. In an fMRI experiment

a subject is required to perform a task while his brain is scanned by an MRI scanner. In order to achieve

a high quality analysis the fMRI slices should be aligned. Hence, the subject is requested to avoid head

movements during the entire experiment. However, due to the long duration of such experiments head motion

is practically unavoidable. Most of the previous work in this ﬁeld addresses this problem by extracting the

head motion parameters from the acquired MRI data. Therefore, these works are limited to relatively small

movements and may confuse head motion with brain activities. In the present work the head movements

are detected by a system comprised of two cameras that monitor a specially designed device worn on the

subject’s head. The system does not depend on the acquired MRI data and therefore can overcome large head

movements. Additionally, the system can be extended to cope with inter-block motion and can be integrated

into the MRI scanner for real-time updates of the scan-planes. The performance of the proposed system was

tested in a laboratory environment and in fMRI experiments. It was found that high accuracy is obtained even

when facing large head movements.

1 INTRODUCTION

Magnetic Resonance Imaging (MRI) technology

plays a central part in human brain research in the

last decade (Belliveau et al., 1991; Bandettini et al.,

1992). The utilization of MRI for brain functional-

ity studies is referred to as functional MRI (fMRI).

In fMRI studies a subject is requested to perform a

task while his brain is repeatedly scanned. These

tasks may include viewing images, listening to dif-

ferent sounds, performing a mathematical calculation

and others. Statistical techniques are applied on the

acquired fMRI scans in order to analyze the func-

tionality of the examined parts in the subject’s brain.

The duration of an fMRI experiment may be rela-

tively long (tens of minutes). During this time the

subject is requested to avoid head movements in order

to acquire aligning MRI scans along the experiment.

The subject’s head is stabilized (with pads) to prevent

large head movements. However, small perturbations

and slow drift of the head position are practically un-

avoidable. These motions deteriorate the alignment of

scans that were acquired at different time instances,

and therefore reduce the credibility and the accuracy

of the statistical analysis (see Fig. 1). It is desirable

to correct these displacement effects in the MRI slices

before analyzing them.

The problem of motion correction in fMRI slices

is discussed in several previous studies. Most stud-

ies derive the motion parameters from the acquired

slices using different methods. These image-based

techniques tend to fail in the presence of relatively

large displacement. Additionally, due to brain activ-

ities, the gray levels of the image vary and may be

confused with the head motion effects leading to a re-

duction in the accuracy of the motion estimates. Some

of these studies handle 2D displacement in each slice

separately and overlook the 3D nature of the head

movement. Other studies extract the 3D motion pa-

rameters from the MRI slices under the assumption

that no motion had occurred during the block (a set

of subsequent MRI slices) acquisition but rather only

between the different blocks.

The most traditional approach for ﬁnding the mo-

tion parameters is to compute the 2D transformation

which best aligns a shifted image with a reference im-

213

Lerner T., Rivlin E. and Gur M. (2006).

VISION-BASED TRACKING SYSTEM FOR HEAD MOTION CORRECTION IN FMRI IMAGES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 213-220

DOI: 10.5220/0001370202130220

 SciTePress

Figure 1: Illustration of the slice misalignment caused by

the head motion. The acquired slices after the motion do

not align with the original slices.

age. The alignment techniques can be classiﬁed into

two groups: image intensity based and Fourier space

based. The image intensity based group includes the

works (Woods et al., 1992; Woods et al., 1993) which

suggest deﬁning images as being effectively the same

when their voxel-by-voxel ratio is a constant. (Haj-

nal et al., 1995) suggests deﬁning the difference be-

tween images using the mean square voxel-by-voxel

error. Other intensity based works can be found in

(Friston et al., 1996; Thesen et al., 2000; Ciulla and

Deek, 2002). The Fourier space alignment techniques

detect the motion parameters using Fourier methods

that can be applied on the raw data of MRI images

since it is collected in that domain. Examples of such

techniques can be found in (Zorooﬁ et al., 1996; Kim

et al., 2002; Caparelli et al., 2003). A different ap-

proach can be found in (Derbyshire et al., 1998). The

described real-time system extracts the 3D position of

the subject’s head from an external source of informa-

tion. Three coils are attached to the subject’s head and

their spacial location is monitored using magnetic res-

onance techniques. The computed motion is applied

on the MRI scan-plane in order to chase the subject’s

head. The disadvantage of this system is the limited

number of features (the coils) that lead to poor esti-

mation of head position.

In the present work a new vision-based solution to

the head motion correction problem is presented. The

proposed system includes two calibrated and synchro-

nized cameras for tracking the movements of a spe-

cially designed device which is worn on the subject’s

head. The monitored motion is utilized to produce

motion-free MRI slices. Similarly to (Derbyshire

et al., 1998) the system computes the 3D motion pa-

rameters using an external source of information (the

optical tracking conﬁguration), and therefore it can

overcome extremely large head motion. Although the

Figure 2: The system conﬁguration. The subject is wear-

ing the device on his head and the two cameras monitor the

movements of the tracking device.

system presented here assumes no head motion dur-

ing the block acquisition it can be easily extended to

cope with inter-block motion when detecting the head

position for each slice separately.

The rest of this paper is organized as follows: Sec-

tion 2 gives a brief overview of the system. Section

3 describes the algorithms and devices used for the

system calibration. The algorithms and devices used

for the motion detection are described in Section 4.

A method for correcting the MRI data is presented in

Section 5. Section 6 elaborates on a series of lab ex-

periments and Section 7 shows qualitative and quanti-

tative results when applying the system in a real fMRI

experiment. Finally, conclusions are noted in Section

2 SYSTEM OVERVIEW

The system presented in this work is composed of a

specially designed tracking device which is strapped

to the subject’s head, and two cameras with zooming

capability. The cameras are positioned on both sides

of the MRI bed and monitor the movements of the

tracking device (see Fig. 2). When using the system,

three main stages are performed: system calibration,

head motion detection, and MRI blocks correction.

In the system calibration stage, the internal para-

meters of the two cameras and their relative position

are computed. Once this information is evaluated the

pose (position + orientation) of the subject’s head w.r.t

the cameras’ coordinate systems can be accurately de-

tected using stereopsis methods. Since the ﬁnal objec-

tive is to correct the motion in the MRI slices, the head

motion w.r.t the MRI system is required. For that aim

the pose of the cameras w.r.t the MRI system is also

extracted during the calibration phase.

Once the system is calibrated the fMRI experiment

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

214

Figure 3: The calibration device designed for computing the

relative position of the cameras.

can begin. A head device is strapped to the subject’s

head during the experiment. Due to rigid body motion

laws a single motion transformation applies to both

the head and the head device. Therefore, by monitor-

ing the pose of the head device the head movements

can be deduced. Using the cameras relative position

w.r.t the MRI, the head motion transformation can be

expressed under the MRI coordinate system.

Finally, the MRI blocks can be corrected. Utiliz-

ing the head motion transformation, a compensating

transformation can be applied on the MRI blocks.

The generated motion-free blocks are the blocks that

would have been obtained in the absence of head mo-

tion.

3 SYSTEM CALIBRATION

The calibration procedure starts by obtaining the in-

ternal parameters of each camera using a standard

technique (Bouguet, ). Next, the relative pose be-

tween the two cameras and their pose w.r.t the MRI

system are estimated. The rest of this section elab-

orates on the methods and the custom made devices

that participate in these procedures.

3.1 Finding the Cameras Relative

Position

Extremely accurate pose estimates are required for

a qualitative motion correction of the fMRI slices.

For this purpose, a multi-camera pose estimation al-

gorithm, referred to as TwoCamPose, is presented in

Section 4.2. This algorithm requires the relative posi-

tion and orientation between the two cameras. The ac-

curacy of this connecting transformation signiﬁcantly

inﬂuences the obtained accuracies of the TwoCam-

Pose algorithm. A calibration device composed of

three planes is designed. Two planes create an an-

gle of 120

◦

and the third plane is orthogonal to both

of them. On each plane a chessboard image was at-

tached (see Fig. 3). The 3D locations of the corners

on the three chessboards are known and serve as fea-

tures for the device pose computation. The fact that

(a) (b)

Figure 4: The phantom device designed for linking the cam-

eras to the MRI coordinate system.

the features constellation is not coplanar drastically

improves the accuracy of the obtained pose estimates.

The device is placed in several positions and its poses

w.r.t each of the cameras are computed. The connect-

ing transformation between the cameras is computed

as the composition of the device poses:

cam2

cam1

T =

cam2

device

T ·

device

cam1

T (1)

where

T represents the Euclidean transformation

from coordinate system A to B. The parameters of

these composed transformations are averaged to de-

rive the ﬁnal estimate of the cameras relative position

and orientation.

3.2 Cameras Pose w.r.t the MRI

Coordinate System

Although the cameras’ relative position enables the

computation of the tracking device pose w.r.t the cam-

eras, the required information is its motion w.r.t the

MRI coordinate system. Therefore, the linking trans-

formation from the cameras coordinate system to the

MRI coordinate system is necessary. For this purpose

a device, referred to as phantom, is designed (see Fig.

4(b)). This device is composed of two main com-

ponents. At the front end a planar chessboard is in-

stalled. Using the TwoCamPose algorithm the pose

of the phantom device is obtained. At the back end,

a 120 × 120 × 50 mm water container is attached

see Fig. 4(a). This container is scanned by the MRI

scanner using high resolution parameters. Next, the

slices produced by the MRI scanner are registered to

the geometrical model of the container. In order to

acquire the 3D registration parameters with high ac-

curacy, sixteen stakes were added to the geometrical

structure of the container. Once the poses of the phan-

tom w.r.t the MRI system and the cameras are known,

the linking transformation between the cameras and

the MRI system is derived.

VISION-BASED TRACKING SYSTEM FOR HEAD MOTION CORRECTION IN FMRI IMAGES

215

Figure 5: The head device strapped to a subject’s head.

4 MOTION DETECTION

This section details the heart of the system that is pre-

sented in this paper. The detection of the subject’s

head motion is performed throughout the entire fMRI

experiment. A specially designed device is strapped

to the subject’s head and is monitored by the two cam-

eras. Later, the recorded information is analyzed in

order to compute the compensating transformations

for the MRI slices.

4.1 The Head Device

Monitoring the head movements is performed using a

device that is worn by the subject. The device is com-

posed of a strip which is placed on the subject’s head,

and two rods attached to it from both sides of the head

near his temples. These rods are linked together in

front of the chin to a tracking device that is monitored

by the cameras (see Fig. 5). The tracking device is

built of two 50× 80 mm planes that create an angle of

◦

between them. “L”-shaped features are arranged

in four rows on the tracking device planes. The fea-

tures in each row have a unique orientation which as-

sist in the correspondence solution. The features ori-

entation is detected by examining the direction of the

vector from the center of the L-feature bounding-box

to its gravity-center (see Fig. 6). The described con-

ﬁguration of the tracking device enables obtaining the

head motion with high accuracy, as can be observed

in Section 6.

4.2 The “TwoCamPose” Algorithm

During the system calibration procedure the relative

position of the two cameras is computed. Utilizing

this piece of information, the pose of the tracking

device can be obtained in a straightforward manner:

ﬁrst, the 3D location of each feature is separately

(a) (b) (c) (d)

Figure 6: Orientation classiﬁcation method of the L-shaped

features on the tracking device. The cyan dot represents the

center of the feature’s bounding box while the purple dot

represents its center of gravity. The classiﬁcation method

utilizes the direction of the green arrows shown in (a)-(d).

reconstructed w.r.t the cameras using a standard tri-

angulation algorithm (Hartley and Zisserman, 2000).

Next, the pose is computed from the 3D-to-3D fea-

ture registration (Umeyama, 1991). This approach

is advantageous because both steps have closed-form

solutions which make them computationally attrac-

tive. However, the triangulation step of the above ap-

proach overlooks the known 3D constellation of the

features. Since the pose estimation computation is

performed off-line, obtaining high accuracy is pre-

ferred over computational duration. Hence, an alter-

native method for the pose computation, referred to

as “TwoCamPose”, is proposed. Let p

be the 3D lo-

cation of the i’th feature w.r.t the coordinate system

of the model. Let t

and R

be the relative position

and orientation, respectively, between the two cam-

eras. Given the 2D measurements from each of the

cameras -

i,1

and

i,2

, this algorithm searches for the

pose that minimizes the objective-function:



i=1



)

−

i,1





+ t

)

−

i,2



(2)

where v

= R · p

+ t, R and t are the pose hy-

pothesis. The above function reﬂects the sum of the

squared distances between the 2D extracted features

from each camera and their reprojected 3D features

given a pose hypothesis. This function was mini-

mized using the Newton-Raphson optimization tech-

nique. Although the TwoCamPose algorithm is pre-

sented for only two cameras it can be easily extended

to an arbitrary number of cameras. The TwoCamPose

algorithm achieves more accurate pose estimates than

the triangulation technique as will be shown in Sec-

tion 6.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

216

4.3 Construction of the

Compensating Transformation

By composing two poses of the tracking device w.r.t

the cameras, the device’s motion, and thus the sub-

ject’s head motion, is computed. Therefore, this mo-

tion transformation is also obtained w.r.t the cameras.

Since the fMRI slices are acquired w.r.t the MRI sys-

tem, the motion transformation must be expressed

w.r.t the same system. Consider two time instances:

and t

, before and after a single movement of the

head. Each time instance corresponds to a coordinate

system D

and D

attached to the tracking device.

Consider a point p

in the subject’s brain. Due to the

head movement this point is transferred to a new po-

sition p

. Since it is assumed that the tracking device

and the head move rigidly:

. (3)

In the above equation the left superscript describes

the coordinate system in which the vector is repre-

sented. Let

T be the desired transformation between

the points p

and p

under the MRI coordinate sys-

tem. Using this transformation one can write:

MRI

T ·

MRI

. (4)

The positions of p

and p

in the MRI system are

given by

MRI

T ·

(5)

where i =1, 2. Assigning Equation (5) to both sides

of Equation (4) yields:

MRI

T ·

MRI

T ·

. (6)

Multiplying the left side of (6) by

MRI

T results:

MRI

T ·

MRI

T ·

. (7)

Recalling (3), the multiplication of the three transfor-

mations must be the identity transformation I:

MRI

T ·

MRI

T = I. (8)

Multiplying by the inverse transformations yields the

ﬁnal result:

T =

MRI

T ·

MRI

T. (9)

This transformation supplies a description of the sub-

ject’s head motion between two time instances during

the fMRI experiment.

In this work the ﬁrst block is perceived as the ref-

erence block while the rest of the blocks are corrected

according to its position. As a result, the movements

between the reference block and the rest of the blocks

w.r.t the MRI coordinate system are computed as de-

scribed above. Similarly to (Derbyshire et al., 1998)

the

T transformation could be supplied to the MRI

scanner in order to update the scan-planes position.

This way the slices chase the subject’s head position

during their acquisition and therefore no postprocess-

ing motion compensation is necessary.

Figure 7: Motion compensation in the fMRI slices. The

head movement transformation –

T is applied to each of the

MRI slices’ grid points.

5 MOTION COMPENSATION IN

MRI SLICES

The motion compensation is the ﬁnal step of the sys-

tem presented in this work. In this step, motion-free

slices are synthesized from the existing MRI slices us-

ing the head movement transformation -

T . As men-

tioned above, a single transformation is assigned to

each block in the fMRI data. By applying this trans-

formation on the block, its slices chase the subject’s

moving head. Each slice is represented by a 3D regu-

lar and planar grid. The grid points represent the cen-

ter of voxels in the MRI scan. The location of the grid

points w.r.t the MRI coordinate system is supplied

by the MRI image format. In order to produce the

motion-free slice, the

T transformation is applied on

each of the grid points (see Fig. 7). The new gray level

of the transformed grid point is determined by identi-

fying its eight surrounding voxels in the origin block

and applying trilinear interpolation on their gray level

values.

6 LAB EXPERIMENTS

A series of lab experiments were conducted to eval-

uate the ability of the TwoCamPose algorithm de-

scribed in section 4.2 to detect small motions and

compare its accuracy to the triangulation based 3D

reconstruction algorithm described in the same sec-

tion. The tracking device was attached to a robotic

arm and small motion was applied to it. The ex-

periment involved moving the tracking device along

VISION-BASED TRACKING SYSTEM FOR HEAD MOTION CORRECTION IN FMRI IMAGES

217

a constant direction by ten steps of 0.1 mm in or-

der to complete a trajectory of 1 mm. The motion

was translational only, no rotation was involved. The

eleven poses were estimated using the two evaluated

algorithms. Although the structure of the true tra-

jectory was known (pure translational motion along a

constant direction), its relative position w.r.t the cam-

eras was unknown. In order to overcome this obsta-

cle, least squares alignment was performed between

the true trajectory and the measured trajectory (the

eleven poses), and the distances between the two ﬁt-

ted trajectories were measured. Three different trajec-

tories were examined. Each one aligned with one of

the main axes: X, Y, and Z. Tables 1 and 2 compare

the mean and maximal errors of the two evaluated al-

gorithms computed from the three trajectories. One

can easily observe that the TwoCamPose algorithm

achieves better results. The results of the experiment

indicate that motions as small as 0.1 mm can be de-

tected with high accuracy using the TwoCamPose al-

gorithm. These accuracies are very small compared

to the fMRI image resolution which is at least 1.75

mm in X and Y axes and 2.8 mm in the Z axis.

7 RESULTS

In this section the results that were obtained by the

system described in this work are presented. fMRI

experiments with a subject were conducted. The sub-

ject wore the head device and visual stimulations were

presented to him while his brain was scanned (see Fig.

2 for the experiment’s setup). Three experiments were

recorded. In the ﬁrst one the subject was asked to

avoid motion as much as possible, in the second ex-

periment the subject was asked to move slightly; and

in the last experiment the subject was allowed to per-

form larger movements.

The algorithms described in this work were applied

on the recorded MRI blocks producing new motion-

free blocks. These corrected blocks were compared

to the original (uncorrected) blocks both qualitatively

and quantitatively. Figures 8 through 10 show an ex-

ample of the displacement and the correction quality

of a single slice. In each ﬁgure, the blue line repre-

sents the contour of the brain in the ﬁrst block, the red

dashed line represents the contour of the brain taken

from another block, and the green dashed line rep-

resents the contour of the brain taken from the same

block after compensation. As can be observed, the

brain offset was correctly detected and compensated

even in cases of large head motion. In Fig. 11 the

average image of the corresponding slices taken from

all the original blocks is compared to the same one

taken from the corrected blocks. As can be observed,

the average image of the original blocks is blurred and

Figure 8: Motion compensation in a slice from the ﬁrst ex-

periment (no intended motion).

unclear while these artifacts are signiﬁcantly reduced

in its corrected counterpart.

In addition to the described qualitative results, a

quantitative comparison between the original and the

corrected blocks from the three experiments is pre-

sented in Table 3. Two measurements were used for

this comparison: correlation coefﬁcient and Forbe-

nius norm. The correlation coefﬁcient is computed

by:

c =



−

R)(A

−



(



−

)(



−

)

(10)

where A is a slice and R is its corresponding reference

slice.

R and

A are the mean values of the these slices.

The Forbenius norm value is deﬁned as:

f =





− A

)

. (11)

For both measurements the ﬁrst block served as a

reference block. The similarity between each slice

and its corresponding slice in the reference block was

evaluated by the two measurements. The similarity of

the entire experiment was evaluated by averaging the

similarity measurement of all its slices. As shown in

Table 3 the alignment quality of the original blocks

deteriorates when the motion’s magnitude increases.

The corrected blocks, on the other hand, maintain

high and almost constant alignment quality for all mo-

tion types. These results verify the advantage of uti-

lizing the proposed system in fMRI experiments.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

218

Table 1: Comparison of the translation errors in each trajectory between the TwoCamPose and the Triangulation algorithms

described in Section 4.2. The translation error is measured in mm.

Alg. X Y Z

Mean Max Mean Max Mean Max

TwoCamPose 0.0204 0.0335 0.0277 0.0721 0.0283 0.0559

Triangulation 0.0651 0.1308 0.0719 0.186 0.0602 0.1055

Table 2: Comparison of the rotation errors in each trajectory between the TwoCamPose and the Triangulation algorithms

described in Section 4.2. The angular error is measured in degrees.

Alg. φ θ ψ

Mean Max Mean Max Mean Max

TwoCamPose 0.0131 0.0197 0.0117 0.017 0.0115 0.0162

Triangulation 0.0801 0.1734 0.0619 0.1418 0.0736 0.1195

(a) (b) (c)

Figure 11: Average images comparison of the third experiment (relatively large intended motion). (a) a slice from the ﬁrst

(reference) block. (b) the average image of the corresponding slices from all the original blocks. (c) the average image of the

corresponding slices from all the corrected blocks.

Table 3: In this table the original and corrected blocks are compared by the average correlation coefﬁcient (Equation 10) and

average Forbenius norm (Equation 11) which were obtained from the three experiments.

Small Motion Medium Motion Large Motion

Correlation Forbenius Correlation Forbenius Correlation Forbenius

Original 0.9865 6.1136 0.9816 7.3265 0.9411 13.569

Corrected 0.9963 3.8939 0.9957 3.8394 0.9946 4.3644

8 CONCLUSIONS

In this paper a new vision-based system for motion

correction in fMRI experiments is proposed. The

quality of the experiment’s analysis signiﬁcantly de-

pends on the magnitude of the subject’s head move-

ments while the MRI scans were acquired. Due to

the typical long duration of an fMRI experiment, head

motion is practically unavoidable. Most of the previ-

ous work in this ﬁeld addressed this problem by ex-

tracting the head motion parameters from the acquired

MRI data. The system that was presented here de-

tects the head movements using two calibrated cam-

eras that monitor a head-device worn by the subject

during the experiment. The system does not depend

on the acquired MRI data and therefore can overcome

large head movements. Additionally, the system can

be extended to cope with inter-block motion and can

be integrated into the MRI scanner for real-time up-

dates of the scan-planes. As was shown in the lab

experiments, the head motion is detected with sub-

millimetric accuracy. The applicability of the system

was tested with subjects and proved to achieve a high

quality correction of corrupted MRI data even when

dealing with large head motion.

VISION-BASED TRACKING SYSTEM FOR HEAD MOTION CORRECTION IN FMRI IMAGES

219

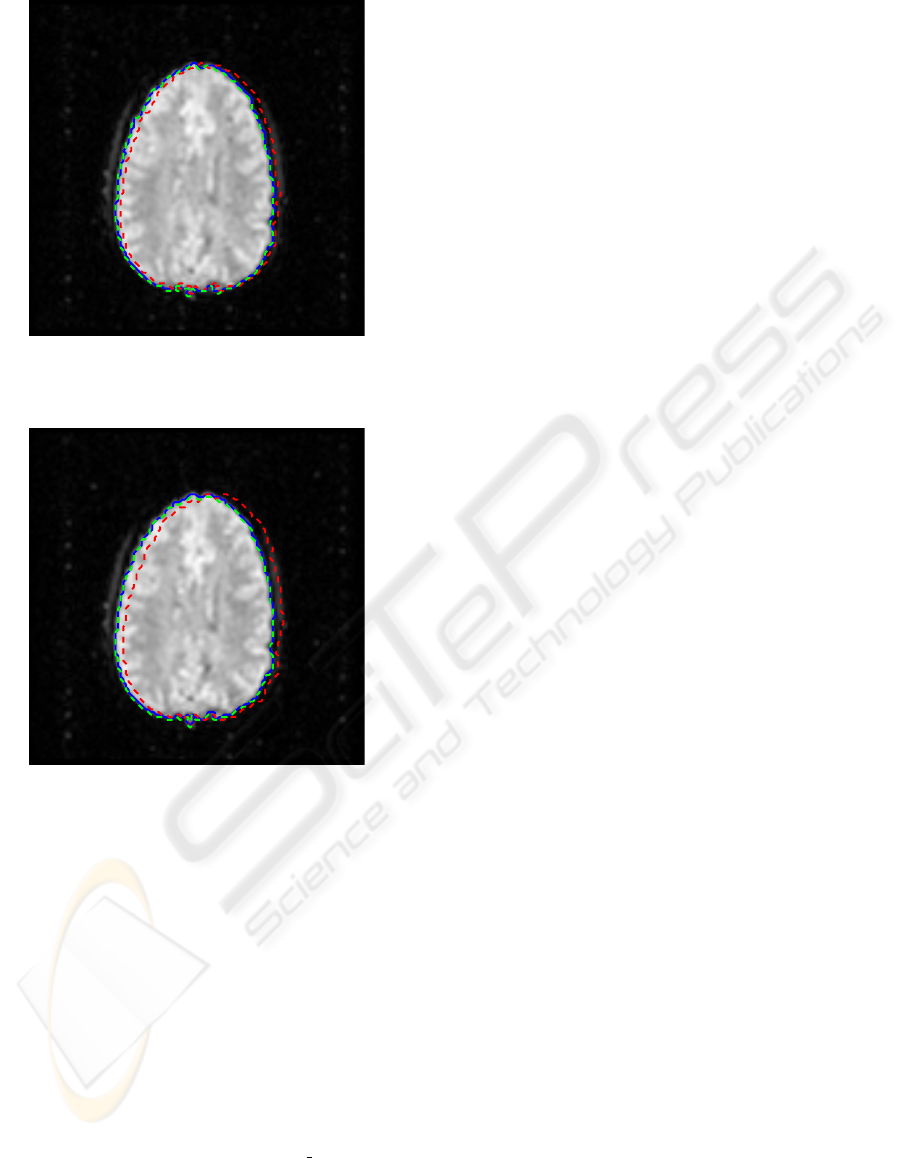
Figure 9: Motion compensation in a slice from the second

experiment (small intended motion).

Figure 10: Motion compensation in a slice from the third

experiment (relatively large intended motion).

REFERENCES

Bandettini, P., Wong, E., Hinks, R., Tikofsky, R., and Hyde,

J. (1992). Time course epi of human brain function

during task activation. Journal of Magn. Reson. Med.,

25:390–397.

Belliveau, J., Kennedy, D., McKinstry, R., Buchbinder, B.,

Weisskoff, R., Cohen, M., Vevea, J., Brady, T., and

Rosen, B. (1991). Functional mapping of the human

visual cortex by magnetic resonance imaging. Sci-

ence, 254:716–719.

Bouguet, J. Camera calibration toolbox for matlab.

www.vision.caltech.edu/bouguetj/calib

doc.

Caparelli, E., Tomasi, D., Arnold, S., Chang, L., and Ernst,

T. (2003). K-spaced based summary motion detection

for functional magnetic resonance imaging. NeuroIm-

age, 20:1411–1418.

Ciulla, C. and Deek, F. (2002). Performance assessment

of an algorithm for the alignment of fmri time series.

Brain Tomography, 14:NO. 4.

Derbyshire, J., Wright, G., Henkelman, R., and Hinks, R.

(1998). Dynamic scan-plane tracking using mr po-

sition monitoring. Journal of Magn. Reson. Med.,

5:924–932.

Friston, K., William, S., Howard, R., Frackowiak, R., and

Tuner, R. (1996). Movement-related effects in fmri

time-series. Journal of Magn. Reson. Med., 35:346–

355.

Hajnal, J., Saeed, N., Soar, E., Oatridge, A., Young, I., and

Bydder, G. (1995). A registration and interpolation

procedure for subvoxel matching of serially acquired

mr images. Journal of Computer Assisted Tomogra-

phy, 19:289–296.

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision. Cambridge University Press,

Cambridge.

Kim, E., Park, N., Choi, M., and Tamura, S. (2002). Cancel-

lation of mri motion artifact in image plane. In IEEE

Intrumentation and Measurements.

Thesen, S., Hied, O., Mueller, E., and Schad, L. (2000).

Prospective acquisition correction for head tracking

for real-time fmri. Journal of Magn. Reson. Med.,

44:457–465.

Umeyama, S. (1991). Least-squares estimation of transfor-

mation parameters between two point patterns. IEEE

Trans. on Pattern Analysis and Machine Intelligence,

13,Journal of Computer Assisted Tomography:376–

380.

Woods, R., Cherry, S., and Mazziotta, J. (1992). Rapid auto-

mated algorithm for aligning and reslicing pet images.

Journal of Computer Assisted Tomography, 16:620–

633.

Woods, R., Mazziotta, J., and Cherry, S. (1993). Mri-

pet registration with automated algorithm. Journal of

Computer Assisted Tomography, 17:536–546.

Zorooﬁ, R., Sato, Y., S.Tamura, and Naito, H. (1996). Mri

artifacts cancellation due to rigid motion in the imag-

ing plane. IEEE Tran. on Medical Imaging, 15:NO.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

220