COMPARING YEAST CELLS SEGMENTATION THROUGH

HIERARCHICAL TREES

Marco Antonio Garcia de Carvalho

Universidade Estadual de Campinas - UNICAMP

Rua Paschoal Marmo, 1888, Jd. Nova Itlia, 13484-370, Limeira/SP - Brazil

Tiago Willian Pinto

Universidade Estadual de Campinas - UNICAMP

Rua Paschoal Marmo, 1888, Jd. Nova Itlia, 13484-370, Limeira/SP - Brazil

Keywords:

Image segmentation, Hierarchical analysis, yeast cells, Mathematical Morphology, tree representation.

Abstract:

Image ﬁltering and segmentation consists of se parating an image into regions according to some criteria and

to the application ﬁnality. Recent publications in the image processing domain make use of a segmentation

strategy called multiscale or hierarchical segmentation. The multiscale segmentation provides a family of

partitions of an image, presenting it at several levels of resolution. This work studies a multiscale image

representation called Tree of the Critical Lakes (TCL), that provides an set of nested partitions of an image.

The Tree of the Critical Lakes is deﬁned from the Watershed Transform, the traditional tool of Mathematical

Morphology in image segmentation operations. Moreover, we implement a comparison between TCL and

another way of image representation, called Component Tree (CT). The CT consists of a set of cross-sections

images and its connected components, linked thanks to the inclusion relation. We show experiments of image

segmentation, based on TCLs and CTs, for a group of yeast cells images.

1 INTRODUCTION

Recent segmentation methods tend to consider the

hierarchical structure of images in object oriented

analysis, segmentation and coding. A hierarchy al-

lows the utilization of both the superﬁcial and the

deep image structure (set of possible regions and con-

tours).

In this work we exploit two graph structures know

as Tree of Critical Lakes (TCL) and Component Tree

(CT) in order to implement yeast image segmentation.

The Watershed Transform is used to build the TCL

which provides a set of nested partitions of the image.

Yeast characterization by image analysis methods

(O´Shea and Walsh, 2000)-(Pons et al., 1993) has

been developed aiming at segmenting and classify-

ing cells in an automatic or semi-automatic way. The

knowledge of yeast features is important to several

chemical processes. We exploit geometric and hier-

archical properties of all nodes of the Tree of Critical

Lakes, such as survival time, ellipse ﬁtting criterion

and region attributes, in order to discriminate yeast

cells(Carvalho, 2004).

On the other hand, we implemented comparisons

with the Component Tree. The CT is a structure

builded from the thresholding process of an image,

that consists of computing the cross-sections of an im-

age, for each grey level. In the following, the link

between connected components at each cross-section

is stablished. Several authors have used this repre-

sentation to implement some morphological operators

(Najman and Couprie, 2004), image ﬁltering (Jonnes,

1997) and image matching (Mattes et al., 1999).

The paper is organized as follows. First, we show

in Section 2 some graphs concepts and deﬁnitions.

Section 3 presents how we create a scale-space rep-

resented by the Tree of Critical Lakes. Section 4 is

devoted to present the Component Tree and the image

ﬁltering process. Experimental results of the yeast

segmentation by TCL and CT were compared and are

shown in Section 5. Finally, the conclusions and fu-

ture works are presented in 6.

2 GRAPH DEFINITION

Let G = (V, E) be a non-directed graph where V is

the set of nodes or vertices and E is the set of edges

(i, j), for i, j ∈ V . A weighted graph is a graph where

a number (weight) is associated to each edge (i, j),

represented by w (i, j). A path from i

to i

is a list

, i

, . . . i

n−1

, i

) where i

∼ i

k+1

, k = 1, . . . , n-1.

Two nodes i and j are connected if there is at least one

515

Antonio Garcia de Carvalho M. and Willian Pinto T. (2006).

COMPARING YEAST CELLS SEGMENTATION THROUGH HIERARCHICAL TREES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 515-518

DOI: 10.5220/0001371505150518

 SciTePress

path between i and j. A connected graph G is a graph

where all pair of nodes is connected. Let G

be a sub-

graph of G. A connected component CC of G

that

contains one node i is the union of all paths in G

that

originate on i. A tree is a connected graph with no

cycles. A Minimum Spanning Tree (MST) is a tree

that contains all nodes of G and such that the sum of

edge weights is minimal.

3 TCL REPRESENTATION

The classical technique in morphological segmenta-

tion is the Watershed Transform (WT). We summa-

rize in the following the main concepts of watershed.

For a more complete review of watershed variations,

we refer the reader to (Beucher and Meyer, 1993).

3.1 Watershed Transform

We consider the gradient image f as a topographic

surface. An image is segmented by constructing the

catchment basins of its gradient image, as shown in

Figure 1. The gradient image is ﬂooded starting from

selected sources (regional minima) until the whole

image has been ﬂooded. A dam is erected between

lakes that meet with others lakes. At the end of ﬂood-

ing process, we obtain one region for each catchment

basin of the gradient image.

(a) (b)

Figure 1: (a) Original gradient image; the markers are the

regional minima, in gray; the dashed lines separate the wa-

tershed basins. (b) MST of the image (a); the valuation of

the edges corresponds to the volumetric extinction value.

Hierarchical watershed creates a set of nested par-

titions. A partition P of an image f is a set of disjoint

regions R

, i = 1, 2 . . . , n, where the union of re-

gions is the whole image. Let (P

) be a sequence of

partitions P

, P

, . . . , P

, of an image f. (P

) is a hi-

erarchy, also called nested sequence of partitions, if a

partition at a ﬁne level is obtained by merging regions

of the coarse partition.

The watershed problem can be modeled using

graphs. The gradient image is represented by a

weighted neighborhood graph, where: (i) a node rep-

resents a catchment basin of the topographic surface;

(ii) an edge links two nodes if their corresponding

catchment basins are neighbors (in the sense of a pixel

neighborhood); (iii) edge’s weights are given by the

lowest altitude of pass point separating two catch-

ments basins.

The set of all edges (dams) where merging of dif-

ferent original lakes occur constitutes a minimum

spanning tree (MST) of the weighted neighborhood

graph(Meyer and Maragos, 1999). Although the re-

gions merging were controlled by the altitude of topo-

graphic relief, the evaluation of the levels at which

partitions are formed can be performed based on

another value, called the extinction value (Vachier,

1995). We utilize the volumetric extinction value.

Figure 1(b) show the MST of the artiﬁcial image pre-

sented in Figure 1(a).

3.2 Creation of a Scale-space

The TCL is a morphological representation obtained

from Watershed Transform and provides the order of

the fusion regions. Due to its hierarchical properties,

the TCL has the potential to build a family of nested

partitions. The initial partition P

is the labeled image

provided by the Watershed. The other partitions are

formed by agglomerating two-by-two regions (Car-

valho, 2004).

Frequently, the TCL is build from Minimum Span-

ning Tree (MST) of the image. Details of the algo-

rithms concerning the MST and the TCL transforma-

tion can be found in (Meyer and Maragos, 1999) and

(Meyer and Maragos, 1996), respectively.

3.3 Scale-space Analysis

We use some properties of the TCL hierarchical rep-

resentation, in addition to general attributes, in order

to segment yeast cell images. The segmentation al-

gorithm can be summarized by the following 3 steps

(Carvalho, 2004): Scale-space creation; Computa-

tion of attributes; and, Hierarchical analysis (Start the

segmentation analysis by the Survival Time criterion;

after, apply the area criterion to eliminate nodes close

to the TCL root; Finally, apply the other criteria, as

ellipse ﬁtting (Fitzgibbon et al., 1999), region circu-

larity and gray level mean).

4 CT REPRESENTATION

4.1 Deﬁnition

The component tree is a representation of a grayscale

image based on the cross-section decomposition

VISAPP 2006 - IMAGE ANALYSIS

516

between the minimum and maximum grey lev-

els(Najman and Couprie, 2004). There exists links

between components at sequential grey levels in the

image. A component is deﬁned as:

= {x ∈ F/F (x) ≥ k} (1)

where F is an image and F

is a section k (level) of

F . The Connected Components (CC) of the different

cross-sections may be organized in order to form a

tree structure. We say that the two CCs C

k+1

and C

are linked when C

k+1

is a subset of C

(the inclusion

relation). The ﬁrst component C

(or C

min

) in the

image corresponds to the whole image domain and its

called root. Figure 2(b) shows the CT of the grayscale

image depicted in Figure 2(a).

(a) (b)

Figure 2: (a) The Component Tree of the grayscale image

of (b).

We can associate number to the CT nodes, which

measure some of the components features, such as:

mean graylevel of the component; mininum and max-

imum greylevel values; area; perimeter; and, the im-

age location of one representative pixel.

4.2 Filtering

Filtering the component tree is a decision-make

process which classiﬁed nodes into those that are ac-

tive (preserved) and those that are not (Jonnes, 1997).

A grey-level image is decomposed into a stack of bi-

nary images, which are processed individually by a

ﬁlter. When we re-stack these images, we have ob-

tained a grey-level ﬁlter and the segmented image is

obtained directly from the ﬁltered image. The ﬁlter-

ing algorithm can be summarized by the following 3

steps:

1. Tree computation – Compute the corresponding CT

for the image.

2. Computation of attributes – For all CT cross-

sections, compute the attributes area and grey level

mean that will be used in the segmentation analy-

sis.

3. Hierarchical analysis – Start the segmentation

analysis by the grey level criterion. Then, apply

the area criterion.

5 EXPERIMENTS

We present some results of yeast segmentation by

analysis of its hierarchy. Other results and analysis

are found in (Carvalho, 2004). The images were ob-

tained from School of Food Engineering (FEA - Fac-

uldade de Engenharia de Alimentos) at UNICAMP.

In all results we eliminate the objects that touch the

image frame. No markers are used in this approach.

Also, we use ST (survival time), area, ellipse ﬁtting

and gray level mean criteria in TCL analysis. The

yeast segmentation based on CT ﬁltering has accom-

plished by the utilization of grey-level mean and area

parameters of each component connected of the im-

age. All experiments are implemented in MATLAB.

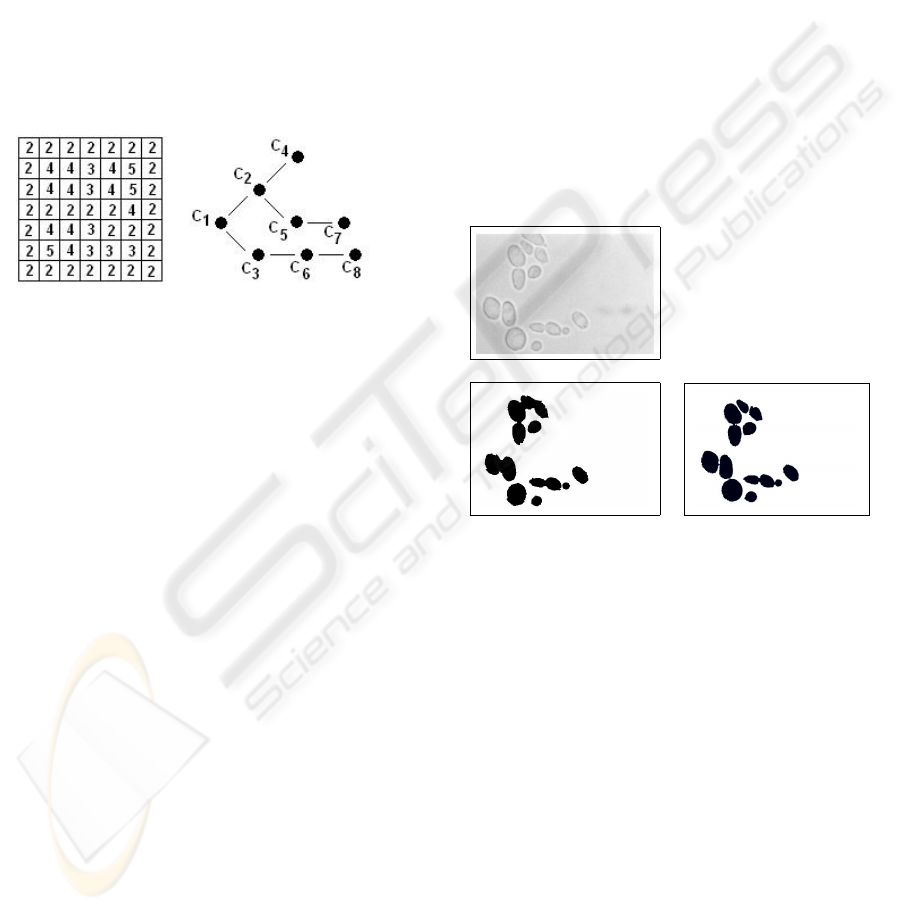
Figure 3 show an example of the yeast segmenta-

tion obtained from CT and TCL analysis. A detailed

observation of these images show that there are small

differences at border and connectivity between cells.

(a)

(b) (c)

Figure 3: (a) original image; (b) yeast segmentation by TCL

analysis; (c) yeast segmentation by CT analysis.

Figure 4 illustrates the comparison between three

different approachs in order to segment yeast cells.

Figure 4(d) show the segmented image of Figure 4(a),

obtained from O´Shea analysis (O´Shea and Walsh,

2000). In this case, it was necessary some morpholog-

ical operations (dilation, closing hole and erosion) in

order to remove some noises (regions not associated

to yeast cells) in the processed image. As we can see,

there are great differences between resulting images.

The main problems are the contour preservation, the

cells holes and the connectivity between cells. The

TCL approach, based on Watershed Transform, pre-

serve the cells contours; also, there is no holes.

Figure 5 show an last example of the yeast segmen-

tation obtained from TCL, CT and O´Shea analysis.

Comparison shows that the method based on TCL

representation preserves the yeast contours and pro-

vides cells area 10%, approximately, lower than CT

and O´Shea methods.

COMPARING YEAST CELLS SEGMENTATION THROUGH HIERARCHICAL TREES

517

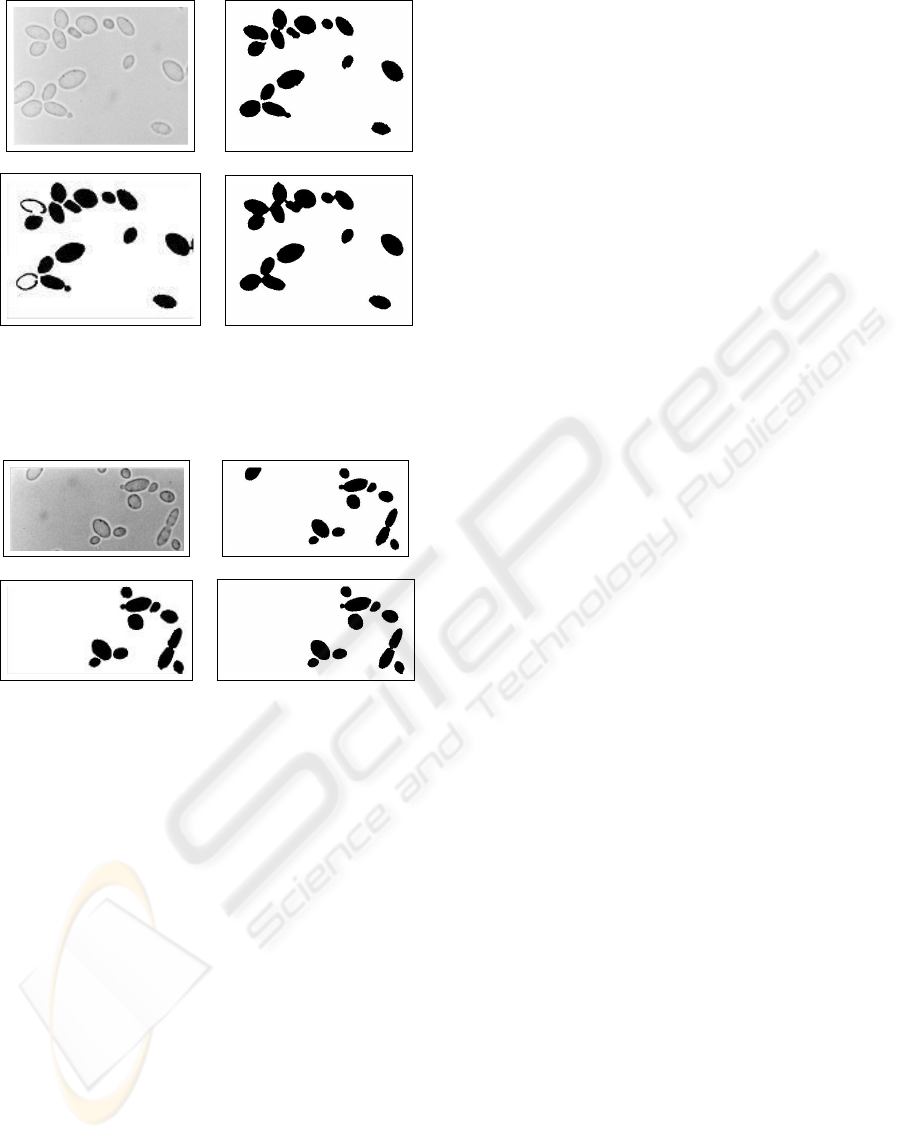
(a) (b)

Figure 4: (a) original image; (b) yeast segmentation by TCL

analysis; (c) yeast segmentation by CT analysis; (d)yeast

segmentation by O´Shea (O´Shea and Walsh, 2000) after

morphological operations.

(a) (b)

Figure 5: (a) original image; (b) yeast segmentation by TCL

analysis; (c) yeast segmentation by CT analysis; (d)yeast

segmentation by O´Shea (O´Shea and Walsh, 2000) after

morphological operations.

6 CONCLUSION

In this paper we presented an analysis based on tree repre-

sentation in order to segment yeast cells. We implemented

two approachs based on image representation by Tree of

Critical Lakes and Component Tree.

The results of the multiscale analysis for a group of yeast

images were satisfactory and demonstrated the robustness

of the method, even using few criteria. Usually, the clas-

sical Watershed is not able to segment correctly this type

of images, due to the lack of markers and also to the su-

persegmentation problem. Scale-space analysis is usually a

costly computational task. In the future, we will try to start

from coarser image partitions in order to reduce the range

of the computational analysis. Also, experiments was done

to segment yeast cells based on Component Tree ﬁltering.

The ﬁlter parameters used in this work were area and grey

level mean.

The investigations into the complexity of CT or TCL

computation algorithms are necessary in order to enhance

the efﬁcacy of the performance. Finally, experiments will

be done to classify yeast cells according to the taxonomy

presented by O´Shea (O´Shea and Walsh, 2000).

ACKNOWLEDGEMENTS

Tiago W. Pinto is grateful to FAPESP for the ﬁnancial sup-

port.

REFERENCES

Beucher, S. and Meyer, F. (1993). The morphological ap-

proach to segmentation: The watershed transforma-

tion. In Mathematical Morphology in Image Process-

ing, chapter 12. E. Dougherty, editor.

Carvalho, M. A. G. (2004). Hierarchical image analy-

sis through the tree of critical lakes (in portuguese).

In PhD Thesis, Electrical and Computer Engineering

Faculty, University of Campinas – UNICAMP, Brazil.

Fitzgibbon, A. W., Pilu, M., and Fisher, R. B. (1999). Direct

least squares ﬁtting of ellipses. In IEEE Transactions

on Pattern Analysis and Machine Intelligence.

Jonnes, R. (1997). Attributes signatures for connected ﬁl-

tering and segmentation. In Digital image and vision

computing:Techniques and aaplications. R. Chaplin

and W. Page (eds).

Mattes, J., Richard, M., and Demongeot, J. (1999). Tree

representation for image matching and object recog-

nition. In 8th International Conference on Discrete

Geometry for Computer Imagery. Springer.

Meyer, F. and Maragos, P. (1996). The dynamics of minima

and contours. In P. Maragos, R. W. Schafer and M. A.

Butt Editors, Mathematical Morphology and its Appli-

cations to Image and Signal Processing, pp.329-336.

Kluwer Academic Publishers.

Meyer, F. and Maragos, P. (1999). Multiscale morpholog-

ical segmentations based on watershed, ﬂooding and

eikonal pde. In Scale-Space Theory in Computer Vi-

sion, Second International Conference.

Najman, L. and Couprie, M. (2004). Quasi linear algorithm

for the component tree. In SPIE Vision Geometry.

O´Shea, D. G. and Walsh, P. K. (2000). The effect of the

culture conditions on the morphology of the dimor-

phic yeast Kluyveromyces marxianus var. marxianus

nrrly2415: a study incorporating image analysis. In

Applied Microbiology and Biotechnology.

Pons, M. N., Vivier, H., Rmy, J. F., and Dodds, J. A.

(1993). Morphological characterization of yeast by

image analysis. In Biotechnology and Bioengineer-

ing.

Vachier, C. (1995). Extraction de caracteristiques, segmen-

tation d´image et morphologie math

ematique. In PhD

Thesis, Centre de Morphologie Mathmatique, cole de

Mines de Paris, France.

VISAPP 2006 - IMAGE ANALYSIS

518