A NEW MULTISCALE, CURVATURE-BASED SHAPE

REPRESENTATION TECHNIQUE FOR CONTENT-BASED IMAGE

RETRIEVAL

JanKees van der Poel

Instituto de Educac¸

ao Superior da Para

ıba – IESP

ao Pessoa – Para

ıba – Brazil

Leonardo Vidal Batista, Carlos Wilson Dantas de Almeida

Departamento de Inform

atica – Universidade Federal da Para

ıba

ao Pessoa – Para

ıba – Brazil

Keywords:

Curvature Scale Space, CBIR, correlation coefﬁcient, resampling, resizing, shape classiﬁcation, full curvature

values.

Abstract:

This work presents a new multiscale, curvature-based shape representation technique for planar curves. One

limitation of the well-known Curvature Scale Space (CSS) method is that it uses only curvature zero-crossings

to characterize shapes and thus there is no CSS descriptor for convex shapes. The proposed method, on the

other hand, uses bidimentional→unidimentional→bidimentional transformations together with resampling

techniques to retain the full curvature information for shape characterization. It also employs the correlation

coefﬁcient as a measure of similarity. In the evaluation tests, the proposed method achieved a high correct

classiﬁcation rate (CCR), even when the shapes were severely corrupted by noise. Results clearly showed that

the proposed method is more robust to noise than CSS.

1 INTRODUCTION

Since the beginning of the 90s there has been an

increased research activity in the area of Content

Based Image Retrieval (CBIR). Not only large re-

search teams, such as IBM with the QBIC project, but

also small project groups in the academic and industry

worlds have devoted themselves to this task.

Image retrieval systems are supposed to retrieve

images in an effective manner based on a user’s input

query. This work aims to investigate ways of provid-

ing fast, easy and reliable access to images in elec-

tronic databases. It also intends to create a classiﬁ-

cation and retrieval system that will help to browse,

search, classify and retrieve images in large digitized

databases.

Image similarity is very subjective and relative to

each person actual needs: the more a person encoun-

ters an object, the more detailed and differently he or

she can describe it.

There are several simple image retrieval solutions

to the query problem. One of them is to annotate

images with text and then use a traditional textbased

search and retrieval. While fast, this is not effec-

tive when dealing with large collections of complex

images: variability of interpretation is enormous and

also is the human effort required for database anno-

tation. Effective image retrieval systems should ex-

ploit image attributes such as color distribution, mo-

tion, shape (Niblack et al., 1993), structure and tex-

ture (Batista and Meira, 2004).

Image retrieval is based on an ordering of match

scores obtained by searching through a database. The

key challenges in building a retrieval system are the

choice of attributes, their representations, query spec-

iﬁcation methods, match metrics and indexing strate-

gies.

Shape matching performs an important issue in im-

age retrieval by recognizing and classifying the im-

ages shapes. Some contour shape representations in-

clude eccentricity, circularity (Niblack et al., 1993),

chain code (Freeman and Saaghri, 1978), centroid

distance, cumulative angles (Davies, 1997), Fourier

descriptors, Wavelet descriptors (Zahn and Roskies,

1972; Persoon and Fu, 1977; Kauppinen et al., 1995;

Tieng and Boles, 1997; Yang et al., 1998; Loncaric,

1998) and Curvature Scale Space (CSS) descrip-

tors (Mokhtarian and Mackworth, 1992; Mokhtarian,

1995; Mokhtarian et al., 1996b; Abbasi et al., 2000).

It is generally accepted that CSS descriptors

achieve a good compromise between representation

power and computational efﬁciency (Dudek and Tsot-

401

van der Poel J., Vidal Batista L. and Wilson Dantas de Almeida C. (2006).

A NEW MULTISCALE, CURVATURE-BASED SHAPE REPRESENTATION TECHNIQUE FOR CONTENT-BASED IMAGE RETRIEVAL.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 401-406

DOI: 10.5220/0001372304010406

 SciTePress

sos, 1997; Daoudi and Matusiak, 2000; Mokhtarian

et al., 1996a). The curvature of a planar curve has

perceptual characteristics that have proven to be use-

ful for shape recognition (Pomerantz et al., 1977),

being one of the most powerful tools for representa-

tion, interpretation and recognition of objects in an

image (Mokhtarian and Mackworth, 1992; Pavlidis,

1980; Mokhtarian and Mackworth, 1986; Dudek and

Tsotsos, 1997)). Such characteristics made CSS to be

selected as one of the MPEG-7 contour shape descrip-

tors (Mokhtarian and Bober, 1998).

This paper presents a new method for shape charac-

terization suitable to be used as a retrieval tool in large

image collections. This method is based on the clas-

sical CSS method but but all the available curvature

information is used to perform shape matching, in-

stead of using only the curvature zero-crossing points.

It also uses the correlation coefﬁcient as a measure

of similarity between shapes, allowing a high correct

classiﬁcation rate, even when the shapes are severely

corrupted by uniform random noise.

The rest of the paper is organized as follows: Sec-

tion 2 describes and discusses the classical CSS de-

scriptor; Section 3 describes the proposed method

and compares it with the classical CSS method; Sec-

tion 4 shows qualitative results of retrieval tests ob-

tained from direct comparison between the classical

CSS method and the proposed method; and Section 5

presents a discussion of the results and the concluding

remarks.

2 CURVATURE SCALE SPACE

METHOD

The classical Curvature Scale Space method for con-

tour representation captures, describes and compares

characteristic shape features of objects based on their

closed contours. It is a multiscale representation of

the inﬂexion points of a closed contour (Mokhtarian

and Mackworth, 1992), is considered a reliable and

very fast method to perform shape analysis in large

databases and has a number of important properties,

such as:

1. It captures the main features of a shape, enabling

similarity-based retrieval;

2. It reﬂects properties of the human visual system

perception and offers good generalization;

3. It is robust to non-rigid motion, partial occlusion of

the shape, noise and changes in scale and orienta-

tion;

4. It is robust to perspective transformations that re-

sult from common changes of camera parameters

in images and video; and

5. It is compact, reliable and fast.

The idea behind the classical CSS is that a contour

can be represented by its curvature values. It is pos-

sible to compute the curvature at each contour point

based on its neighboring points (Haralik and Shapiro,

1992). The classical CSS takes into account only

those points where the curvature goes from a posi-

tive to a negative value, or vice-versa (curvature zero-

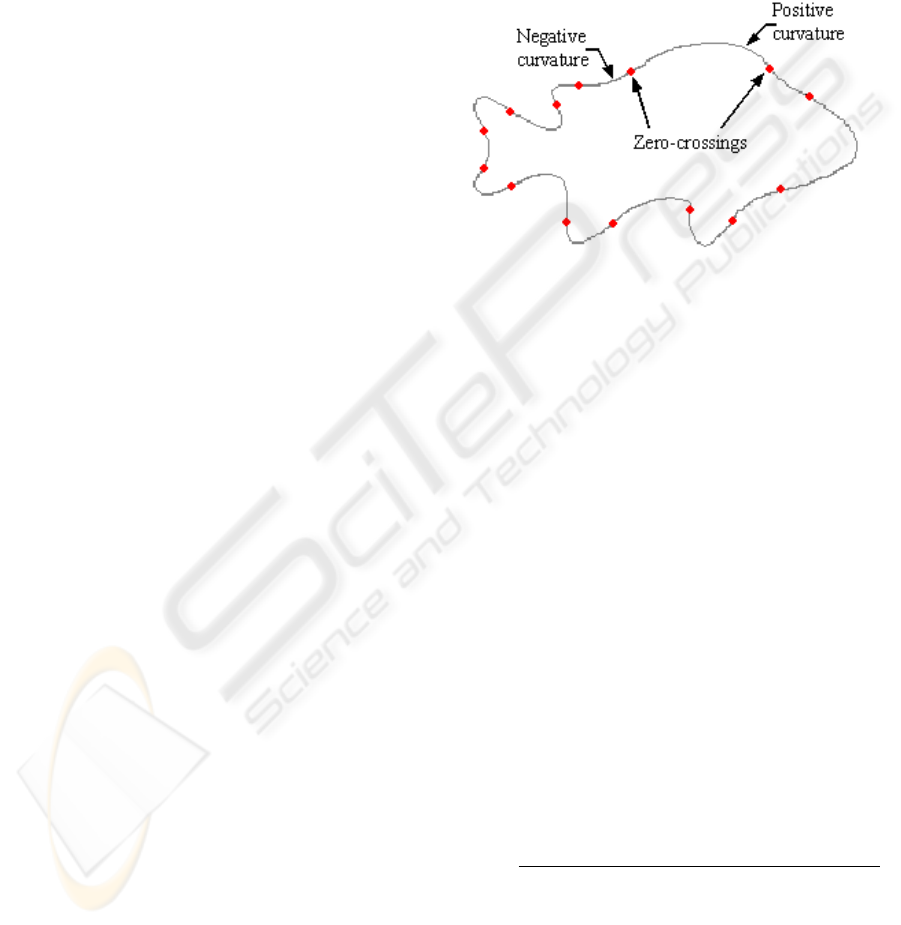
crossings), as illustrated in Figure 1.

Figure 1: Curvature zero-crossings.

To compute the classical CSS representation of a

given object, its contour Γ is initially obtained and

parametrized as in Equation 1.

Γ(u)={(x(u),y(u)) |u ∈ [0, 1]} (1)

where u is the normalized arc length parameter, vary-

ing between 0 and 1, and (x(u),y(u)) are parametric

coordinates sampled from the contour at equidistant

values of u, starting at an arbitrary contour point and

following in counterclockwise direction.

Convolving the parametric coordinates of Γ with

a progressively higher standard deviation σ 1-

D Gaussian kernel generates the evolved version

(Mokhtarian and Mackworth, 1992) of Γ, deﬁned

as in Equation 2.

(u, σ)=(X(u, σ),Y(u, σ)) (2)

where X(u, σ)=x(u) ∗ g(u, σ), Y (u, σ)=y(u) ∗

g(u, σ),“∗” is the convolution operator and g(u, σ) is

a Gaussian with standard deviation σ.

The curvature k(u, σ) of Γ

is given by Equa-

tion 3 (Mokhtarian and Mackworth, 1992):

κ(u, σ)=

(u, σ) · Y

(u, σ) − X

(u, σ) · Y

(u, σ)

+ Y

(u, σ)

)

3/2

(3)

where X

(u, σ)=x(u) ∗ g

(u, σ), Y

(u, σ)=

y(u) ∗ g

(u, σ), X

(u, σ)=x(u) ∗ g

(u, σ) and

(u, σ)=y(u) ∗ g

(u, σ).

After each convolution step, the curvature zero-

crossings of k(u, σ) are located by computing the

VISAPP 2006 - IMAGE ANALYSIS

402

curvature for all contour points with Equation 3 us-

ing progressively higher values of σ and determining

where the curvature goes from a positive to a negative

value, and vice-versa. This is done until the curve Γ

becomes completely convex.

Finally, the CSS Image of Γ is a binary image de-

ﬁned by the zero-crossing points of k(u, σ), with u

values in the horizontal axis and σ values in the verti-

cal axis.

As each convolution step smooths the shape con-

tour, the zero-crossings will group two by two, ap-

proach each other, merge and ﬁnally disappear, form-

ing what is called a CSS peak. Each zero-crossing

does not necessarily group with an adjacent zero-

crossing: at the end smaller peaks can exist inside

larger ones, due to contour sections delimited by two

zero-crossings that are close together.

To perform a CSS shape-based retrieval, the sim-

ilarity between two shapes is measured by the sum

of the peak differences between all the matched

peaks and the peak values of all the unmatched

peaks (Mokhtarian, 1995; Mokhtarian et al., 1996a;

Mokhtarian et al., 1996b; Abbasi et al., 2000).

Below there is a summary of the steps performed

when using the classical CSS method:

1. Image segmentation;

2. Contour extraction;

3. Shape scale normalization, done by sampling the

shape boundary into a ﬁxed number of points to al-

low matching shapes with different boundary sizes;

4. Shape curvature computation;

5. CSS Image computation; and

6. Shape matching.

Matching CSS Images is difﬁcult because they usu-

ally have a different number of CSS peaks, these

peaks are usually not matching and also can be or-

dered in a quite different way. Mirrored and ﬂipped

shapes need to be considered separately too.

In addition, the classical CSS method only captures

local shape features, missing the global ones (which

are important to shape representation too). To over-

come this, global features such as eccentricity, circu-

larity and number of CSS peaks should be combined

in order to correctly describe the shapes (Zhang and

Lu, 2001).

Due to the dependence on curvature zero crossings,

convex objects may not be well represented with the

classical CSS method. This means that shapes like

circles, ellipsis or convex polygons may not be recog-

nized using this method.

As a ﬁnal drawback of the classical CSS method,

the boundary sampling and the thresholding processes

done when extracting the CSS peaks causes the CSS

Image to not reﬂect the true number of convex (or

concave) segments on the shape boundary.

3 PROPOSED METHOD – FULL

CURVATURE SCALE SPACE

METHOD

Considering all the classical CSS method problems, a

new approach to retrieve an image based on its con-

tour will now be described.

The proposed method basically performs the same

computations of the classical CSS method. The main

differences are:

1. Its unnecessary to perform the CSS Image compu-

tation step;

2. Full curvature information usage (and not only the

zero-crossing information); and

3. The shape matching step, which uses a different ap-

proach.

The proposed method matches shapes using a Full

CSS matrix. This matrix has all the curvature values

computed from Equation 3 with progressively higher

values of σ.

To perform shape matching, the CSS matrices of

the shapes under analysis are computed and com-

pared using the 2-D correlation coefﬁcient r, shown

in Equation 4.

r =





σu

−



σu

−















σu

−









σu

−





(4)

where A, B are the CSS matrices of shapes A and B

and

B their means, respectively.

As the classical CSS method, the proposed method

suffers from the problem related to the the contour

following arbitrary starting point. To solve this, a one

column rotation is performed to the matrix belonging

to the original shape (the one that is being compared

to the other shapes in the database) each time the cor-

relation coefﬁcient between them is computed.

If one shape has deeper concavities than other, the

σ value used to smooth them completely can be differ-

ent, leading to curvature matrices with non-matching

heights. In this case, directly computing r with Equa-

tion 4 will not be possible. To overcome this, the cur-

vature matrix with the smaller number of lines is re-

sampled to the same number of lines of the higher

curvature matrix.

For noise contaminated shapes, initially the pro-

posed method has results that are worse than those

achieved by the classical CSS method: as the pro-

posed method takes into account all the curvature in-

formation, and as the ﬁrst lines of the Full CSS matrix

A NEW MULTISCALE, CURVATURE-BASED SHAPE REPRESENTATION TECHNIQUE FOR CONTENT-BASED

IMAGE RETRIEVAL

403

Figure 2: Fish kk4 and its noise contaminated versions (noise ranges of [−3, 3], [−6, 6], [−9, 9] and [−12, 12], respectively,

from column two to ﬁve).

are those corresponding to the contour without being

smoothed enough, this leads to wrong classiﬁcations

results. To solve this problem, the shape smoothing

process of the proposed method can be started with

a higher σ value, generating a new Full CSS matrix,

which then will be used to perform the comparison

tests.

Having computed all the correlation coefﬁcients

between the two curvature matrices, one for each ro-

tation, the highest coefﬁcient among all is chosen to

be the similarity measure between the two shapes.

The higher this coefﬁcient is, the more similar are the

shapes.

This procedure has the advantage of keeping the

information related to the curvatures of the shapes,

allowing for a more precise matching between them.

4 EXPERIMENTAL RESULTS

In this section, a comparison between the classical

CSS method and the proposed Full CSS method in

terms of retrieval results is done.

For sake of comparison, tests were made with two

initial σ values (σ =1and σ =10) when computing

the curvature matrices at the classiﬁcation stage.

To test the retrieval performance of the classical

CSS and the proposed FCSS method, a Matlab



based indexing and retrieval framework was imple-

mented on Microsoft



Windows



XP Professional

running on a PC Athlon64 platform.

For the tests, a small database set, comprising the

ﬁrst one hundred ﬁsh contours (from kk1 to kk100)

from the ﬁsh contours database available at (Abbasi

et al., 2005), was selected. The classical CSS method

was implemented using the same matching algorithm

described in (Mokhtarian and Abbasi, 2002).

Classiﬁcation accuracy was measured by the Cor-

rect Classiﬁcation Rate (CCR), as in Equation 5:

CF =

× 100% (5)

where c is the number of correctly classiﬁed contours,

and t is the number of classiﬁed contours.

Each contour was compared to itself and to all oth-

ers belonging to the test database. To test the ro-

bustness of the proposed methods under noisy con-

ditions, uniform random noise in the ranges [−3, 3],

0 [−3,3] [−6,6] [−9,9] [−12,12]

100

Range of uniform noise added to contours

CCRs (%)

Correct Classification Rate achieved by CSS, FCSS

σ=1

and FCSS

σ=10

Classical CSS

Full CSS with σ=1

Full CSS with σ=10

Figure 3: CCRs achieved by CSS, FCSS

σ=1

and

FCSS

σ=10

[−6, 6], [−9, 9] and [−12, 12] was added to each con-

tour. Again, each contour was compared to all noise

contaminated contours of the test database. Figure 2

shows one of the contours (and its noise contaminated

versions) used to perform the comparison tests be-

tween the methods discussed in this work.

Table 1 and Figure 3 both summarize the test re-

sults for the classical CSS method along with the

results for FCSS

σ=1

and FCSS

σ=10

, presenting the

CCRs achieved by each method versus the range of

uniform noise added to the shapes.

Figure 4 presents the retrieval results achieved by

FCSS with σ =10in a shape similarity query using

the ﬁsh contour kk2. This test was done to visually

assess the accuracy of the proposed method: the sys-

Table 1: CCRs achieved by the classical CSS method,

FCSS

σ=1

and FCSS

σ=10

for the test shapes.

Amplitude CCR (%)

of the random Classical FCSS FCSS

uniform noise CSS method σ =1 σ =10

0 (no noise) 100 100 100

[−3, 3] 94 89 99

[−6, 6] 91 81 98

[−9, 9] 80 65 98

[−12, 12] 67 57 95

VISAPP 2006 - IMAGE ANALYSIS

404

Figure 4: Similarity retrieval test results, ordered from the

most similar to the less similar according to the system an-

swer: (a) shape used as query (kk2); (b) kk2; (c) kk13; (d)

kk31; (e) kk22; and (f) kk20.

tem was set to return the ﬁve more similar shapes to

the one chosen. The ﬁve ﬁshes returned were kk2 it-

self, kk13, kk31, kk22 and kk20, ordered by similarity

according to the system answer.

The time spent by the proposed method to retrieve

one shape from the database was about 19 seconds.

This means that, given one shape, the system spent

19 seconds to retrieve 100 other shapes and return the

correct (or incorrect) shape matching the given one.

The classical CSS method spent 15 seconds to per-

form the same retrieval task.

The memory needed for each Full CSS matrix is

the same as for an image of size about 300×200. The

Matlab



implementation used in this work stored the

FCSS data as an array of 16 bit-unsigned integers,

meaning that one FCSS matrix has about 480 K bytes.

This memory amount can be reduced by using an ar-

ray of 8 bit-unsigned integers.

5 CONCLUSIONS

This paper proposed a new, simple and highly ac-

curate shape classiﬁcation scheme based on the well

known CSS method. The main innovations of the new

representation scheme over the classical CSS method

are the use of all curvature information available, of

different initial σ values to improve the retrieval per-

formance and of the correlation factor as a similarity

measure.

It is worth to say that in (Junior and da Costa,

1998), a similar multiscale, curvature-based shape

representation method was shown, but the author only

describes his technique and does not show any results

regarding its shape retrieval performance. Besides

that, his method uses Fourier Transforms and is not

directly related to the CSS method.

To assess the performance of the classical CSS and

the FCSS method, the test shapes were contaminated

with random uniform noise ranging from low to high

amplitudes and a database shape retrieval was done,

as described in Section 4.

Evaluating the effects of adding noise to the test

shapes over classiﬁcation accuracy, as in Figure 3,

showed that the performance of the classical CSS

method quickly degrades. This is due to the fact

that when noise range goes beyond [−6, 6], important

regions of the contour will overlap (as can be seen

in Figure 2). In contrast, when using σ =10the

proposed classiﬁer maintains its performance even in

presence of severe noise, as can be seen in Figure 3.

Table 1 and Figure 3 together show that the FCSS

method with σ =10achieved CCR = 95% with noise

amplitudes up to [−12, 12], while the classical CSS

method achieved only CCR = 67% under the same

condition.

The robustness of the proposed method under noisy

conditions should be pointed: a retrieval for similar

shapes showed very good results, as can be seen from

Figure 4.

Table 1 shows that simply increasing the σ initial

value also increased the classiﬁer performance: for

a noise with amplitude range [−12, 12], the classical

CSS method achieved CCR = 67% while the FCSS

method with σ =10achieved CCR = 95% (a much

better result than the FCSS method with σ =1, which

only achieved CCR = 57%).

The time spent in a simple query by the proposed

method is still high. This is due to the fact that all the

test platform was implemented using interpreted code

in Matlab



without any speed optimization. The au-

thors are now implementing the same test framework

in Java, seeking for a more efﬁcient retrieval.

It is clear that the proposed method consistently

outperforms the classical CSS method. This superior-

ity is still more remarkable when shapes are severely

contaminated by noise and shows that the proposed

method is suitable to be used in such conditions.

Other research directions include more tests to as-

sess the classiﬁcation and retrieval results under dif-

ferent types of noise; investigate the performance

of the FCSS method in other domains, such as tu-

mor classiﬁcation and recognition (de Almeida et al.,

2005), and in shapes with large boundary indentations

and protrusions; and investigate the use of dictionary

created by lossless data compression algorithms, such

as LZW or PPM, instead of the correlation coefﬁcient

as the similarity measure (Batista and Meira, 2004).

A NEW MULTISCALE, CURVATURE-BASED SHAPE REPRESENTATION TECHNIQUE FOR CONTENT-BASED

IMAGE RETRIEVAL

405

ACKNOWLEDGMENTS

The authors wish to thank Professor Fernando Manuel

Bernardo Pereira, from Instituto Superior T

ecnico,

Lisboa, for his valuable contribution to our Image

Processing Group, and Professor Farzin Mokhtarian

for his ﬁsh contour database.

REFERENCES

Abbasi, S., Mokhtarian, F., and Kittler, J. (2005).

Search for similar shapes in the squid system:

Shape queries using image databases. World

Wide Web, http://www.ee.surrey.ac.uk/

Research/VSSP/imagedb/demo.html.

Abbasi, S., Mokhtarian, F., and Kittler, J. V. (2000). En-

hancing CSS-based shape retrieval for objects with

shallow concavities. Image and Vision Computing,

18(3):199–211.

Batista, L. V. and Meira, M. M. (2004). Texture classiﬁca-

tion using the Lempel-Ziv-Welch algorithm. In Pro-

ceedings of the 17th Brazilian Symposium on Artiﬁcial

Intelligence, pages 444–453, S

ao Lu

ıs, Maranh

ao,

Brazil.

Daoudi, M. and Matusiak, S. (2000). Visual image retrieval

by multiscale description of user sketches. Journal of

Visual Languages and Computing, 11(3):287–301.

Davies, E. R. (1997). Machine Vision: Theory, Algorithms,

Practicalities. Academic Press, 1st edition.

de Almeida, C. W. D., v. d. Poel, J., Batista, L. V., and

de Amorim, H. L. E. (2005). An

alise de Formas

Baseada no M

etodo da Curvature Scale Space para

Tumores de C

ancer de Mama. In Proceedings of the

Brazilian Computer Society – SBC – WIM 2005, pages

1–4. Brazilian Computer Society – SBC.

Dudek, G. and Tsotsos, J. K. (1997). Shape representation

and recognition from multiscale curvature. Computer

Vision and Image Understanding, 68(2):170–189.

Freeman, H. and Saaghri, A. (1978). Generalized chain

codes for planar curves. In Proceedings of the 4th In-

ternational Joint Conference on Pattern Recognition,

pages 701–703.

Haralik, R. M. and Shapiro, L. G. (1992). Computer and

Robot Vision. Vol. I. Addison-Wesley, Reading, MA.

Junior, R. M. C. and da Costa, L. F. (1998). Towards effec-

tive planar shape representation with multiscale digi-

tal curvature analysis based on signal processing tech-

niques. Pattern Recognition, 29(9):1559–1569.

Kauppinen, H., Seppanen, T., and Pietikainen, M. (1995).

An experimental comparison of autoregressive and

Fourier-based descriptors in 2d shape classiﬁcation.

IEEE Trans. Pattern Anal. Mach. Intell., 17(2):201–

207.

Loncaric, S. (1998). A survey of shape analysis techniques.

Pattern Recognition, 31(8):983–1001.

Mokhtarian, F. (1995). Silhouette-based isolated object

recognition through Curvature Scale Space. IEEE

Trans. Pattern. Anal. Mach. Intell., 17(5):539–544.

Mokhtarian, F. and Abbasi, S. (2002). Shape similarity re-

trieval under afﬁne transforms. Pattern Recognition,

35(1):31–41.

Mokhtarian, F., Abbasi, S., and Kittler, J. (1996a). Robust

and efﬁcient shape indexing through Curvature Scale

Space. In Proceedings of British Machine Vision Con-

ference, pages 53–62.

Mokhtarian, F., Abbasi, S., and Kittler, J. V. (1996b). Ef-

ﬁcient and robust retrieval by shape content through

Curvature Scale Space.

Mokhtarian, F. and Bober, M. (1998). Curvature Scale

Space Representation: Theory, Applications and

MPEG-7 Standardisation. Springer, 1st edition.

Mokhtarian, F. and Mackworth, A. K. (1986). Scale based

description and recognition of planar curves and two-

dimensional shapes. IEEE Trans. Pattern. Anal. Mach.

Intell., 8(1):34–43.

Mokhtarian, F. and Mackworth, A. K. (1992). A theory of

multiscale, curvature-based shape representation for

planar curves.

IEEE Trans. Pattern. Anal. Mach. In-

tell., 14(8):789–805.

Niblack, W., Barber, R., Equitz, W., Flickner, M., Glasman,

E., Petkovic, D., Yanker, P., Faloutsos, C., and Taubin,

G. (1993). The QBIC project: querying images by

content using color, texture and shape. In Proceedings

of the SPIE - The International Society for Optical En-

gineering, volume 1908, pages 173–187.

Pavlidis, T. (1980). Algorithms for shape analysis of con-

tours and waveforms. IEEE Trans. Pattern Analysis

and Machine Intelligence, 2(4):301–312.

Persoon, E. and Fu, K. S. (1977). Shape discrimination

using Fourier descriptors. IEEE Transactions on Sys-

tems, Man and Cybernetics, SMC-7(3):170–179.

Pomerantz, J. R., Sager, L. C., and Stoever, R. J. (1977).

Perception of wholes and of their component parts:

some conﬁgural superiority effects. Journal of exper-

imental psychology, 3(3):422–435.

Tieng, Q. and Boles, W. W. (1997). Recognition of 2d

object contours using the wavelet transform zero-

crossing representation. IEEE Trans. Pattern Anal.

Mach. Intell., 19(8):910–916.

Yang, H. S., Lee, S. U., and Lee, K. M. (1998). Recognition

of 2d object contours using starting-point-independent

wavelet coefﬁcient matching. Journal of Visual Com-

munication and Image Representation, 9:171–181.

Zahn, C. and Roskies, R. (1972). Fourier descriptors for

plane closed curves. IEEE Transactions on Comput-

ers, C–21:269–281.

Zhang, D. and Lu, G. (2001). Content-based shape re-

trieval using different shape descriptors: A compara-

tive study. In Proc. of IEEE International Conference

on Multimedia and Expo (ICME2001), pages 317–

320, Tokyo, Japan.

VISAPP 2006 - IMAGE ANALYSIS

406