A BACKGROUND MODELLING ALGORITHM BASED ON

ENERGY EVALUATION

Paolo Spagnolo, Tiziana D’Orazio, Marco Leo, Nicola Mosca, Massimiliano Nitti

Istituto di Studi sui Sistemi Intelligenti per l’Automazione - CNR, Via Amendola 122/D, 70126 Bari,Italy

Keywords: Motion Detection, Background Subtraction, Background Modeling.

Abstract: Detecting moving objects is very important in many application contexts such as people detection, visual

surveillance, automatic generation of video effects, and so on. The first and fundamental step of all motion

detection algorithms is the background modeling. The goal of the methodology here proposed is to create a

background model substantially independent from each hypothesis about the training phase, as the presence

of moving persons, moving background objects, and changing (sudden or gradual) light conditions. We

propose an unsupervised approach that combines the results of temporal analysis of pixel intensity with a

sliding window procedure to preserve the model from the presence of foreground moving objects during the

building phase. Moreover, a multilayered approach has been implemented to handle small movements in

background objects. The algorithm has been tested in many different contexts, in both indoor and outdoor

environments. Finally, it has been tested even on the CAVIAR 2005 dataset.

1 INTRODUCTION

Many computer vision tasks require robust

segmentation of foreground objects from dynamic

scenes; this general assertion is particularly true for

video surveillance applications. The most used

algorithms for moving objects detection are based on

background subtraction: the foreground objects are

extracted by subtracting the current image from a

reference background model. Therefore, the first and

crucial step of these kind of algorithms is the

background creation.

Many algorithms proposed in literature in the last

years present some common characteristics. Usually,

independently from the applicative context, the main

features that each background modeling algorithm

has to handle are:

• Presence of foreground and/or moving

background objects during the model

building phase;

• Gradual and/or sudden variations in

illumination conditions.

Many authors have dealt with the problem of

background modeling, as both a stand-alone task or

a module in a complete motion detection system.

A first group of algorithms uses statistical

approaches to model background pixels. In

(Wren,1997 and Kanade,1998) a pixel-wise gaussian

distribution was assumed to model the background.

In (Wren,1997) the algorithm was used for an indoor

motion detection system, whereas in (Kanade,1998)

the authors tested the algorithm in outdoor contexts.

However, the presence of foreground objects during

the building phase could cause the creation of an

unreliable model, such as in presence of light

movements in the background objects, or sudden

light changes. These observations suggest that

probably the proposed algorithms work well in

presence of a supervised training, during which ideal

conditions are granted by the human interaction.

The natural evolution of these approaches was

proposed in (Stauffer,1999). In this work a

generalized mixture of gaussians was used to model

complex non-static background. In this way the

great drawback of the moving background objects

was solved by using many gaussians to model

crucial pixels in that regions. However, the presence

of foreground objects during this phase could

heavily alter the reliability of the model immediately

after the creation phase, like happened under sudden

light changes.

The approach proposed in (Haritaoglu,1998) was

conceptually similar to that proposed in

(Wren,1997). But in this work the authors did not

construct a real gaussian distribution, while they

422

Spagnolo P., D’Orazio T., Leo M., Mosca N. and Nitti M. (2006).

A BACKGROUND MODELLING ALGORITHM BASED ON ENERGY EVALUATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 422-427

DOI: 10.5220/0001373404220427

 SciTePress

preferred to maintain general statistics for each point

(minimum and maximum values registered, max

difference between two consecutive values). In this

way they cope with the movements in background

objects, even if they waive a correct segmentation of

foreground objects in those regions. However, like

previous works, they could encounter misdetection

in presence of foreground objects during the

modeling phase. The natural improvement of this

approach was proposed in (Kim,2004): the basic

idea of (Haritaoglu,1998) was iterated in order to

build a codebook for each point, providing a set of

different possible values for each point. This

algorithm was conceptually similar to the mixture of

gaussians proposed in (Stauffer,1999), and the

experimental results proposed by the authors

appeared interesting.

All previous approaches use statistical

information, at different complexity level, for the

background modeling.

A different category is composed by the

approaches that use filters for temporal analysis. In

(Koller,2004) authors used a Kalman-filter approach

for modeling the state dynamics for a given pixel. In

(Elgammal,2000) a non-parametric technique was

developed for estimating background probabilities at

each pixel from many recent samples over time

using Kernel density estimation. In (Doretto,2003)

an autoregressive model was proposed to capture the

properties of dynamic scenes. A modified version of

this algorithm was implemented in (Monnet,2003,

and Zhong,2003) to address the modelling of

dynamic backgrounds and perform foreground

detection. In (Toyama,1999) a modified version of

the Kalman filter, the Weiner filter, was used

directly on the data. The common assumption of

these techniques was that the observation time series

were independent at each pixel.

All the approaches above presented were tested

on real sequences, producing interesting results,

even if each of them suffered in almost one of the

critical situations listed above. The approaches that

apparently were able to work well in every

conditions implicitly require a supervised

background model construction, in order to prevent,

critical situations.

In this work we present a background modeling

algorithm able to face all the crucial situations

typical of a motion detection system with an

unsupervised approach; no assumptions about the

presence/absence of foreground objects and changes

in light conditions was required. The main idea is to

exploit the pixels energy information in order to

distinguish static points from moving ones. To make

the system more reliable and robust, this procedure

has been integrated in a sliding windows approach,

that is incrementally maintained during the training

phase; in this way the presence of sudden light

changes and foreground objects is correctly handled,

and it does not alter the final background model. In

order to cope with the presence of moving

background objects, a multilayered modeling

approach has been implemented, combining

temporal and energetic information.

In the rest of the paper the details of the whole

procedure will be explained, and then the

experimental results obtained on real image

sequences will be reported.

2 BACKGROUND MODEL

The main goal of a modeling algorithm is to create a

reliable model limiting the memory requirements. In

an ideal case the best background model could be

created by observing a-posteriori all the frames of

the training phase; however this solution is not

reasonable then one of the constraint of our

approach is to work in an incrementally mode, to

reduce hardware requirements, without losing the

reliability.The implemented background modeling

algorithm is based on two distinct phases; each of

them tries to solve a particular modeling problem

(see par. 1).

Firstly, the energy information of each image

point, evaluated in a small sliding temporal window,

is used to distinguish static points from moving

ones. In this way we are able to obtain a statistical

background model with only the contribution of

background points, without the effects of foreground

objects. However, with this proposed technique, the

small movements of the background objects are not

included in the model.

3 ENERGY INFORMATION

One of the main problems of background modeling

algorithm is their sensitiveness to the presence of

moving foreground objects in the scene.

The proposed algorithm exploits the temporal

analysis of the energy of each point, evaluated by

means of sliding temporal windows. The basic idea

is to analyze in a small temporal window the energy

information for each point: the statistical values

relative to slow energy points are used for the

background model, while they are discarded for high

A BACKGROUND MODELLING ALGORITHM BASED ON ENERGY EVALUATION

423

energy points. In the current temporal window, a

point with a small amount of energy is considered as

a static point, that is a point whose intensity value is

substantially unchanged in the entire window;

otherwise it corresponds to a non static point, in

particular it could be:

• a foreground point belonging to a

foreground object present in the scene;

• a background point corresponding to a

moving background object.

At this level, these two different cases will be

treated similarly, while in the next section a more

complex multilayer approach will be introduced in

order to correctly distinguish between them.

A coarse-to-fine approach for the background

modeling, is applied in a sliding window of size W

(number of frames). The first image of each window

is the coarse background model. In order to have an

algorithm able to create at runtime the required

model, instead of building the model at the end of a

training period, as proposed in (Lipton,2002), the

mean (1) and standard deviation (2) is evaluated at

each frame; then, the energy content of each point is

evaluated over the whole sliding window, to

distinguish real background points from the other

ones. Formally, for each frame the algorithm

evaluates mean and standard deviation, as proposed

in (Kanade,1998):

)1(),(),(

−

−+=

ttt

yxyx

μααμμ

(1)

)1(|),(),(|),(

−

−+−=

tttt

yxyxyx

σαμμασ

(2)

only if the intensity value of that point is

substantially unchanged with respect to the coarse

background model, that is:

thyxByxI

<− ),(),( (3)

where th is a threshold experimentally selected and

(x,y) is the intensity value of point (x,y) at time t..

In this way, at the end of the analysis if the first

W frames, for each point the algorithm evaluates the

energy content as follows:

),(),(),(

∫

∈

−=

yxByxIyxE (4)

The first fine model of the background BF is

generated, as

⎩

⎨

⎧

)(),(

)(),()),(),,((

),(

WthyxEif

WthyxEifyxyx

yxB

σμ

(5)

A low energy content means that the considered

point is a static one and the corresponding statistics

are included in the background model, whereas high

energy points, corresponding to foreground or

moving background objects cannot contribute to the

model. The whole procedure is iterated on another

sequence of W frames, starting from the frame W+1.

The coarse model of the background is now the

frame W+1, and the new statistical values (1) and

(2) are evaluated for each point, like as the new

energy content (4). The relevant difference with (5)

is that now the new statistical parameters are

averaged with the previous values, if they are

present; otherwise, they become the new statistical

background model values. Formally, the new

formulation of (5) become:

⎪

⎩

⎪

⎨

⎧

≠∧<

−+

=∧

)(),(

),()(),(

)),(),,((*)1(),(*

),(

)(),()),(),,((

),(

WthyxEif

yxBWthyxEif

yxyxyxB

yxB

WthyxEifyxyx

σμββ

σμ

(6)

The parameter β is the classic updating parameter

introduced in several works on background

subtraction ((Wren,1997), (Kanade,1998),

(Haritaoglu,1998)). It allows to update the existent

background model values to the new light conditions

in the scene.

The whole procedure is iterated N times, where N

could be a predefined value experimentally selected

to ensure the complete coverage of all pixels.

Otherwise, to make the system less dependent from

any a-priori assumption, a dynamic termination

criteria is introduced and easily verified; the

modeling procedure stops when a great number of

background points have meaningful values:

0)),((#

≅

yxB

(7)

4 MULTILAYER ANALYSIS

The approach described above allows the creation of

a reliable statistical model for each point of the

image, even if temporarily covered by moving

objects. However, it is not able to distinguish

movements of the background objects (for example,

a tree blowing in the wind) from foreground objects.

So, the resulting model is very sensitive to the

presence of small movements in the background

objects, and this is a crucial problem, especially in

outdoor contexts.

The solution we propose uses a temporal analysis

of the training phase in order to automatically learn

if the detected movement is due to the presence of a

foreground or a moving background object. The

starting point is the observation that, if a foreground

object appears in the scene, the variation in the pixel

intensity levels is unpredictable, without any logic

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

424

and/or temporal meaning. Otherwise, in presence of

a moving background object, there will be many

variations of approximately the same magnitude,

even if these variations will not have a fixed period

(this automatically excludes the possibility to use

frequency-based approaches, i.e. Fourier analysis).

In order to motivate this assumption, we have

analysed the mean values registered in some points

belonging to the different image regions over a long

observation period (in fig. 1 some images of this

sequence are reported).

Figure 1: some images of the examined sequence.

The first group is composed by static background

points (zone A in the first image of fig. 1), while the

second (B) is composed by moving background

points (background points that are temporarily

covered by a moving tree). The third group (C)

corresponds to some static adjacent background

points that are covered by both moving people and a

moving tree. Finally, the last region (D) corresponds

to a region covered by only foreground objects. We

have chosen to select a group of points for each class

instead of a single point to reduce the effects of

noise; on the other hand, for each group, the selected

points are very spatially closed, because of their

intensity values need to be similar for a correct

analysis of their variations comprehension. Indeed,

the values assumed by each point in the same group

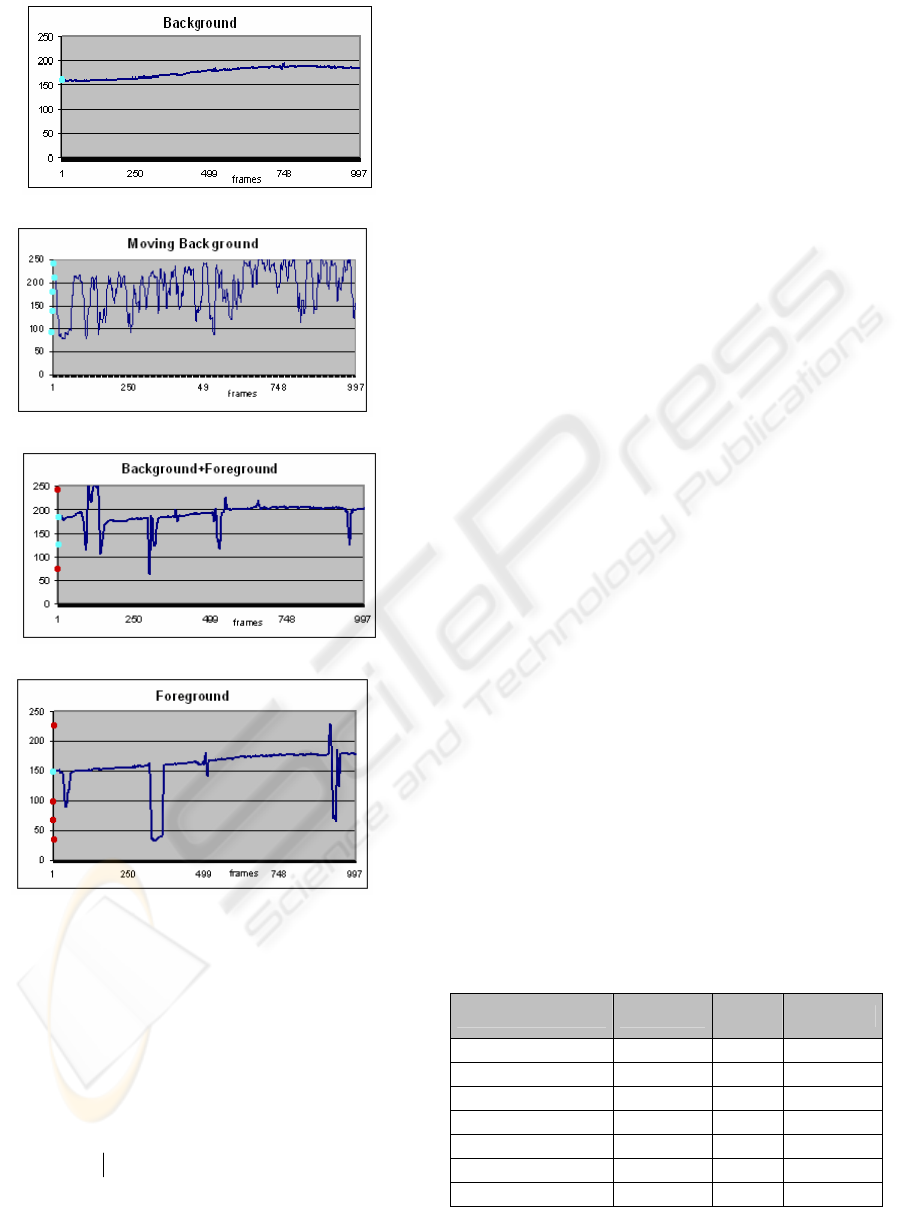
have been averaged, and in figure 2 the temporal

trend of each group of that zones is plotted.

The static points (first graph) assume values that

can be considered constant over the entire

observation period (apart from the natural light

changes). Points corresponding to static background

(last graph), but covered by a foreground object (in

this case, a person moving in the scene) assume, for

a certain period, values that differs from the standard

background value, but in an unpredictable way. On

the other hand, static points that sometimes are

covered by moving background objects (second

graph), assume values that return many times in the

whole observation period, even if they have not a

fixed frequency. In the third graph the trend of a

background point covered by both moving

background objects and foreground ones is

represented. Some values are admissible since they

return several times, while some others are

occasional, so they need to be discarded.

Starting from this assumption, the goal of this

step is to use a multilayer approach for the

modelling, with the aim of discarding layers that

correspond to variation exhibited only a few times

for a given point. Differently, layers that in the

observation period return more times will be taken

(they probably correspond to static points covered

by background moving objects).

Formally, the main idea proposed in the previous

section remains unchanged, but it is now applied to

all the background layers. The concept of mean and

standard deviation proposed in (1) and (2) become:

)1(),(),(

−

−+=

yxyx

μααμμ

(8)

)1(|),(),(|),(

−

−+−=

yxyxyx

σαμμασ

(9)

where i changes in the range (1…K), and K is the

total number of layers. Similarly, for each frame of

the examined sequence, the decision rule proposed

in (3) for the updating of the parameters becomes

thyxByxI

<− ),(),( (10)

where the notation i indicates the examined

layer. It should be noted that, initially, there is only

one layer for each point, the coarse background

model (that correspond to the first frame).

Starting from frame #2, if the condition (10) is

not verified, a new layer is created. In this way, at

the end of the observation period, for each point the

algorithm builds a statistical model given by a

serious of couple (μ,

) for each layer. The criteria

for selecting or discarding these values is based

again on the evaluation of the energy content, but

now the equation (4) is evaluated for each layer i:

),(),(),(

∫

∈

−=

yxByxIyxE (11)

Different layers are created only for those values

that occur a certain number of times in the

observation period. However, in this way both

foreground objects and moving background ones

contribute to the layer creation.

A BACKGROUND MODELLING ALGORITHM BASED ON ENERGY EVALUATION

425

Region A

Region B

Region C

Region D

Figure 2: the position of the examined regions in the

whole image (first line) and the trend observed in

these regions. Red points correspond to layers that do

not belong to the correct model, while blue points

correspond to correct background layers

In order to distinguish these two different cases,

and maintain only information about moving

background objects, the overall occurrence is

evaluated for each layer:

ilayertheofstatistics

thetoscontributethatyxWyxO

),(#),( =

(12)

(x,y) counts the number of sliding windows that

contributes to the creation of the statistic values for

the layer i. At this point, the first K layers with the

highest overall occurrences belong to the

background model, while the others are discarded.

After the examination of all the points with (12),

the background model contains only information

about the static background and moving background

objects, while layers corresponding to spot noise or

foreground objects are discarded since they occur

only in a small number of sliding windows.

The use of sliding windows allows to greatly

reduce the memory requirements; the trade-off

between goodness and hardware requirements seems

to be very interesting with respect to the others

proposed in (Monnet,2003) and (Lipton,2002).

5 EXPERIMENTAL RESULTS

We have tested the proposed algorithm on different

sequences, in different conditions, in both indoor

and outdoor environments. In table 1 the

characteristics of each test sequence are reported.

Some sequences from the CAVIAR dataset

(http://groups.inf.ed.ac.uk/vision/CAVIAR/CAVIA

RDATA1/) have also been considered.

Each sequence represents a different real

situation, and different frame rates demonstrate the

relative independency from the size of the sliding

window (in our experiments, we have chosen to use

a sliding window containing 100 frames,

independently from the considered context and the

camera frame rate).

The first test was carried out to evaluate the

number of layers necessary for a given situation. In

table 2 the mean number of layers for each context is

reported. This value is smaller for more structured

contexts (laboratory, soccer stadium), while it is

higher in generic outdoor contexts (archeological

site, CAVIAR seq. 1). The maximum number of

layers in our experiments has been fixed to 5.

Table 1: Characteristics of the test sequences.

Test Sequence Context

Frame

rate

Size

Archeological site

Outdoor

30 768X576

Laboratory

Indoor

30 532X512

Museum

Indoor

15 640X480

Soccer stadium

Outdoor

200 1600X900

Beach

Outdoor

20 720X576

CAVIAR seq. 1

Outdoor

25 384X288

CAVIAR seq. 2

Indoor

40 384X288

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

426

The presence of moving background objects in

the beach and archeological site contexts increases

the number of layers. In more controlled

environments, like the laboratory, probably the

multilayer approach can be avoided.

Table 2: the mean number of layers for each of the

examined different contexts.

Test Sequence

Mean number of

layers

Archeological site

3.12

Laboratory 1.23

Museum 2.05

Soccer Stadium 1.92

Beach 4.33

CAVIAR seq. 1 2.28

CAVIAR seq. 2 1.54

In order to have a quantitative representation of

the reliability of the background models, we have

chosen to test them by using a standard, consolidated

motion detection algorithm, proposed in

(Kanade,1998). A point will be considered as a

foreground point if it differs from the mean value

more than two times the standard deviation:

),(2),(),( yxVyxByxI

∗>−

(13)

A quantitative estimation of the error,

characterized by the Detection Rate (DR) and the

False Alarm Rate (FAR), has been used as suggested

in (Jaraba,2003):

FNTP

FAR

(14)

where TP (true positive) are the detected regions that

correspond to moving objects; FP (false positive) are

the detected regions that do not correspond to a

moving object; and FN (false negative) are moving

objects not detected. In table 3 we can see the results

obtained on the seven test sequences after a manual

segmentation of the ground truth. The FAR

parameter is always under the 6%, and it is higher

for more complex environments (i.e. beach,

museum), while it assumes small values in more

controlled contexts (i.e. soccer stadium).

We have preferred to propose our experimental

results instead of compare them with the same

obtained by others because of we consider that

implementation of algorithms of other authors can

be not perfect, so the obtained results could be

corrupted by this incorrect implementation.

As a future work, we are including the

background modelling algorithm in a complete

motion detection system, able to take advantage of

the main characteristics of the proposed algorithm.

Table 3: Rates to measure the confidence.

Test sequence DR (%) FAR (%)

Archeological site 87.46 3.72

Laboratory 93.81 4.16

Museum 89.12 4.83

Soccer stadium 94.31 2.26

Beach 88.56 5.26

CAVIAR seq. 1 89.18 3.24

CAVIAR seq. 2 91.15 3.85

REFERENCES

Wren, C.R., Azarbayejani, A., Darrell, T., Pentland, A.P.

(1997). Pfinder: real-time tracking of human body,

IEEE Trans. PAMI., 19(7), pp. 780 – 785, July.

Kanade, T., Collins, T., Lipton, A. (1998). Advances in

Cooperative Multi-Sensor Video Surveillance, Darpa

Image Und. Work., Morgan Kaufmann,pp.3-24, Nov.

Stauffer, C. and Grimson, W. (1999). Adaptive

background mixture models for real-time tracking,

Proc. of CVPR, pages II 246-252

Haritaoglu, I., Harwood, D., Davis, L.S. (1998). Ghost: A

human body part labeling system using silhouettes,

Fourteenth Int. Conf. on Patt. Rec., Brisbane, Aug.

Kim, K., Chalidabhongse, T.H., Harwood, D., Davis, L.

(2004). Background modeling and subtraction by

codebook construction, ICIP, Vol.5, pp3061–3064

Koller, D., Weber, J. and Malik, J. (2004). Robust

multiple car tracking with occlusion reasoning, ECCV

1994, pages 189-196, Stockholm, Sweden, May

Elgammal, A., Harwood, D., Davis, L.S. (2000). Non-

parametric model for background subtraction, ECCV,

Vol. 2, pp. 751-767

Doretto, G., Chiuso, A., Wu, Y.N. and Soatto, S. (2003).

Dynamic textures, IJCV, 51 (2), pp 91-109, Febr.

Monnet, A., Mittal, A., Paragios, N. and Ramesh, V.

(2003). Background modelling and subtraction of

dynamic scenes, ICCV,pp.1305-12, Nice(Fr), October

Zhong, J. and Sclaroff, S. (2003). Segmenting foreground

objects from a dynamic, textured background via a

robust kalman filter in ICCV, pp.44-50, Nice(Fr), Oct.

Toyama,K., Krumm,J., Brumitt, B. and Meyers, B. (1999).

Wallflower: Principles and practice of background

maintenance, ICCV,pp.255-61, Kerkyra(Gr), Sept.

Lipton, A.J. and Haering, N., (2002). ComMode: an

algorithm for video background modeling and object

segmentation, Proc. of ICARCV, pages 1603-08, vol.3

Jaraba, E.H., Urunuela, C. and Senar, J. (2003). Detected

motion classification with a double-background and a

Neighborhood-based difference, Pat. Recogn.

Letter,pp.2079-82 (24).

A BACKGROUND MODELLING ALGORITHM BASED ON ENERGY EVALUATION

427