
IMAGE “GROUP-REGISTRATION”
BASED ON REPRESENTATION THEORY
Lamia Ben Youssef
GRIFT, Lab. Cristal, ENSI
Campus Universitaire de la Manouba, 2010 Manouba, Tn
Faouzi Ghorbel
GRIFT, Lab. Cristal, ENSI
Campus Universitaire de la Manouba, 2010 Manouba, Tn
Keywords:
Representation theory, homogeneous space, generalized correlation, group-registration, similarities, projective
transformations.
Abstract:
The general principle of a matching algorithm is to optimize a criterion that furnishes a measure of the sim-
ilarity between two images for a given space of geometrical transformations. In this work, we propose a
framework based on a similarity measure – the generalized correlation – built in a systematic way from the
links between a features space and a group of transformations modeled by an action group.
Using results from representation theory, we can extend the correlation function to any homogeneous space
with a transitively acting group. When the generalized Fourier transform exists, the group-based correlation
can be expressed in a spectral space and it becomes possible to implement fast algorithms for its computation.
Two important examples in the field of image processing are then detailed: the similarity group (rotation
and scaling) on gray-level shapes from 2D images and the 3D rigid motion group (rotation and translation)
followed by a plan projection.
1 INTRODUCTION
Cross correlation techniques, under different names
and guises, constitute one of the most popular means
for handling with problem of motion analysis and
detection. Cross correlation is the basis for such
methods as matched filtering, modulation and phase
transfer functions, maximum likelihood type meth-
ods in statistical setting. The popularity of cross cor-
relation methods can be explained by their simplic-
ity, amenability to digital implementation, and ro-
bustness in presence of noise. Such techniques are
well known to be efficient for registration process
in the case of motions described by translation of
the plane (Brown, 1992). However, the inability of
conventional cross correlation to deal with rotation
and dilation has brought about a number of other ap-
proaches from invariant pattern recognition.
Image registration is one of the oldest and funda-
mental processing to check image similarity based
on a quantitative measure and to locate a template
at the place of its optimum value. There have been
several approaches for image registration, such as
feature-, brightness- and aggregated measure-based
ones among them color or gray-level histograms (Zi-
tov
`
a and Flusser, 2003).
Many non-brightness feature-based approaches
have been proposed to robust image matching, among
them the generalized Hough transform proposed
by (Ballard, 1981) is one of the famous meth-
ods. Another exemple is given by the indexing ap-
proaches (Y. Lamdan, 1988) that adopt combina-
tions of geometric features, such as edges or line
segments, as key for indexing objects and search-
ing them to pick up candidates. But we cannot ex-
pect a reliable matching result without some pre-
processing technics –which are subject to instability–
to detect features of interest. Moment-based ap-
proaches (S.X. Liao, 1996) and color or histogram in-
dexing methods (M.J. Swain, 1991) can be used for
rotated patterns, but they are computationally expen-
sive and not really robust in case of brightness change
and occlusion.
The correlation technics can be used to answer
these two difficulties once geometrical distortions
are integrated in the registration process. Pin-
stov (Pintsov, 1989) has suggested the use of a cross
correlation function operating with three parameters:
a picture, a template and the planar Euclidian group.
This correlation, which involves a parametric tem-
317
Ben Youssef L. and Ghorbel F. (2006).
IMAGE “GROUP-REGISTRATION” BASED ON REPRESENTATION THEORY.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 317-322
DOI: 10.5220/0001373903170322
Copyright
c
SciTePress

plate (like line, circle ...), appears to be a particu-
lar case of the well-known Radon transform. Seg-
man (Segman, 1992; Segman and Zeevi, 1993; Ru-
binstein et al., 1991) has shown that the Fourier trans-
form written with an appropriate kernel could be seen
as a cross correlation function adapted to the general
affine transformations.
In the present work, we extend Segman’s model to
more general group of transformations such as pro-
jective, non-uniform dilatation, and also to any tem-
plates, e.g. non-parametric shapes (planar or 3D ob-
jects). Based on representation theory, we propose a
framework (Ben Youssef, 2004) for studying image
deformations applicable not only in the plane but also
in other domains like the sphere. This framework in-
volves three steps:
• Identify the domain of definition of the signal as a
homogeneous space and the group acting on it.
• Check whether an invariant measure exists for the
acting group.
• Compute the transformation (group action) from
the adapted correlation.
The remaining of the paper is organized as follows.
Sec. 2 presents a short introduction to representation
theory, in particular the generalized correlation and
the convolution theorem is detailed. Sec. 3 deals with
four interesting cases for image processing, i.e. the
planar and vectorial similarity groups, the motion and
the projective groups. Several experiments on real im-
ages illustrate the different cases and confirm the nu-
merical feasibility of the methodology.
2 GROUP BASED CORRELATION
This section is not meant as a formal enumeration of
the assumptions we make. It is a rather intuitive de-
scription of what is required to apply the recipe of a
generalized Fourier transform. We assume that the
reader is familiar with the concept of group. Let us
live with an intuitive definition of a Lie group: its
elements are on smooth manifold and that the group
operation and the inversion are smooth maps (Miller
and Younes, 2001). The real line and the circle are Lie
groups with respect to addition and well known ma-
trix Lie groups are the general linear group of square
invertible matrices, the rotation groups SO(n), and
the Lorentz group.
A group G is acting on a space X when there is a
map G×X −→ X such that the identity element of the
group leaves X as is and a composition of two actions
has the same effect as the action of the composition
of two group operations (associativity). For example,
the isometry group SE(2) acts on the plane R
2
. The
rotation group SO(3) can act on the sphere S
2
. The
set of all gx ∈ X for any g ∈Gis called the orbit of
x. If the group possesses an orbit, that means for any
a, b ∈ X,ga = b for a g ∈G, then the group action
is called transitive. For example, there is always a
rotation mapping one point on the sphere to another.
If a subgroup H of G fixes a point x ∈ X then H
is called the isotropy group. A typical example of
an isotropy group is the subgroup SO(2) of SO(3)
acting on the north-pole of a sphere.
A space X with a transitive Lie group action G is
called homogeneous space. If the isotropy group is
H, it is denoted with G = H. The plane R
2
is the
homogeneous space SE(2) = SO(2). The sphere
S
2
is the homogeneous space SO(3) = SO(2). Im-
ages are usually defined on homogeneous spaces and
their deformations are the group actions. The ques-
tion is now, for which groups we can explicit a cor-
relation function and does a Fourier transform exist?
The answer requires, first, to be able to integrate on
the group and on the homogeneous space and, sec-
ond, to find the Fourier basis analogous to e
ixω
on the
real line (Miller and Younes, 2001).
We consider a simple two dimensional translation
registration problem. The classical correlation :
C(u, v)=
R
2
f(x, y) h(x − u, y − v) dxdy, (1)
is extended in a natural way to include rotations and
dilations of the template object. Essentially, we ro-
tate, and dilate the template object, overlap it with the
image and compute an overlap area (weighted by the
intensity value at each pixel) with the proper normal-
ization.
C
ex
(α, β)=
R
2
f
x
y
h
αx cos β − αy sin β
αx sin β + αy cos β
dx dy.
The function C
ex
has a maximum that will determine
the scale and the orientation of a target. One limita-
tion of this method is its incapacity to detect a ref-
erence target at different scale (Fig 1). Therefore,
we need to determine a correlation type depending on
transformation parameters.
2.1 Generalized Correlation
Function
Let L (X,dµ) denotes the set of functions which have
a mean defined as
X
|f(x)|
2
dµ(x) where µ is an in-
variant measure. The correlation of functions f
1
and
f
2
for all g ∈Gwith respect to group G is given by
(f
1
⊕ f
2
)(g)=
X
f
1
(g
−1
s)f
2
(s)χ(g)dµ(s) (2)
VISAPP 2006 - IMAGE ANALYSIS
318

(a) Butterfly im. (b) Transformed im.
(c) Correlation surface
Figure 1: Classical correlation surface.
If µ is also invariant under G, then (2) becomes
(f
1
⊕ f
2
)(g)=
X
f
1
(g
−1
s) f
2
(s)dµ(s). (3)
In this case, the correlation function has the proper-
ties:
1. The invariance of the Haar measure on X under the
transformation group G allow this following opera-
tion:
X
f
1
(g
−1
s) f
2
(s) dµ(s)=
X
f
1
(s) f
2
(gs) dµ(s)
(4)
2. If f
1
is the translated version of f
2
by g
0
with re-
spect to G, then the correlation in Eq. (3) becomes:
(f
1
⊕ f
2
)(g)=∆
g
−1
0
(f
2
⊕ f
2
)(g)(g
0
g), (5)
where ∆(g
−1
0
) is the modulus function of group G.
For Abelian group ∆(g
−1
0
)=1, then C
f
1
f
2
(g)=
C
f
2
f
2
(g
0
g) and C
f
1
f
1
(g)=C
f
2
f
2
(g).
2.2 Correlation Theorem
The correlation theorem is useful, in part because it
gives a way to simplify many calculations. Corre-
lation can be very difficult to calculate directly, but
is often much easier to calculate using Fourier trans-
forms and multiplication. The correlation theorem
can be stated in words as follows: the Fourier trans-
form of a correlation integral is equal to the product of
the complex conjugate of the Fourier transform of the
first function and the Fourier transform of the second
function.
Let G be a locally compact Abelian group with an
invariant measure dµ. The Fourier transform maps
correlation into multiplication:
F (f
1
⊕ f
2
)=F(f
1
). F
∗
(f
2
). (6)
Then generalized correlation in the Fourier domain is
given by
(f
1
⊕ f
2
)=F
−1
F(f
1
). F
∗
(f
2
)
. (7)
When generalized Fourier transform is
F
f
(λ)=
ˆ
f(λ)=
G
f(x)[T
λ
(x)] dµ(x), (8)
its inverse when exists is explicit:
f(x)=
ˆ
G
ˆ
f(λ)[T
λ
(x)]
−1
dµ(λ). (9)
3 CORRELATION ON
PARTICULAR GROUPS
The image plane X is identified with the Euclidean
space R
2
.
3.1 Planar Radial Scaling and
Angular Rotation
We first consider the group of radial dilation and
angular rotation N , group of elements (r, θ) where
r ∈ R
∗
+
and θ ∈ S
1
. It is well known that the in-
variance measure under the action of N is
dr
r
dθ. X in
polar co-ordinate system is identified to G. According
to Eq. (3), correlation of f and h ∈ L
2
R
∗
+
× S
1
for
all (α, β) ∈ R
∗
+
× S
1
is:
C
fh
(α, β)=
+∞
0
2π
0
h
r
α
,θ− β
f (r, θ)
dr
r
dθ.
(10)
Fig. 2 illustrates the correlation surface between two
images of the same object (a butterfly), but with dif-
ferent size and orientation (ρ =1.33 and θ =60
o
).
The similarity between the two images is measured
by detecting the maximum of the output correlation
given by Eq. (10). The position of this maximum
gives the parameters of the image transformation.
To calculate this correlation function, we can use
the correlation theorem for the Fourier-Mellin trans-
form (Ghorbel, 1994; Derrode and Ghorbel, 2001)
which is given by
M
f
σ
(k, v)=
1
2π
∞
0
2π
0
f(r, θ) r
iv
e
−ikθ
dθ
dr
r
.
(11)
IMAGE “GROUP-REGISTRATION” BASED ON REPRESENTATION THEORY
319
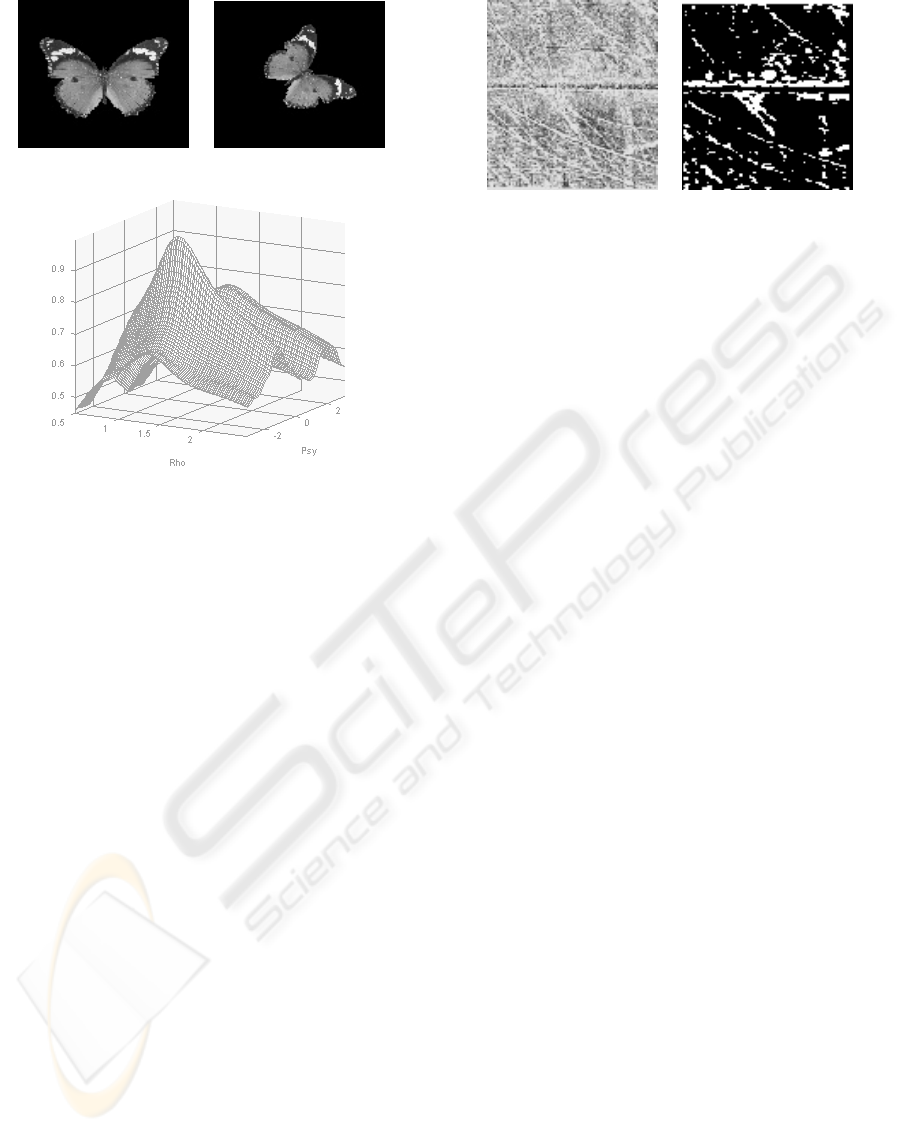
(a) Butterfly im. (b) Transformed im.
(c) Correlation surface
Figure 2: Example of a scale and rotation correlation sur-
face.
3.2 Motion Group
Let M(2) be the group of rigid motions of the plane
over R
2
, i.e. the group of elements g =(A, b) where
A ∈ SO(2) and b ∈ R
2
. Let H = SO(2) be the
transitive subgroup of M(2) over S
1
. By Mackey de-
composition theorem, every element of M(2) may be
represented in the form g =(A, b)=(I , b) · (A, 0),
with I the unitary matrix. Hence, each element of the
left coset gH may be uniquely represented by a point
x = b of the plane R
2
. We obtain the action of M(2)
on R
2
by
Ax+b =
cos θ − sin θ
− sin θ cos θ
x
1
x
2
+
b
1
b
2
.
The invariant measure on R
2
(Lebesgue measure)
is invariant under the action of rigid motions. With
respect to the lift previously defined, M(2) is a prod-
uct of R
2
by the compact space S
1
so that square sum-
mable functions with respect to the Lebesgue measure
on R
2
lift M(2) into square summable functions with
respect to the Haar measure. These two facts allow to
define the correlation function on the plane (Gauthier
et al., 1991). Therefore, for two functions f, h ∈ L
2
R
2
,dx
and for dµ(R, x)=dθdx,wehave
C
fh
(A, b)=
R
2
h(x)f (Ax + b) dx. (12)
(a) Sea floor image. (b) Trawl traces.
Figure 3: Detection of trawl traces on sonar seafloor image.
3.3 Similarity Group
We now consider the group of similarity GS, group of
elements (a, A, b) where, a ∈ R
∗
+
, A ∈ SO(2) and
b ∈ R
2
. Let N = R
∗
+
× S
1
be the transitive subgroup
of GS (see section 3.1). By Mackey decomposition
theorem, each element of GS may be represented in
the form g =(a, A, b)=(1,I,b).(a, A, 0). Hence
each element of the left coset gH may be uniquely
represented by a point x = b of the plane R
2
. The
multiplication group is given by
g
1
· g
2
=
a
1
· a
2
, (A
1
A
2
)
T
,a
1
· A
T
1
b
2
+ b
1
.
The invariant measure on A is invariant relatively
to translations and, therefore, should be proportional
to the Lebesgue measure. Such a measure cannot,
however, be invariant to homothetic transformations
x → ax and, consequently, there is no measure on A
invariant under GS. However there exists a relatively
invariant measure on the homogeneous space given
by the differential of Eq. d(gx)=J
g
.dx (J is the Ja-
cobean of g). According to Eq. (2) correlation of two
functions f and h defined on L
2
R
2
, Jdx
is
C
fh
(a, A, b)=
R
2
f (x) h (aAx + b) Jdx (13)
Fig. 3 shows a typical application of the correlation
given by Eq. (13). The goal was to identify circular
or rectilinear sand structures of variable sizes on the
sea ground. These structures come from various hu-
man activities, such as the use of explosive devices,
trawling or boat anchoring within the seagrass bed.
This correlation measure algorithm allowed to recog-
nize and detect traces of trawls independently of their
position, orientation and distance to the sonar head.
3.4 Projective Group
We begin by considering the process of image for-
mation when a scene is viewed through a camera. In
particular we will consider image formation through a
pinhole camera. A pinhole camera is a box in which
VISAPP 2006 - IMAGE ANALYSIS
320

(a) Sea floor image.
Figure 4: The pinhole imaging model.
one of the walls has been pierced to make a small hole
through it.
Assuming that the hole is indeed just a point, ex-
actly one ray from each point in the scene passes
through the pinhole and hits the wall opposite to it.
This results in an inverted image of the scene, as can
be seen in figure 4.
Let us begin by considering a mathematical de-
scription of the imaging process through this ideal-
ized camera; we will consider issues like lens distor-
tion subsequently. The pinhole camera or the projec-
tive camera images the scene by applying a perspec-
tive projection that maps the 3D space to a 2D plane.
The camera has the pinhole located at the origin and
the image plane consists of points (x
l
, 1,x
3
) identi-
fied with complex numbers x
3
+ ix
1
. Thus, the im-
age of an object is obtained by projecting the object
points into the image plane according to
x
3
+ix
1
x
2
. The
camera is embedded into the complex plane:
C
2
=
z
1
z
2
|z
1
= x
2
+ iy,z
2
= x
3
+ ix
1
(14)
Geometry of the image plane C, homogeneous un-
der the action of SL(2, C){±I} by linear-fractional
transformations, can be dually described as follows:
1. C is the complex projective line with the
group of projective transformations PSL(2, C)=
SL(2, C){±I}. Thus, the image projective
transformations acting on the points of the image
plane of the conformal camera can be identified,
with projective geometry, to the one-dimensional
complex line (Cox et al., 1996).
2. C is the Riemann sphere since, under stereographic
projection, we have the isomorphism C
∼
=
S
(0,1,0)
.
The group PSL(2, C) acting on C consists of
the bijective meromorphic mappings of C (Turski,
2004).
The following subgroup of SL(2, C) acting on the
image plane gives all basic classes of the image pro-
jective transformations of planar objects. l’eq. suiv-
ante):
SU(2) =
αβ
−
β α
||α|
2
+ |β|
2
=1
(15)
(a) Image. (b) Perspective im.
(c) Correlation surface
Figure 5: Perspective projection estimation with correla-
tion.
generates image projective transformations (with con-
formal distortions) by first rotating the projection in
the camera of an image on S
(0,1,0)
and then project-
ing it back to the image plane. This follows from the
fact that there is one-to-two correspondence between
the group of rotations S0(3) and SU(2)-the universal
double covering group of S0(3).
Or, on the sphere, we can explicit correlation for
functions defined on L
2
(S
2
)
(f
1
⊗f
2
)(g)=
S
2
f
1
(ω)f
2
(g
−1
ω)dµ(ω), (16)
where dµ(ω)=sin(θ)dθdφ is the rotation-invariant
volume measure on the sphere. The Fourier transform
also exists and is given by the spherical Fourier trans-
form:
ˆ
f(l, m)=
S
2
f(θ, φ)
¯
U
m
l
(θ, φ)sin(θ) dθdφ. (17)
Fig. 5 shows an example of image matching based on
correlation measure (16).
4 CONCLUSION
In this paper, the problem of registering two images
or recovering a template in a complex scene is for-
IMAGE “GROUP-REGISTRATION” BASED ON REPRESENTATION THEORY
321

mulated according to the generalized correlation ap-
proach. From the representation theory, we have pro-
posed a correlation function adapted to the group of
transformations and the data space when it is iden-
tified to a homogeneous space. Interesting cases for
image processing, i.e. the planar and vectorial simi-
larity groups, the motion and an interesting subgroup
projective transformations, are detailed and illustrated
with real images.
In future work, we plan to provide an in-depth
study and comparison of the algorithms behavior with
respect to robustness, computation time and achiev-
ability in real contexts. An other objective will be
to propose a correlation function on the whole group
SL(2, C), providing a way to register images for all
kinds of projective transformations.
REFERENCES
Ballard, D. (1981). Generalizing the hough transform
to detect arbitrary shapes. Pattern Recognition,
13(2):111122.
Ben Youssef, L. (2004). Corr
´
elation sur les Groupes pour
l’Analyse des Formes et l’Estimation du Mouvement,
Application aux Images Sonar. Phd thesis, Univ. de
Bordeaux 3. in french.
Brown, L. G. (1992). A survey of image registration tech-
niques. ACM Computing Surveys, 24(4):325–376.
Cox, D., Little, J., and O’Shea, D. (1996). Ideals, Vari-
eties, and Algorithms. An Introduction to Computa-
tional Algebraic Geometry and Commutative Algebra.
Springer- Verlag.
Derrode, S. and Ghorbel, F. (2001). Robust and efficient
Fourier-Mellin transform approximations for gray-
level image reconstruction and complete invariant de-
scription. Computer Vision and Image understanding,
33(1):57–78.
Gauthier, J., Bornard, G., and Silbermann, M. (1991). Mo-
tions and pattern analysis : Harmonic analysis en mo-
tion groups and their homogeneous spaces. IEEE
trans. on Systems, Man, and Cybernetics, 21(1):159–
172.
Ghorbel, F. (1994). A complete invariant description for
gray-level images by the harmonic analysis approach.
Pattern Recognition Letters, 15:1043–1051.
Miller, M. and Younes, L. (2001). Group actions, homeo-
morphisms, and matching: A general framework. J.
of Computer Vision, 41(1):6184.
M.J. Swain, D. B. (1991). Color indexing. Internat. J. Com-
put. Vision, 7(1):1132.
Pintsov, D. (1989). Invariant pattern recognition, symmetry,
and Radon transforms. J. of the Optical Society of
America A, 6(10):1544–1554.
Rubinstein, J., Segman, J., and Zeevi, Y. (1991). Recogni-
tion of distorted patterns by invariance kernels. Pat-
tern Recognition, 24(10):959–967.
Segman, J. (1992). Fourier cross correlation and invariance
transformation for an optimal recognition of functions
deformed by affine groups. J. of the Optical Society of
America A, 9:895–902.
Segman, J. and Zeevi, Y. (1993). Image analysis by wavelet-
type transforms: Group theoretic approach. Mathe-
matical Imaging and Vision, 3(1):51–77.
S.X. Liao, M. P. (1996). On image analysis by mo-
ments. IEEE Trans. Pattern Anal. Machine Intell,
18(3):254266.
Turski, J. (2004). Geometric Fourier analysis on the con-
formal camera for active vision. Society for industrial
and applied mlathematics, 46(2):230–255.
Y. Lamdan, H. W. (1988). Geometric hashing: a general
and efficient model-based recognition scheme. Proc.
ICCV, page 238249.
Zitov
`
a, B. and Flusser, J. (2003). Image registration meth-
ods: a survey. Image and Vision Computing, 21:977–
1000.
VISAPP 2006 - IMAGE ANALYSIS
322
