NEIGHBORHOOD HYPERGRAPH PARTITIONING FOR IMAGE

SEGMENTATION

Souﬁane Rital, Hocine Cheriﬁ

Facult

e des Sciences Mirande, Universit

e de Bourgogne

9, Av. Alain Savary, BP 47870, 21078 Dijon, France.

Serge Miguet

LIRIS, Universit

e Lumi

ere Lyon 2

5, avenue Pierre Mend

es France, 69500 Bron, France.

Keywords:

Graph, Hypergraph, Neighborhood hypergraph, multilevel hypergraph partitioning, image segmentation, edge

detection.

Abstract:

The aim of this paper is to introduce a multilevel neighborhood hypergraph partitioning for image segmen-

tation. Our proposed approach uses the image neighborhood hypergraph model introduced in our last works

and the algorithm of multilevel hypergraph partitioning introduced by George Karypis. To evaluate the algo-

rithm performance, experiments were carried out on a group of gray scale images. The results show that the

proposed segmentation approach ﬁnd the region properly from images as compared to image segmentation

algorithm using normalized cut criteria.

1 INTRODUCTION

Image segmentation, whose goal is the partition of

the image domain, is a long standing research subject

in computer vision (Pal and Pal, 1993). The result-

ing image subdomains, which can be denoted as im-

age segments, satisfy some condition of homogeneity,

e.g., present the same color or some kind of texture.

Image segmentation plays a principal role in the re-

alization of computer vision applications, as a previ-

ous stage for the recognition of different image ele-

ments or objects. Several algorithms have been intro-

duced to tackle this problem. It can be classiﬁed into

ﬁve approaches (Fan et al., 2001)(Navon et al., 2005),

namely: (a) Histogram-based methods, (b) boundary-

based methods, (c) region-based methods, (d) hybrid-

based methods, and (e) graph-based methods. In this

paper we brieﬂy consider some of the related work

that is most relevant to our approach: graph based

methods.

There has been signiﬁcant interest in graph-based

approaches to image segmentation in the past few

years (Wu and Leahy, 1993), (Sarkar and Boyer,

1996), (Gdalyahu et al., 2001), (Soundararajan and

Sarkar, 2001), (Shi and Malik, 2000), (Soundararajan

and Sarkar, 2003), (Wang and Siskind, 2003). The

common theme underlying these approaches is the

formulation of a weighted graph G =(X, e). The

elements in X are pixels and the weight of an edge

is some measure of the dissimilarity between the two

pixels connected by that edge (e.g., the difference in

intensity, color, motion, location or some other local

attribute). This graph is partitioned into components

in a way that minimizes some speciﬁed cost function

of the vertices in the components and/or the boundary

between those components.

Wu and Leahy (Wu and Leahy, 1993) were the ﬁrst

to introduce the general approach of segmenting im-

ages by way of optimally partitioning an undirected

graph using a global cost function. They minimized

a cost function formulated as a boundary cost met-

ric, the sum of the edge weights along a cut bound-

ary: cut(A, B)=



i∈A,j∈B

w(i, j), and with the

obvious constraints A ∪ B = X, A ∩ B = ∅, and

A = ∅, B = ∅. This cost function has a bias toward

ﬁnding small components. Cox et al. (Cox et al.,

1996) attempted to alleviate this bias by normaliz-

ing the boundary-cost metric. They proposed a cost

function, ratio regions, formulated as a ratio between

a boundary-cost metric and a segmentation-area met-

ric. Shi and Malik (Shi and Malik, 2000) and Sarkar

and Soundararajan (Soundararajan and Sarkar, 2003)

adopted different cost functions, normalized cut and

average cut, formulated as sums of two ratios between

boundary-cost and segment-area-related metrics, also

in undirected graphs.

The cost function deﬁned by Shi and Malik at-

tempts to rectify the tendency of the cut algorithm to

331

Rital S., Cheriﬁ H. and Miguet S. (2006).

NEIGHBORHOOD HYPERGRAPH PARTITIONING FOR IMAGE SEGMENTATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 331-337

DOI: 10.5220/0001376003310337

 SciTePress

prefer isolated nodes of the graph. The Normalized

cut criterion consists of minimizing:

Ncut(A, B)=

cut(A, B)

Assoc(A, X)

cut(A, B)

Assoc(B,X)

(1)

where assoc(A, X)=



i∈A,j∈B

w(i, j) which intu-

itively represents the connection cost from the nodes

in the sub-graph A to all nodes in the graph X.

An alternative to the graph cut approach is to look

for cycles in a graph embedded in the image plane. In

this case, the cost function formulated as a ratio of two

different boundary-cost metrics in a directed graph.

This cost functions can alleviate area-related biases

in appropriate circumstances. In (Wang and Siskind,

2003), Wang and Siskind present a cost function, cut

ratio, namely, the ratio of the corresponding sums of

two different weights associated with edges along the

cut boundary in an undirected graph.

In most cases, we usually want to partition (seg-

ment) an image into a larger number of parts; i.e.,

we want a k-way partitioning algorithm which divides

our image into k parts. One way of partitioning a

graph into more than two components is to recursively

bipartition the graph until some termination criterion

is met. Often, the termination criterion is based on the

same cost function that is used for bipartitioning (Shi

and Malik, 2000),(Wu and Leahy, 1993),(Wang and

Siskind, 2003). The recursive k-way partitioning al-

gorithm is time consuming because we need to apply

the same algorithm at each new iteration of the hierar-

chy. Ideally, we would like to have a direct k-way al-

gorithm which outputs the k disjoint areas in a single

iteration (Hadley et al., 1992). A common solution is

to convert the partitioning problem into a clustering

problem. Shi and Malik (Shi and Malik, 2000) deﬁne

a new criterion that can be used in a k-way algorithm.

Ncut

,...,A

cut(A

,X − A

)

Assoc(A

,X)

(2)

cut(A

,X − A

)

Assoc(A

,X)

+ ...+

cut(A

,X − A

)

Assoc(A

,X)

where A

is the ith sub-graph of G. Tal and Malik

(Tal and Malik, 2001) used the k-means algorithm

to ﬁnd a pre-selected number of clusters within the

space spanned by the non-zero, smallest e eigenvec-

tors. For those cases where the number of clusters is

not known, the authors proposed using several values

of k and then selecting that k which minimized the

criterion:

Ncut

,...,A

)/k

. (3)

In (Martinez et al., 2004), Aleix M. Martinez et al.

investigate in the other approaches to non-parametric

clustering in the eigenspace of the afﬁnity matrix.

The authors use the method of Koontz and Fukunaga

(Koontz and Fukunaga, 1972) that has the advantage

of automatically determining the optimal value of k

as the data are grouped into clusters.

The main drawback of proximity graphs is their

use of binary neighborhood relations. An image is

an organization of objects in a space, and the appro-

priate relational algebra is not necessarily a binary

one. The corresponding representation for images

data with higher order relationship is a hypergraph.

By regarding each set as a generalized edge one ob-

tains a structure called a hypergraph (Fig. 1). Sim-

ilarly to graphs, hypergraphs can be used to repre-

sent the structure of many applications, such as data

dependencies in distributed databases (Koyutrk and

Aykanat, 2005), component connectivity in VLSI cir-

cuits (Karypis et al., 1999) and image analysis (Rital

et al., 2001) (Rital and Cheriﬁ, 2004).

Vertices

edges

Ex6

(a) (b)

Figure 1: An example of (a) graph and (b) hypergraph.

Also, like graphs, hypergraphs may be partitioned

such that a cut metric is minimized. The most ex-

tensive and large scale use of hypergraph partition-

ing algorithms, however, occurs in the ﬁeld of VLSI

design and synthesis. A typical application involves

the partitioning of large circuits into k equally sized

parts in a manner that minimizes the connectivity be-

tween the parts. The circuit elements are the vertices

of the hypergraph and the nets that connect these cir-

cuit elements are the hyperedges (Alpert and Kahng,

1995). The leading tools for partitioning these hy-

pergraphs are based on two phase multi-level ap-

proaches (Karypis et al., 1999). In the ﬁrst phase,

they construct a hierarchy of hypergraphs by incre-

mentally collapsing the hyperedges of the original hy-

pergraph according to some measure of homogene-

ity. In the second phase, starting from a partition-

ing of the hypergraph at the coarsest level, the al-

gorithm works its way down the hierarchy and at

each stage the partitioning at the level above serves

as an initialization for a vertex swap based heuris-

tic that reﬁnes the partitioning greedily (Fiduccia and

Mattheyses, 1982),(Kernighan and Lin., 1970). The

development of these tools is almost entirely heuris-

tic and very little theoretical work exists that analyzes

their performance beyond empirical benchmarks. Hy-

pergraph cut metrics provide a more accurate model

VISAPP 2006 - IMAGE ANALYSIS

332

than graph partitioning in many cases of practical

interest. For example, in the row-wise decompo-

sition of a sparse matrix for parallel matrix-vector

multiplication, a hypergraph model provides an ex-

act measure of communication cost, whereas a graph

model can only provide an upper bound (Trifunovic

and Knottenbelt, 2004a) (Catalyurek and Aykanat.,

1999). It has been shown that, in general, there does

not exist a graph model that correctly represents the

cut properties of the corresponding hypergraph (Ih-

ler et al., 1993). Recently, several serial and parallel

hypergraph partitioning techniques have been exten-

sively studied (Sanchis, 1989) (Trifunovic and Knot-

tenbelt, 2004a)(Karypis, 2002) and tools support ex-

ists (e.g. hMETIS (Karypis and Kumar, 1998), PaToH

(Catalyurek and Aykanat., 1999) and Parkway (Tri-

funovic and Knottenbelt, 2004b)). These partitioning

techniques showed a very great efﬁciency in distrib-

uted databases and VLSI circuits ﬁelds.

In this paper, we widen the application area of hy-

pergraph partitioning algorithms to image ﬁelds and

more particularly to the image segmentation. The ba-

sic idea of this algorithm can be described as follows

and summarize in two steps:

1. It ﬁrst builds a hypergraph of the image.

2. Then the algorithm partitions this representation

into a set of vertices, representing homogeneous re-

gions.

The aim of the ﬁrst step is to capture all global

and local properties of the image data and the whole

key information for the segmentation purpose. This

model has proved to be extremely useful for solving

some applications in image processing ﬁelds such as

noise removal (Rital et al., 2001) and edge detection

(Rital and Cheriﬁ, 2004). While the second step of

the proposed approach partition this representation to

a homogenous regions. It is done by a fast multilevel

programming algorithm. Throughout this paper, we

will denote the hypergraph of the image by the Image

Neighborhood Hypergraph INH.

In section 2, we brieﬂy review some background on

hypergraph theory. The proposed segmentation ap-

proach is presented in Section 3 and its performance

is illustrated in Section 4. The paper ends with a con-

clusion in Section 5.

2 BACKGROUND

Our main interest in this paper is to use combinatorial

models. We will introduce basic tools that are needed.

A hypergraph H on a set X is a family (E

)

i∈I

non-empty subsets of X called hyperedges with:



i∈I

= X, I = {1, 2,...,n},n∈ N.

Given a graph G(X; e), the hypergraph having the

vertices of G as vertices and the neighborhood of

these vertices as hyperedges (including these vertices)

is called the neighborhood hypergraph of G. To each

graph we can associate a neighborhood hypergraph :

=(X, (E

= {x}∪Γ(x))) (4)

where Γ(x)={y ∈ X, (x, y) ∈ e}.

2.1 Multilevel Hypergraph

Partitioning

The goal of the k-way hypergraph partitioning prob-

lem is to partition the vertices of the hypergraph into

k disjoint subsets X

,(i =0,...,k − 1), such that

a certain objective functions deﬁned over the hyper-

edges is optimized.

Let us note H(X, E) a hypergraph. We will as-

sume that each vertex and hyperedge has a weight

associated with it, and we will use w(x) to denote

the weight of a vertex x, and w(E) to denote the

weight of a hyperedge E. One of the most com-

monly used objective functions is to minimize the

hyperedge-cut of the partitioning; i.e., the sum of the

weights of the hyperedges that span multiple parti-

tions: cut{A, B} =



∈A,E

∈B

w(E

),A,B

are two partitions. Another objective that is often used

is to minimize the sum of external degrees (SOED) of

all hyperedges that span multiple partitions (Karypis

et al., 1999).

The most commonly used approach for computing

a k-way partitioning is based on recursive bisection.

In this approach, the overall k-way partitioning is ob-

tained by initially bisecting the hypergraph to obtain a

two-way partitioning. Then, each of these parts is fur-

ther bisected to obtain a four-way partitioning, and so

on. The problem of computing an optimal bisection of

a hypergraph is at least NP-hard (Garey and Johnson,

1979); however, many heuristic algorithms have been

developed. The survey by Alpert and Kahng (Alpert

and Kahng, 1995) provides a detailed description and

comparison of various such schemes.

The key idea behind the multilevel approach for

hypergraph partitioning is fairly simple and straight-

forward. Multilevel partitioning algorithm, instead of

trying to compute the partitioning directly in the orig-

inal hypergraph, partition the hypergraph using three

process (Fig.2):

Coarsening phase: ﬁrst obtain a sequence of suc-

cessive approximations of the original hypergraph.

Each one of these approximations represents a prob-

lem whose size is smaller than the size of the origi-

nal hypergraph. This process continues until a level

of approximation is reached in which the hypergraph

contains only a few tens of vertices (Fig. 3).

NEIGHBORHOOD HYPERGRAPH PARTITIONING FOR IMAGE SEGMENTATION

333

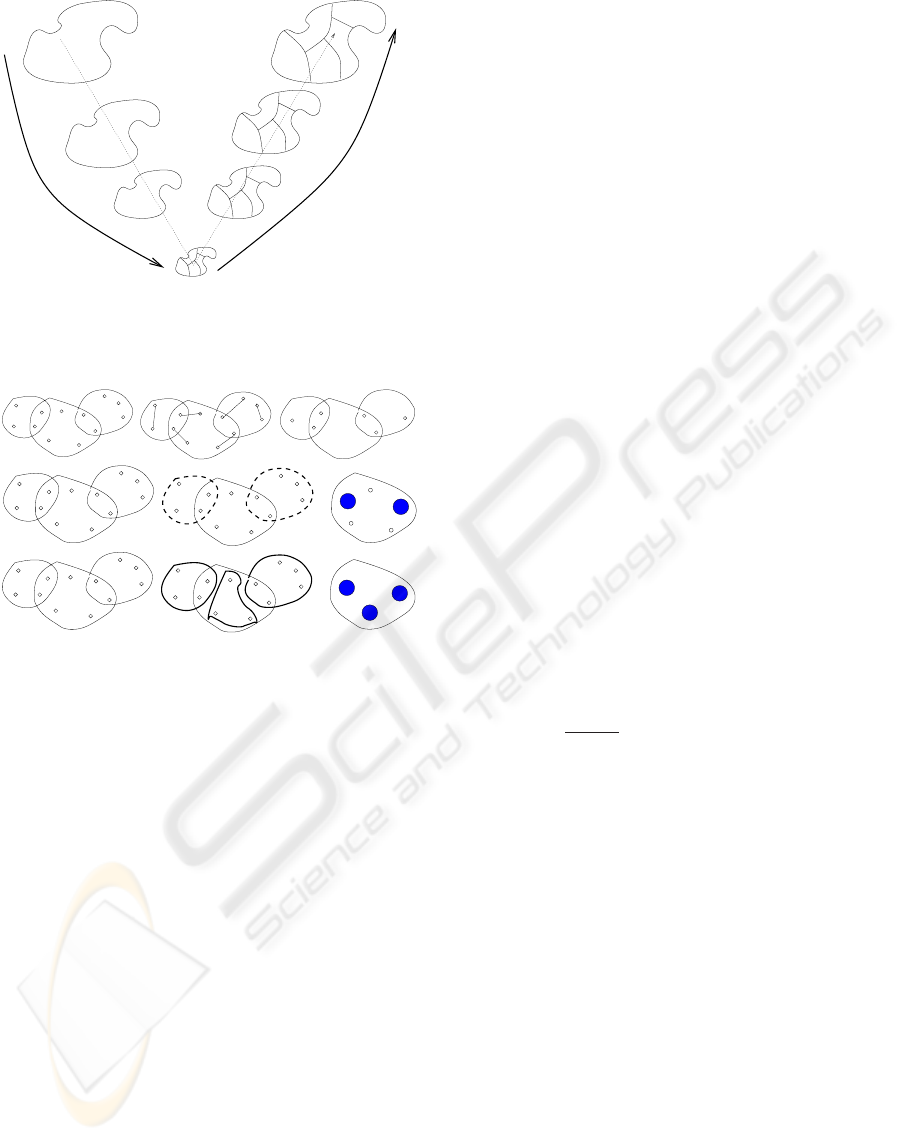
Coarsening Phase

Initial Partitioning Phase

UnCoarsening Phase

Figure 2: Multilevel Hypergraph Partitioning.

Figure 3: Some coarsening schemes: (a)Edge Coarsening,

(b) Hyperedge Coarsening, and (c) Modiﬁed Hyperedge

Coarsening.

Initial partitioning phase: At this point, these al-

gorithms compute a partitioning of that hypergraph.

Since the size of this hypergraph is quite small,

even simple algorithms such as Kernighan-Lin (KL)

(Kernighan and Lin., 1970) or Fiduccia-Mattheyses

(FM) (Fiduccia and Mattheyses, 1982) lead to reason-

ably good solutions. Uncoarsening phase: ﬁnal step

of these algorithms is to take the partitioning com-

puted at the smallest hypergraph and use it to derive

a partitioning of the original hypergraph. This is usu-

ally done by propagating the solution through the suc-

cessive better approximations of the hypergraph and

using simple approaches to further reﬁne the solution.

2.2 Image and Neighborhood

Relations

In this paper, the image will be represented by the

following mapping : I : X ⊆ Z

−→ C ⊆ Z

. Ver-

tices of X are called pixels, elements of C are called

colors. A distance d on X deﬁnes a grid (a connected,

regular graph , without both loop and multi-edge). Let



be a distance on C, we have a neighborhood rela-

tion on an image deﬁned by :

∀x ∈ X, Γ

λ,β

(x)={x



∈ X, x



= x | (5)



(I(x),I(x



) ≤ λandd(x, x



) ≤ β)

The neighborhood of x on the grid will be denoted

by Γ

λ,β

(x). To each image we can associate a hyper-

graph called Image Neighborhood Hypergraph (INH)

(Rital and Cheriﬁ, 2004):

λ,β

=(X, ({x}∪Γ

λ,β

(x))

x∈X

). (6)

On a grid Γ

, to each pixel x we can associate a neigh-

borhood Γ

λ,β

(x), according to a predicate λ. The

predicate λ may be completely arbitrary, it is useful

for a task domain. It may be deﬁned on a set of points,

it may use colors, or some symbolic representation of

a set of colors, or it may be a combination of several

predicates, etc.

From H

λ,β

, we deﬁne a weighted image neighbor-

hood hypergraph (WINH) according to the two maps

functions f

and f

. The ﬁrst map f

, associates

an integer weight w

with every vertex x

∈ X. The

weight is deﬁned by the color in each pixel. The map

function f

associates to each hyperedge a weight

deﬁned by the mean color in hyperedge. The

WINH is deﬁned by :

λ,β

=(X, E

λ,β

), (7)

∀x ∈ X, f

(x)=I(x)

∀E(x) ∈ E

λ,β

(E(x)) = (8)

|E(x)|



i=1

I(x

)

∈E(x)

3 SEGMENTATION ALGORITHM

In this section, we describe a segmentation algorithm

based on image neighborhood hypergraph represen-

tation and multilevel hypergraph partitioning method.

It starts with a WINH generation followed by a mul-

tilevel hypergraph partitioning. The steps of the algo-

rithm are described below :

1. Input : Image, thresholds λ, β and µ (the number

of regions).

2. Weighted Image Neighborhood Hypergraph

(WINH) generation.

3. Multilevel weighted image neighborhood hyper-

graph partitioning

(a) the coarsening phase

(b) the initial partitioning

4. Output : segmented Image.

VISAPP 2006 - IMAGE ANALYSIS

334

(a) (b)

(c)

Figure 4: The output of the proposed algorithm with WINH

(a) using weighted vertices only, (b) using weighted hyper-

edge only, (c) using weighted both vertices and hyperedges.

The parameters algorithm :β =1, λ =15and µ =51.

4 EXPERIMENTAL RESULTS

A group of a gray scale images with different ho-

mogenous areas were chosen in order to demonstrate

the performances of the proposed algorithm. First, we

build the WINH. The values of β, λ and µ are adjusted

in experiments. The values posted thereafter corre-

sponds to the best results. In the coarsening phase of

the second part of the proposed algorithm, we use the

hyperedge coarsening method (Fig. 3).

During the initial partitioning phase, a bisection

of the coarsened image neighborhood hypergraph is

computed. We use multiple random bisections, fol-

lowed by the Fiduccia-Mattheyses(FM) reﬁnement

algorithm. In the last phase (uncoarsening), the par-

titioning is done by successively projecting the parti-

tioning to the next level ﬁner WINH and using a par-

titioning reﬁnement algorithm to reduce the cut and

thus to improve the quality of the partitioning. For

this phase, we use the reﬁnement algorithm integrated

in HMETIS package (Karypis and Kumar, 1998).

We ﬁrst evaluate the performance of the proposed

algorithm using WINH. In this experiment, we want

to know the best WINH representation allowing to

improve the next stage of algorithm (hypergraph

partitioning) and consequently the segmentation ap-

proach. We implement the algorithm with three types

of WINH : (1) using weighted vertices only, (2) us-

ing weighted hyperedges only and (3) using weighted

both vertices and hyperedges. Figure 4 shows the re-

(a)

(b) µ =51, λ =15, β =1and computing time

= 32.23s

Figure 5: A comparison between the proposed algorithm

and normalized cut. (a) the original image. (b) the output

of the proposed algorithm. (c) the output of normalized cut

algorithm.

sults of the proposed algorithm using these three types

of WINH. We can see that the last representation

WINH (using both weighted vertices and weighted

hyperedges) gives signiﬁcant results; especially in the

image areas containing many information. Indeed,

the third WINH gives more information about the im-

age to neighborhood hypergraph partitioning.

In order to compare our method with an existing

one, we have chosen the technique of Malik et al. (Shi

and Malik, 2000). We have processed a group of im-

ages with our segmentation method and compared the

results to normalized cuts. Normalized cuts used the

same parameters for all images, namely, the optimal

parameters given by authors.

Figure 5 shows a comparison between our algo-

rithm and normalized cut on Peppers image. Accord-

ing to the segmentation results on this image, we note

that the proposed algorithm localize better the areas of

NEIGHBORHOOD HYPERGRAPH PARTITIONING FOR IMAGE SEGMENTATION

335

(a) µ =35, λ =11, β =1

(b) µ =23, λ =15, β =1

(d) µ =58, λ =21, β =1

(e) µ =27, λ =15, β =1

Figure 6: The outputs of the proposed algorithm on other

images. (a),(b),(c) and (d) the original images.

the treated image that the normalized cut algorithm.

Figure 6 shows the results of the proposed algorithm

on other images.

The strength of our algorithm is that it better de-

tects the regions containing many details. In addition,

our algorithm is powerful in computing times. It is

ten times inferior comparing to normalized cuts algo-

rithm.

5 CONCLUSIONS

We have presented a weighted image neighborhood

hypergraph partitioning for image segmentation. The

segmentation is accomplished in two stages. In the

ﬁrst stage, weighted image neighborhood hypergraph

is generated. In the second stage, hypergraph parti-

tioning method using HMETIS package is computed.

Experimental results demonstrate that our approach

performs better than Normalized cut algorithm. Our

algorithm represents the ﬁrst proposition for solving

the image segmentation problem. It can be improved

in several ways (parameters : the function maps, the

colorimetric threshold, the unsupervised region num-

ber, etc.).

REFERENCES

Alpert, C. J. and Kahng, A. B. (1995). Recent developments

in netlist partitioning: A survey. Integration: the VLSI

Journal, 19(1-2):1–81.

Catalyurek, U. and Aykanat., C. (1999). Hypergraph-

partitioning-based decomposition for parallel sparse-

matrix vector multiplication. IEEE Transactions on

Parallel and Distributed Systems, 10(7):673–693.

Cox, I., Rao, S., and Zhong, Y. (1996). Ratio regions: A

technique for image segmentation. In 13th Interna-

tional Conference on Pattern Recognition (ICPR’96).

Fan, J., Yau, D. K., Elmagarmid, A. K., and Aref, W. G.

(2001). Automatic image segmentation by integrating

color edge detection and seeded region growing. IEEE

Trans. on Image Processing., 10(10):1454–1466.

Fiduccia, C. M. and Mattheyses, R. M. (1982). A linear-

time heuristic for improving network partitions. In

Proceedings of the 19th ACM/IEEE Design Automa-

tion Conference DAC 82, pages 175–181.

Garey, M. and Johnson, D. (1979). Computers and

Intractability: A Guide to the Theory of NP-

Completeness. W.H. Freeman and Co.

Gdalyahu, Y., Weinshall, D., and Werman, M. (2001). Self-

organization in vision : stochastic clustering for image

segmentation, perceptual grouping, and image data-

base organization. IEEE Trans. Pattern Anal. Mach.

Intell., 23(10):1053–1074.

Hadley, S., Mark, B., and Vannelli, A. (1992). An ef-

ﬁcient eigenvector approach for ﬁnding netlist parti-

tions. IEEE Trans. CAD, 11:885–892.

VISAPP 2006 - IMAGE ANALYSIS

336

Ihler, E., Wagner, D., and Wagner, F. (1993). Modeling hy-

pergraphs by graphs with the same mincut properties.

Inf. Process. Lett., 45(4):171–175.

Karypis, G. (2002). Multilevel hypergraph partitioning.

Technical report #02-25, University of Minnesota.

Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S.

(1999). Multilevel hypergraph partitioning: applica-

tions in vlsi domain. IEEE Trans. Very Large Scale

Integr. Syst., 7(1):69–79.

Karypis, G. and Kumar, V. (1998). hmetis 1.5: A hy-

pergraph partitioning package. Technical report,

University of Minnesota, Available onhttp://www-

users.cs.umn.edu/∼karypis/metis/hmetis/index.html.

Kernighan, B. W. and Lin., S. (1970). An efﬁcient heuris-

tic procedure for partitioning graphs. The Bell system

technical journal, 49(1):291–307.

Koontz, W. and Fukunaga, K. (1972). A nonparametric

valley-seeking technique for cluster analysis. IEEE

Trans. Comput., 21:171–178.

Koyutrk, M. and Aykanat, C. (2005). Iterative-

improvement-based declustering heuristics for multi-

disk databases. Information Systems, 30(1):47–70.

Martinez, A. M., Mittrapiyanuruk, P., and Kak, A. C.

(2004). On combining graph-partitioning with non-

parametric clustering for image segmentation. Com-

puter Vision and Image Understanding, 95:72–85.

Navon, E., Miller, O., and Averbuch, A. (2005). Color im-

age segmentation based on adaptive local thresholds.

Image Vision Comput., 23(1):69–85.

Pal, N. and Pal, S. (1993). A review on image segmentation

techniques. Pattern Recognition, 26:1277–1294.

Rital, S., Bretto, A., Aboutajdine, D., and Cheriﬁ, H.

(2001). Application of adaptive hypergraph model to

impulsive noise detection. Lecture Notes in Computer

Science, 2124:555–562.

Rital, S. and Cheriﬁ, H. (2004). A combinatorial color

edge detector. Lecture Notes in Computer Science,

3212:289–297.

Sanchis, L. A. (1989). Multiple-way network partitioning.

IEEE Transactions on Computers, pages 62–81.

Sarkar, S. and Boyer, K. (1996). Quantitative measures

of change based on feature organization: eigenvalues

and eigenvectors. Proc. IEEE Conf. Comput. Vis. Patt.

Recogn., pages 478–483.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. IEEE Transactions on Pattern Analysis

and Machine Intellignece, 22(8):888–905.

Soundararajan, P. and Sarkar, S. (2001). Analysis of min-

cut, average cut, and normalized cut measures. Proc.

Third Workshop Perceptual Organization in Computer

Vision.

Soundararajan, P. and Sarkar, S. (2003). An in-depth study

of graph partitioning measures for perceptual orga-

nization. IEEE Trans. Pattern Anal. Mach. Intell.,

25(6):642–660.

Tal, D. and Malik, J. (2001). Combining color, texture and

contour cues for image segmentation. Preprint.

Trifunovic, A. and Knottenbelt, W.(2004a). A parallel algo-

rithm for multilevel k-way hypergraph partitioning. In

Proceedings of 3rd International Symposium on Par-

allel and Distributed Computing.

Trifunovic, A. and Knottenbelt, W. (2004b). Parkway

2.0: A parallel multilevel hypergraph partitioning

tool. In Proceedings of 19th International Symposium

on Computer and Information Sciences (ISCIS 2004),

volume 3280, pages 789–800.

Wang, S. and Siskind, J. M. (2003). Image segmentation

with ratio cut - supplemental material. IEEE Trans.

Pattern Anal. Mach. Intell., 25(6):675–690.

Wu, Z. and Leahy, R. (1993). An optimal graph theoretical

approach to data clustering: theory and its application

to image segmentation. IEEE Trans. Patt. Anal. Mach.

Intell., 15:1101–1113.

NEIGHBORHOOD HYPERGRAPH PARTITIONING FOR IMAGE SEGMENTATION

337