
MINIMAL DISTORTION MAPPINGS OF SURFACES FOR
MEDICAL IMAGES
Eli Appleboim, Emil Saucan and Yehoshua Y. Zeevi
Technion, Department of Electrical Engineering
Haifa, Israel
Keywords:
medical imaging, flattening, quasi conformal maps, length distortion, angle dilatation.
Abstract:
In this paper we present a simple method for minimal distortion development of triangulated surfaces for
colon mapping and general analysis of medical images. The method is based on classical results of Gehring
and V
¨
aisal
¨
a regarding the existence of quasi-comformal and quasi-isometric mappings between Riemannian
manifolds. Random and curvature based variations of the algorithm are presented. In addition the algorithm
enables the user to compute the maximal distortion errors. The algorithm was tested both on synthetic images
of the human skull and on real CT images of the human colon.
1 INTRODUCTION
Two-dimensional representation by flattening of
three-dimensional object scans are of paramount im-
portance, in many medical applications of image
processing, such as medical imaging for noninvasive
diagnosis and image guided surgery. For example,
it is often advantageous to present three-dimensional
MRI or CT scans of the cortex as flat two-dimensional
images. Yet in order to do so in a meaningful manner,
so that the diagnosis will be accurate, it is essential
that the geometric distortion, in terms of change of
angles and lengths, caused by this representation, will
be minimal. However, since usually the studied sur-
faces is not isometric to the plane, a zero-distortion
solution is seldom feasible. Yet, a reasonable solution
to this problem is given by conformal maps (Haker
et. al., 2000a), (Haker et. al., 2000b). Mapping the
surface conformally to the (complex) plane preserves
angles and therefore the local shape. Since this cannot
be achieved in a global way, all solutions are local.
In spite of previous claims, flattening by means of
conformal mapping is practically not possible, par-
ticularly so for highly folded surfaces, such as the
colon and the cortex. Hence some distortion should
be expected in cases encountered in medical imaging.
Therefore, one should expect to obtain, some bounded
amount of distortion. This can be achieved by quasi-
isometric/quasi-conformal maps (i.e. maps that are
almost isometries/conformal; precise definition will
follow in Section 3). Practically, there is a tradeoff
between the cost of an implementation on one hand
and accuracy on the other. Common to all solutions is
the fact, which cannot be avoided because of the in-
evitable distortion, that the more locally one is willing
to focus, the more accurate the results become.
2 RELATED STUDIES
Previously-published approaches to the problem of
minimal distortion flattening of surfaces can be sorted
into three categories:
2.1 Variational Methods
Haker et al., (Haker et. al., 2000a), (Haker et. al.,
2000b) S. introduced the application of a variational
method in conformal flattening of CT and MRI 3-D
scans of the brain and colon for the purpose of med-
ical imaging. The method is essentially done by solv-
ing Dirichlet problem for the Laplace-Beltrami op-
erator u =0on a given surface Σ, with certain
(Dirichlet) boundary conditions on ∂Σ. A solution
to this problem is a harmonic (thus conformal) map
from the surface to the (complex) plane. The solution
presented in (Haker et. al., 2000a) and (Haker et.
al., 2000b) is a piecewise linear (PL) approximation
of the smooth solution, achieved by solving a proper
system of linear equations.
422
Appleboim E., Saucan E. and Y. Zeevi Y. (2006).
MINIMAL DISTORTION MAPPINGS OF SURFACES FOR MEDICAL IMAGES.
In Proceedings of the First Inter national Conference on Computer Vision Theory and Applications, pages 422-427
DOI: 10.5220/0001376204220427
Copyright
c
SciTePress

2.2 Circle Packing
In (Hurdal et. al., 1999) Hurdal a method of build-
ing such a conformal map using circle packing is sug-
gested. This relies on the ability to approximate con-
formal structure on surfaces by circle packings. The
authors use this method for MRI brain images and
conformally map them to the three possible models
of geometry in dimension 2 (i.e. the 2-sphere, the
Euclidian plane and the hyperbolic plane). Yet, the
method is applicable for a surface which are topolog-
ically equivalent to a disk whereas the brain cortex
surface is not. This means that there is a point of the
brain (actually a neighborhood of a point), which will
not map conformally to the plane, and in this neigh-
borhood the dilatation will be infinitely large. More-
over, it must be assumed that the surface triangulation
is homogeneous in the sense that all triangles are equi-
lateral. Such triangulations are seldom attainable.
2.3 Holomorphic 1-forms
Gu et al. ( (Gu, X. and Yau, S. T., 2002) and a series of
consequent papers), are using holomorphic 1-forms
in order to compute global conformal structure of a
smooth surface of arbitrary genus and arbitrary num-
ber of boundary components. Holomorphic 1-forms
are differential forms that depict conformal structure.
As such, this method can be applied to colon unfold-
ing. Yet, implementation of this method is extremely
time consuming.
2.4 Angle Methods
Sheffer et al. (Sheffer, A. de Stuler, E. ) parameterize
surfaces via an angle-based method that minimizes,
in a way, angle distortion while flattening. However,
the surfaces are assumed to be approximated by cone
surfaces i.e. one considers surfaces that are composed
of cone-like neighborhoods.
2.5 The Proposed Method
We propose yet another solution to the problem of sur-
face unfolding, with a special focus on its applications
in medical imaging. The method proposed herein is
based on theoretical results obtained by Gehring and
V
¨
aisal
¨
a in the 1960‘s and refereed to in (Gehring-
V
¨
aisala, 1965). Gehring and V
¨
aisal
¨
a investigated the
existence of quasi-conformal maps between Riemann
manifolds. The basic advantages of the proposed
method is its simplicity. It is straightforward to im-
plement this method and it is computationally effi-
cient. An additional advantage is that it is possible
to guarantee that the distortion will not exceed a pre-
defined bound, which can be as small as desired with
respect to the extent of localization one is ready to ac-
cept. Moreover, since, in contrast to other methods,
the algorithm makes no use to derivatives, it is highly
suitable for analysis of noisy data and for the study
of surfaces with folds and ridges, such as the colon
wall and the cortex. The proposed algorithm is most
able in cases where the surface is complex (high and
non-constant curvature) such as colon wrapping.
The paper is organized as follows: In the next sec-
tion we provide a review of related works. In Sec-
tion 3 some theoretical background to the fundamen-
tal work of Gehring and V
¨
aisal
¨
a. In the following sec-
tion we describe our algorithm for surface flattening,
based on their ideas. In Section 5 we present some
experimental results of this scheme and in Section 6
we summarize the paper and discuss further improve-
ments.
3 THEORETICAL BACKGROUND
Definition 1 Let D ⊂ R
3
be a domain. A homeo-
morphism f : D → R
3
is called a quasi-isometry (or
a bi-Lipschitz mapping), iff
1
C
|p
1
− p
2
|≤|f(p
1
) −
f(p
2
)| <C|p
1
−p
2
| , for all p
1
,p
2
∈ D; 1 ≤ C<∞.
C(f ) = min{C | f is a quasi − isometry} is called
the minimal distortion of f (in D). (The distances
considered are the induced intrinsic distances on the
surfaces.)
If f is a quasi-isometry then K
I
(f) ≤ C(f )
2
and
K
O
(f) ≤ C(f)
2
, where K
I
(f) and K
O
(f) repre-
sent the inner and outer dilatation of f , respectively
(see (Caraman, P., 1974) and references therein). It
follows that any quasi-isometry is a quasi-conformal
mapping (while, evidently, not every quasi-conformal
mapping is a quasi-isometry). Quasi-conformal is the
same as quasi-isometry where distances are replaced
by inner products between tangent vectors.
Definition 2 Let S ⊂ R
3
be a connected surface. S
is called admissible iff for any p ∈ S, there exists a
quasi-isometry i
p
such that for any ε>0 there exists
a neighbourhood U
p
⊂ R
3
of p, such that i
p
: U
p
→
R
3
and i
p
(S∩U
p
)=D
p
⊂ R
2
, where D
p
is a domain
and such that C(i
p
) satisfies: (i)sup
p∈S
C(i
p
) < ∞
and (ii)sup
p∈S
C(i
p
) < 1+ε .
Let S be a surface, n be a fixed unitary vector, and
p ∈ S, such that there exists a neighbourhood V ⊂ S,
such that V D
2
, where D
2
= {x ∈ R
2
||x|| ≤ 1}.
Moreover, suppose that for any q
1
,q
2
∈ S, the acute
angle (q
1
q
2
,n) ≥ α. We refer to the last condition
as the Geometric Condition or Gehring Condition.
Then for any x ∈ V there is a unique representation
of the form: x = q
x
+ un, where q
x
lies on the plane
through p which is orthogonal to n and u ∈ R.We
MINIMAL DISTORTION MAPPINGS OF SURFACES FOR MEDICAL IMAGES
423
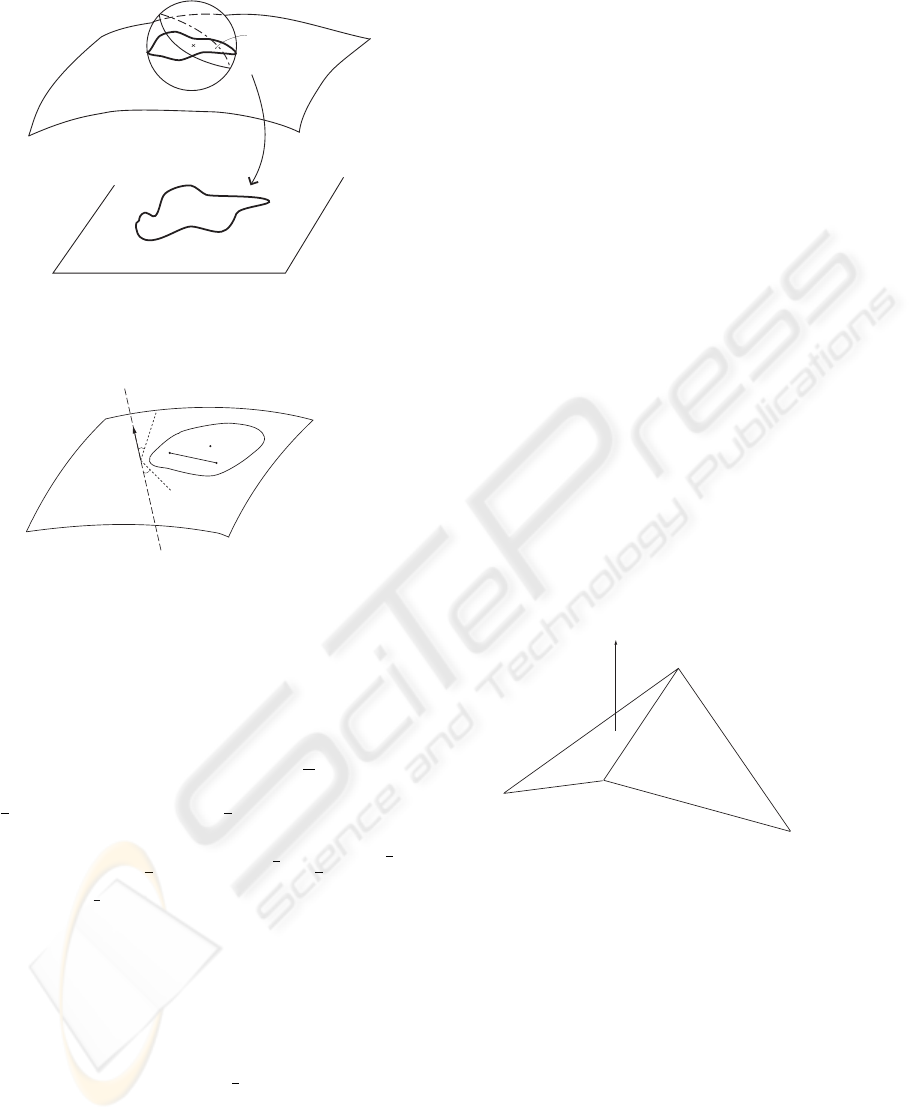
S
R
2
p
U
U S
U
p
i(p)
Figure 1: An Admissible Surface.
S
p
n
_
α
α
V S
U
~
_
D
q
q
1
2
2
Figure 2: The Geometric Condition.
define: Pr(x)=q
x
. (Note that n need not be the
normal vector to S at p.)
We have that for any p
1
,p
2
∈ S and any a ∈
R
+
the following inequalities hold:
a
A
|p
1
− p
2
|≤
|Pr(p
1
) − Pr(p
2
)|≤A|p
1
− p
2
|, where A =
1
2
[(a csc α)
2
+2a +1]
2
+
1
2
[(a csc α)
2
− 2a +1]
2
.
In particular for a =1we get that C(f) ≤ cot α +1
and K(f ) ≤
1
2
(cot α)
2
+4
1
2
+
1
2
cot α
3
2
≤
(cot α +1)
3
2
; where K(f) = max
K
O
(f),K
I
(f)
is the maximal dilatation of f. We have thus obtained:
Theorem 1 (a) The quasi-isometric projection, Pr,
yields a minimally distorted flat surface. (b) C(f) and
maximal dilatation K(f ): C(f ) ≤ cot α +1.
(b) The maximal dilatation, K(f), and
distortion, C(f), are bounded according to the fol-
lowing: K(f ) ≤ (cot α +1)
3
2
.
From the discussion above we conclude that S ⊂
R
3
is an admissible surface if for any p ∈ S there
exists n
p
such that, for any q
1
,q
2
∈ U
p
close enough
to p, the acute angle (q
1
q
2
,n
p
) ≥ α. In particular,
any smooth surface in S ∈ R
3
is admissible.
3.1 The Algorithm
We proceed to present the algorithm that is used for
obtaining a quasi-isometric (flat) representation of a
given surface.
Assume that the surface is equipped with some tri-
angulation T . Let N
p
stand for the normal vector to
the surface at a point p on the surface.
A triangle ∆, of the triangulation must be chosen.
We project a patch of the surface quasi-isometrically
onto the plane included in ∆. This patch is called the
patch of ∆, and it consists of at least one triangle, ∆
itself. There are two possibilities to chose ∆, one is in
a random manner and the other is based on curvature
considerations. We will refer to both ways later. For
the moment, assume ∆ was somehow chosen. Af-
ter ∆ is (trivially) projected onto itself we move to
its neighbors. Suppose ∆
is a neighbor of ∆ having
edges e
1
, e
2
, e
3
, where e
1
is the edge common to both
∆ and ∆
.
We consider ∆
to be Gehring compatible w.r.t ∆,
if the maximal angle between e
2
or e
3
and N
∆
(the
normal vector to ∆), is greater then a predefined mea-
sure suited to the desired predefined maximal allowed
distortion, i.e. max {(e
2
,N
∆
), (e
3
,N
∆
)}≥α.
We project ∆
orthogonally onto the plane included
in ∆ and insert it to the patch of ∆, iff it is Gehring
compatible w.r.t ∆.
e
e
e
1
2
3
N
∆
∆
∆
'
Figure 3: Gehring Compatible Triangles. Here a general
projection direction N
∆
is depicted.
We keep adding triangles to the patch of ∆ moving
from an added triangle to its neighbors (of course)
while avoiding repetitions, till no triangles can be
added.
If by this time all triangles where added to the patch
we have concluded. Otherwise, chose a new triangle
that has not been projected yet, to be the starting trian-
gle of a new patch. A pseudocode for this procedure
can be easily written.
We conclude this section with the following re-
marks: One should keep in mind that the above given
algorithm, as for any other flattening method, is lo-
cal. Indeed, in a sense the (proposed) algorithm gives
a measure of “globality” of this intrinsically local
VISAPP 2006 - IMAGE ANALYSIS
424
process. Our algorithm is best suited for highly folded
surfaces, because of its intrinsic locality on the one
hand and computational simplicity, on the other.
4 EXPERIMENTAL RESULT
We present some experimental results obtained by ap-
plying the algorithm presented in the previous sec-
tion. In each of the examples both the input sur-
face and a flattened representation of some patch are
shown. Distortion error is computable according to
the bounds given by Theorem 1. Details on the res-
olution of the mesh and also the number of patches
may also be given.
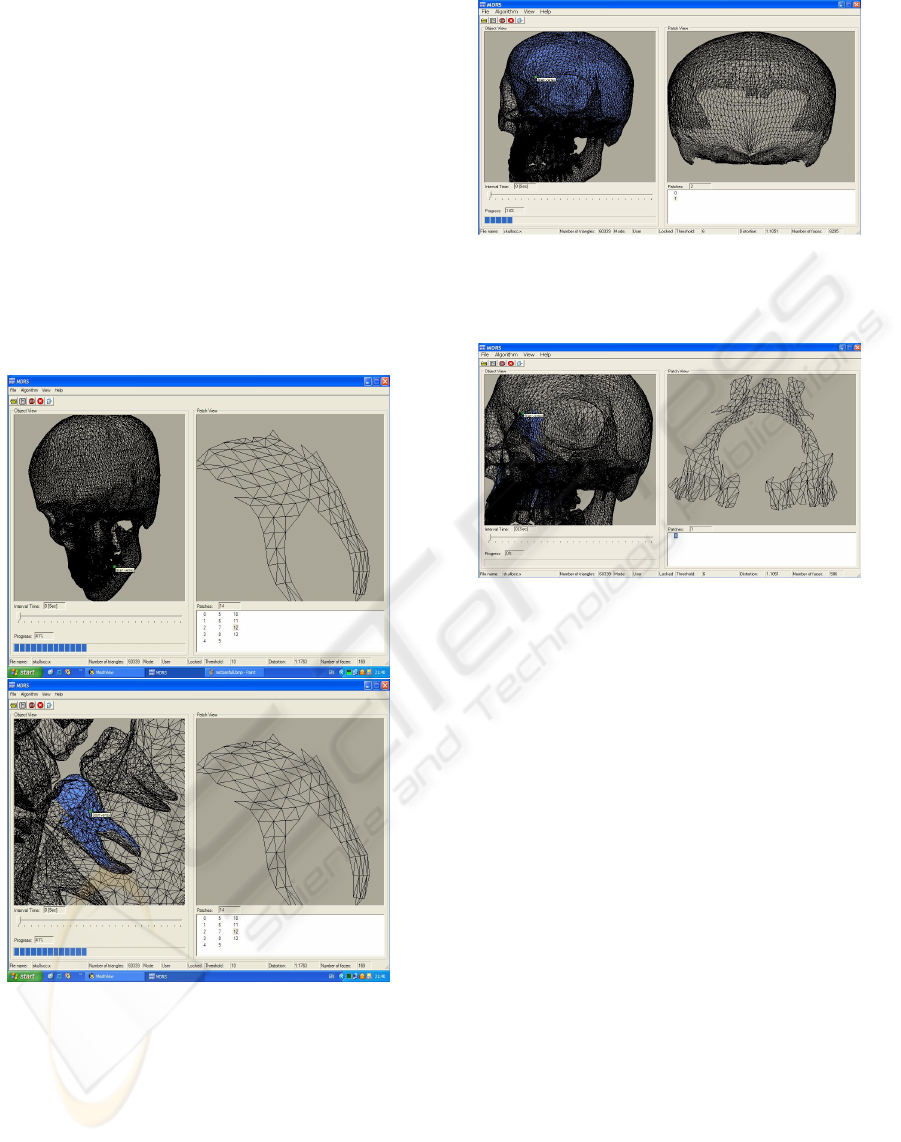
Figure 4: Tooth model: (a) and (b) have resolution of 60,339
triangles yet the resolution of the visualization is different.
No change was caused to the flattening of the teeth. In both
cases the dilatation is 1.1763.
5 CONCLUDING REMARKS
Our new quasi-conformal-based algorithm for flat-
tened representation of polyhedral meshes has been
Figure 5: Skull model: resolution of 60,339 triangles. Ini-
tial triangle in the frontal region. Here α =6
0
and the
dilatation is 1.1051.
Figure 6: Skull model: resolution of 60,339 triangles. Ini-
tial triangle in the sinuses region. Here α =6
0
and the
dilatation is 1.1051.
successfully applied to colon imaging, with minimal
dilatation introduced by the flattening. The algorithm
is based upon the works of Gehring-V¨aisala and oth-
ers concerning the existence of quasi-isometric/quasi-
conformal mappings between Riemannian manifolds.
From the implementation results it is evident that
this algorithm, while being simple to program as well
as efficient, yields good flattening results and main-
tains small dilatations even in areas where curvature is
large and good flattening is a challenging task. More-
over, since there is a simple way to assess the result-
ing dilatation, the algorithm is implementable in such
a way that the user can set in advance an upper bound
on the resulting dilatation.
An additional advantage of the presented algorithm
resides in the fact that in contrast to some of the re-
lated works, no use of derivatives is made. Conse-
quently the algorithm is applicable to noisy data as
well.
The main issue which calls for further study is re-
lated to the inherent locality of the quasi-conformal
and quasi-isometric geometric mapping adopted in
our approach. It is important to incorporate properties
in a well-defined and precise manner. Such a general-
ized approach, which is currently under investigation,
MINIMAL DISTORTION MAPPINGS OF SURFACES FOR MEDICAL IMAGES
425

Figure 7: Colon CT-Images: Triangulated colon surface
taken from 3 slices of human colon scan. Images are in
curtesy of Dr. Doron Fisher from Rambam Madical Center
in Haifa.
will permit “gluing” two neighbouring patches while
keeping fixed bounded dilatation.
ACKNOWLEDGMENTS
The authors would like to thank Ofir Zeitoun and
Efrat Barak and Amiad Segal for their dedicated and
skillful programming of the algorithms. Emil Saucan
is supported by the Viterbi Postdoctoral Fellowship.
Research supported in part by the Ollendorf Center.
REFERENCES
Caraman, P. (1974) n-Dimensional Quasiconformal (QCf)
Mappings. Editura Academiei Rom
ˆ
ane, Bucharest,
Abacus Press, Tunbridge Wells Haessner Publishing,
Inc., Newfoundland, New Jersey.
Gehring, W. F. and V
¨
aisala, J. (1965). The coefficients of
quasiconformality. In Acta Math. 114, pp. 1-70.
Gu, X. and Yau, S. T. (2002). Computing Conformal Struc-
ture of Surfaces. In Communications In Information
and Systems, Vol. 2, No. 2, pp. 121-146.
Gu, X. and Yau, S. T. (2003). Global Conformal Surface Pa-
rameterization In Eurographics Symposium on Geom-
etry Processing.
Haker, S. Angenet, S. Tannenbaum, A. Kikinis, R. (2000)
Non Distorting Flattening Maps and the 3-D visual-
ization of Colon CT Images. IEEE Transauctions on
Medical Imaging, Vol. 19, NO. 7.
Haker, S. Angenet, S. Tannenbaum, A. Kikinis, R. Sapiro,
G. Halle, M. (2000) Conformal Surface Parametriza-
tion for Texture Mapping. IEEE Transauctions on Vi-
sualization and Computer Graphics, Vol. 6, NO. 2.
Hara, A., Johnson, C., Reed, J., Ehman, R., Ilstrup, D.
(1996) Colorectal polyp detection with CT cologra-
(a)
(b)
Figure 8: Colon Flattening: One half of the colon taken
from 3 slices. (a) before flattening and (b) after.
phy: two- versus three-dimensional techniques. Radi-
ology, vol. 200, pp. 49-54.
Hurdal, M. K., Bowers, P. L., Stephenson, K., Sumn-
ers, D. W. L., Rehm, K., Schaper. K., Rottenberg,
D. A. (1999) Quasi Conformally Flat Mapping the
Human Crebellum, In Medical Image Computing
and Computer-Assisted Intervention -MICCAI’99, (C.
Taylor and A. Colchester. eds), vol. 1679, pp. 279-289.
Springer-Verlag, Berlin.
Paik, D., Beaulieu, C., Jeffrey, R., Karadi C., and Napel, S.
(1999) Visualizations modes for CT colonography us-
ing cylindrical and planar projections. Technical Re-
port, Department of Radiology, Stanford University
School of Medicine, Stanford, CA.
Pey
´
e, G. and Cohan, L. (2005) Geodesic Computations for
Fast and Accurate Surface Flattening. preprint.
Sheffer, A. de Stuler, E. (2001) Parametrization of Faceted
Surfaces for Meshing Using Angle Based Flattening.
In Enginneering with Computers, vol. 17, pp. 326-
337.
Sorkine, O., Cohen-Or, Daniel, Goldenthal, R. and Lischin-
ski, D. (2005) Bounded-distorsion Piecewise Mesh
Parametrization. preprint.
V
¨
aisal
¨
a, J. (1971). Lectures on n-dimensional quasicon-
formal mappings. Lecture Notes in Mathematics 229,
Springer-Verlag, Berlin - Heidelberg - New-York.
VISAPP 2006 - IMAGE ANALYSIS
426
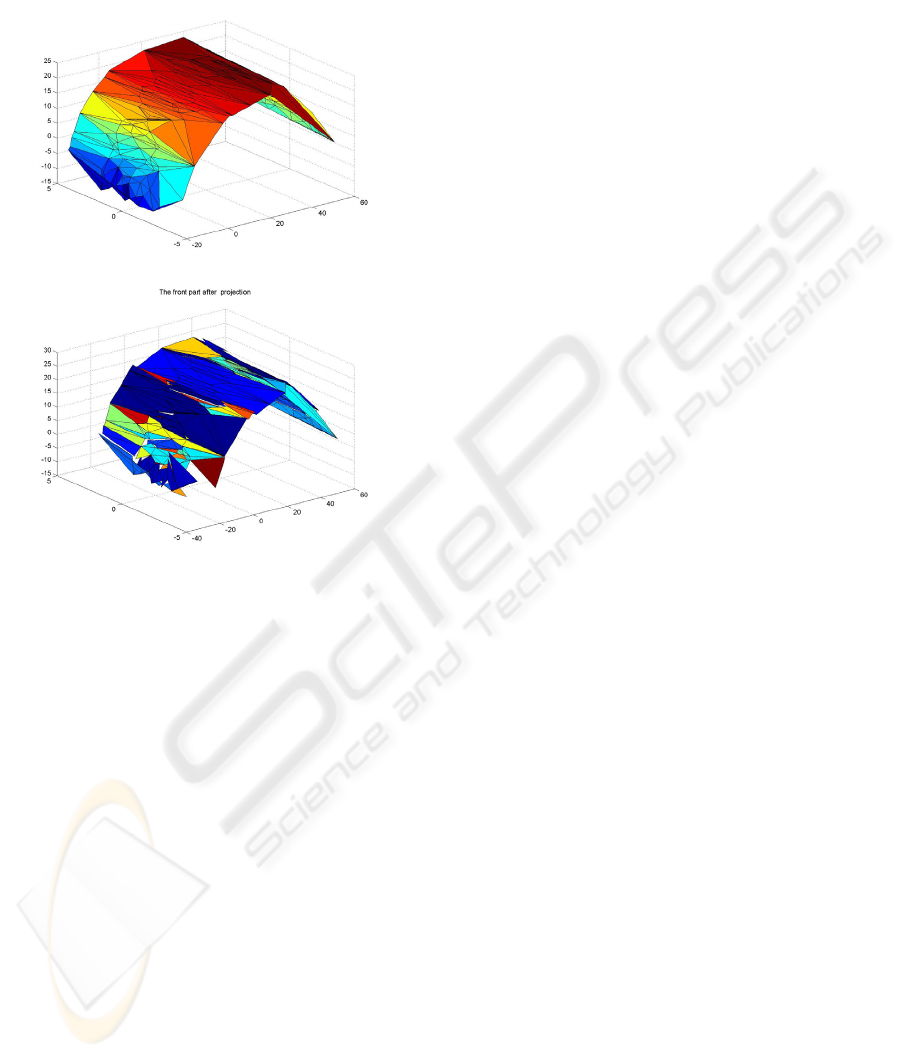
(a)
(b)
Figure 9: Colon Flattening: Second half of the colon slices.
(a) before flattening and (b) flattened.
MINIMAL DISTORTION MAPPINGS OF SURFACES FOR MEDICAL IMAGES
427
