EVALUATING THE POTENTIAL OF CLUSTERING

TECHNIQUES FOR 3D OBJECT EXTRACTION FROM LIDAR

DATA

Farhad Samadzadegan, Mehdi Maboodi, Sara Saeedi, Ahmad Javaheri

Department of Geomatics Engineeering, University of Tehran, Tehran, Iran

Keywords: Clustering, LIDAR, K-Mean, FCM, SOM, Filtering, 3D Objects.

Abstract: During the last decade airborne laser scanning (LIDAR) has become a mature technology which is now

widely accepted for 3D data collection. Nevertheless, these systems have the disadvantage of not

representing the desirable bare terrain, but the visible surface including vegetation and buildings. To

generate high quality bare terrain using LIDAR data, the most important and difficult step is filtering, where

non-terrain 3D objects such as buildings and trees are eliminated while keeping terrain points for quality

digital terrain modelling. The main goal of this paper is to investigate and compare the potential of

procedures for clustering of LIDAR data for 3D object extraction. The study aims at a comparison of K-

Means clustering, SOM and Fuzzy C-Means clustering applied on range laser images. For evaluating the

potential of each technique, the confusion matrix concept is employed and the accuracy evaluation is done

qualitatively and quantitatively.

1 INTRODUCTION

In recent years LIDAR data has become as a highly

acknowledged data source for interactive mapping

of 3D man-made and natural objects from the

physical earth’s surface. The dense and accurate

recording of surface points has encouraged research

in processing and analysing the data to develop

automated processes for feature extraction, object

recognition and object reconstruction. However, the

algorithm for segmentation of this kind of data, i.e.

distinguish between ground surface and objects on

the surface, is still on going researched (Haala and

Brenner 1999; Axelsson, 1999; Maas and

Vosselman, 2001).

Nowadays, laser-scanning systems are able to

collect of two different types from the ground

surface and the objects over it; first-pulse and last-

pulse data. Laser pulses have one important

advantage that partially they penetrate the vegetation

in gaps between leaves and obtain data reflected

from points underneath the vegetation. This property

of the laser defines the difference between first- and

last- pulse data. That means in first-pulse data, the

data of the vegetation’s surface is available, while it

is not the case in last-pulse. The other main property

of laser scanning systems is the ability to provide the

range data from the objects in addition to the

reflectance image data (intensity data). This range

data obtained from the elevation points over the

earth’s surface or other 3D objects can be converted

to a digital range image. Therefore the laser

scanners, nowadays, can provide both range image

and intensity image in two different types, first- and

last-pulse data (Sithole, 2003; Roggero, 2002).

The paper shows the potential of the analysis of

height texture for the automatic segmentation of

LIDAR regular range datasets and 3D objects

extraction in the segmented data. Based on the

definition and computation of a number of texture

measures used as bands in three clustering

approaches (i.e. K-Mean, FCM and SOM), 3D

objects like buildings and trees can be recognized

from bare terrain.

2 CLUSTERING OF LIDAR DATA

Cluster analysis is a difficult problem because many

factors (such as effective similarity measures,

criterion functions, algorithms and initial conditions)

come into play in devising a well tuned clustering

149

Samadzadegan F., Maboodi M., Saeedi S. and Javaheri A. (2006).

EVALUATING THE POTENTIAL OF CLUSTERING TECHNIQUES FOR 3D OBJECT EXTRACTION FROM LIDAR DATA.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 149-154

DOI: 10.5220/0001378301490154

 SciTePress

technique for a given clustering problem. Cluster

analysis is an unsupervised learning method that

constitutes a cornerstone of an intelligent data

analysis process. It is used for the exploration of

inter-relationships among a collection of patterns, by

organizing them into homogeneous clusters. It is

called unsupervised learning because unlike

classification (known as supervised learning), no a

priori labeling of some patterns is available to use in

categorizing others and inferring the cluster structure

of the whole data. Intra-connectivity is a measure of

the density of connections between the instances of a

single cluster. A high intra-connectivity indicates a

good clustering arrangement because the instances

grouped within the same cluster are highly

dependent on each other. Inter-connectivity is a

measure of the connectivity between distinct

clusters. A low degree of interconnectivity is

desirable because it indicates that individual clusters

are largely independent of each other.

K-Means: The most well-known partitioning

algorithm is the K-Means (

Rottensteiner and Briese,

2002

). The K-Means method partitions the data set

into k subsets such that all points in a given subset

are closest to the same centre. In detail, it randomly

selects k of the instances to represent the clusters.

Based on the selected attributes, all remaining

instances are assigned to their closer centre. K-

Means then computes the new centres by taking the

mean of all data points belonging to the same

cluster. The operation is iterated until there is no

change in the gravity centres. If k cannot be known

ahead of time, various values of k can be evaluated

until the most suitable one is found. The

effectiveness of this method as well as of others

relies heavily on the objective function used in

measuring the distance between instances. The

difficulty is in finding a distance measure that works

well with all types of data.

FCM: Traditional K-Means clustering

approaches generate partitions; in a partition, each

pattern belongs to one and only one cluster. Hence,

the clusters in a hard clustering are disjoint. Fuzzy

clustering extends this notion to associate each

pattern with every cluster using a membership

function. Larger membership values indicate higher

confidence in the assignment of the pattern to the

cluster. One widely used algorithm is the Fuzzy C-

Means (FCM) algorithm, which is based on K-

Means. FCM attempts to find the most characteristic

point in each cluster, which can be considered as the

“centre” of the cluster and, then, the grade of

membership for each instance in the clusters.

Let us assume as a Fuzzy C-Means Functional

where,

[

]

{

}

cjyY

,1∈= is the set of centers of

clusters;

)(

xE is a dissimilarity measure (distance

or cost) between the sample

x and the center

of a specific cluster j; U = [u

] is the c × n fuzzy c-

partition matrix, containing the membership values

of all samples in all clusters;

),1[ ∞∈m

is a control

parameter of fuzziness.

∑∑

jkm

xEuYUJ

)()(),(

(1)

The clustering problem can be defined as the

minimization of J

with respect to Y, under the

probabilistic constraint:

∑

(2)

The Fuzzy C-Means algorithm consists in the

iteration of the following formulas:

()

∑

for all j, (3)

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≠∀=

∀〉

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

∑

jluandxEif

kjxEif

lkkj

0)(1

,0)(

)(

Where, in the case of the Euclidean space:

)(

jkkj

yxxE −= (4)

SOM: Among the other types of artificial neural

networks, the self organizing neural network

resembles real biological neural networks more than

the other types. It was first introduced by Kohonen

(Kohonen, 1989) as the "Self Organizing Feature

Map". SOM can be seen as an extension to the

competitive learning neural network. In the SOM,

the output units are ordered in some fashion, often in

a two dimensional grid or array. The ordering of

output units determines which neurons are

neighbours.

When learning patterns are presented to the

SOM, the weights to the output neurons are thus

adapted such that the order present in the input space

is preserved in the output space. This means that

learning patterns which are near to each other in the

input space must be mapped on output units which

are also near to each other.

SOM can be described step by step as follows:

VISAPP 2006 - IMAGE UNDERSTANDING

150

1. Random Initialization of neurons weights (W

where i and j are the identifiers of the input and

output neurons, respectively.

2. Introduce randomly selected learning pattern (Pj)

to the network. Compute the dissimilarity

between input pattern and all neurons in the

output layer of SOM and determine the winner

(closest) neuron, using the Euclidean distance,

where

is the input to neuron i at iteration n.

()

∑

−=

wPd

S = max (d

) (6)

3. Find winner neuron neighbours using defined

neighbourhood function.

4. Update the weights of winner and its neighbours,

using Hebbian learning rule.

(

)

iji

wPNww −⋅⋅+=

′

(7)

using Eq. (7)

denotes the learning rate in the

iteration n expressed as below and

(

)

′

is the

neighbourhood function of the winner neuron i'.

1001

≤≤

5. Repeat step 1 to 4, until network converges.

6. Introduce all patterns to the network.

7. Find winner neuron for each input pattern.

8. Assign presented pattern to the cluster which

winner neuron points to it.

2.1 Clustering Validity Checking

Clustering is perceived as an unsupervised process

since there are no predefined classes and no

examples that would show what kind of desirable

relations should be valid among the data. As a

consequence, the final partitions of a data set require

some sort of evaluation in most applications

(Kohonen, 1989). For instance questions like “how

many clusters are there in the data set?”, “does the

resulting clustering scheme fits our data set?”, “is

there a better partitioning for our data set?” call for

clustering results validation and are the subjects of a

number of methods discussed in the literature. They

aim at the quantitative evaluation of the results of

the clustering algorithms and are known under the

general term cluster validity methods.

The procedure of evaluating the results of a

clustering algorithm is known under the term cluster

validity. In general terms, there are three approaches

to investigate cluster validity. The first is based on

external criteria. This implies that we evaluate the

results of a clustering algorithm based on a pre-

specified structure, which is imposed on a data set

and reflects our intuition about the clustering

structure of the data set. The second approach is

based on internal criteria. We may evaluate the

results of a clustering algorithm in terms of

quantities that involve the vectors of the data set

themselves (e.g. proximity matrix). The third

approach of clustering validity which we used in our

research work is based on relative criteria.

Here the basic idea is the evaluation of a

clustering structure by comparing it to other

clustering schemes, resulting by the same algorithm

but with different parameter values. There are two

criteria proposed for clustering evaluation and

selection of an optimal clustering scheme:

1- Compactness, the members of each cluster should

be as close to each other as possible. A common

measure of compactness is the variance, which

should be minimized.

2- Separation, the clusters themselves should be

widely spaced. There are three common

approaches measuring the distance between two

different clusters:

Single linkage: It measures the distance between

the closest members of the clusters.

Complete linkage: It measures the distance

between the most distant members.

Comparison of centroids: It measures the

distance between the centers of the clusters.

The two first approaches are based on statistical

tests and their major drawback is their high

computational cost. Moreover, the indices related

to these approaches aim at measuring the degree

to which a data set confirms a-priori specified

scheme. On the other hand, the third approach

aims at finding the best clustering scheme that a

clustering algorithm can be defined under certain

assumptions and parameters.

A number of validity indices have been defined

and proposed in literature for each of above

approaches (Halkidi et al., 2001). The indices which

are used in this paper are the Davies-Bouldin (DB)

index and Hubert index.

Davies-Bouldin index: A similarity measure R

between the clusters C

and C

is defined based on a

measure of dispersion of a cluster C

and a

dissimilarity measure between two clusters d

(Davies and Bouldin, 1979). One choice for R

that

satisfies the above conditions is:

= (s

)/d

i j

(9)

Then the DB index is defined as:

(

)

(

)

EVALUATING THE POTENTIAL OF CLUSTERING TECHNIQUES FOR 3D OBJECT EXTRACTION FROM LIDAR

DATA

151

∑

inc

(10)

}max{

iji

RR = i=1, …, n

i≠j

It is clear for the above definition that DB

is the

average similarity between each cluster and its most

similar one. It is desirable for the clusters to have the

minimum possible similarity to each other; therefore

we seek clustering that minimizes DB. The DB

index exhibits no trends with respect to the number

of clusters and thus we seek the minimum value of

in its plot versus the number of clusters.

Hubert Index: The definition of the Hubert Γ

index (Hubert, 1985) is given by the Eq. (11) where

N is the number of objects in a dataset, M=N(N-1)/2,

P is the proximity matrix of the data set and Q is an

N×N matrix whose (i,j) element is equal to the

distance between the representative points (v

, v

) of

the clusters where the objects x

and x

belong.

()()

∑∑

−

=+=

=Γ

jiQjiP

3 EXPERIMENTS AND RESULTS

The airborne LIDAR data used in the experimental

investigations have been recorded with TopScan

Airborne Laser Terrain (TopScan, 2004). The

average density of the measured 3D points is about

1.7 per m

. Figure 1 shows the first-pulse and the

last-pulse LIDAR range image from the city of

Rheine in Germany. The impact of the Vegetation in

the first- and last- pulse images can be easily

recognized by comparing the two images of this

figure.

First pulse range Last pulse range

Figure 1: LIDAR dataset.

The first step in every clustering process is to

extract the feature image bands. The features of

theses feature bands should carry useful textural or

surface related information to differentiate between

regions related to the surface.

Relief range first Top-Hat range last

NDVI range

Figure 2: Three applied Feature.

Several features have been proposed for

clustering of range data. Axelsson (1999) employs

the second derivatives to find textural variations and

Maas (1999) utilizes a feature vector including the

original height data, the Laplace operator, maximum

slope measures and others in order to classify the

data. In our work, three types of features are taken

into account. These features are: NDDI ratio,

Morphological Opening and relief of range

information of LIDAR data. Figure 2 shows the

output of three mentioned features on LIDAR data

set.

To assess the validity of clustering algorithm we

experimented the algorithm for n

= 1 to n

= 10.

Using Davies-Bouldin (DB) and Hubert indices,

three clusters are optimum according to input data.

Plot of the indices

versus n

is depicted in Figure 3.

Hubert Index DB Index

Figure 3: Optimum Clusters.

Figure 4 shows outputs of the K-Mean, FCM and

SOM algorithms for the situation of optimum cluster

number (i.e. 3).

Maximum Hubert Index

Optimum Cluster

Minimum DB Index

Optimum Cluster

(

)

VISAPP 2006 - IMAGE UNDERSTANDING

152

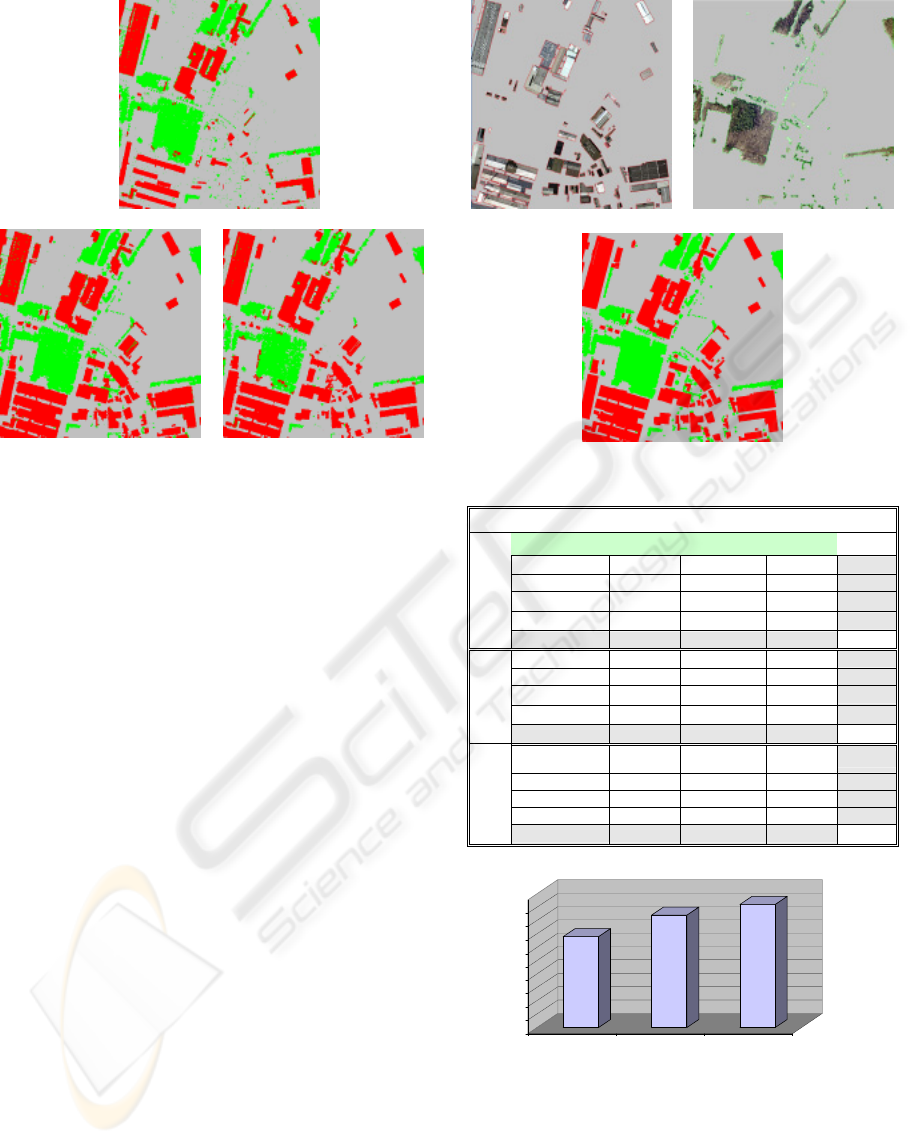
K-Means

SOM FCM

Figure 4: The situation of optimum cluster number.

4 ANALYSIS OF CLUSTERING

RESULTS

After performing clustering algorithms (K-Means,

FCM and SOM), it is necessary to assess their

accuracies. In this context, the term accuracy means

the level of agreement between labels assigned by

the clustering algorithm and class allocation based

on truth data. To generate an appropriate truth data,

we used aerial image of the scene and first-pulse

range of LIDAR data. Using these data we produced

the ortho-image. Then, Buildings and vegetation

have been digitized, manually. Figure 5 shows the

truth data.

The method used in this paper to assess the

accuracy of clustering results is based on analysis of

the confusion matrix. The most common tool for the

clustering accuracy assessment is in term of a

confusion matrix. The columns in a confusion

matrix represent truth data, while rows represent the

labels assigned by the clustering algorithm. The

confusion matrix of K-Means, FCM and SOM

results, are presented in Table 1, respectively.

Several indices of clustering accuracy can be

derived from the confusion matrix. One of these

indices is "overall accuracy", which is obtained by

dividing the sum of main diagonal entries of the

confusion matrix by the total number of patterns.

Figure 6 shows the "overall accuracy" of K-Means,

FCM and SOM.

Man-made objects Vegetation

Truth Data

Figure 5: The truth data.

Table 1: Confusion matrix of K-Means, FCM and SOM.

Truth Data

Buildings Vegetation Bare-Land Sum

Buildings 64338 1551 338 66227

Vegetation 3561 58692 5930 68183

Bare-Land 54341 10509 290740 355590

K-Means

Sum 122240 70752 297008 490000

Buildings Vegetation Bare-Land Sum

Buildings 108835 4292 1697 114824

Vegetation 921 49488 517 50926

Bare-Land 12484 16972 294794 324250

FCM

Sum 122240 70752 297008 490000

Buildings Vegetation Bare-Land Sum

Buildings 116002 591 4666 121259

Vegetation 2224 63953 3344 69521

Bare-Land 4014 6208 288998 299220

SOM

Sum 122240 70752 297008 490000

The accuracy measurements shown above,

namely, the overall accuracy and producer's

accuracy, though quite simple to use, are based on

either the principal diagonal or columns of confusion

matrix only, which does not use the information

from the whole confusion matrix. A multivariate

Figure 6: Overall accuracy of K-Means, FCM and SOM.

84%

92%

96%

50%

55%

60%

65%

70%

75%

80%

85%

90%

95%

100%

K-Means FCM SOM

84%

92%

96%

EVALUATING THE POTENTIAL OF CLUSTERING TECHNIQUES FOR 3D OBJECT EXTRACTION FROM LIDAR

DATA

153

index called the kappa coefficient (Cohen, 1960) has

found favour. The kappa coefficient is defined as

Eq. (12) where k is number of clusters,

and

are the marginal totals of row i and column i,

respectively and N is the total number of patterns.

()

∑

∑∑

⋅−

⋅−⋅

iiii

MMN

MMMN

(12)

Figure 7 shows the "kappa coefficient" of K-

Means, FCM and SOM.

The value of kappa for each cluster can be

derived as follows:

iii

iiii

MMMN

+++

⋅−⋅

⋅

−

⋅

(13)

5 CONCLUSION

Airborne laserscanning is being used for an

increasing number of mapping and GIS data

acquisition tasks. Besides the original purpose of

digital terrain model generation, new applications

arise in the automatic detection and modeling of

objects such as buildings or vegetation for the

generation of 3-D city models. A crucial prerequisite

for the automatic extraction of objects on the Earth's

surface from LIDAR height data is the clustering of

datasets. Besides the height itself, height texture

defined by local variations of the height is a

significant feature of objects to be recognized.

We have presented the results of applying three

different clustering techniques on LIDAR data for

3D object extraction. Using these methods we have

been able to filter non-terrain 3D objects such as

buildings and trees while keeping terrain points for

quality digital terrain modelling.

However, as it appear from obtained results of

applying different clustering methods on LIDAR

data; the SOM has the most reliable potential for

extraction of 3D objects like building and trees from

bare terrain.

REFERENCES

Axelsson, P., 1999. Processing of laser scanner data –

algorithms and applications. ISPRS Journal of

Photogrammetry and Remote Sensing, 54(2-3): 138-

147.

Cohen, J. 1960, "A coefficient of agreement for nominal

scales", "Educational and Psychological

Measurement", Vol. 20(1): pp. 37-46

Davies, D.L. and Bouldin, D.W. (1979). "A Cluster

Separation Measure." IEEE Transactions on Pattern

Analysis and Machine Intelligence, 1(2), 224–227.

Haala,N and Brenner, "Extraction of buildings and trees

in urban environments", ISPRS Journal of

Photogrammetry & Remote Sensing V 54(2-3), 130-

137 (1999).

Halkidi, M., Batistakis, I.and Vazirgiannis, M. (2001).

"On Clustering Validation Techniques", Journal of

Intelligent Information Systems, 17:2/3, 107–145

Hubert, L.J. Arabie, P., 1985, "Comparing

partitions",

Journal of Classification, Vol. 2, pp. 193-218.

Kohonen, T., 1989, "Self-Organization and Associative

Memory", Springer-Verlag.

Maas, H.G., 1999. The potential of height texture

measures for the segmentation of airborne

laserscanner data.

Mass, H. Vosselman, G. (2001), "Two algorithms for

extracting building models from raw laser" OEEPE

Workshop on Airborne Laserscanning and

Interferometric SAR for Detailed Digital Elevation

Models, Stockholm, Official Publication OEEPE

no.40,2001, 62-72

Roggero, M., 2002. "Object segmentation with region

growing and principal component analysis",

International Archives of Photogrammetry and

Remote Sensing, Vol. 34, Part 3A, Graz, Austria

Rottensteiner, F., Briese, Ch., 2002. "A new method for

building extraction in urban areas from high-resolution

LIDAR data", International Archives of

Photogrammetry and Remote Sensing, Vol. 34, Part

3A, Graz, Austria

Sithole, George, Vosselman, George,2003, "Comparison

of Filtering Algorithm"Proceedings of the Fourth

International Airborne Remote Sensing Conference,

Ottawa, Canada. pp. 154-161.

TopScan, 2004. Airborne LIDAR Mapping Systems.

http://www.topscan.de/en/luft/messsyst.html (accessed

10 Feb. 2004)

69%

86%

92%

50%

55%

60%

65%

70%

75%

80%

85%

90%

95%

100%

K-Means FCM SOM

69%

86%

92%

ure 7: Ka

a coefficient of

-Means

FCM and SOM.

VISAPP 2006 - IMAGE UNDERSTANDING

154