PACKET SCHEDULING AND PRICING BASED ON INFLICTED

DELAY

Ari Viinikainen

Department of Mathematical Information Technology, University of Jyväskylä

P.O. Box 35 (Agora)

40014 University of Jyväskylä, Finland

Keywords:

Pricing, revenue optimization, delay, Quality of Service (QoS).

Abstract:

An adaptive packet scheduling method is presented in this paper. The adaptive weights of a scheduler are

chosen based on maximizing the revenue of the network service provider. The pricing scenario is based on

the delay that a connection will inﬂict to other connections. The features of the adaptive weight updating

algorithm are simulated, analyzed and compared to a constant weight algorithm.

1 INTRODUCTION

Internet services should be focused more on service

alignment and revenue generation. This requires new

ideas for network management solutions. To meet

growing organizational demands, policy-based man-

agement is one solution that will allow organiza-

tions to prioritize networking resources such as band-

width, application access and security clearance based

on individual users. These policy-based manage-

ment methods will have to be self-deploying, self-

conﬁguring and self-healing, automatically discov-

ering any changes taking place in the network in-

frastructure and dynamically building and altering

policies for accessing resources based on needs. By

combining scheduling and revenue issues together an

efﬁcient method can be built to allocate network re-

sources in optimal and proﬁtable way.

The packet scheduling algorithms can be classi-

ﬁed into two categories, depending on the need for

sorting the packets in the scheduler. Those that are

based on packet sorting, need to maintain a “virtual

time”, that is used to calculate the order of the pack-

ets. These kinds of schedulers provide good fair-

ness and low latency but due to the complexity in

computation of the parameters used for sorting, they

lack efﬁciency. Weighted Fair Queueing (WFQ) (De-

mers et al., 1989; Parekh and Gallager, 1993) was

a ﬁrst proposal of these kinds. Later other propos-

als as Self-clocked Fair Queueing (SCFQ) (Golestani,

1994), Worst-case Fair Weighted Queueing (WF

(Bennett and Zhang, 1996), Start-time Fair Queue-

ing (SFQ) (Goyal et al., 1997) and Frame-Based Fair

Queueing (FFQ) (Stiliadis and Varma, 1998) have

been proposed to combat the lack of efﬁciency.

Schedulers that handle packets in a round robin

manner, like Deﬁcit Round Robin (DRR) (Shreed-

har and Varghese, 1996), are in the other category.

These have low complexity but they are not as good

in fairness and latency. Several algorithms have been

proposed for improving the latency and fairness in a

round robin based schemes, such as Advanced Round

Robin (ARR) (Marosits et al., 2001), Smoothed

Round Robin (SRR) (Guo, 2001), Pre-order deﬁcit

round robin (Tsao and Lin, 2001), Nested DRR (Kan-

here and Sethu, 2001), Elastic Round Robin (ERR)

(Kanhere et al., 2002), Stratiﬁed Round Robin (Ram-

abhadran and Pasquale, 2003) and Fair Round Robin

(FRR) (Yuan and Duan, 2005).

This paper proposes a scheduling model that guar-

antees that the latencies for different service classes

are appropriate and at the same time optimizes the

network service provider’s revenue. This work con-

tinues the work in (Viinikainen et al., 2004) and (Jout-

sensalo et al., 2005) where the pricing of a connec-

tion was based on delay and bandwidth that the con-

nection itself obtains, respectively. The proposed al-

gorithm that is presented in this paper ensures less

delay for the users paying more for the connection

(i.e. higher service class) than those paying less. The

proposed method also penalizes by pricing those cus-

tomers, who induce the most delay in the network.

Thus, this approach yields a tempting scenario for

customers and the service provider. The closed form

113

Viinikainen A. (2006).

PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY.

In Proceedings of the International Conference on e-Business, pages 113-117

DOI: 10.5220/0001424201130117

 SciTePress

formula for updating weights is independent on any

statistical behavior of the connections. Therefore, it is

also robust against erroneous estimates of customers’

behavior.

The rest of the paper is organized as follows. First,

in Section 2 the scheduler is discussed and the pro-

posed pricing scenario is deﬁned, whilst experiments

justifying the analytical derivation are made in Sec-

tion 3. Section 4 contains discussion of theory and

experiments and Section 5 concludes the study.

2 THE PACKET SCHEDULER

AND DELAY

Let us consider a packet scheduler which receives

packets to be delivered from m different queues (i.e.

classes). Now, let T be the processing time of the

classiﬁer for transmitting a data packet from one

queue to the output of a packet scheduler. For any

connection k there are N

(t) packets in the queue of

class i at some time t. Total number of packets in the

queue i at the time t is therefore

(t) =

(t)

k=1

(t), (1)

where K

(t) is the total number of connections in the

class i at time t.

Now, every packet in the queue increases delay for

the other connections in the queue so a new connec-

tion k appearing at time t in class i will increase the

delay to the other connections by a value proportional

to N

(t)

(t) =

(t)T

(t)

, (2)

where T can be scaled to T = 1 without loss of gener-

ality and w

(t) = w

, i = 1, . . . , m are weights allo-

cated for each class as a new connection in any class

will inﬂict delay on the other classes depending on

amount of processing time of the scheduler allotted to

each class. The overall delay in class i is then

(t) =

k=1

, (3)

where the time index t has been dropped for conve-

nience until otherwise stated. The natural constraints

for the weights are

> 0 (4)

and

i=1

= 1. (5)

For every connection the pricing is based on the rela-

tive increase in delay that it produces. Every connec-

tion induce delay and those connections that induce

more delay than the connections on average will pay

more for the connection.

Deﬁnition 1. For each service class the function

k=1

+ s

, r

> 0, s

> 0, p > 0 (6)

is called a polynomial pricing function.

In the polynomial pricing function r

is a base price

of a connection in the class i, s

is a penalty factor

that increases the price for those connections which

induce more delay and p assures that the price does

not grow too rapidly with the delay. The total revenue

of the operator is

R =

i=1

k=1

i=1

k=1

+ s

(7)

Theorem 1. Optimal weights for the revenue R under

the polynomial pricing model is

p−1

j=1

p−1

. (8)

when 0 < p < 1.

Proof. By using Lagrangian approach, the revenue

can be presented in the form

R =

i=1

k=1

+ s

+ λ(1 −

i=1

). (9)

Optimal weights are obtained from the ﬁrst deriva-

tive

∂R

∂w

k=1

−ps

p−1

− λ = 0. (10)

Because Lagrangian solution

∂F

∂λ

= 0 (11)

yields

j=1

= 1, then



−ps



p−1

(−ps

)

p−1

j=1

(−ps

)

p−1

j=1

(−ps

)

p−1

j=1

p−1

. (12)

ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS

114

From the expression (12) it is seen that λ has the form

p−1

j=1

p−1

, (13)

λ =

j=1

. (14)

Thus the ﬁrst order derivative is

∂R

∂w

k=1

−ps

p−1

−

j=1

, (15)

and so the second order derivative is

∂

∂w

k=1

−(p − 1)

−ps

p−2

< 0 (16)

when 0 < p < 1. In that condition, R is concave with

respect to the weights w

, and the optimal solution is

unique.

By using optimal weights (8), revenue R can be

expressed as follows:

R =

i=1

k=1

i=1

p−1

j=1

p−1

i=1

+ s

p−2

p−1

−1

p−1

j=1

p−1

. (17)

3 EXPERIMENTS

In this section the operation of the pricing algorithm

(6) with p =

and m = 3 service classes is demon-

strated by simulation. The optimal weights (12) are

compared with a constant weight (w

= 1/2, w

1/3 and w

= 1/6) version of the algorithm.

The processing time of the server is chosen as

T = 1/1000 s/packet. The life time of a connec-

tion is exponentially distributed. The arrival rates of

the connections are Poisson distributed and they are

= 0.30, α

= 0.40 and α

= 0.50 per unit

time for the gold, silver, and bronze classes, respec-

tively. The duration parameters (i.e. "decay rates")

for the connections are β

= 0.015, β

= 0.013 and

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Time[s]

Number of connections

Bronze

Silver

Gold

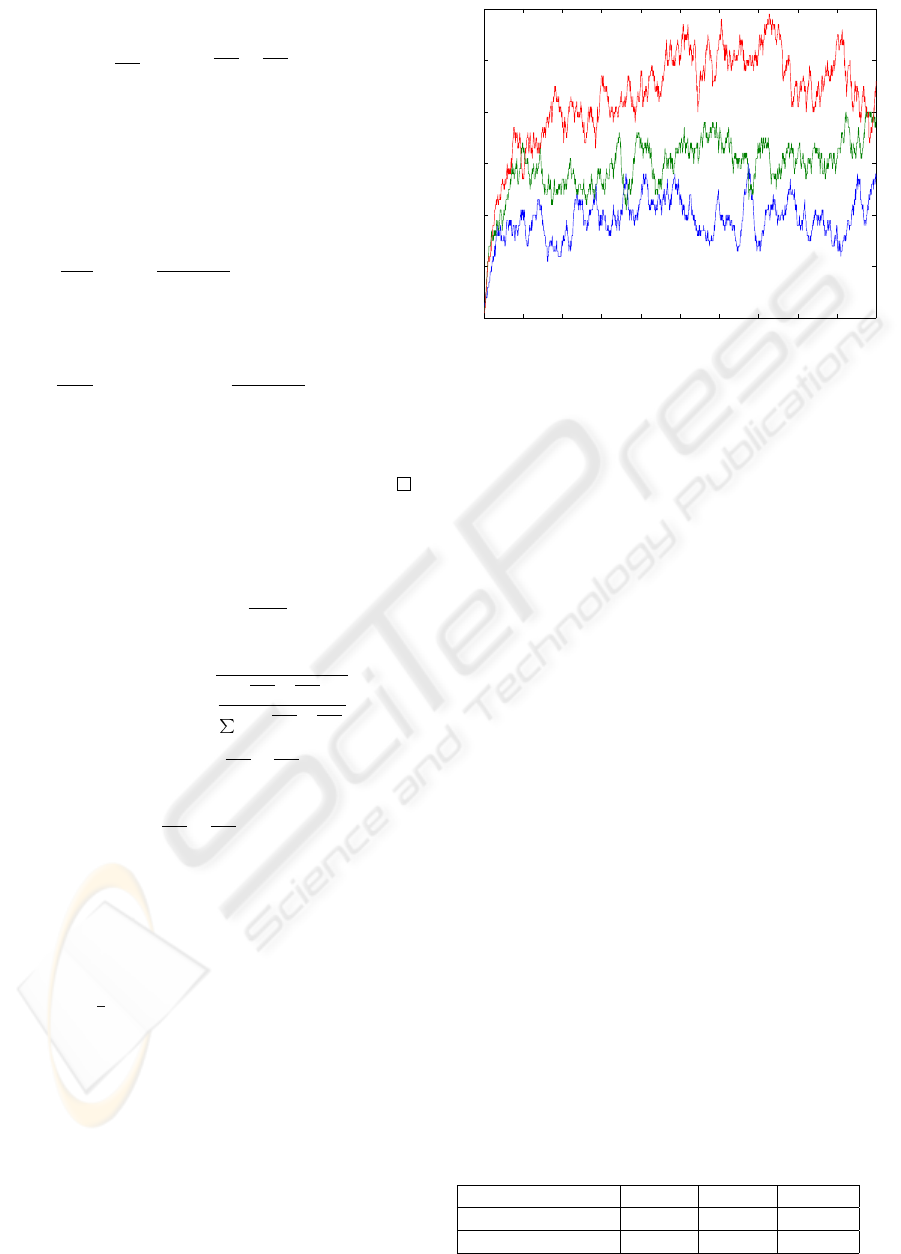
Figure 1: Evolution of the number of connections as a func-

tion of time.

= 0.011, where the probability density functions

for the durations are

(t) = β

−β

, , i = 1, 2, 3 t ≥ 0. (18)

The number of unit times in the experiments was τ =

2000 which is 2 seconds using T as deﬁned above. In

the experiments the pricing factors r

= 0 as they only

make a shift in the revenue curves (i.e. increase the

revenues). The penalty factors were chosen as s

10, s

= 15 and s

= 20 for gold, silver and bronze

classes, respectively. So connections causing delay in

the gold class are penalized less and those in bronze

class the most.

The number of connections on the average is high-

est for the bronze class and lowest for the gold class

as is seen in Fig. 1. The number of connections also

varies greatly over time. Each connection has con-

stant value of 1 to 5 packets in the queue during their

life time. The delays for the services classes when

using constant weights are shown in Fig. 2. It is ob-

served that the delays remain quite constant because

the weights are constant. By using adaptive weights a

delay critical class used for e.g. real time trafﬁc can

be favored with respect to delay. In the experiment

the parameters s

were chosen so that with adaptive

weights the gold class customers get less delay with

the expense of the other classes (Fig. 4). By adjusting

the penalty factors s

the relative delays between the

classes can be adjusted. The values of mean delays

Table 1: Mean delays of gold, silver and bronze class for

the constant and adaptive weight algorithms.

Mean delays [s] Gold Silver Bronze

Constant weights 0.1133 0.2642 0.7712

Adaptive weights 0.0804 0.4475 1.7155

PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY

115

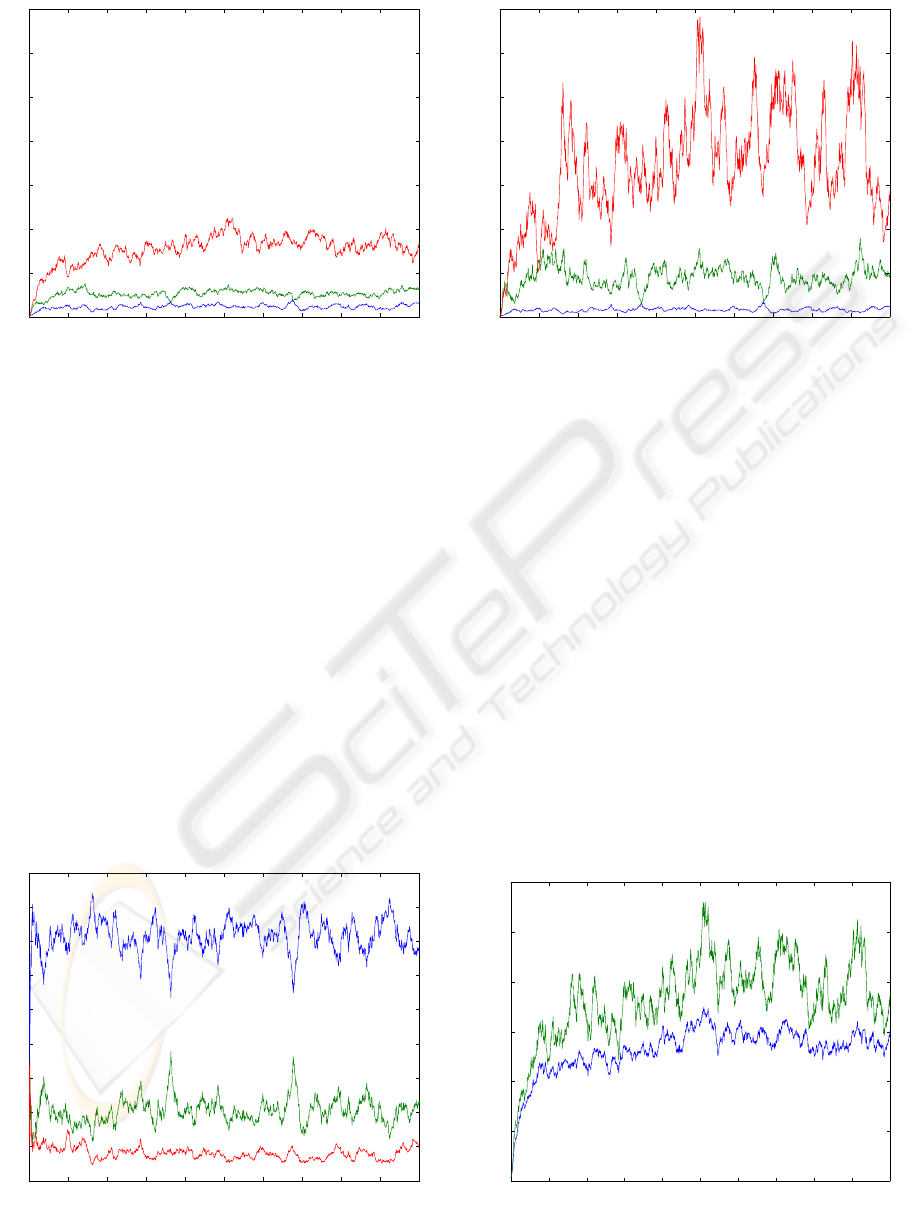
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

0.5

1.5

2.5

3.5

Time[s]

Delay[s]

Bronze

Silver

Gold

Figure 2: Constant weights - Evolution of the delay as a

function of time.

for the classes in both cases are seen In Table 1.

The adaptive weights are seen in Fig. 3 and the

total revenues for both versions of the algorithm is

seen in Fig. 5. Mean revenues in case of con-

stant weights was 5273.9 and in the case of optimal

adaptive weights 7297.0. The adaptive weights give

greater total revenue and smaller delay for the gold

class.

4 DISCUSSION

In this section, we discuss the algorithm from the

point of view of theory and experiments. Analytic

forms of the revenue and the weights, that allocate

trafﬁc to the connections of different service classes

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Bronze

Silver

Gold

Time[s]

Figure 3: Evolution of the weights w as a function of time.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

0.5

1.5

2.5

3.5

Time[s]

Delay[s]

Bronze

Silver

Gold

Figure 4: Adaptive weights - Evolution of the delay as a

function of time.

were deﬁned. The updating procedure is determinis-

tic and nonparametric i.e. it does not make any as-

sumptions of the statistical behavior of the trafﬁc and

connections. Thus it is robust against the errors that

may occur from erroneous models. The algorithm

is unique and optimal, which has been theoretically

proved by Lagrangian optimization method. Closed

form solution makes the algorithm quite simple. By

changing the penalty factor s

of one class higher,

the delays in other classes are decreased. Because all

penalty factors s

are positive, all classes obtain ser-

vice in fair way. The method always optimizes the

operator’s revenue and by knowing what kind of traf-

ﬁc is in different service classes the parameters can

be set so that the delay for delay critical trafﬁc can

be maintained low enough. A call admission control

mechanism could also be implemented to assure def-

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

2000

4000

6000

8000

10000

12000

Time[s]

Revenue

Optimal

Constant

Figure 5: Evolution of the revenue R as a function of time.

ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS

116

inite delay limits in cases the network load increases

too much. As the delays grow the operators revenue

increases, but it cannot increase to inﬁnity in reality.

This is because when the buffers get full and pack-

ets start to drop, connections drop also at some point.

A penalty term for the operator is under study, which

would lower the price when there is too much delay.

5 CONCLUSION

In this paper an adaptive algorithm for optimizing

the network operator revenue and ensuring delay as

a Quality of Service (QoS) requirement was pre-

sented. The closed form algorithm was derived from

a revenue-based optimization problem. The pricing

of the connection is based on the delay that it in-

ﬂicts on other connections. The customers that in-

duce most delay to the network by large amounts of

trafﬁc are charged the most. In the experiments we

simulated the operation of the adaptive algorithm and

compared it with a constant weight version of the

same algorithm. The obtained results show that by

using the adaptive weights the delays can be adjusted

so that the users is different QoS classes are content.

With the constant weights, the delays cannot be con-

trolled. Also, the revenue is maximized while ensur-

ing that the customers delays stay small according to

the their class. The algorithm is deterministic and

non-parametric, and thus in practical environments it

is a competitive candidate due to its robustness. Fu-

ture work shall concentrate on expanding the idea to

several nodes with more QoS parameters.

REFERENCES

Bennett, J. C. R. and Zhang, H. (1996). WF

Q: worst-

case fair weighted fair queueing. In Proc. 15th Annual

Joint Conference of the IEEE Computer and Commu-

nications Societies (INFOCOM’96), volume 1, pages

120 – 128.

Demers, A., Keshav, S., and Shenker, S. (1989). Analy-

sis and simulation of a fair queuing algorithm. ACM

SIGCOMM Comput. Commun. Rev., 19(4):1–12.

Golestani, S. J. (1994). A self-clocked fair queueing scheme

for broadband applications. In Proc. 13th Annual Joint

Conference of the IEEE Computer and Communica-

tions Societies (INFOCOM’94), volume 2, pages 636

– 646.

Goyal, P., Vin, H. M., and Cheng, H. (1997). Start-time fair

queueing: a scheduling algorithm for integrated ser-

vices packet switching networks. IEEE/ACM Trans.

Networking, 5(5):690–704.

Guo, C. (2001). SRR: an O(1) time complexity packet

scheduler for ﬂows in multi-service packet networks.

ACM SIGCOMM Comput. Commun. Rev., 31(4):211–

222.

Joutsensalo, J., Viinikainen, A., Hämäläinen, T., and Wik-

ström, M. (2005). Bandwidth allocation and pricing

for telecommunications network. In Proc. Next Gen-

eration Internet Networks (NGI’05), pages 165 – 172.

Kanhere, S. S. and Sethu, H. (2001). Fair, efﬁcient and low-

latency packet scheduling using nested deﬁcit round

robin. In Proc. IEEE Workshop on High Performance

Switching and Routing, pages 6 – 10.

Kanhere, S. S., Sethu, H., and Parekh, A. B. (2002). Fair

and efﬁcient packet scheduling using elastic round

robin. IEEE Trans. Parallel Distrib. Syst., 13(3):324–

336.

Marosits, T., Molnár, S., and Sztrik, J. (2001). CAC algo-

rithm based on advanced round robin method for QoS

networks. In Proc. Sixth IEEE Symposium on Com-

puters and Communications, 2001, volume 2, pages

266 – 274.

Parekh, A. K. and Gallager, R. G. (1993). A general-

ized processor sharing approach to ﬂow control in

integrated services networks: The single-node case.

IEEE/ACM Trans. Networking, 1(3):344–357.

Ramabhadran, S. and Pasquale, J. (2003). Stratiﬁed round

robin: A low complexity packet scheduler with band-

width fairness and bounded delay. In Proc. 2003 con-

ference on Applications, technologies, architectures,

and protocols for computer communications, pages

239 – 250. ACM Press.

Shreedhar, M. and Varghese, G. (1996). Efﬁcient fair queu-

ing using deﬁcit round-robin. IEEE/ACM Trans. Net-

working, 4(3):375–385.

Stiliadis, D. and Varma, A. (1998). Efﬁcient fair queueing

algorithms for packet-switched networks. IEEE/ACM

Trans. Networking, 6(2):175–185.

Tsao, S.-C. and Lin, Y.-D. (2001). Pre-order deﬁcit

round robin: a new scheduling algorithm for packet-

switched networks. Comput. Networks, 35(2-3):287–

305.

Viinikainen, A., Joutsensalo, J., Pääkkönen, M., and

Hämäläinen, T. (2004). Packet scheduling algorithm

with weight optimization. In Proc. International Con-

ference on E-business and Telecommunication Net-

works (ICETE’04), volume 2, pages 127 – 133.

Yuan, X. and Duan, Z. (2005). FRR: a proportional

and worst-case fair round robin scheduler. In Proc.

24th Annual Joint Conference of the IEEE Computer

and Communications Societies (INFOCOM’05), vol-

ume 2, pages 831– 842.

PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY

117