MODELING THE DYNAMICS OF SOCIAL NETWORKS

Victor V. Kryssanov, Frank J. Rinaldo

Faculty of Information Science and Engineering, Ritsumeikan University, Kusatsu, Shiga, Japan

Evgeny L. Kuleshov

Department of Computer Systems, the Far-Eastern National University, Vladivostok, Russia

Hitoshi Ogawa

Department of Information and Communication Science, Ritsumeikan University, Kusatsu, Shiga, Japan

Keywords: Social networks, Power law, Human response time, Consumer behavior.

Abstract: Modeling human dynamics responsible for the formation and evolution of the so-called social networks –

structures comprised of individuals or organizations and indicating connectivities existing in a community –

is a topic recently attracting a significant research interest. It has been claimed that these dynamics are

scale-free in many practically important cases, such as impersonal and personal communication, auctioning

in a market, accessing sites on the WWW, etc., and that human response times thus conform to the power

law. While a certain amount of progress has recently been achieved in predicting the general response rate

of a human population, existing formal theories of human behavior can hardly be found satisfactory to

accommodate and comprehensively explain the scaling observed in social networks. In the presented study,

a novel system-theoretic modeling approach is proposed and successfully applied to determine important

characteristics of a communication network and to analyze consumer behavior on the WWW.

1 INTRODUCTION

Understanding the mechanisms underlying the

formation and evolution of social (communication,

entertainment, financial, and the like) networks is

crucial in many fields of human activity, ranging

from software development, to market analysis,

resource distribution and deployment, and to

catastrophe prognosis and prevention (see Newman,

2005, for a comprehensive survey). Recently, there

is an increasing number of reports that the dynamics

of social networks reveal statistical properties

conforming to the power law (Johansen, 2004;

Barabasi, 2005; Oliveira and Barabasi, 2005;

Adamic and Huberman, 2000; Scalas et al., 2006).

Striving to find a universal model for the human

behavior apparently responsible for the observed

statistics, researchers have been quick to affiliate

social networks with the familiar Zipfian phenomena

(Newman, 2005; Barabasi and Albert, 1999).

There exist a rich variety of stochastic processes

leading to a power, heavy-tailed (e.g. Zipf, Zipf-

Mandelbrot, or Pareto) form of the probability

distribution of an observed random variable

(Mitzenmacher, 2003). Only a small fraction of

these processes, however, would be considered

relevant to discuss in a social, economic, or

anthropological context peculiar to the development

of social networks. Even fewer processes have

actually been explored as possible generating

mechanisms for the network dynamics and tested

against real-world data.

Adamic and Huberman (2000) gave an

explanation for the power-law distribution of the

consumer activities in a global e-market, such as the

World-Wide Web (WWW). The proposed model

exercises the well-studied multiplicative growth

stochastic mechanism for the network expansion but

carries no implication about the human behavior.

Barabasi (2005) suggested a version of the

preferential selection mechanism to describe the

242

V. Kryssanov V., J. Rinaldo F., L. Kuleshov E. and Ogawa H. (2006).

MODELING THE DYNAMICS OF SOCIAL NETWORKS.

In Proceedings of the International Conference on e-Business, pages 242-249

DOI: 10.5220/0001425402420249

 SciTePress

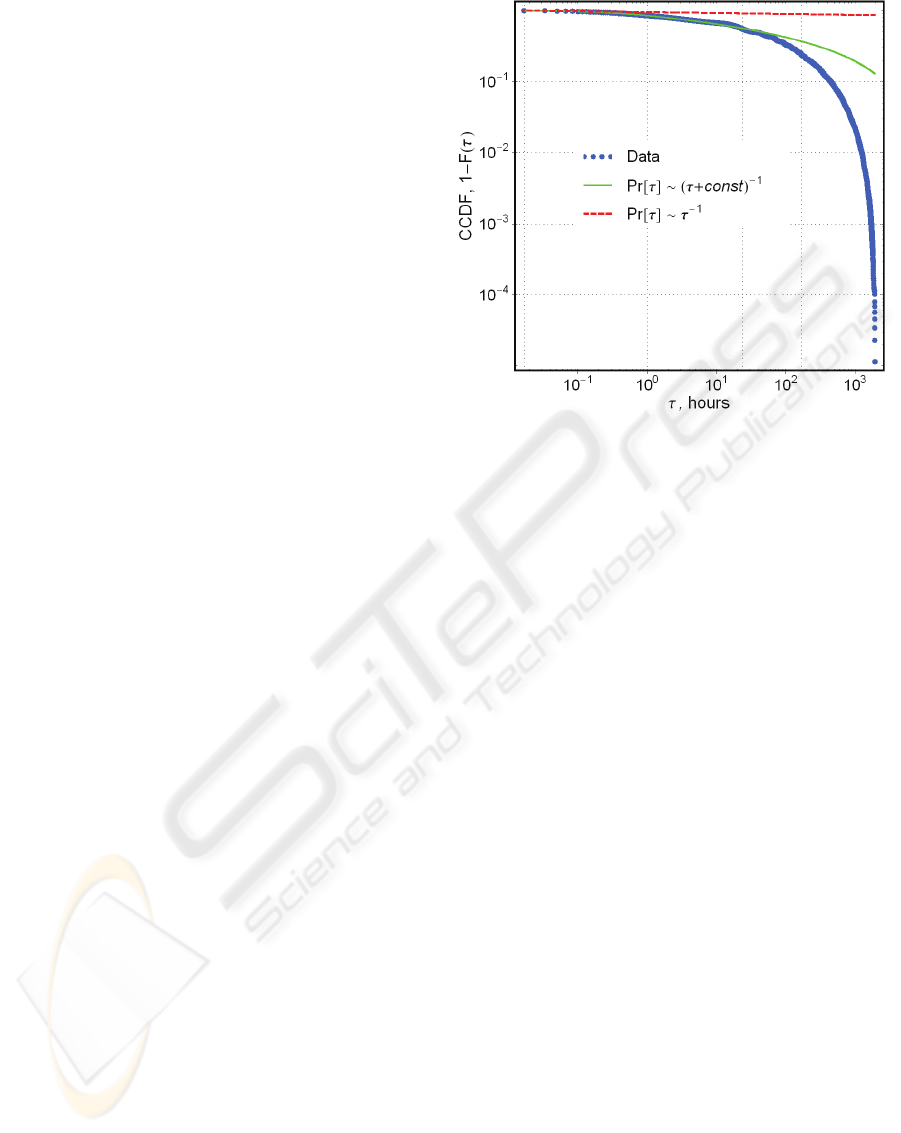
dynamics observed in a university e-mail network.

While he did propose a model for human

communicative behavior, which is, effectively,

choice based on priorities, this model requires

making rather implausible assumptions (e.g. about

uniformly distributed priorities) and yet

demonstrates poor predictive results even for the

data originally used in the study (see Figure 1; also

Stouffer et al., 2005). Johansen (2004) derived an

empirical formula, which provides a good

approximation for the general response rate of a

human population, working with the same data as

the previous author (Figure 1). Another example of

the empirically grounded approaches to modeling

the dynamics of social networks is a modification of

the Zipf-Mandelbrot law – the formula suggested by

Krashakov et al. (2006) to characterize the

popularity of Web-sites that apparently has a

predictive power better than the classic (e.g. the

“pure” power or Zipf law) models. The latter two

studies, however natural, offer little insight on why

the observed networks exhibit scale-free properties.

In the absence of a sufficiently universal

alternative to the power law (see Solow et al., 2003,

for a relevant discussion), the above mini-survey is

quite indicative of the current situation with the

understanding and modeling of the dynamics of

social networks. Whenever the true mechanism

underlying the observations is not known, the most

probable scenario is that any process generating

heavy-tailed data is either “by default” (i.e. with a

minimal, if any, attention to statistical hypothesis

testing and model validation) attributed to (a version

of) one of the well-studied power-law generating

mechanisms, such as multiplicative growth,

preferential attachment, optimal coding, etc. or

simply approximated with an empirical “a la Zipf”

formula having an arbitrary interpretation that can

hardly be discussed in a context different from mere

curve fitting.

In the presented study, the authors aim to

improve upon this, in essence theoretical, deficiency

and focus on the development of a reasonably

universal approach that would provide a distinct

modeling perspective and have a potential to deliver

a plausible and verifiable explanation of scale-free

phenomena discovered in diverse social networks.

The next section gives a general mathematical

framework. It is applied to analyze possible reasons

of the power law patterns in the observed behavior

of complex systems. Two experiments are then

conducted to determine the dynamic structure of

social networks, based on the proposed theory, and

their results are briefly discussed. The study’s

conclusions are drawn, and plans for future research

are outlined.

2 SYSTEM-THEORETIC

FRAMEWORK

In this section, we will analyze the observed

behavior of the so-called complex systems – the

conglomerates (physical, social, cognitive,

cybernetic, or the like) whose internal mechanisms

and structure by some reason cannot be inspected in

full. Power-law phenomena are very often associated

with (produced by, observed in, etc.) such systems.

Let us consider a system

Ω defined in a very

general sense, i.e. as the object of investigation (not

necessarily physically grounded). An observable

is a property of the system

Ω that can be

investigated in a given context. We will assume that

exists in different states and that different states

of the system release themselves as different

outcomes of observations (measurements, etc.)

associated with observables

O . The latter means

that the system states (or behavior, seen as state

Figure 1: Problems with explaining the heavy-taile

activity pattern in e-mail communications: While the

empirical formula (solid line) derived by Johansen (2004)

provides a better approximation for the distribution of

the time taken by an individual to reply to a received e-

mail, than Barabasi’s model (dashed line) based on a

activity-

rioritizing mechanism (Barabasi, 2005), it gives

no clue about the generating process. (For details on the

data, see Eckmann et al., 2004.).

MODELING THE DYNAMICS OF SOCIAL NETWORKS

243

change) are in principle conceivable through their

representations resulting from observations of

O .

We will seek to determine the distribution of the

occurrence number of different representations

associated with a given observable across increasing

expenditures of time. In so doing, we will assume

that a) the same state can have different

representations, and b) different states can have the

same representation. The analysis will be in three

steps.

Step I: to characterize the occurrence number (or

rate) of different representations of one (identical)

state for the same observable

O .

Case 1

: Let the process of system state

representation implement an efficient encoding

procedure so that

consttk

, where

k is the

expectation of a discrete random variable

revealing the occurrence number of different

representations, and

t is the average time of state

representation.

To estimate

)(

the probability mass

function (PMF) of

K , we will maximize its

entropy

)(ln)(

sfsfH

KKs

Σ−=

, …,2,1=s ,

subject to constraints

1)(

=Σ sf

and

)(

ksfs

=Σ . This will give us “the least biased

estimate possible on the given information” (Jaynes,

1957).

The optimization problem is solved using a

Lagrangian approach. The Lagrangian function is

defined as

,))((

))(1()(ln)()(

0000

∑

∑∑

−+

−+−=

KKK

sfsk

sfsfsff

(1)

where

and

are coefficients, with optimality

conditions

0)(

=∂∂ sf

, 0=∂∂

L/ , and

0=∂∂

L/ (Cover and Thomas, 1991). From the

first and second conditions, one can then derive

λλ

eesKsf

−

−=== )1(]|Pr[)(

, (2)

where

…,2,1=s . Since

∑

∞

)(

sfsk

)1(/1)1/(

fee =−

λλ

and 1

>>k ,

1)1(

and

1<<

, and therefore

/1 k≈

Case 2

: Let us now consider a different-type

system and impose a conservation constraint for the

representation (observation) time by requiring that at

any time, only one but not necessarily the same

property of the system is evaluated. In other words,

we will assume that there are multiple competing

observables for the same state. We will also assume

that these observables are independent. (To simplify

technicalities, the following discussion will mainly

be built around the continuous case, i.e. for

k the

continuous counterpart of

K , yet with the

customary abuse of the notation when the same

symbol is used to refer to a random variable and to

its value.)

For

a period of time,

w the rate of the

representation change is given as

kw = .

Under the above assumptions, the dynamics of

can be modeled using a system of differential

equations defined as follows:

ημρ

⎟

⎠

⎞

⎜

⎝

⎛

−=

∑

(3)

where

is the investigated state rate (characterizes

the “true,” as opposed to the observed, behavior of

the system),

N is the number of competing

observables,

Ni ...,,1,0

; )(t

is a Gaussian noise

(e.g. due to measurement errors) with average zero,

some

0)( >ta

, and

is a parameter to account for

the efficiency of the representation process (i.e. the

system state may principally be only to an extent

available for observation).

Equations (3) describe a diffusion process in the

vicinity of a hyperplane

Σ=

ρμ

formed by

N observables with

w representation rates,

whose values are (approximately) uniformly

distributed in the interval

],0[

ρμ

. Due to the

hyperplane condition, there can be only

N mutually

independent observables, say

OO ...,,

by definition. The probability

that

≥ , Nn ...,,1

, can be calculated as a

product of the marginal distributions

1)(

kf , that then yields

kkkkk )1(]...,,Pr[

0001

θρμ

−=≥≥ . Probability

theory defines the cumulative distribution function

(CDF) for some

x taken from the set of all random

variables that obey a given probabilistic law as

],,Pr[)(

0010

xxxxxF

… . In this context and

for

1>>N , one can write:

ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS

244

θρμ

1)1(1)(

ekkF

−

−≈−−∝

, (4)

where parameter

)(

−

′

ρθλ

t is, up to the constant

1 , determined by

))1/((

−

′

the

representation time averaged over the observables

(note that generally,

t of Case 1 is not equal to

′

At this point, we would like to note that while there

would be a number of modeling scenarios both,

similar to and different from those of Case 1 and 2,

which would produce an exponential form for the

distribution sought, the approaches discussed above

have two important implications. First, the models

defined with Equations (2) and (4) both stipulate that

under other similar conditions, more often met

representations correspond, on average, to system

states with a shorter representation time. Second, for

an occurrence number significantly greater than 1,

the parameter

1<<

Step 2: to characterize )(tk the representation

occurrence number of many different states for the

same observable

O .

For the system

Ω , the measured stochastic

variable

k will be a sum of random variables

...21

000

+++ kkk , where the summands are due to

different states having identical representations. The

statistical properties of

k will then depend on the

parameter

that can naturally vary (e.g. as a result

of a variation in the average representation time for

different states). Let

)(

be the probability density

function (PDF) of

. For a large number of states

investigated by means of

O , )(kf the PDF of k

is defined as a

)(

g parameter-mix of

)|(

=Λkf :

∫

∞

==Λ= ∧

)()()()|()(

λλλλ

dkPggkfkf , (5)

where

)(

kP is the PDF of

k discussed in Step 1.

Step 3: to generalize the result of Step 2.

The random variable

k may reflect more than

one (presumably associated with the observable

O )

property of the system

Ω , while the system

mechanisms controlling the observable may be

heterogeneous in time (e.g. owing to environmental

perturbations). This can provoke the existence of

more than one probability distributions for

. When

the number of statistically independent factors

influencing the observation (or the system behavior)

is finite,

)(kP

the PDF of the occurrence number of

system state representations can be estimated as

∑

kfckP

)()( , (6)

where weights

c give the likelihood to observe the

influence of the i-th factor on the random variable

k , and each )(kf

is specified with Equation (5)

and is determined by the (sub)system parameters as

it was discussed in Step 1.

3 WHEN THE POWER LAW?

The analytic framework formulated in the previous

section is fairly general and can be applied to

analyze the behavior of virtually any complex

system. It should be emphasized however, that the

focus of the developed model is on the frequency

(count) of observed activities rather than on their

durations. Most of the modeling approaches

discussed in the introduction are therefore not

directly comparable to the one proposed in this

study. Given the fact that in social systems, there

often exists a detectable (though not always easily

formalizable) connection between the frequency of a

certain activity and its duration, it appears

interesting to explore under what conditions

Equation (6) may produce a power form of the

probability distribution.

An acute reader would have already noticed that

the substitution of the exponential PDF into

Equation (5) yields a Laplace transform of the

product

)(

g :

∫

∞

−

)()(

λλ

dGekf

, (7)

where

)(

G is the CDF of

This is a very nice result since it, owing to

Bernstein’s theorem (Bernstein, 1928), stipulates

that if

)(kf

, the PDF of the observed variable, is

completely monotone, i.e. all its derivatives exist

and

0)()1(

)(

≥− kf

for any integer 0>k and

1≥n , there can always be found some proper )(

in effect describing the internal (i.e. not directly

observed, “true”) dynamics of the system. There is a

large class of probability distributions for

(e.g.

originated from or simply approximated with the

Beta of the Second Kind probability distribution

MODELING THE DYNAMICS OF SOCIAL NETWORKS

245

)(1

)1())()(/)(()(

qpp

qpqpg

+−−

+ΓΓ+Γ=

λλλ

where

)(⋅Γ denotes the Gamma function, 0>p and

0>q are parameters, which encompasses many

commonly used distributions, such as the Log-

Normal, Gamma, Weibull, etc. – see McDonald and

Xu, 1995) that will cause “fat” tails of the observed

data

−

∝ kkf )( for some 0>

∞

→k (Abate

and Whitt, 1999). This asymptotic property will,

however, not necessarily be maintained for small

k .

Generally, the developed model dictates that in

the case of a homogeneous (i.e. assuming the

existence of one PDF

)(

) system, candidate

distribution functions for the description of the

statistical properties of

k and

should satisfy

Equation (7). In view of this, an interesting exercise

would be to find a family of probability functions

satisfying the Laplace transform (7). Unfortunately,

no closed analytic forms for

)(

g exist in many

cases of long-tailed

)(kf

Equation (6) further stipulates that in order for

−

∝ kkP )( , either all the summands should have

an identical “heavy-tailed” form (that would indicate

certain self-similarity existing in the system) or at

least one of the summands should have a power

form with an exponent

small enough to

dominate the asymptotic behavior of the other

distributions.

4 MODELING THE DYNAMICS

OF SOCIAL NETWORKS

To verify the proposed model against real-world

data and explore its predictive and analytic

capabilities, two experiments have been conducted.

4.1 Experiment 1

Data used in the experiment is a sample representing

the timing of e-mails sent and received by a group of

~10000 people at a university in Europe during a

period of ~80 days. The corresponding server log-

file was obtained from the authors of Reference

(Eckmann et al., 2004). Specifically, we have

focused on the time taken by an individual to reply

to a received message – the human response rate;

there have been extracted ~24000 of reply times

from the file. It was reported elsewhere (Eckmann et

al., 2004; Johansen, 2004; Barabasi, 2005) that

power-law generating mechanisms could be behind

the formation of the distribution of this data, as it

exposes the characteristic (yet noisy) heavy-tailed

pattern (see Figure 1; also the inset in Figure 2).

The discretization time interval for the delays

with reply was set to 1 minute. No other

preprocessing has been done. The investigated

system in this case is the social system that existed

at the university, and the observed property is the

perturbed (by incoming e-mails) communication

timing. It is expected that delays with reply to

received e-mails reveal the rate of the system

internal state change (e.g. in its simplest form, from

“e-mail is not replied” to “e-mail replied”).

The two-parameter Gamma distribution

)(/)(

νλλ

λνν

Γ=

−− b

ebg , where 0≥

, 0>b ,

, and )(

⋅

denotes the Gamma function, was

chosen to characterize the system’s hidden

dynamics, because this is a simple form well

describing cognitive processes and “mental” reaction

time (Luce, 1986). This form can, and possibly

should, be considered for

)(

g regardless what is

the “true” mental architecture triggering one or

another investigated human activity (van Zandt and

Ratcliff, 1995). Taking into account the discrete

nature of the observed variable value count and after

substitution of the corresponding PMF and PDF into

Equation (5), Equation (6) is specialized to

...,2,1,

)()1(

)(

⎟

⎠

⎞

⎜

⎝

⎛

−

+−

∑

ckP

(8)

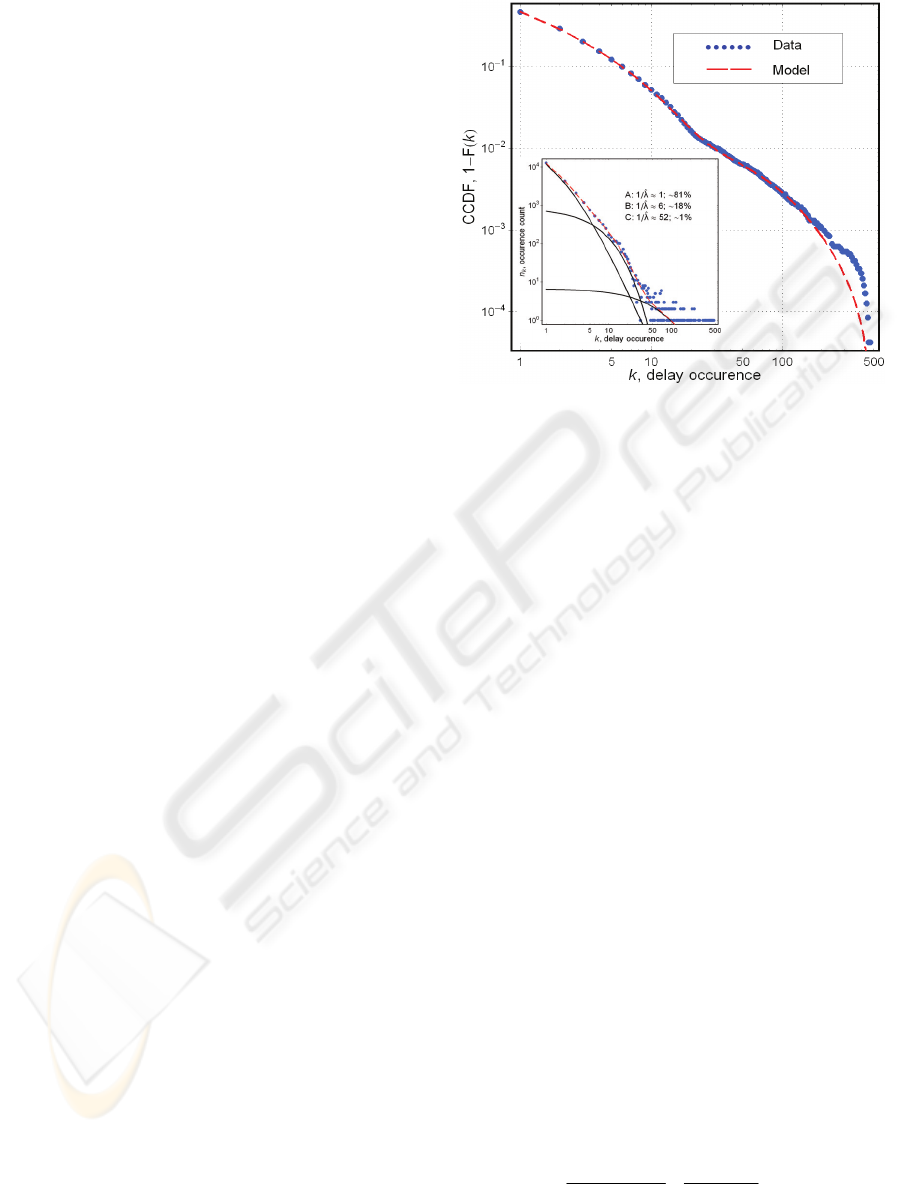
Figure 2: Estimation of the dynamic social structure base

on an analysis of the traffic in a university e-mail network.

ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS

246

that is thus the probability mass function of the

occurrence of a human response rate. Note that each

of the summands has the form of the discrete Lomax

distribution.

Figure 2 depicts the complementary cumulative

sums calculated for the data and the model (8) with

parameters

c ,

b and

obtained by a numerical

maximum likelihood method and

3=M as yielding

the smallest value of Akaike’s Information Criterion,

nxL 2))|

(log(2AIC +−=

, where ))|

(log( xL

the log-likelihood maximized with parameters

(for the PMF (8),

Mibc

iii

...,,1},

{

≠

νφ

) for a

given sample

, and n is the number of estimable

parameters (for

3=M , 8=n ). AIC is a

fundamental measure assessing the relative

Kullback-Leibler distance between the fitted model

and the unknown true mechanism, which actually

generated the observed data (Akaike, 1983). Taking

into account the information known from the

original report (Eckmann et al., 2004) about the

structure of the social system in focus, models with

the number of components ranging from 1 to 4

have been tried in the experiment. The second-best

model had

, 5=n and was therefore simpler,

but with an

AIC value by 90 greater than in the case

3=M it had to be omitted from further

consideration (Sakamoto et al., 1986).

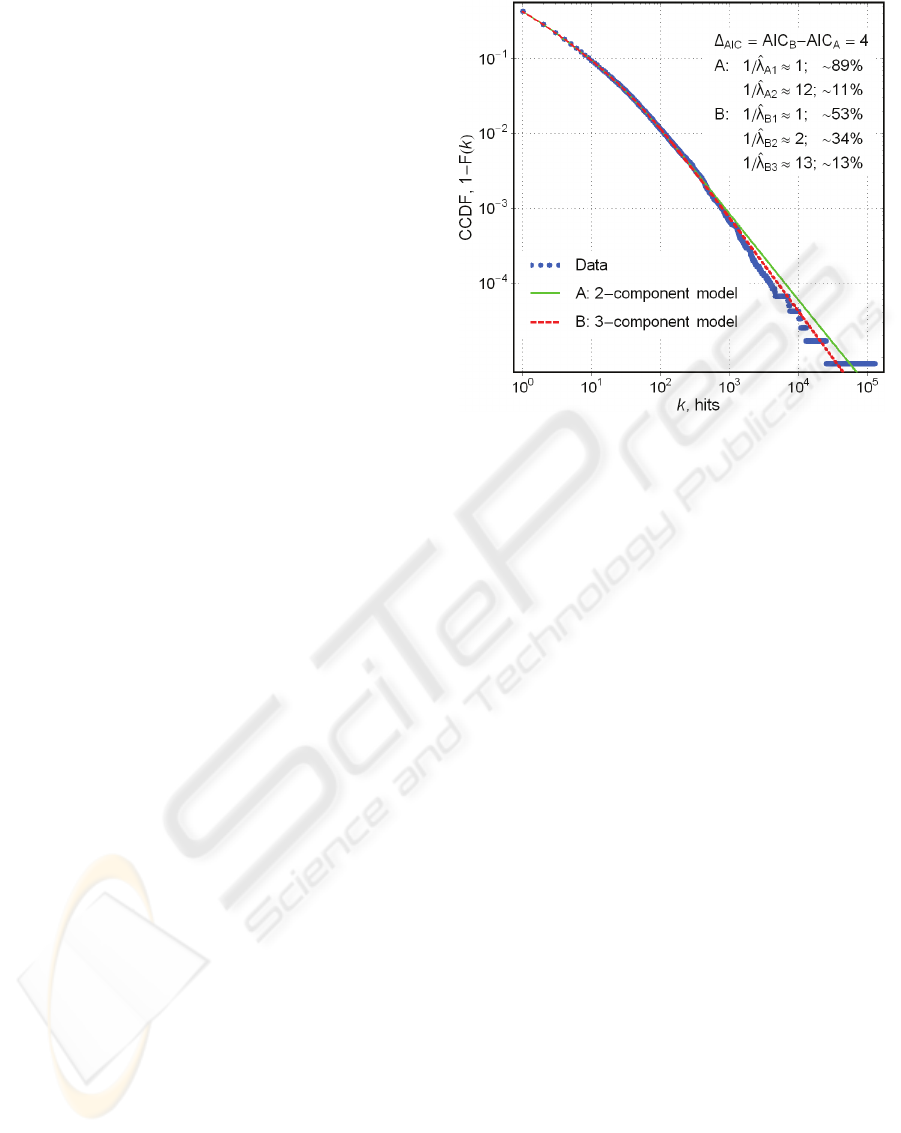
4.2 Experiment 2

To explore the dynamic structure of an e-market on

the World-Wide Web, a data sample representing

the activity of America Online (AOL) users (acting

as consumers of the services provided by Web sites)

has been obtained from the authors of Reference

(Adamic and Huberman, 2000). The sample covers

approximately 120000 sites accessed by 60000 users

during one day.

Figure 3 shows the results of the modeling of the

consumer activity dynamics with formula (8). It is

assumed that a hit to a particular site corresponds to

a specific mental or “goal” state, and that these

states are common (i.e. shared) within the population

(from a generic anthropological viewpoint, this

seems a natural assumption). As no a priori

information was available on the structure of the

social system examined, four prediction models have

been probed by varying the value of

from 1 to 4.

The two models displayed in the figure are

statistically justified by the data and perform

practically equally well.

5 DISCUSSION

It is quite illustrative that while a “pure” form of the

power law would fail to reasonably accurately

predict probabilities for the entire ranges of the data

used in the experiments, as the corresponding

complementary cumulative sums visibly do not form

single straight lines on the double-logarithmic plots,

the model specified with Equation (8) produces

sound fits.

For the university e-mail network, Pearson’s

test does not reject the model with a significance

level

001.0

that might be considered good

enough in the case of noisy data. An objection

would, however, be made that the proposed model

overfits the data: the large number of its parameters

creates a situation when the fit may be driven by the

random fluctuations rather than by the “true”

statistical properties of the data.

The values of

c the parameters obtained in the

first experiment suggest that the examined social

system has an internal structure: there are two

subsystems with different dynamics responsible for

the generation of approximately 81 and 18% of the

observed variety in delays with reply to an e-mail;

about 1% of the occurrences – for the most typical

and shortest delays – are probably caused by factors

other than social (e.g. owing to an auto-reply

Figure 3: Modeling the Web site (server) visiting rate

(hits) observed on December 1, 1997, in a segment of the

WWW. (For details on the data, see Adamic an

Huberman, 2000.).

MODELING THE DYNAMICS OF SOCIAL NETWORKS

247

function of the e-mail clients or the processing of

long mailing lists) and may be excluded from

consideration.

The larger, “static” subsystem –

A in the inset of

Figure 2, where the distributions are built for the

data, the model, and the model’s 3 components –

produces on average longer yet unique delays (for a

gamma-distributed

, the estimate of its mean

). The second subsystem – B – is

approximately 4 times smaller (or 4 times

observationally less influential) and 6 times more

dynamic (and hence, as it could be speculated, is

more constrained and/or has stronger social ties).

These size estimates principally conform to the ones

reported in the original work (Eckmann

et al., 2004)

and independently obtained through somewhat

intricate analysis of the individual communications

present in the sample. This, along with the fact that

the obtained parameters behave just as it is implied

by the model (back to Section 2), can be considered

as strong evidence in support of the hypothesis that

Equation (8) does describe the system behavior but

not merely approximates the data.

In the second experiment, the models with two

and three Lomax-distributed components are not

rejected by Pearson’s test with

1.0=

. The

difference in

AIC calculated for these models

implies that neither should be favored in the absence

of information other than obtained from the data.

Nevertheless, both of them suggest that

approximately 10% of the observed variety in the

site popularity is due to mental states (and

corresponding activities) most often experienced

(pursued) by the consumers at the e-market. The

latter does not appear implausible in the light of the

Internet demographic survey for 1997 by Nielson

Media Research (http://www.nielsenmedia.com

)

stating that 73% of the consumers used the WWW to

search for information about products and services

by means of accessing a small number of Web

portals and search engines, such as Yahoo

, etc.

It is understood that for any “complete”

validation of the proposed model, many more

experiments are required but are beyond the limits of

this paper. Additional cross-checking and

verification are, however, still indispensable because

technically, derivation of the Lomax (Pareto Second

Kind or General Pareto) distribution as a gamma

mix of exponentials was first reported several

decades ago (Harris, 1968) but did not receive due

attention in complex system research.

One supportive argument for the proposed

approach is that it does not contradict the findings

about the dynamics of social networks reported in

the literature, but instead generalizes them. The

widely held form of the power law

/)(

νν

kbkP can be obtained from Equation (8)

for

bk >> by Taylor series expansion (the minuend

– by small

kb /)1(

−

, and the subtrahend – by small

kb / ) under the assumption that the investigated

system is homogeneous (i.e. by setting

Let us now consider an asymptotic

approximation of the model, which is also the

continuous counterpart of Equation (8):

)()(

−−

bkbkP

. (9)

From

∫

∞

−

+==

xbbldkkPlxR

νν

)()()( , (10)

where

)(xR gives

the rank of a unit of size

)()()2()1( lr

xxxx ≥≥≥≥≥ 

, in a set of

objects, one can easily obtain

1/1/11 −−+−

−= lbrlbf

νν

, (11)

where

f is the relative occurrence frequency of the

r-th popular unit. When

, this result coincides

with the empirical formula

−

++= )( ruqdf

, d,

q, and u are some constants, obtained by the authors

of Reference (Krashakov

et al., 2006). Moreover,

the negative values of

d empirically calculated in the

latter study are generally in agreement with what

would be estimated based on the sample size by

applying formula (11), where

0, >lb by definition.

As a final remark, let us mention that a

lognormal distribution is often discussed as an

alternative to the power law when describing the

dynamics of complex systems (Mitzenmacher, 2003;

Stouffer

et al., 2005). Given bk >> and some m,

km ln2 >> , Equation (8) can be approximated as

)(ln

)(

−

= (12)

that gives its lognormal asymptotic form.

6 CONCLUSIONS

Having defined the overall goal as to deliver a

universal but simple and accurate theoretical model

for the observed behavior of a large class of complex

systems, in this particular paper we focused on the

ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS

248

formation of the dynamics of social networks and on

methods for the network structure analysis. A

mathematical model correctly describing these

phenomena would help optimize resource and

service allocation as well as economic and

management policies for companies in both the

traditional and electronic business sectors, and also

for organizations involved in collaborative activities,

such as distribution of funds, innovation and know-

how exchange, and so on.

We have applied the apparatus of statistical

physics to describe the emergence of social

networks. The network dynamics was defined in

terms of its structure (i.e. how many subsystems are

there and what is, as observed, their influence on the

overall dynamics) as well as parameters of its

elementary constituents (these parameters are the

mental reaction time and, possibly, response times of

external systems coupled with or simply affecting

the social network). In the presented experiments,

the proposed model has demonstrated a prognostic

potential far superior to any of the classical

modeling approaches. At the same time, the model

proved to be quite encompassing but natural and

thus easy to interpret and validate.

In our prior research reported elsewhere, the

system-theoretic framework was successfully

applied to capture the structure of different

languages and to compare the efficiencies of text-

and hypermedia- based communication (Kuleshov

., 2005; Kryssanov et al., 2005). In future studies,

we plan to explore various authorship networks.

ACKNOWLEDGEMENTS

The authors would like to thank, without

implicating, Lada A. Adamic and Jean-Pierre

Eckmann for providing the data used in the research.

REFERENCES

Abate, J. and Whitt, W., 1999. Modeling service-time

distributions with non-exponential tails: Beta mixtures

of exponentials. Stochastic Models, 15, 517-546.

Adamic, L.A. and Huberman, B.A., 2000. The nature of

markets in the World Wide Web. Quarterly Journal of

Electronic Commerce, 1, 5-12.

Akaike, H., 1983. Information measures and model

selection. International Statistical Institute, 44, 277-

291.

Barabasi, A.-L. and Albert, R., 1999. Emergence of

scaling in random networks. Science, 286, 509.

Barabasi, A.-L., 2005. The origin of bursts and heavy tails

in human dynamics. Nature, 435, 207-211.

Bernstein, S.N., 1928. Sur les functions absolument

monotones. ACTA Mathematica, 51, 1-66.

Cover, J., and Thomas, J.A., 1991. Elements of

Information Theory, John Wiley&Sons. New York.

Eckmann, J.-P., Moses, E., Sergi, D., 2004. Entropy of

dialogues creates coherent structures in e-mail traffic.

PNAS, 101, 14333-14337.

Harris, C.M., 1968. The Pareto Distribution As A Queue

Service Discipline. Operations Research, 16, 307-313.

Jaynes, E.T., 1957. Information theory and statistical

mechanics. Physical Review, 106, 620-630.

Johansen, A., 2004. Probing human response times.

Physica A, 338, 286-291.

Krashakov S.A., Teslyuk A.B., and Shchur, LN., 2006 (in

press). On the universality of rank distributions of

website popularity. Computer Networks.

Kryssanov, V.V., Kakusho, K., Kuleshov, E.L., Minoh,

M., 2005. Modeling hypermedia-based

communication. Information Sciences, 174, 37-53.

Kuleshov, E.L., Krysanov, V.V., and Kakusho, K., 2005,

The distribution of term frequency in texts.

Optoelectronics, Instrumentation and Data

Processing, 41, 81-90.

Luce, R.D., 1986. Response Times. Their Role in Inferring

Elementary Mental Organization, Oxford University

Press. New York.

McDonald, J.B. and Xu, J.Y., 1995. A Generalization of

the Beta of the First and Second Kind. Journal of

Econometrics, 66, 133-152.

Mitzenmacher, M., 2003. A Brief History of Generative

Models for Power Law and Lognormal Distributions.

Internet Mathematics, 1, 226–251.

Newman, M.E.J., 2005. Power laws, Pareto distributions

and Zipf's law. Contemporary Physics, 46, 323-351.

Oliveira, J.G. and Barabasi, A.-L., 2005. Darwin and

Einstein correspondence patterns. Nature, 437, 1251.

Sakamoto, Y., Ishiguro, M., and Kitagawa, G., 1986.

Akaike information criterion statistics, KTK

Scientific. Tokyo.

Scalas, E., Kaizoji, T., Kirchler, M., Huber, J., Tedeschi,

A., 2006 (in press). Waiting times between orders and

trades in double-auction markets. Physica A.

Solow, A.R., Costello, Ch.J., Ward, M., 2003. Testing the

Power Law Model for Discrete Size Data. The

American Naturalist, 162, 685-689.

Stouffer, D.B., Malmgren, R.D., and Amaral, L.A.N.,

2005. Comments on “The origin of bursts and heavy

tails in human dynamics”. arXiv:physics/0510216 .

van Zandt, T. and Ratcliff, R., 1995. Statistical mimicking

of reaction time data: Single-process models,

parameter variability, and mixtures. Psychonomic

Bulletin & Review, 2, 20-54.

MODELING THE DYNAMICS OF SOCIAL NETWORKS

249