
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS
Jarrod Trevathan
School of Mathematical and Physical Sciences
James Cook University
Wayne Read
School of Mathematical and Physical Sciences
James Cook University
Keywords:
Continuous double auctions, online auctions, share trading, competitive analysis.
Abstract:
Market clearing is the process of matching buy and sell bids in securities markets. The allocative efficiency
of such algorithms is important, as the Auctioneer is typically paid a commission on the number of bids
matched and the volume of quantity traded. Previous algorithms have concentrated on price issues. This paper
presents several market clearing algorithms that focus solely on allocating quantity among matching buy and
sell bids. The goal is to maximise the number of bids matched, while at the same time minimise the amount
of unmatched quantity. The algorithms attempt to avoid situations resulting in unmarketable quantities (i.e.,
quantities too small to sell). Algorithmic performance is tested using simulated data designed to emulate the
Australian Stock Exchange (ASX) and other world stock markets. Our results show that it is difficult to avoid
partial matchings as the complexity of doing so is NP-complete. The optimal offline algorithm for partial
quantity matching is used as a benchmark to compare online matching strategies. We present three algorithms
that outperform the ASX’s strategy by increasing the number of bids matched, the amount of quantity matched,
and the number of bids fully matched.
1 INTRODUCTION
Securities markets such as the New York Stock Ex-
change
1
and the Australian Stock Exchange
2
(ASX),
employ a form of auction referred to as a Continuous
Double Auction (CDA). A CDA has many buyers and
sellers continuously trading a commodity. Buy and
sell bids accumulate over time and must be cleared.
The method by which buy and sell bids are matched
is referred to as a market clearing algorithm. In gen-
eral, two bids can only be matched if: 1) both bids
are currently active (i.e., they haven’t expired or pre-
viously been cleared); and 2) the price of a buy bid
equals or exceeds the price of a sell offer.
The efficiency and performance of a clearing al-
gorithm is important. An algorithm must be able to
cope with large numbers of bids, and make timely de-
cisions which maximise the benefits for buyers and
sellers. Furthermore, the Auctioneer/Broker typically
gains commission on the number of bids cleared, and
the volume of quantity traded. As a result, the algo-
rithm must also strive to maximise both of these fac-
1
http://www.nyse.com
2
http://www.asx.com.au
tors.
Stock exchanges have been fully automated since
the early 1990s (see (Economides and Schwartz,
1995)). The ASX uses a computerised clearing sys-
tem referred to as the Stock Exchange Automated
Trading System (SEATS). SEATS imposes a strict
time-based priority on matching bids. Bids are or-
dered according to price, and are then matched based
on their arrival times. Larger bids are not given prior-
ity over small bids.
Alternate strategies for market clearing have been
discussed by (Wellman and Wurman, 1999; Sand-
holm and Suri, 2001). (Sandholm et al., 2002) show
that in some situations, the Auctioneer can increase
the profit from a sale (i.e., the price difference be-
tween a buy and sell bid). This is achieved by not
matching bids immediately, but rather waiting for a
better match to possibly eventuate. (Sandholm et al.,
2002) also describe how profit producing matches can
subsidise loss producing matches to increase the total
number of bids matched.
The market clearing model used by (Sandholm et
al., 2002) mainly attempts to maximise the amount of
surplus generated by the matching process. In doing
so, the model only considers price, and assumes that
126
Trevathan J. and Read W. (2006).
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS.
In Proceedings of the International Conference on e-Business, pages 126-133
DOI: 10.5220/0001426901260133
Copyright
c
SciTePress

the quantity of each bid is one unit. If a bidder desires
to bid for more than one unit, then they must enter a
number of bids equal to the amount of the quantity.
(e.g., five separate bids are required to bid for a quan-
tity of five units.)
This approach is not very practical when the
amount of quantity transacted is large. For example,
in the case where a bidder desires 10, 000 units, it is
unlikely they would be willing to expend time and ef-
fort to submit 10, 000 bids. While software bidding
agents and other automated methods could be used
to alleviate this situation, there are further issues re-
garding allocating quantity among bids. For example,
a bidder may desire n units, but the market is only
able to clear ρ units, where ρ < n. This may leave
the bidder with an unmarketable quantity. An unmar-
ketable quantity, is a quantity that is too small to sell,
after taking into account Auctioneer commission, and
other associated costs.
In this paper, we propose the idea of a variable
quantity market clearing algorithm. Once bids have
been ordered according to price, a variable quantity
market clearing algorithm is used to efficiently allo-
cate quantity among matching buy and sell bids. The
algorithm attempts to match up as many bids as possi-
ble, with as little or no unmatched quantity outstand-
ing. The primary goal is to avoid situations that result
in unmarketable quantities.
This paper presents several variable quantity mar-
ket clearing algorithms. The first algorithm shows
why it is difficult in practice to avoid unmarketable
quantities. The second algorithm gives the optimal of-
fline solution in terms of avoiding unmarketable quan-
tities. The third algorithm is online, and is the ap-
proach used by SEATS. The remaining algorithms are
online, and try to outperform Algorithm 3, using dif-
fering strategies including; waiting until a bid is ready
to expire before matching, subsidising short falls in
allocation, and giving priority to bids with smaller
quantities.
The algorithms have been tested on simulated data
designed to emulate the workings of the ASX. Each
algorithm is assessed according to the number of
bids matched, the volume of quantity traded and how
much unmarketable quantity is produced. We show
that it is possible to out-perform SEATS in terms of
these goals.
This paper is organised as follows: The CDA
model and goals of the algorithms are discussed in
Section 2. Section 3 presents several market clear-
ing algorithms for matching variable quantities of an
item. A comparison of the algorithms is given in
Section 4, and Section 5 provides some concluding
remarks.
2 PRELIMINARIES
This section presents a CDA model for describing
variable quantity market clearing algorithms. The
goals for a clearing algorithm are discussed, and basic
statistics are introduced for measuring how an algo-
rithm performs in terms of these goals.
2.1 Model
The algorithms presented in this paper are based on a
temporal clearing model. This consists of a set of buy
bids, B, and a set of sell bids, S. Each bid v ∈ B ∪ S
has the components (type, t
i
, t
j
, p, q).
type = {buy, sell} denotes the type of the bid. It
is common in securities markets to refer to a buy bid
as a bid and a sell bid as an offer.
A bid, v, is introduced at time t
i
(v), and removed
at time t
j
(v), where t
i
(v) < t
j
(v). A bid, v, is said to
be alive in the interval [t
i
(v), t
j
(v)]. To be a candidate
for a particular matching, two bids must have a period
where their arrival and expiration times overlap. Two
bids v, v
′
∈ B ∪ S are said to be concurrent, if there
is some time when both are alive simultaneously.
p denotes the price of a bid. In order to run the
clearing algorithm, bids are first ordered according
to price. The definition of concurrency now extends
to two bids that met the criteria for matching based
on price. This allows us to concentrate on match-
ing quantities rather than prices. The problem now
becomes the opposite extreme of the price-matching
problem from (Sandholm et al., 2002).
q ∈ [q
min
, q
max
] denotes the quantity, and q(v) is
the quantity desired by bid v. q must be greater than
zero and an integer, i.e., it is not possible to buy or sell
a fraction of a quantity.
The temporal bidding model is abstracted as an
incomplete interval graph. An incomplete interval
graph is a graph G = (V, E), together with two func-
tions t
i
and t
f
from V to [0, ∞] such that:
1. For all v ∈ V , t
i
(v) < t
f
(v). (i.e., the entry time
is less than the exit time.)
2. If (v, v
′
) ∈ E, then t
i
(v) ≤ t
f
(v
′
) and t
i
(v
′
) ≤
t
f
(v). (i.e., bids are concurrent.)
An incomplete interval graph can be thought of as an
abstraction of the temporal bidding problem. The fact
that bids come in two types (buy and sell) and have
prices attached to them is ignored. Instead a black
box “E” is used, that given two bids v, v
′
, outputs
whether or not they can be matched. This generalisa-
tion provides a simple framework for describing and
developing clearing algorithms.
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS
127

2.2 Goals
The quantity matching algorithms presented in this
paper have the following goals:
Maximise Number of Matches
The first goal is to maximise the number of matches
between buy and sell bids. This is important as the
Auctioneer typically gains a commission based on the
number of bids matched.
The Bid Match Ratio (BMR) is used to measure
the number of bids matched, α, in relation to the total
number of bids, n. This is calculated as:
BM R = α/n × 100
where 0 ≤ BMR ≤ 100.
Maximise Volume of Quantity Matched
The second goal is to maximise the amount of quan-
tity matched. The Auctioneer also typically gains a
commission proportional to the volume of quantity
cleared.
The Quantity Match Ratio (QMR) is used to mea-
sure the amount of matched quantity, δ, in relation to
the total quantity, γ. This is calculated as:
QMR = δ/γ × 100
where 0 ≤ QMR ≤ 100.
Maximise Full Quantity Matches
A full match occurs when a bid has had its entire
quantity matched and cleared. A partial match occurs
when a bid which is in the process of being matched,
expires with an outstanding quantity that hasn’t been
filled. The Auctioneer must strive to satisfy the entire
quantity of a bid, so that a bidder is not left with an
unmarketable quantity.
The Full Match Ratio (FMR) examines the bids
that were fully matched, ǫ, against the total number
of matches, ζ. This is calculated as:
F MR = ǫ/ζ × 100
where 0 ≤ FMR ≤ 100.
2.3 Analysing Efficiency
Within both Computer Science and Finance, many
problems reduce to trying to predict the future. For
example, cache/virtual memory management, process
scheduling, or predicting future returns for an asset.
Such problems become trivial if the future is known
(i.e., the stream of future memory requests or tomor-
row’s newspaper), but typically we only have access
to the past.
An offline problem provides access to all the rele-
vant information to compute a result. An online prob-
lem continually produces new input and requires an-
swers in response. Offline problems have the benefit
of perfect knowledge, anas such they generally out-
perform online problems (if designed properly).
An offline clearing algorithm learns of all bids up
front. That is, all bids must be submitted before a
closing time. The algorithm is then able to match
bids at its discretion. An online clearing algorithm
only learns about bids as they are introduced over
time. The online algorithm has the added complex-
ity of bids expiring before they can be matched.
Securities markets employ both types of algo-
rithms. For example, the online algorithm is used
during trading hours and the offline algorithm is used
after hours while bids accumulate over night.
Competitive analysis allows an online algorithm to
be compared based on its ability to successfully pre-
dict the future. The efficiency of an online solution is
compared to the optimal offline solution. The closer
an online algorithm performs to the optimal offline al-
gorithm, the more ‘competitive’ the algorithm is.
An algorithm, A, is said to be c-competitive if there
exists some constant b, such that for every sequence
of inputs σ:
cost
A
(σ) ≤ c cost
OP T
(σ) + b
where OPT is the optimal offline algorithm. In de-
veloping an online algorithm, the goal is to attain a
competitive ratio, c, as close to one as possible. The
worse the performance of an algorithm, the larger c
is.
In this paper, an optimal offline solution is pre-
sented for clearing variable quantities. Several on-
line strategies are discussed, and their performance is
compared based on their competitive ratios. Related
literature on how competitive analysis has been ap-
plied to online auctioning can be found in (El-Yaniv et
al., 1992; Lavi and Nisan, 2000; Bagchi et al., 2001).
3 QUANTITY CLEARING
ALGORITHMS
This section presents several market clearing algo-
rithms for matching variable quantities of an item.
3.1 Algorithm 1
The initial goal for this algorithm is to either match
quantities entirely, or not at all (i.e., bids are indivisi-
ble). This effectively eliminates the possibility of un-
marketable quantities.
For example, a buy and sell bid each for 1 unit, can
be matched. In addition, a buy bid for 2 units can
be matched to two sell bids that are for 1 unit each.
However, if a buyer is demanding 2 units, and there is
a seller supplying only 1 unit, then neither of the bids
can be matched.
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
128

Matching indivisible quantities is similar to the
Knapsack problem. Consider the case where there is
a buy bid v for a quantity q(v) = n. In order to match
this bid, the algorithm is required to select either a sin-
gle sell bid v
′
offering n units, or some combination
of n or less sell bids, where the collective quantity on
offer sums exactly to n. The complexity of the algo-
rithm for matching indivisible quantities is dominated
by this step.
The problem of trying to find a subset of inte-
gers from a given set, that sums to a particular value,
is referred to as the subset sum problem. The sub-
set sum problem is considered to be hard, and there
are no known algorithms to efficiently solve it. The
quandary of matching indivisible quantities can be re-
duced to the subset sum problem. The subset sum
problem is NP-complete, and therefore the indivisible
quantity matching problem is also NP-complete. As a
result, it is not feasible to construct an efficient algo-
rithm that does not deliver unmarketable quantities.
Even if this algorithm were practical, it does not
necessarily perform well in terms of the number of
bids matched, as it is too restrictive. The costs of
unmarketable quantities must be weighed against the
benefits of relaxing the indivisibility constraint. Do-
ing so allows the clearing process to benefit the major-
ity of bidders, while at times delivering an undesirable
result to a minority. The problem now becomes how
to limit the extent of unmarketable quantities.
3.2 Algorithm 2
This algorithm is offline and allows bids to be divis-
ible. A particular bid is matched with as many other
candidate bids as required to satisfy it. If there is
not enough available quantity, the bid is considered
as partially matched. A partial matching can result
in bidders holding unmarketable quantities. The goal
of this algorithm is to match as many bids as possible
and minimise partial matchings.
A greedy strategy is employed which successively
subtracts the smaller bid quantity from the larger op-
posite bid quantity. The algorithm keeps track of
the current unmatched buy and sell quantities at each
stage of the algorithm using two variables, α
b
and
α
s
. Once a particular bid has been allocated its ex-
act quantity, it is cleared (i.e., moved to the set M).
The algorithm is as follows:
1. α
b
= α
s
= 0.
2. While there are more vertices in G
(a) if α
b
and α
s
= 0 then
i. get next v and v
′
from G
ii. if q(v) > q(v
′
) then
α
b
= q(v)
iii. else
α
s
= q(v
′
)
(b) else if α
b
> 0 then
i. get next v
′
from G
ii. if α
b
> q(v
′
) then
A. α
b
= α
b
− q(v
′
)
B. place edge between v and v
′
, move v
′
to M
iii. else
A. α
s
= q(v
′
) − α
b
B. place edge between v and v
′
, move v to M
(c) else if α
s
> 0 then
i. get next v from G
ii. if α
s
> q(v) then
A. α
s
= α
s
− q(v)
B. place edge between v and v
′
, move v to M
iii. else
A. α
b
= q(v) − α
s
B. place edge between v and v
′
, move v
′
to M
As all bids are concurrent, the proposed solution is
equivalent to summing the volumes of buy and sell
bids, and subtracting the smaller from the larger. This
algorithm is the optimal solution for matching vari-
able quantities, and is the basis for the operation of
the forthcoming online algorithms.
3.3 Algorithm 3
This algorithm is online and uses the same strategy as
Algorithm 2. Bids have entry and expiration times.
When a bid is introduced, it is matched with as many
other bids as possible. However, when expiration time
is reached, the bid is cleared regardless of whether
it has been fully matched. That is, if a bid is in the
process of being matched when it expires, its out-
standing quantity remains unfilled.
This is the actual approach used by SEATS and
most of the world’s securities markets. It is simple,
fair and performs relatively well. However, this algo-
rithm performs significantly worse than the previous
algorithm, and can result in many bids expiring par-
tially matched.
3.4 Algorithm 4
Algorithm 4 aspires to out-perform the previous algo-
rithm. When a bid expires in Algorithm 3, there may
be a significant amount of residual unmatched quan-
tity. In addition, bids that arrive later, but expire ear-
lier have to wait on earlier bids, with later expiration
times. Algorithm 4 modifies the previous algorithm
by waiting till a bid is about to expire, before match-
ing it with as many other bids as possible based on
expiry time.
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS
129

3.5 Algorithm 5
Algorithm 5 uses an inventory of quantity to offset the
unfilled portions of partially matched bids. We refer
to this as subsidising.
To acquire an inventory, the Auctioneer must first
collect surplus quantity. A surplus occurs when the
quantity on offer is greater than the quantity being
bid for. If a buy bid demands a quantity less than
the quantity offered by a sell bid, then the Auctioneer
pays for the surplus. The surplus quantity is placed
in an inventory that can be used at a later date to
subsidise shortfalls in allocation. A shortage occurs
when there is less quantity on offer than the amount
bid for.
Determining the extent to subsidise shortages re-
quires choosing a threshold, which is the maximum
amount that can be subsidised. This is denoted by θ.
The algorithm proceeds in a similar manner to the
previous online algorithms. However, when a bid is
about to expire, it becomes a candidate for subsidis-
ation. Let I denote the current inventory of quantity
held by the algorithm. The subsidisation process is as
follows:
1. if v is type sell then
(a) if (I + q(v) < θ) then
I = I + q(v)
(b) else
temp = θ − I
I = I + temp
q(v) = q(v) − temp
2. else if v is type buy then
(a) if (I < q(v)) then
q(v) = q(v) − I
(b) else
I = I − q(v)
q(v) = 0
3. Move v to M
The choice of θ depends on the risk the Auctioneer
is willing to take. If θ is set too small, the Auctioneer
will not be able to significantly influence the clearing
process. However, if θ is set too large, the Auctioneer
might be left holding a large quantity at the close of
trade, which is undesirable.
The Remaining Inventory Ratio (RIR) is used to
measure the extent of remaining quantity held by the
Auctioneer at the close of trade. The RIR is calculated
as follows:
RIR = I/θ × 100
where 0 ≤ RIR ≤ 100.
3.6 Algorithm 6
A problem with the greedy approach of Algorithms 2
and 3 is that a large number of smaller bids may be
waiting on a earlier, larger bid to clear.
In economic systems it is usually the case that a
smaller number of individuals own the most. Like-
wise, in share trading there tend to be more bids for
smaller quantities compared to larger bids. Large bids
are often due to financial institutions such as super-
annuation schemes or managed funds that pool the
capital of many smaller investors. An Auctioneer can
take advantage of the above situation by clearing the
smaller bids first. This will increase the number of
bids matched while leaving the volume traded un-
changed.
Algorithm 6 gives priority to smaller bids. That
is, if a large bid is in the process of being matched,
it is ‘pre-empted’ when a smaller bid arrives. This is
analogous to the problem of process scheduling where
many processes compete for CPU time. In shortest
job first scheduling, the process with the shortest time
is given priority to use the CPU.
In terms of market clearing, quantity represents
CPU time and bidders are the processes. However,
matching bids is two sided and therefore more com-
plicated than process scheduling. That is, the set of
buy bids represents a set of processes, and the set of
sell bids represents another set of processes. When a
large buy bid is matched to several smaller sell bids,
the buy bid is equivalent to the CPU for that instance
in time (and vice versa).
4 COMPARISON
This section provides a comparison of the market
clearing algorithms. Each algorithm is assessed
on its ability to achieve the goals outlined in Sec-
tion 2.2. These goals are: maximise the number
of matched bids (BMR), maximise the volume of
quantity matched (QMR), and maximise the num-
ber of fully matched bids (i.e., avoid partial match-
ings)(FMR).
The Research Auction Server at James Cook Uni-
versity, is an online auction server used to conduct
research into online auctioning [see (Trevathan and
Read, 2006)]. The auction server contains a simu-
lation environment for testing computational aspects
related to auctioning online. This includes emulating
the workings of the ASX by generating the kind of
bidding data that exists in share markets. The clearing
algorithms were tested in this setting using the simu-
lated data.
The input parameters for a test are the number of
bids, n, the maximum quantity allowable for a bid,
q
max
, and the total time, t. Time is split into discrete
units representing seconds. Entry and Exit times are
randomly generated between time period one and t.
Bids are randomly allocated quantities between one
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
130
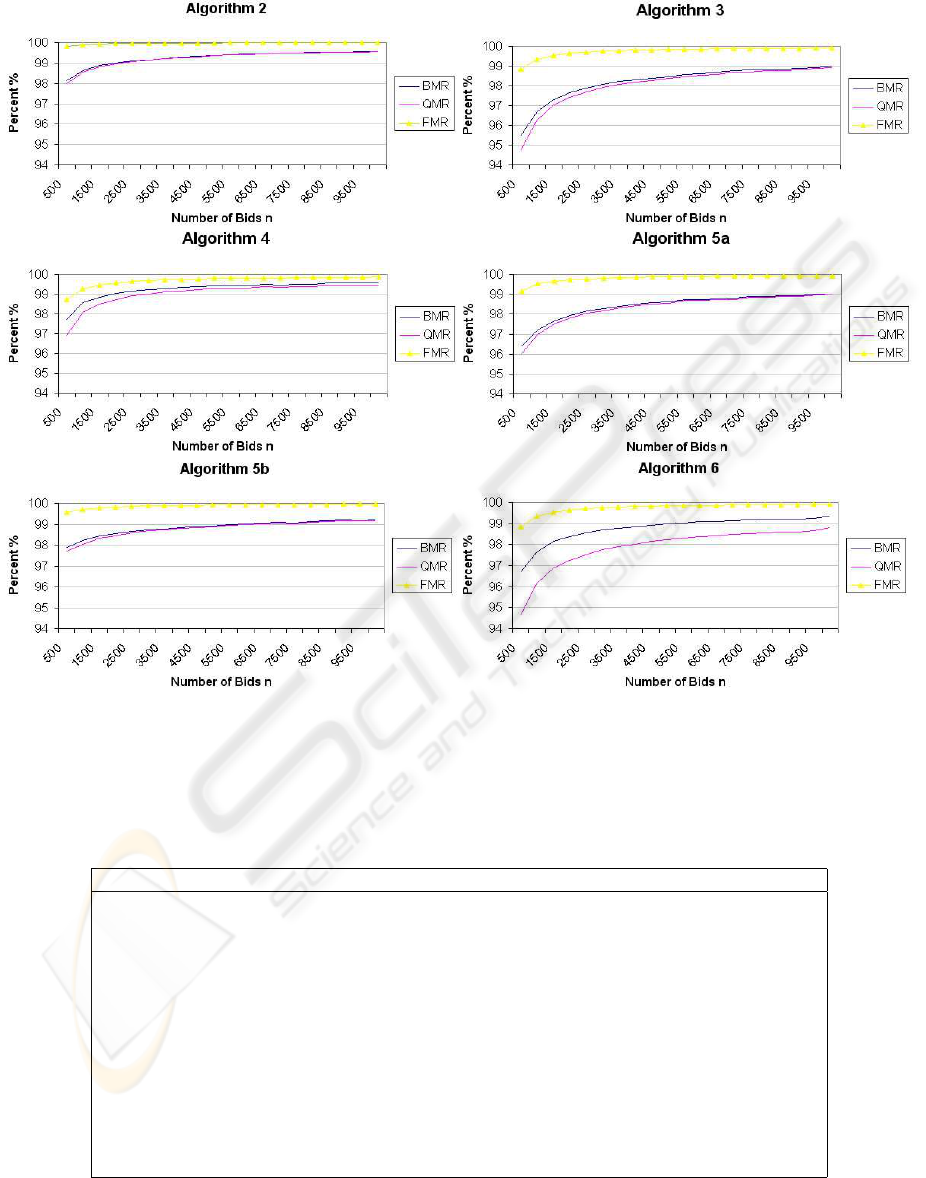
Figure 1: Algorithmic Performance on Simulated Data.
Table 1: Comparison of Variable Quantity Market Clearing Algorithms.
Type BMR QMR FMR RIR Competitive Ratio
Alg. 2 offline 0.43 ln(n) 0.47 ln(n) 0.05 ln(n) - Optimal
Alg. 3 online 1.05 ln(n) 1.23 ln(n) 0.29 ln(n) - 2.44
Alg. 4 online 0.51 ln(n) 0.71 ln(n) 0.30 ln(n) - 1.18
Alg. 5a online 0.81 ln(n) 0.91 ln(n) 0.21 ln(n) 50.61% 1.88
Alg. 5b online 0.43 ln(n) 0.48 ln(n) 0.11 ln(n) 50.13% 1.00
Alg. 6 online 0.77 ln(n) 1.20 ln(n) 0.29 ln(n) - 1.79
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS
131

and q
max
. For now, it is assumed that entry/exit times
and quantities are uniformly distributed among bid-
ders, and there is an even number of buy and sell bids
(i.e., # buy = # sell = n/2).
Figure 1 shows the individual results for each al-
gorithm (except Algorithm 1). Each algorithm was
tested using varying numbers of bids up to a maxi-
mum of n = 10, 000, with q
max
= 1000. The online
algorithms are shown for a six-hour time period (i.e.,
t = 21, 600 seconds). This is consistent with the trad-
ing hours of the ASX and most share markets.
In general, all algorithms run in a time proportional
to n. Furthermore, the larger the value of n, the bet-
ter the performance. Additionally, online algorithms
tended to perform better with smaller values of t. The
size of q
max
does not significantly affect the running
time or the performance of the algorithms.
For each algorithm, trendlines are calculated using
the method of least squares. The resulting equations
for each algorithm are listed in Table 1. The smaller
the value of the coefficient of ln(n) for the BMR,
QMR and FMR, the better the performance. Com-
petitive analysis is used to compare the performance
of the online algorithms to the optimal offline algo-
rithm. The BMR is used to determine an algorithm’s
competitive ratio.
Algorithm 2 is the optimal offline strategy for
matching divisible bids. Only a small percentage of
bids were partially matched. This algorithm is the
benchmark to which all online algorithms are com-
pared. This algorithm is 1 − competitive.
Algorithm 3 is online, and orders bids strictly ac-
cording to entry time (the approach used by SEATS).
This algorithm performs significantly worse than
the offline algorithm. This algorithm is 2.44 −
competitive.
Algorithm 4 waits until a bid is about to expire be-
fore matching it. This strategy is a significant im-
provement on Algorithm 3. The reason for this is that
by waiting, the algorithm is essentially acting simi-
lar to the offline algorithm. Although this algorithm
doesn’t have perfect knowledge about future bids, de-
laying matching allows the algorithm to gather more
information, which it can use to optimise its match-
ing decision. However, Algorithm 4’s FMR does not
fare much better than Algorithm 3. This algorithm is
1.18 − competitive.
Algorithm 5 uses an inventory of quantity to sub-
sidise deficit quantity trades. Two tests were con-
ducted with differing values of θ. The first test (re-
ferred to as Algorithm 5a), examined the effect of
minimal subsidisation. The second test (referred to
as Algorithm 5b), used excessive subsidisation. Both
tests were also assessed on the amount of inventory
remaining at the end (i.e., the RIR, see Section 3.4).
Algorithm 5a uses minimal subsidisation where
θ = 1000. This algorithm improved upon Algo-
rithm 3 (i.e., SEATS) with regard to its BMR and
QMR. This algorithm achieved a better FMR than
both previous online algorithms. This algorithm is
1.88 − competitive.
Algorithm 5b uses excessive subsidisation where
θ = 5000 (5 × q
max
). This algorithm’s perfor-
mance approaches Algorithm 2 in terms of BMR and
QMR. It also attains an excellent FMR. This algo-
rithm is 1 − competitive. If subsidisation were with-
out bound, eventually all bids would be matched.
The amount of remaining inventory (i.e., RIR) for
Algorithm 5a and 5b were 50.61% and 50.13% re-
spectively. This shows that over time, the clearing
algorithm will always be holding an inventory that
is half full (i.e., θ/2). While excessive subsidisa-
tion may achieve significant results, the practicality
of subsidising must be weighed against the level of
risk the Auctioneer is willing to take.
Algorithm 6 prioritises bids with smaller amounts
of quantity. This algorithm out performs Algorithm
3 (SEATS) in terms of its BMR, and improves on us-
ing minimal subsidisation. The QMR and FMR are
marginal improvements on Algorithm 3. This algo-
rithm is 1.79 − competitive. This result is consistent
with the goals of the algorithm. That is, we strived for
an increase in the BMR by matching a larger number
of smaller bids. In doing so, the amount of matched
quantity would be roughly the same.
5 CONCLUSIONS
A market clearing algorithm’s performance greatly
affects the revenue earned by the Auctioneer, and the
welfare of the bidders. Previous literature on market
clearing only addresses price issues, and neglects con-
cerns regarding allocative efficiency.
This paper presents several market clearing algo-
rithms that focus solely on allocating quantity among
matching buy and sell bids. The algorithms attempt
to avoid situations resulting in unmarketable quanti-
ties (i.e., quantities too small to sell).
We show that it is difficult to avoid partial match-
ings, as the complexity of doing so is NP-complete.
The problem of matching bids with indivisible quan-
tities reduces to the subset sum problem. The sub-
set sum problem is a renowned NP-complete prob-
lem. As a result, an efficient algorithm cannot be con-
structed to avoid partial matchings.
An optimal offline algorithm is presented for
matching bids with divisible quantities. The algo-
rithm employs a greedy strategy. Each bid is matched
with as many other bids as required to satisfy it. This
approach achieves a high match rate. However, the
algorithm can result in a limited number of bidders
receiving partial matchings.
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
132

SEATS and most of the world’s stock exchanges
use an online version of the previous algorithm. Bids
are strictly ordered by price and time. Larger bids are
not given priority over smaller bids. This algorithm
is simple and fair. However, it performs significantly
worse than the optimal offline solution.
We propose several alternate methods for clearing
variable quantities. The goal is to out-perform the ap-
proach used by SEATS. Algorithmic performance is
tested using simulated data designed to emulate the
ASX. Competitive analysis is used to compare the
performance of an online algorithm to the optimal of-
fline solution.
The first of our proposed algorithms showed that
there is some benefit in waiting rather than matching
with the first available quantity. Waiting until a bid
is about to expire before matching, makes the algo-
rithm function more like its offline counterpart. This
algorithm performs significantly better than SEATS.
The next algorithm collects surplus quantity to sub-
sidise shortfalls in allocation. With minimal subsidi-
sation, this algorithm can deliver less partial match-
ings than SEATS. With excessive subsidisation, this
algorithm can approach the efficiency of the optimal
offline solution. However, the level of subsidisation
must be weighed against the potential to be left hold-
ing a large inventory at the end of matching.
Alternately, the final algorithm gives priority to
bids with smaller quantities. If a bid is in the process
of being matched, it is pre-empted by a bid with a
smaller quantity. This approach strongly outperforms
SEATS in terms of the number of bids matched. How-
ever, it only offers a minor improvement in delivering
less partial matchings.
In a rigid environment such as a share market,
these mechanisms may not be deemed as initially fair.
However, our results show that over time, the pro-
posed algorithms can attain a better outcome than
SEATS.
The tests assume there are an even number of buy
and sell bids with a uniform distribution of quantity.
In reality this would not occur. Increasing the number
of either type essentially increases the volume on of-
fer for one type in relation to the other. This degrades
performance regardless of the algorithm employed. In
the extreme case there will be all of one type and none
of the other, which in this case the BMR and QMR
would be zero. Having an even number of each type
of bid is a neutral point. Skewing the number of bids
one way or the other is detrimental to performance.
Bids are uniformly distributed across time. In re-
ality, there may be periods of high bidding volume
and also low volume periods. Future work involves
using a Poisson probability distribution to model the
frequency of the bids. This should help show how the
algorithms perform on bursty data.
It would be intuitive to test the algorithms on real
stock market data. However, we have found such data
difficult to obtain. There exist many commercial se-
curities market data providers such as Bourse Data
3
who sell real-time and historical market data. How-
ever, the market depth provided only lists the aggre-
gate quantity at a price level and not the individual
bids.
REFERENCES
Bagchi, A., Chaudhary, A., Garg, R., Goodrich, M. and Ku-
mar, V. (2001). Seller-focused Algorithms for Online
Auctioning, in Proceedings of WADS 2001, 135-147.
Economides, N. and Schwartz, R. (1995). Electronic Call
Market Trading, Journal of Portfolio Management,
vol. 21, no. 3, 10-18.
Kao, M. and Tate, S. (1999). Online Difference Maximisa-
tion, SIAM Journal of Discrete Mathematics, vol. 12,
no. 1, 78-90.
El-Yaniv, R., Fiat, A., Karp, R. and Turpin, G. (1992). Com-
petitive Analysis of Financial Games, in Proceedings
of the 33rd Symposium on Foundations in Computer
Science, 327-333.
Lavi, R. and Nisan, N. (2000). Competitive Analysis of In-
centive Compatible Online Auctions, in Proceedings
of the 2nd ACM Conference on Electronic Commerce,
233-241.
Sandholm, T. and Suri, S. (2001). Market Clearability, in
Proceedings of the Seventeenth International Joint
Conference on Artificial Intelligence (IJCAI), 1145-
1151.
Sandholm, T., Blum, A. and Zinkevich, M. (2002). On-
line Algorithms for Market Clearing, in Proceedings
of the 13th SIAM Symposium on Discrete Algorithms
(SODA), 971-980.
Trevathan, J. and Read, W. (2006). RAS: a system for sup-
porting research in online auctions, ACM Crossroads,
ed. 12.4, 23-30.
Wellman, M. and Wurman, P. (1999). A Parameterization of
the Auction Design Space, in Proceedings of the Sec-
ond International Conference on Autonomous Agents
(AGENTS), 301-308.
3
http://www.boursedata.com.au
VARIABLE QUANTITY MARKET CLEARING ALGORITHMS
133
