WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED

FAIR QUEUING (WFQ) SCHEDULER

Gianmarco Panza, Valentin Besoiu

CEFRIEL Network Systems Unit, Milan, Italy

Catherine Lamy-Bergot

THALES Communications, Colombes, France

Filippo Sidoti, Roberto Bertoldi

WIND Telecomunicazioni S.p.A., Rome, Italy

Keywords: DiffServ, proportional services, QoS, weight updating, WFQ.

Abstract: This work aims to analyze different weight updating methods for a dynamic Weighted Fair Queuing (WFQ)

scheduler providing Quality of Service (QoS) guarantees for the applications of the IST PHOENIX project

and for new value-added services in general. Two weight updating methods are investigated in terms of

granted delays to concerned service classes and buffer utilization of the related queues at a given IP

interface. In particular, a novel weight updating based on the Knightly’s theory is proposed. Simulation

results have demonstrated that a dynamic WFQ based on either of the weight updating methods can well

support a proportional relative model of QoS in a Diff-Serv architecture in an IP-based Next Generation

Network. The designed system is extremely simple and effective, and with low computational overhead by

employing an innovative technique to evaluate the trend of the entering traffic aggregates, in order to trigger

a scheduler’s weights updating only when needed.

1 INTRODUCTION

The PHOENIX IST project main goal is to

effectively exploit the available bandwidth on

wireless links (WLAN, UMTS, 4G…) that is

dynamic by nature, providing optimised solutions

for multimedia transmission over IP-based wireless

networks. To reach this goal, a scheme was

developed (PHOENIX) offering the possibility to let

the application world (source coding, ciphering) and

the transmission world (channel coding, modulation)

talk together over an IP protocol stack, so that they

can jointly develop an end-to-end optimised wireless

communication (termed as JSCC/D compliant

system).

However, adequate Quality of Service (QoS)

guarantees must be provided along the

communication path through-out the network, both

for the user data and the control/signalling

information to be exchanged.

Advances in computing and network

technologies have made it possible to support QoS

guarantees in packet switching network. There are

two approaches: the Integrated Service (IntServ)

(Wroclawski, 1997) and Differentiated Service

(DiffServ) (Nichols, 1998)(Blake, 1998). IntServ

tried to ensure end-to-end and per flow QoS of data

traffics. However, it is quite difficult to implement

on a large scale, such as in the Internet. For this

reason, DiffServ, which only provides a limited

number of service classes, was then proposed. It

aggregates the flows with the same QoS

requirements, and serves the packets according to

predefined traffic contracts. Instead of achieving

per-flow QoS, DiffServ provides guarantees at an

aggregate level.

Relative and absolute service differentiation are

two categories of the DiffServ model. Relative

DiffServ ensures the ratios of the quality level

between classes, while absolute DiffServ absolute

service guarantees. Obviously, the first is more

Panza G., Besoiu V., Lamy-Bergot C., Sidoti F. and Bertoldi R. (2006).

WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED FAIR QUEUING (WFQ) SCHEDULER.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 42-49

DOI: 10.5220/0001567400420049

 SciTePress

straightforward to deploy as well as effective with

proper resource provisioning in the network. There

is a variant in this category, called proportional

service differentiation (Li, 2000).

Weighted Fair Queuing (WFQ) (Keshav, 1997)

is a scheduling discipline nowadays widely applied

to QoS-enabled routers. In WFQ, single flows or

traffic classes are served on the basis of the weight

assigned to the related queue. The weight can be

dynamically determined (Panza, 2005)(Li,

2000)(Kun, 2000) according to the mutual ratio

between QoS factors assigned to each queue in order

to achieve QoS guarantees, such as delay and loss, in

a proportional manner.

In this paper, two different methods for the

weight updating of a dynamic version of the WFQ

scheduler are analyzed and compared with respect to

the goal of effectively supporting a proportional

relative QoS model in a DiffServ architecture. As a

new proposal, the latter method is based on the

sophisticated Knightly’s theory (Knightly, 1998).

Moreover, the novel idea of applying a statistical

test allows to save computational power by

triggering a weight updating when needed only.

The remainder of this paper is organized as

follows. Next section briefly explains the main

achievements in the field, concerning dynamic

versions of WFQ, as well as Knightly’s theory, the

basis for the novel weight updating method. Then, a

description of the work is carried out, the most

relevant simulation results and analyses are

presented.

Finally, last section summarizes the main

achievements and conclusions.

2 WEIGHTED FAIR QUEUEING

DISCIPLINE AND KNIGHTLY’S

THEORY

2.1 Dynamic WFQ

A Dynamic WFQ (Panza, 2005)(Li, 2000)(Kun,

2000) is able to dynamically and consistently adapt

the queue weights according to the time-variant

amount of the incoming traffic and the pre-assigned

target QoS.

The fundamental issue is to correlate the

burstiness of the traffic with the weight value in

order to achieve given delay and loss guarantees.

The measurement of the burstiness of the

aggregate entering each queue could be realized by

evaluating the resulting buffer dimension (Panza,

2005)(Li, 2000), which is ultimately related to the

worst-case delay experienced by packets in the

queue.

For what concerns the QoS, we aim to support a

proportional relative model. Each queue is assigned

a static factor so that the guarantees provided to the

set of queues should be in line with the mutual ratio

of the said factors. For example, if the queue Qi and

Qj have the factors Pi and Pj respectively, with

Pj=2Pi, the QoS provided to Qj should be two times

better then the one granted to Qi. Hence, no absolute

QoS assurances are supported in this case.

As proposed in (Panza, 2005)(Li, 2000), where

also preliminary results are reported, if in a given

interval Tn, Bn represents the average buffer filling

of Qn, which is associated with the factors Pn, the

queue weights could be determined by the resolution

of a linear system whose equations are of the form:

(Bi/Bj)(Pi/Pj) = (Wi/Wj)

where, Wi and Wj are the weights to be assigned to

the queues Qi and Qj, respectively.

2.2 Knightly’s Theory

Knightly’s theory (Knightly, 1998) is based on a

parametric characterization of the traffic, referring to

an analytical representation, in terms of a temporal

function, of the cumulative arrivals process for the

concerned traffic. This can be described by a

specific traffic constraint function, i.e. a function of

temporal variables that represents an upper-bound

envelope. It is a model for the arrival traffic derived

from the classic leaky bucket characterization of the

arriving cumulative traffic, a monotonically

increasing piece-wise function b(t) of different

slopes. For each slope added to the model, two

further parameters are to be introduced (i.e.

intersection σ and angular coefficient ρ). For

example, a dual leaky bucket model has the

following analytical expression

b(t)=min{σ1+ ρ1 t, σ2+ ρ2 t} (1)

WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED FAIR QUEUING (WFQ) SCHEDULER

bits

(

)

(

)

MTU

bits

(

)

(

)

(

)

(

)

(

)

(

)

MTU

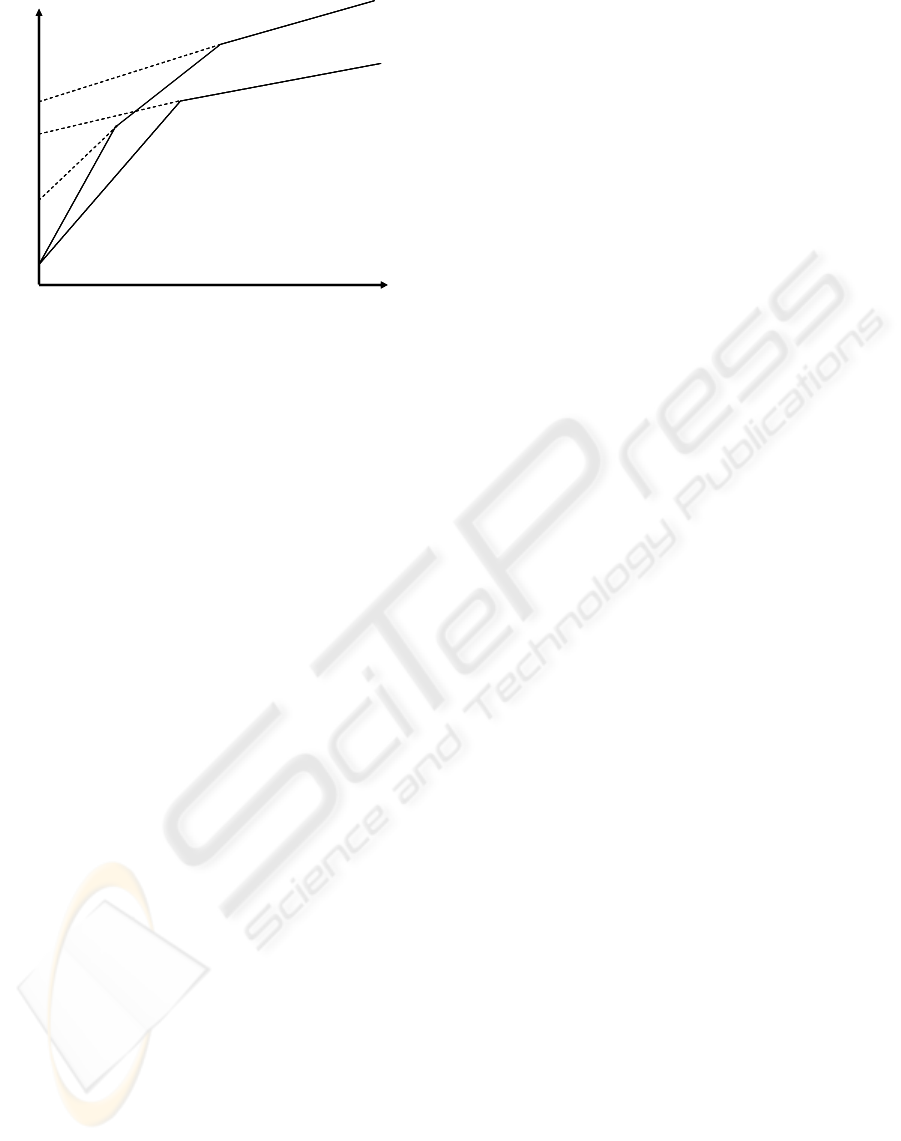
Figure 1: Examples of traffic constraint function of dual

and triple leaky bucket type (MTU = Maximum Transfer

Unit).

In the case of audio and video traffic flows, as

demonstrated by experimental analysis (Knightly,

1997), this function can be simply constituted by

two or three slopes (see the figure above for

example), respectively. If we denote with A

(t) the

number of bits generated by the source stream j in

the time interval [0, t], the function b

(t) represents

the arrival envelopes, and it verifies

j(t)

≤b

(t),

∀

t>0 (2)

Where A

(t) is a discrete random variable that

assumes values in the range [0, b

(t)], whose

statistical distribution is unknown.

The proposed model statistically characterizes

the traffic by means of the mean rate of the

transmission rate variance RV

(t) in the interval [0,

t]. Formally:

(t)= σ

(t)/t) φ

=lim

∞

(t)/t) (3)

In the hypothesis of a stationary process for the

stream j it has been demonstrated that the variance is

upper limited, according to the relation:

(t)≤((φ

(t))/t)-φ

(4)

An admission control algorithm can be applied

on a given link to the total traffic envelope obtained

as the sum of the envelopes related to the individual

traffic streams. Depending on the characterization of

the incoming traffic statistic, it is possible to

calculate (approximately, (Knightly, 1998)), the

probability that the permanence time D of a packet

in the considered network node be higher than a

given threshold d. This represents the violation

probability of the worst-case delay d on the

considered link, and is approximated by the

following expression:

P(D>d)≈

max

0≤t≤β

1/√(2π)exp[-(C(t+d)-μ(t))

/(2σ

(t))] (5)

where:

μ(t)=t·φ (6)

(t)=t

·RV(t) (7)

β=min{t>0|b

(t)≤Ct} (8)

β indicates the time instant in which the service

linear function associated with the link capacity C(t)

crosses the envelope (modeled with a piece-wise

function) of the arrival traffic. This is the same

interval in which, if the traffic followed the worst-

case, it would see its own packets getting into the

buffer and wait for having access to the interface,

therefore experiencing delay.

This violation probability is upper limited by the

probability of the total backlog, that is the total

amount of packets in the time interval d (the

predefined limit on the delay), which exceed the

maximum number of packets that can be served in

the same period.

In (6) an approximation for a large traffic

aggregate composed of statistically independent

source flows was applied. By the central limit’s

theorem, it is possible to assume a Gaussian

distribution of the difference between the backlog

and the available service at the concerned link

interface.

3 WORK DESCRIPTION

The work aims to investigate two weight updating

methods for a dynamic WFQ scheduler in order to

achieve proportional relative QoS guarantees. The

former, see subsect. 2.1, based on the resolution of a

linear system, while the latter on Knightly’s theory,

as described in the next subsection.

Comparisons have been carried out in the same

working conditions, parameter settings and network

scenarios, as well as target QoS assurances.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

3.1 A Dynamic WFQ Based on the

Knightly’s Theory

As stated in the previous paragraphs, the WFQ is the

concerned scheduling algorithm, enhanced with an

integrated method of measurement and

characterization of the traffic aggregates, which in

our context corresponds to the different classes of

service in a DiffServ-enabled 4G network, in order

to tune at run-time the weights of the different

queues.

In particular, for each traffic aggregate

distinguished by the DSCP value (Nichols, 1998),

the parameters of the characterizing traffic constraint

functions are measured or indirectly calculated.

Those parameters are: the mean rate, the burstiness,

the peak rate and the peak rate duration.

Actually, for an initial simulation analysis, the

updating mechanism is triggered by the result of an

effective statistical test (see subsect. 3.2) applied to

the average arrival rate only. The said test is

executed for all the incoming active aggregates at

the considered IP router interface. It is enough that

just one parameter (i.e. the average arrival rate in a

queue) presents a variation detected by the test (with

the assigned level of reliability), to force an updating

of the parameters of all the aggregates and a tuning

of the scheduler’s weights. If there’s no significant

change in a measurement period for the functional

parameters, the weights remain the same.

The newly proposed updating algorithm based on

Knightly’s theory has been designed with particular

attention to the number of operations to be executed.

The goal is to reduce as much as possible the

computational overhead, in order to have a solution

suitable even for broadband networks, where the

high value of the router service rate could entail

constraints on the complexity of the deployed

mechanisms.

The weight value for each queue is obtained

from a system of equations similar to (5) (subsect.

2.2), where the minimum service capacity to be

allocated to each queue is the parameter to calculate,

that in turns corresponds to the queue weight. Of

course, the system also fulfils the condition that the

sum of the bandwidth allocated to the queues must

be equal to the service rate of the router interface (in

(5) indicated as C

link

In practice, we have to deal with an N

order

equation, where the parameter d to be determined,

referring to the equation (5), represents the

maximum delay for the N

class (the class granted

with the best service in terms of delay). To be noted

that the maximum delay of each class can be

expressed in terms of the maximum delay of a given

class (in this case of the N

one) by means of the

assigned QoS factors.

This non-linear equation can be easily solved at

run time with an approximated algorithm based on

the well-known Newton iterative method that allows

to easily obtain the searched solution with a

configurable maximum error. More in detail, with an

extremely limited number of iterations (actually,

never more than 4), it is possible to determine the d

value with an error lower than a microsecond.

Newton’s algorithm needs an initial value for the

parameter to be determined. It is represented by the

value employed in the previous bandwidth allocation

(currently still valid).

Furthermore, we remind that the computational

overhead is dramatically reduced by the application

of the statistical test that leads to an updating

frequency of about 30% of the measurement

windows (with a reliability level of 90%).

3.2 An Effective Statistical Test

The t-Student test (Spiegel, 2000) application to a

set of empirical observations of rate values is

conditioned to the truth of the following

assumptions:

I. the samples are independent and with

identical distribution (iid)

II. the samples belong to a normal statistical

distribution.

Actually, by the Central Limit theorem (Spiegel,

2000) the test can be applied to whatever

distribution if the observation set is large enough (in

practice > 30).

The iid hypothesis is verified when the number

of observations is small compared to the population

cardinality (Spiegel, 2000).

With a proper measurement window length both

the assumption are valid (Cao, 2001)(Cao, 2002).

With a given reliability level, the test is positive

when the hypothesis “the traffic (i.e. the mean rate)

of a service class has not changed” is to be rejected.

3.3 Traffic Description and

Parameter Settings

We considered traffic aggregates composed of both

TCP and UDP flows. The latter, H.263 coded video

streams at different bit rates, ranging from 64 to 256

Kbit/s as mean value, generated by real traces

(H.263/MPEG4) of video streaming and

conferencing applications (see the table below for

more details). By their nature of typical compressed

video flows, the related bit rate is highly variable

with a burstiness factor (peak to mean rate ratio) of

even 10.

WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED FAIR QUEUING (WFQ) SCHEDULER

Table 1: Characteristics of a considered H.263 coded

video flow.

Encoder Input 176x144 pel (QCIF)

N° of pixels for Chrominance 88

Frame Rate 25 fps

Quantization Parameter 5

Pattern IBPBPBPBPBP

Integer pel search window 15 pels

Specifically, every traffic aggregate included 3

video streams at 64 Kbit/s and 12 video streams at

256 Kbit/s, for a total average rate (together with the

TCP flows) of about 22 Mbit/s.

For a second set of simulations, we also

generated H.264 JSCC/D compliant video flows

with a bit rate ranging from 60 to 320 Kbit/s. These

video flows concerns application scenarios such as

video-call, video on demand, video conference and

live news. More specifically, the related aggregate

included 16 video streams at 60 Kbit/s, 6 video

streams at 200 Kbit/s, 4 video streams at 220 Kbit/s

and 6 video streams at 320 Kbit/s for a total average

rate (together with the TCP flows) of about 22

Mbit/s.

The transmission interface was 100 Mbit/s (e.g.

from a FastEthernet network card), where a dynamic

WFQ scheduler managed 4 queues, each one fed

with a different aggregate and assigned with a QoS

factor equals to 1, 2, 3 and 4, respectively (i.e. the

traffic in the 4

queue granted with the best service

in terms of delay and loss).

For these simulation scenarios, we selected: a

time window measurement process of 1.8 s (Panza,

2005), a sampling period of 40 ms and a first-order

low pass filter having the zero (termed as k

parameter) equal to 0.95 in order to average the

gauged values. The measured magnitude is the

buffer filling for the weight updating method based

on the linear system resolution, whilst it is the

average arrival rate for the newly conceived one,

based on Knightly’s theory.

In the next section, we report and analyze the

simulation results, produced by means of OPNET

Modeler tool by OPNET Technology Inc..

4 SIMULATION RESULTS

4.1 Updating Method Based on the

Linear System

The t-Student test is applied in order to decrease the

weight update frequency. Of course, the actual

frequency depends on the traffic dynamic; but if the

last estimation of the traffic is still valid for all the

aggregates in the new time window, the queue

weights are not updated, thus saving computational

power.

The analysis has been carried out considering as

the measured and driving magnitude either the

buffer filling or the traffic mean rate, at the decision

times.

The minimum required buffer dimension in order

to avoid or bound the loss for that queue (when the

factors assigned to the other queue remain the same)

has been gauged both for the 99

and the 100

percentile of the delay. Of course, the latter value

corresponds to absence of loss. Even the average

delay in each queue and at the interface as a whole

are reported.

Table 2: Minimum buffer sizes for the 99

and 100

percentiles of the delay in the 4 queues.

Queue 99

perc. Min.

buffer size (bytes)

100

perc. Min.

buffer size (bytes)

1 89673 117963

2 75983 82864

3 59945 74254

4 55677 68501

Table 3: Average delay in each queue and at the interface

as a whole.

Queue Average Delay (ms) Average Delay at

the interface (ms)

1 1.808

2 0.934

3 0.701

4 0.549

0.998

It is worthwhile to point out that the statistical

test might not be applied, because the iid hypothesis

of the collected samples is not verified a priori (the

buffer dimension depends somehow on the story of

the system and this could introduce not negligible

correlation to be analyzed). Anyway, for the sake of

comparison between the two investigated weight

updating methods, we collected results with the test

application.

The 99

percentiles of the delay for the 4 queues

are 11.2, 6.7, 5.4 and 4.4 ms, respectively.

4.2 Updating Method Based on

Knightly’s Theory

For the sake of comparison, the same sources and

link were used for this set of simulations as in the

previous analysis (see subsect. 3.3). The driving

magnitude is the mean rate and the statistical test is

applied.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

The graphs below depict the packet-by-packet

averaged delay and the CDF (Cumulative

Distribution Function) of the delay in the 4 queues.

Figure 2: Average delay and CDF of the packet-by-packet

delay.

As expected, the delay differentiation is still in

line with the assigned quality of service factors to

each queue: the higher the factor the lower the delay.

This is true even for the packet-by-packet delay

when collected in a bucket mode (i.e. every point in

the graph corresponds to the mean delay value about

a given number of consecutive packets).

The tables below report the relevant figures for

the buffer size and the delay for the different queues.

Table 4: Minimum buffer sizes for the 99

and 100

percentiles of the delay in the different 4 queues.

Queue 99

perc. Min.

buffer size (bytes)

100

perc. Min.

buffer size (bytes)

1 91945 111755

2 64382 108775

3 45734 65190

4 18030 55257

Table 5: Average delay in each queue and at the interface

as a whole.

Queue Average Delay (ms) Average Delay at

the interface (ms)

1 1.772

2 1.087

3 0.445

4 0.221

0.884

The 99

percentiles of the delay are 14.12, 9.58,

4.29 and 1.82 ms, respectively for the 4 queues.

4.3 Results with JSCC/D Compliant

Traffic Flows

An analysis for both the scheduling systems was

carried out also when one out of the four queues

(specifically, the first one) was feed with a traffic

aggregate composed by JSCC/D compliant video

flows. For an effective comparison, exactly the same

parameters were used and results collected. The

following tables report the average delay for the four

queues and for the interface as a whole.

Table 6: Average delay in each queue and at the interface

as a whole with the former weight updating algorithm.

Queue Average Delay (ms) Average Delay at

the interface (ms)

1 1.60

2 1.02

3 0.77

4 0.53

0.98

Table 7: Average delay in each queue and at the interface

as a whole with the Knightly’s theory based weight

updating algorithm.

Queue Average Delay (ms) Average Delay at

the interface (ms)

1 1.78

2 1.04

3 0.53

4 0.265

0.9

The graphs below depict the CDF of the delay in

the 4 queues obtained with the former scheduler and

the latter based on Knightly’s theory, respectively.

WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED FAIR QUEUING (WFQ) SCHEDULER

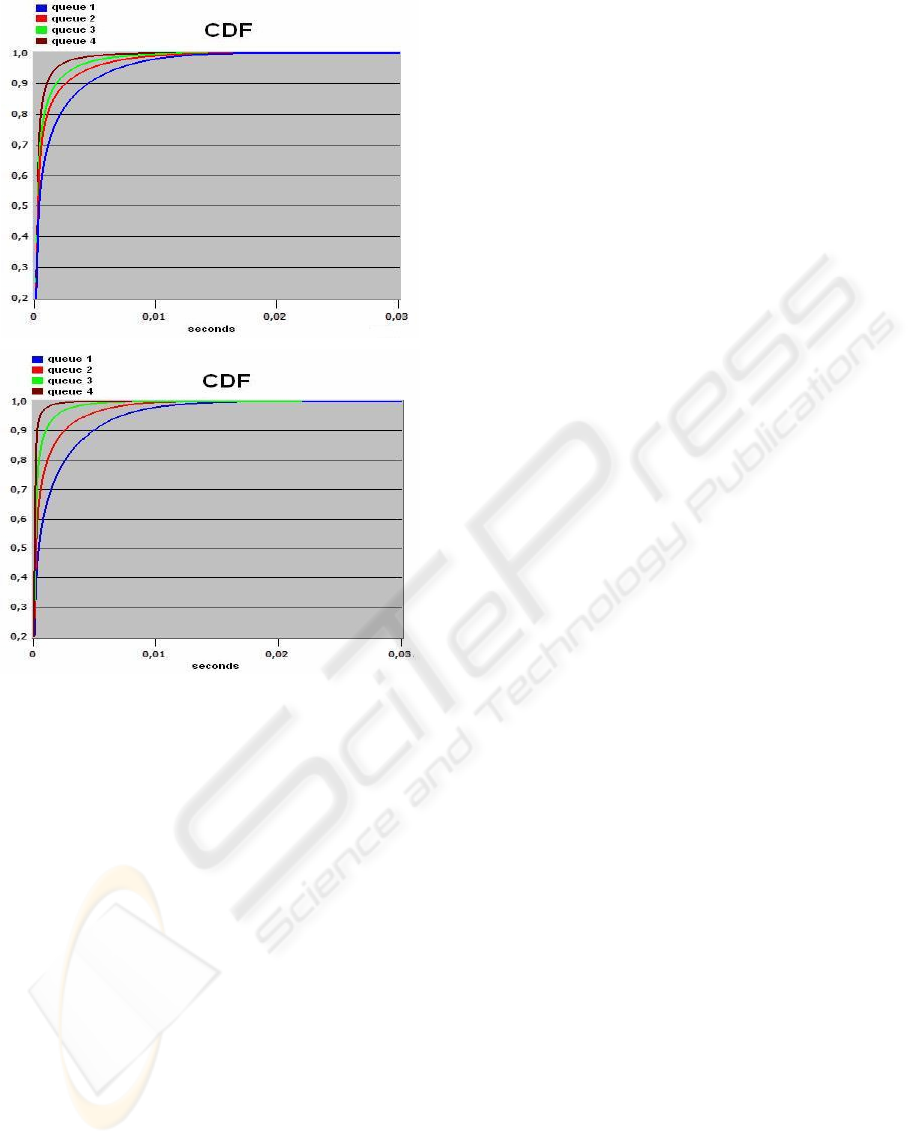
Figure 3: CDF of the delay when the weight updating

algorithm is either based on the linear system or

Knightly’s theory.

The 99

percentiles of the delay are 12.3, 10.0,

7.9 and 5.0 ms, respectively for the 4 queues when

the weight updating algorithm is based on the linear

system, and 12.57, 8.47, 4.76 and 1.92 ms, when the

weight updating is based on Knightly’s theory.

4.4 Analysis

The collected results about the buffer dimension and

the delay confirm the consistency of the designed

systems. A dynamic version of the WFQ scheduler

based on either the investigated weight updating

methods can provide QoS guarantees according to a

proportional relative model. The higher the assigned

quality of service factor to a given queue, the lower

the delay and the minimum required buffer

dimension in order to avoid or bound the loss for

that queue (when the factors assigned to the other

queue remain the same).

More specifically, we can observe that the traffic

aggregates in the 3

and 4

queues (those assigned

with the greatest QoS factors) are granted a lower

delay when the updating is based on Knightly’s

theory, but the contrary happens to the 1

and 2

queues. Such results are also confirmed by the

measurements about the buffer dimension.

Therefore, with the novel and more sophisticated

method a higher delay differentiation is provided

among classes of service.

Looking at the ratio between the figures of the

different queues for both the delays and the buffer

dimension, we can state that the weight updating

based on Knightly’s theory more effectively

differentiates the QoS provided to the different

traffic aggregates, which is more in line with the

assigned QoS factors.

The newly proposed weight updating mechanism

can provide a better differentiation in terms of

granted delays to the various configured classes of

service. This means higher performance in terms of

supporting a proportional relative model for QoS.

However, also the first mechanism achieves

good results, with a lower computational overhead.

5 CONCLUSIONS

In this work, we have investigated and analyzed two

different weight updating methods for a dynamic

version of the WFQ scheduler, i.e. where the

weights are tuned at run-time according to both the

actual traffic that enters each queue and the mutual

ratio between the QoS factors assigned to the

concerned classes of service at the considered IP

router interface.

A simulation analysis has been carried out in

network scenarios and with configuration parameters

suitable for DiffServ-enabled 4G networks.

Novel proposals for an updating method based

on the Knightly’s theory and the idea of applying a

statistical test able to save computational power,

have been described and deployed.

By analyzing the collected results about the

delays (99

percentile and average value) granted to

the various service classes and the buffer dimension

(to lose only the packets that experience a delay

greater than the 99

percentile or not at all), we can

conclude that the weight updating method based on

the Knightly’s theory is able to provide a better

differentiation in terms of granted delays to the

various configured classes of service, that is, higher

performance in terms of supporting a proportional

relative model for QoS. This has been verified with

traffic aggregates composed of either traditional

(non adaptive) or JSCC/D compliant video streams.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

However, also the method built on a simple

system of linear equations achieves good results,

with a lower computational overhead.

The better selection between them, really

depends on the specific network scenario, the

required QoS guarantees for the classes of service to

be supported and the available computational

resources.

REFERENCES

PHOENIX: FP6 IST European project. http://www.ist-

phoenix.org/

Panza, G., Grazzioli, M., Sidoti, F., 2005. Design and

analysis of a dynamic Weighted Fair Queueing (WFQ)

scheduler. IST Mobile’05

Wroclawski, J., 1997. The Use of RSVP with IETF

Integrated Services, RFC 2210. IETF intserv WG.

September 1997

Nichols, K. et Al., 1998. Definition of the Differentiated

Services Field (DS Field) in the IPv4 and IPv6

Headers, RFC 2474. IETF diffserv WG. December

1998

Blake, S. et Al., 1998. An Architecture for Differentiated

Services, RFC 2475. IETF diffserv WG. December

1998.

Dovrolis, C., Ramanathan, P., 1999. A Case for Relative

Differentiated Services and the Proportional

Differentiation Model, ACM SIGCOMM. Sept. 1999

Li, C-C., Tsao S-L., Chen, M. C., Sun, Y., Huang, Y-M.,

2000. Proportional Delay Differentiation Service

Based on Weighted Fair Queuing, Computer

Communications and Networks. 2000

Keshav, S., 1997. An Engineering Approach to Computer

Networking., Addison-Wesley professional computing

series. 1997

Kun Pang Xiaokang Lin Junli Zheng Xuedao Gu Nat.,

2000. Dynamic WFQ scheduling for real-time traffic

in wireless ATM links, Communication Technology

Proceedings. 2000

H.263/MPEG4-compressed video traces: http://www-

tkn.ee.tu-berlin.de/research/trace/trace.html

Knightly, E. W., 1997. Second Moment Resource

Allocation in Multi-Service Networks, in Proceedings

of ACM SIGMETRICS '97. Seattle, WA. June 1997

Knightly, E. W., 1998. Enforceable Quality of Service

Guarantees for bursty traffic streams, in IEEE

Infocom ,pag. 635-642, March 1998

Spiegel, M., Schiller, J., Srinivasan, R., 2000. Probability

and Statistics, second edition, McGraw Hill. 2000

Cao, J., Cleveland, W. S., Lin, D., and Sun, D. X., 2001.

Internet Traffic Tends Toward Poisson and

Independent as the Load Increases, Bell Labs Tech

Report. 2001

Cao, J., Cleveland, W. S., Lin, D., and Sun, D. X., 2002.

The Effect of Statistical Multiplexing on the Long

Range Dependence of Internet Packet Traffic, Bell

Labs Tech Report. 2002

WEIGHT UPDATING METHODS FOR A DYNAMIC WEIGHTED FAIR QUEUING (WFQ) SCHEDULER