
REAL-TIME IMAGE WAVELET CODING FOR LOW BIT RATE
TRANSMISSION
Gaoyong Luo
Faculty of Technology, Buckinghamshire Chilterns University College, Queen Alexandra Road, High Wycombe,
Buckinghamshire HP11 2JZ, UK.
Keywords: Image embedded coding, Edge preservation, Local variance analysis, Bit rate allocation, Error resilience.
Abstract: Embedded coding for progressive image transmission has recently gained popularity in image compression
community. However, current progressive wavelet-based image coders tend to be complex and
computationally intense requiring large memory space. The encoding process usually sends information on
the lowest-frequency wavelet coefficients first. At very low bit rates, images compressed are therefore
dominated by low frequency information, where high frequency components belonging to edges are lost
leading to blurring the signal features. This paper presents a new image coder for real-time transmission,
employing edge preservation based on local variance analysis to improve the visual appearance and
recognizability of compressed images. The analysis and compression is performed by dividing an image
into blocks. Lifting wavelet filter bank is constructed for image decomposition and reconstruction with the
advantages of being computationally efficient and boundary effects minimized. A modified SPIHT
algorithm with more bits used to encode the wavelet coefficients and transmitting fewer bits in the sorting
pass for performance improvement, is used to reduce the correlation of the coefficients at scalable bit rates.
Local variance estimation and edge strength measurement can effectively determine the best bit allocation
for each block to preserve the local features. Experimental results demonstrate that the method performs
well both visually and in terms of quantitative performance measures, and offers error resilience feature that
is evaluated using a simulated transmission channel with random error.
1 INTRODUCTION
The advent of multimedia computing has led to an
increased demand for digital images (Hilton et al.,
1994). The transmission of digital images is rapidly
becoming popular on mobile telephones, personal
digital assistant (PDA) technology and other
wireless based image service. However, transmitting
digital images via mobile device is often subject to
bandwidth or cost constraints which are
incompatible with high data rates. The demand for
better quality images, means that effective and fast
data compression techniques are essential for real-
time transmission. In order to obtain the required
degree of compression, lossy coding techniques have
to be utilized (Pearlman, 2001). The current lossy
JPEG image compression standards enjoy success
due to its low complexity in implementation and its
reasonable performance. However, when high
compression ratio is needed (i.e., at lower bit rates),
annoying blocking artifacts appear. The
development of the lapped orthogonal transform
(LOT) (Malvar, 1992) and its generalized version
GenLOT (de Queiroz et al., 1996) helps solve the
blocking problem to a certain extent at the price of
increasing computational complexity.
More recently, the wavelet transform has emerged
as a cutting edge technology, within the field of
image compression. Wavelet-based coding (Vetterli
and Kovacevic, 1995) provides substantial
improvements in picture quality at higher
compression ratios (Meyer et al., 2002; Claypoole et
al., 2003; Rajpoot et al., 2003). The introduction of
the embedded zero-tree concept (Shapiro, 1993) for
wavelet-based image compression has generated a
significant improvement in performance. In recent
years embedded coding has gained popularity in
image compression community due to its simplicity,
high performance and nice properties. Some
representative works of embedding include the
embedded zerotree wavelet coding (EZW) (Shapiro,
1993), the set partitioning in hierarchical trees
(SPIHT) (Said and Pearlman, 1996), the embedded
block coding with optimized truncation (EBCOT)
157
Luo G. (2006).
REAL-TIME IMAGE WAVELET CODING FOR LOW BIT RATE TRANSMISSION.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 157-163
DOI: 10.5220/0001569901570163
Copyright
c
SciTePress

(Taubman, 2000), and set partitioning embedded
bloCK (SPECK) (Pearlman, et al., 2004). EBCOT
was adopted as the basic algorithm in the JPEG 2000
image compression standard (Adams, 2002), which
is a fairly complex and computationally intense
procedure. The ability to adjust the compression
ratio by simply truncating the coding bitstream
makes embedding very attractive for a number of
applications such as progressive image transmission
and low delay image communication (Li and Lei,
1999). However, current progressive wavelet-based
image coders tend to send information on the
lowest-frequency wavelet coefficients first
(Schilling and Cosman, 1999). Such images have
most of their energy in the low frequency bands. In
wavelet domain, the energies of high frequency
coefficients are mainly concentrated around edges in
an image (Ye et al., 2004). In lossy image
compression, most high frequency part of the image
will be removed. The removal causes the edges of
the image to be blurred (Lay and Wang, 2005). At
very low bit rates, images compressed by these
coders are therefore dominated by low frequency
information, where high frequency components
belonging to edges are lost leading to blurring the
signal features. These effects combine to hamper
recognition of objects in the images. This paper
presents a fast image coder with error resilience by
block processing and employing edge preservation
based on local variance analysis to improve the
visual appearance and recognizability of compressed
images at very low bit rates.
2 LIFTING WAVELET FILTER
BANK
Over the last decade wavelets have been applied
successfully in many diverse fields. The need for
improvement of wavelets comes from a shortcoming
that is inherent because of its construction. Second
generation wavelets named when the concept of
lifting was introduced (Sweldens, 1996; Sweldens,
1998), open a new direction to construct wavelets
which are not necessarily translates and dilates of
one fixed function. The lifting scheme makes
optimal use of similarities between the high and low
pass filters so as to achieve a faster implementation
of wavelet transform (WT). The flexibility afforded
by the lifting scheme allows the basis functions
associated with wavelet coefficients near a
window’s boundaries to change their general shape
at the boundaries. In this manner, a basis function
more accommodating to a boundary can be used to
minimize boundary effects.
Classical implementation of WT uses two band
filter bank with recursion on its low pass (LP). This
can be represented by its equivalent polyphase
matrix
~
()Pz
, which is assembled from even and odd
filter components. With
det[ ( )]Pz = 1
, it always exist
factorisation of
P
z
()
(Daubechies and Sweldens,
1998):
Pz
K
K
sz
tz
i
i
im
()
()
()
=
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎩
⎫
⎬
⎭
=
∏
0
0
1
1
01
10
1
1
(1)
Equation (1) allows ladder realization of
~
()Pz
by
reversible lifting steps followed with normalization
by factor
K
as shown in Figure1.
Figure 1: Ladder structure of lifting steps.
Signal is partitioned into even and odd
components that are then mutually predicted by
t
i
and updated by
s
i
. After normalization the algorithm
is recursively applied to LP part. Based on the
structure of one dimensional (1D) wavelet
transform, two dimensional (2D) lifting steps that
can be used for predict/update steps on lattices, can
then be built. The algorithm developed uses
weighted coefficients of lifting factorisation of 1D
prototype transform, but replacing 1D
neighborhoods by 2D rings (Vargic, 1998). Weight
i
w
for lifting coefficient depends on number of
pixels in actual ring:
ringthiinpixelsofnumber
i
w
−
=
2
(2)
Thus 2D version of forward predict/update steps can
be expressed as follows:
{
}
{}
∑∑
∑∑
+=
+=
j
st
yxjk
k
k
st
k
st
yx
st
yx
j
st
yxjk
k
k
st
k
st
yx
st
yx
sringwss
dringwdd
)(
,,
)()(
,
)(
,
)(
,,
)()(
,
)(
,
β
α
(3)
where st = 1…m (m is number of predict/update
steps),
{
}
centerring
jk,
is 2D neighborhood operator
which returns value of j-th point in k-th
neighborhood of
cente
r
,
)(st
k
α
and
)(st
k
β
are lifting
coefficients associated with actual predict/update
step and k-th neighborhood of
cente
r
,
w
k
is weight
for k-th ring. Thus 2D versions of biorthogonal
filters can be constructed. To implement them, the
parameters
)(st
k
α
and
)(st
k
β
need to be derived. In this
study, symmetric biorthogonal wavelet is required
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
158
for perfect reconstruction. Thus 9/7 filter pair for
fast computation can be used. This filter pair is
smooth and relatively short. The analysis low pass
filter has 9 coefficients, while the synthesis high
pass filter has 7 coefficients. The mathematical
property of symmetry and compact support with 4
vanishing moments in both analysis and synthesis
high pass filters, provides the advantages of 9/7 filter
bank over other wavelet families in many
applications. The factoring process of 9/7 filter pair
starts from the analysis filter
0
1
2
22
4
)()()(
~
hzzhzzhzh
e
++++=
−−
)1()()(
~
1
12
3
+++=
−
zhzzhzh
o
(4)
The lifting coefficients can be computed as
31400
/2 hhhhr −=
,
314421
/ hhhhhr −
−
=
,
103310
/ rrhhhs −−=
,
100
2rrt
−
=
The 2D wavelet filter bank can then be implemented
with boundary effects minimized by changing
wavelet shape for handling filtering near the
boundaries using:
34
)1(
1
/ hh=
α
,
13
)1(
1
/ rh=
β
01
)2(
1
/ sr
=
α
,
00
)2(
1
/ts=
β
,
0
tK
=
3 EMBEDDED CODING
The wavelet transform (WT) provides an efficient
representation of image data for compression. The
structure of spatial orientation trees by wavelet
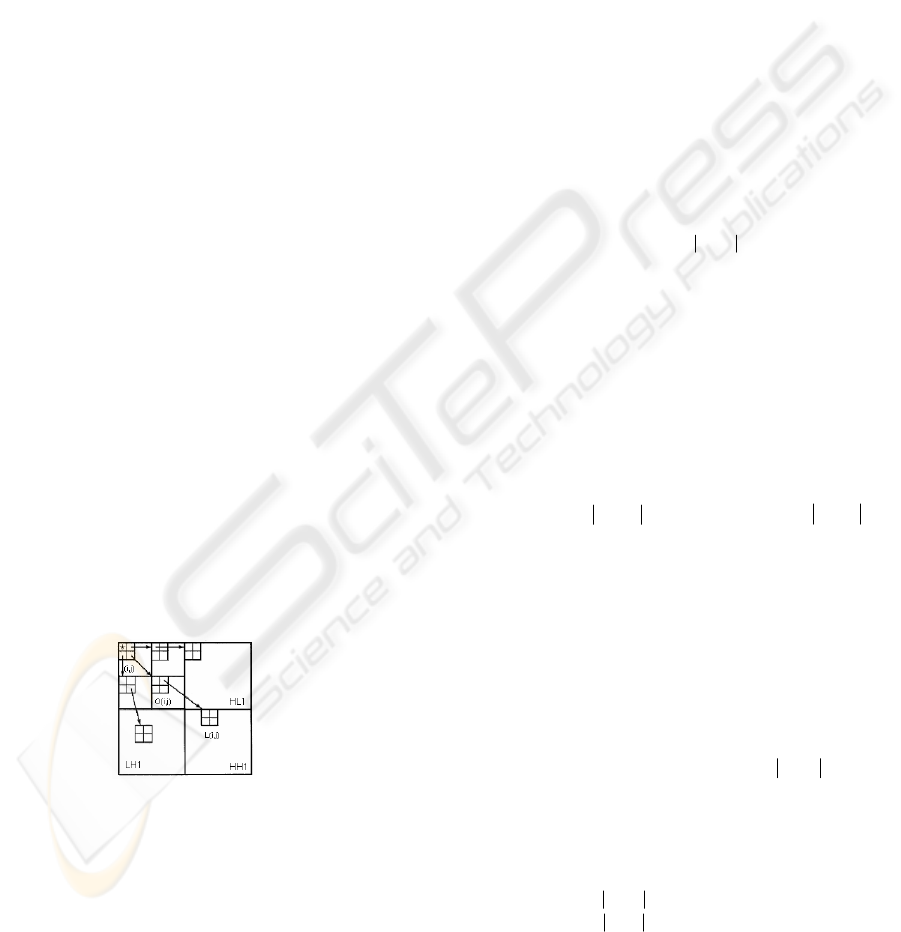
decomposition is shown in Figure2 with LH1, HL1,
HH1 in the highest frequency band.
WT localizes
signal energy in both frequency and spatial domains,
and large wavelet coefficients in different frequency
subbands tend to be produced at the same spatial
location. This correlation can be reduced by a
modified SPIHT algorithm.
Figure 2: Spatial orientation trees.
3.1 Modified SPIHT
SPIHT (Said and Pearlman, 1996) builds on the
principle that spectral components with more energy
content should be transmitted. It is provided with an
order of the coefficients defined in the form of trees
as shown in Figure2, where
),(
j
iO
={the 4 offspring
of coordinates
)},{(
j
i
},
),(),(),(
j
iO
j
iD
j
iL −=
,
),(
j
i
D
={all
descendants of coordinates
)},{(
j
i
}. The algorithm
employs a number of linked lists (LIP-list of
insignificant pixels, LSP-list of significant pixels,
LIS-list of insignificant sets) which are manipulated
according to a significance test that is at first applied
to sets and then eventually to individual coefficients.
The algorithm tests available coefficients and sets of
coefficients to determine if those coefficients whose
magnitudes are greater than the threshold
n
2
. The
encoder output consists of sorting information that is
required to identify the significant coefficients with
respect to an actual bitplane and refinement
information for enhancing the accuracy of
significant coefficients. To save bits for encoding
coefficients, a modified SPIHT is developed by
simplifying the header stream and transmitting fewer
bits in the sorting pass. In the header stream, the
logarithm of the maximum value of wavelet
coefficients (
})),({(maxlog
)},{(2max
jidn
ji
=
) is calculated
and rounded into integer to allocate bits for coding at
the beginning of the encoder output bitstream.
Information such as the matrix dimension and the
number of wavelet decomposition levels, is set to
reside in the encoding and decoding algorithm, so
that more bits can be used for coefficient coding.
The reconstruction quality level thus is increased
with more bits containing signal information. In the
sorting pass, the maximum values of coefficients in
logarithm at
),(
j
iO
and
),(
j
iL
are calculated as
})),({(maxlog
)},{(2
jiOn
jiO
=
,
})),({(maxlog
)},{(2
jiLn
jiL
=
.
The significant tests compare
n
with
O
n
and
L
n
. If
n
is
greater than
O
n
and
L
n
, then it is not necessary to
check
),(
j
iO
and
),(
j
iL
because they are insignificant.
In the case when at least one of the coefficients at
),(
j
iO
is significant but all coefficients at
),(
j
iL
are not,
the sorting pass can be improved by transmitting
fewer bits. The procedure of the modified SPIHT is
as follows:
(1) Initialization: output
})),({(maxlog
)},{(2
jidn
ji
=
LSP={}
LIS={
),(|),( jiji
has descendants and is in the
lowest level subband}
LIP={
),(|),( jiji
is in the lowest level subband}
})),({(maxlog
)},{(2
jiOn
jiO
=
})),({(maxlog
)},{(2
jiLn
jiL
=
(2) Sorting Pass:
LIP-processing
For each
)},{(
j
i
in LIP:
REAL-TIME IMAGE WAVELET CODING FOR LOW BIT RATE TRANSMISSION
159

if
)},{(
j
i
is significant
output 1 and the sign of the coefficient then
move
)},{(
j
i
to LSP.
else
output 0.
LIS-processing
For each
)},{(
j
i
in LIS:
if
)},{(
j
i
is significant
process the children of
)},{(
j
i
differently
depending on
O
n
and
L
n
.
else
ouput 0
(3) Refinement Pass:
output the n-th bit of the coefficients in LSP
added prior to this round.
(4) Quantization-step Update:
decrement n by 1 and repeat step (2) to (4).
3.2 Bit Allocation and Error
Resilience
The modified SPIHT is used to reduce the
correlation of wavelet coefficients and encode the
data into bit streams. As images from different
categories tend to show different spatial domain
characteristics. An area with the smallest variation
represents a homogeneous region, while regions
containing edges will have a higher variance than
more homogeneous regions. In order to improve the
visual appearance and recognizability of compressed
images at very low bit rates, an image can be divided
into 64 x 64 pixel blocks (large images can have
bigger block sizes), and each block can be
transformed into wavelet domain. Local variance
estimation and edge strength measurement can be
used to effectively determine the best bit rate
allocation for each block to preserve the local
features of the original image corresponding to the
boundaries of the objects by assigning more bits for
blocks with higher variance and edge strength. To
take advantage of local analysis, block size tends to
be small. However too small size does not allow
wavelet decomposition in enough levels required by
wavelet based image compression. The size of 64 is
a balance having maximum 5-level spatial-frequency
decomposition. Local variance and edge analysis is
based on the block in wavelet and image domain.
The development of lifting wavelet filter bank for
spatial-frequency decomposition and reconstruction
of images, not only speeds up the calculation, but
also minimises the boundary effects. This allows
local variance and edge analysis to be performed for
bit allocation. For a given block j the bit allocation
factor can be expressed as:
Xj
σ
ε
λ
=
(5)
where
ε
is the measure of the image edge strength ,
2
X
σ
is the local estimated signal variance on the
subband considered. The noise variance is estimated
as the median absolute deviation of the diagonal
detail coefficients on level 1 (highest frequency
subband
1
HH
32 x 32 block) (Chang et al., 2000):
6745.0
)(
ij
WMedian
=
σ
,
1
HHsubbandij
W
∈
(6)
The estimate of the signal standard deviation is
)0,max(
2
2
σσσ
−=
WX
(7)
where
∑
=
=
n
ji
ijW
W
n
1,
2
2
2
1
σ
,
2
W
σ
is an estimate of the
variance of the observations, with
nn ×
being the
size of the wavelet coefficients on the subband under
consideration. In case
2
2
W
σσ
≥
, all coefficients from
the subband are set to zero. The local edge strength
is measured by using image gradient (Saha and R.
Vemuri, 2000):
[
]
∑∑ ∑∑
== ==
+−−+−
∗
=
63
1
64
1
64
1
63
1
)1,(),(),1(),(
6464
1
ij ij
jifjifjifjif
ε
(8)
where
),( jif
is image pixel value. The measure
indicates how busy the image is in terms of the
number of edges and contours in it.
Variance and edge measure are locally computed
at each block. The bit allocation for block j is
BB
M
j
j
j
j
∑
=
=
1
λ
λ
where B is the total bit number for all the wavelet
coefficients to encode, M is the total number of
image blocks to divide. Each block is encoded into
j
B
bits. This allows more bits to be allocated to regions
containing edges and having a higher variance, and
fewer bits to areas with small variation representing
homogeneous regions, such that high frequency
components belonging to edges and local features of
the original image can be preserved.
To save the bits for transmitting maximum value
of wavelet coefficients and bit number for each
block, their logarithms are calculated and the
differences from the maximum of all the blocks are
stored to form an image matrix:
(1) If
642
≤
M
, the image size is 8x8, padding 0 if
data length is not enough.
(2) If
1282
≤
M
, the image size is 8x16, padding 0
if data length is not enough.
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
160

(3) If
2562 ≤
M
, the image size is 16x16, padding
0 if data length is not enough.
(4) If
2562 >
M
, using bigger block size
Using the 2D lifting wavelet filter bank and the
modified SPIHT, the image can be encoded into 32
bits and transmitted in the header stream. The
decoded data will be used for bit allocation for each
block to keep the overall bit rate constant.
Error resilience is one of the most desirable
properties in real-time transmission applications.
Using fast SPIHT embedded coding, it is much
easier to design efficient error-resilient schemes
(Yang and Cheng, 2000; Alatan et al., 2000) for
error protection. This is because with embedded
coding the information is sorted according to its
importance, and the requirement for powerful error
correction codes decreases from the beginning to the
end of the compressed data. If an error is detected,
but not corrected, the decoder can discard the data
after that point and still reconstruct the signal
obtained with the bits received before the error.
Also, with bitplane coding the error effects are
limited to below the previously coded planes. In the
face of transmission errors, joint source-channel
SPIHT coding scheme for unequal error protection
can be easily designed by varying both source
coding bit rate and channel coding redundancy with
added complexity and delay depending on the
channel error degree.
4 EXPERIMENTAL RESULTS
AND DISCUSSION
2D lifting wavelet filter bank by changing wavelet
shape at the boundaries was developed for fast
implementation of spatial-frequency decomposition
and reconstruction with boundary effects minimized.
A modified SPIHT algorithm is used to encode
wavelet coefficients at each block, which gives more
efficient implementation both in terms of memory
usage and execution time. In some situations, an
image may be quite large in comparison to the
amount of memory available to the codec.
Consequently, it is not always feasible to code the
entire image as a single atomic unit. Image tiling
reduces memory requirements and allows better bit
allocation based on image contents, and since they
are also reconstructed independently, they can be
used for decoding specific parts of the image instead
of the whole image.
To demonstrate the proposed coder, a standard
Einstein image was used (with size of 512 x 512 for
all the example images). The quality of the
compression can be objectively evaluated using the
peak signal-to-noise-ratio (PSNR) defined below.
For a given reconstructed image
),(
ˆ
jif
of image
),( jif
,
the PSNR on dB scale is
2
11
2
10
)),(
ˆ
),((
1
))],([max(
log10
∑∑
==
−
=
I
i
J
j
jifjif
I
J
jif
PSNR
where I,J is the image size.
(a) (b) (c)
Figure 3: Einstein image (a) original (b) reconstructed by
SPIHT (c) reconstructed by proposed coder.
(a) (b) (c)
Figure 4: Boat image (a) original (b) reconstructed by
SPIHT (c) reconstructed by proposed coder .
(a) (b) (c)
Figure 5: Bird image (a) original (b) reconstructed by
SPIHT (c) reconstructed by proposed coder .
(a) (b) (c)
Figure 6: Car image (a) original (b) reconstructed by
SPIHT (c) reconstructed by proposed coder.
As SPIHT, in the term of compression efficiency
versus implementation complexity, is still the most
successful image coding method to date, the SPIHT
wavelet coder with 9/7 filters and 5-level
REAL-TIME IMAGE WAVELET CODING FOR LOW BIT RATE TRANSMISSION
161
decomposition is used here as a reference of the state
of the art coder. Figure3 shows the reconstructed
images using SPIHT coder and the proposed coder
by compression at the bit rate of 0.05 bpp (bits per
pixel). It can be seen that the decoded SPIHT image
is more blurred. Some edges preserved by the
proposed coder are lost by the SPIHT algorithm. It is
worth noting that, blocking artifacts is not noticeable
as block boundary effects are minimized by
changing wavelet shape at the boundaries. Table 1
lists the test results of Einstein image at different bit
rates (0.01, 0.05, 0.1, 0.25 and 0.5 bpp) in terms of
PSNR. Notice that the proposed coder performs
better than SPIHT at low bit rates, but when bit rates
increase SPIHT performs better. Another standard
Boat image with more edges across the image (more
difficult to compress) was used for comparison.
Figure4 shows the decoded images at 0.08 bpp. It is
noted that both coder achieved similar results,
although the proposed one performs slightly better.
Further examples are given using color images
compressed at low bit rates with similar
reconstruction quality. Figure5 shows a Bird image
with fewer edges across the image and the decoded
images at bpp. Figure6 shows a Car image with
more edges across the image and the decoded
images at 0.12 bpp. For comparison, test results are
summarized in Table 2. It can be seen that the
proposed coder outperforms SPIHT and the edges
are better preserved. The evaluation of the algorithm
indicates that the proposed coder outperforms
SPIHT at very low bit rates, both visually and in
terms of the quadratic error.
Table 1: PSNR (dB) of Einstein image at different bit
rates.
Bit Rate (bpp) SPIHT with 9/7 filters Proposed Coder
0.01 20.49 20.97
0.05 25.43 26.14
0.1 28.78 28.69
0.25 32.85 32.64
0.5 36.81 35.98
Memory usage is an important issue for image
coder, especially for large images and
implementation in small devices. The most common
method is to partition the image into stripes or tiles
and encode these partitions independently. The
proposed coder is based on block processing using
fast wavelet transform and modified SPIHT and
encoding different parts of an image with different
bit rates depending on their importance. This allows
the encode and decode to be processed in parallel,
microscopic parallelism at the level of individual
coding passes and more efficient hardware
implementations thus can be exploited for real-time
applications.
Table 2: PSNR (dB) of Einstein, Boat, Bird, Car image at
low bit rates.
Image Bit Rate (bpp) SPIHT with 9/7 filters Proposed Coder
Einstein 0.05 25.43 26.14
Boat 0.08 25.18 25.85
Bird 0.1 25.51 26.32
Car 0.12 25.41 26.19
To evaluate the error resilience features of the
proposed codec in the absence of channel coding,
the test image was decoded one hundred times each
over simulated transmission channel with random
errors. Bitstream header is transmitted without
errors. The average reconstructed image quality after
decompression was evaluated and shown in Table 3.
As can be seen, the reconstructed image quality
under transmission errors is still high at moderately
low error rates (i.e.
6
10
−
) and does not decrease
quickly when error rates increase at low bit rates.
This is due to the fact that the coder transmits the
most important information first for each block, and
the decoder can discard the data after that point and
still reconstruct the image obtained with the bits
received before the error. When the error rate is
high, almost all blocks are affected. For a particular
bitplane in a block, lower bitplanes may not be
decoded and therefore useless, but the whole image
can still be reconstructed with some block
information missing. In other words, the error
resilience of the codec decreases moderately with an
increase in error rates. Thus joint source-channel
coding scheme for unequal error protection can be
designed with added complexity and delay
depending on the channel error degree.
Table 3: PSNR in dB corresponding to the average of the
test Einstein image by averaging 100 runs of the decoded
data when transmitted over a noisy channel with various
bit error rates (BER) at low bit rates.
Bit Rate (bpp)
BER (
6
10
−
)
BER (
5
10
−
)
BER (
4
10
−
)
0.01 20.08 19.23 17.96
0.05 24.89 22.78 19.92
5 CONCLUSIONS
Two dimensional (2D) fast lifting wavelet filter bank
using lifting steps for predict/update steps on lattices
with 2D rings, was developed with the advantages of
being computationally efficient and boundary effects
minimized by changing wavelet shape for handling
filtering near the boundaries. Images from different
categories with different spatial domain
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
162

characteristics thus can be coded by a modified fast
2D SPIHT algorithm with more bits used to encode
the wavelet coefficients and transmitting fewer bits
in the sorting pass for performance improvement.
The compression is performed based on block
processing with local variance estimation and edge
strength measurement for the determination of the
best bit allocation to preserve the local features of
the original image corresponding to the boundaries
of the objects by assigning more bits for blocks with
higher variance and edge strength. Experimental
results demonstrate that the proposed image coder is
fast with error resilience and provides superior
image quality, both objectively and subjectively, at
very low bit rates, and is suitable for real-time
applications with less memory requirements.
REFERENCES
Adams, M.D., 2002. The JPEG-2000 Still Image
Compression Standard
, ISO/IEC JTC 1/SC 29/WG 1
N 2412.
Alatan, A.A., Zhao, M., and Akansu, A.N., 2000. Unequal
error protection of SPIHT encoded image bit streams,”
IEEE Journal on Selected Areas in Communications,
Vol. 18, No. 6, pp. 814-818.
Chang, S., Yu, B., and Vetterli, M., 2000. Adaptive
wavelet thresholding for image denoising and
compression. IEEE Transactions on Image
Processing
, Vol. 9, No. 9, 1532-1546.
Claypoole, Davis, G.M., Sweldens, W., and Baraniuk, R.,
2003. Nonlinear wavelet transforms for image coding
via lifting.
IEEE Transactions on Image Processing,
Volume: 12, Issue: 12, pp 1449-1459.
Daubechies, I., and Sweldens, W., 1998. Factoring
wavelet transforms into lifting steps.
J. Fourier Anal.
Appl.
4(3), 247-269.
de Queiroz, R., Nguyen, T.Q., and Rao, K., 1996. The
GenLOT: generalized linear-phase lapped orthogonal
transform.
IEEE Transactions on Signal Processing,
vol. 40, pp. 497-507.
Hilton, M.L., Jawerth, B.D., and Sengupta, A., 1994.
Compressing still and moving images with wavelets.
Multimedia Systems, Volume 2, Issue 5, pp 218–227.
Lay, K.-T., and Wang, L.-J., 2005. Image coding with
optimal wavelet packet and greedy edge enhancement.
Proceedings of the First International Conference on
Systems and Signals
(ICSS), Kaohsiung, Taiwan.
Li, J., and Lei, S., 1999. An embedded still image coder
with rate-distortion optimization. IEEE Transactions
on Image Processing
, Vol. 8, No. 7, pp 913-924.
Malvar, H.S., 1992.
Signal Processing with Lapped
Transforms
, Norwood, MA, Artech House.
Meyer, F.G., Averbuch
,, A.Z., and Coifman, R.R., 2002.
Multilayered image representation: application to
image compression. IEEE Transactions on Image
Processing
, Vol. 11, No. 9, pp 1072-1080.
Pearlman, W.A., 2001. Trends of tree-based, set
partitioning compression techniques in still and
moving image systems.
Proceedings of 22
nd
Picture
Coding Symposium
(PCS-2001), Seoul, Korea, pp 1-8,
25-27.
Pearlman, W.A., Islam, A., Nagaraj, N., and Said, A.,
2004. Efficient, low-complexity image coding with a
set-partitioning embedded block coder. IEEE
Transactions on Circuits and Systems for Video
Technology
, Vol. 14, pp 1219-1235.
Rajpoot, N.M., Wilson, R.G., Meyer, F.G., and Coifman,
R.R., 2003. Adaptive wavelet packet basis selection
for zerotree image coding.
IEEE Transactions on
Image Processing
, Vol. 12, No. 12, pp 1460-1472.
Saha, S., and Vemuri, R., 2000. An analysis on the effect
of image features on lossy coding performance. IEEE
Signal Processing Letters
, Volume: 7, pp 104-107.
Said, A., and Pearlman, W., 1996. A new, fast and
efficient image codec based on set partitioning in
hierarchical trees.
IEEE Transactions on Circuits and
Systems for Video Technology
, Vol. 6, pp 243–250.
Schilling, D., and Cosman, P.C., 1999. Edge-enhanced
image coding for low bit. Proceedings of International
Conference on Image Processing
(ICIP '99), Volume
III, Kobe, Japan, IEEE Computer Society, pp 747-751.
Shapiro, J., 1993. Embedded image coding using zerotree
of wavelet coefficients.
IEEE Transactions on Signal
Processing
, Vol. 41, pp 3445–3462.
Sweldens, W., 1996. The lifting scheme: A custom-design
construction of biorthogonal wavelets. Appl. Comput.
Harmon. Anal.
3(2), 186-200.
Sweldens, W., 1998. The lifting scheme: A construction of
second generation wavelets. SIAM J. Math. Anal.
29(2), 511-546, 1998.
Taubman, D., 2000. High performance scalable image
compression with EBCOT. IEEE Transactions on
Image Processing
, Vol. 9, No. 7, pp 1158-1170.
Vargic, R., 1998. An approach to 2D wavelet transform
and its use for image compression.
Radioengineering,
Vol. 7, No. 4, 1-6.
Vetterli, M., and Kovacevic, J., 1995. Wavelets and
Subband Coding,
Englewood Cliffs, NJ, Prentice Hall.
Yang, S.H., and Cheng, T.C., 2000. Error-resilient SPIHT
image coding. Electron. Lett., vol.36, no. 3, pp. 208-
210.
Ye, S., Sun, Q., and Chang, E., 2004. Edge directed filter
based error concealment for wavelet-based images.
Proceedings of International Conference on Image
Processing
(ICIP '04), Singapore, Vol. 2, pp 809- 812.
REAL-TIME IMAGE WAVELET CODING FOR LOW BIT RATE TRANSMISSION
163
