DIRECTION BIASED SEARCH ALGORITHMS FOR FAST

BLOCK MOTION ESTIMATION

Niranjan Mulay

Sasken Communication Technologies Ltd, Products Division, India

Keywords: Video compression, fast motion estimation, block matching, direction biased search patterns.

Abstract: Motion estimation (ME) is computationally the most challenging part of the video encoding process. It has a

direct impact on speed and qualitative performance of the encoder. Consequently, many sub-optimal but

faster ME algorithms have been developed till date. In particular, the Three Step Search (TSS) and Four

Step Search (FSS) algorithms have become popular because of their ease of implementation. The TSS

algorithm is a uniformly spaced block matching algorithm, which performs better in case of large motion.

On the other hand, the New Three Step Search (NTSS) and FSS are center-biased algorithms that

outperform TSS in case of smooth correlated motion. Later, another center-biased search technique namely,

the Diamond Search (DS) algorithm was introduced which was proved to deliver a faster convergence than

FSS in case of smooth motion scenarios. However, the performance of the center-biased algorithms

degrades in sequences having consistently large or uncorrelated motion as they become susceptible to

getting trapped in local minima near the center. In this paper, two novel ME algorithms, namely, dual square

search (DSS) and dual diamond search (DDS) are proposed in order to strike a balance between the center-

biased and uniformly spaced search techniques. The proposed algorithms suggest that a decision to shift the

search center should be delayed till the candidates on a coarse as well as fine grid are evaluated. Moreover,

these algorithms are modeled to exploit motion vector distribution found in most of the real world video

sequences by giving more precedence to candidates near the center, followed by the candidates in the

horizontal and vertical directions than those in the diagonal direction. The performance of the proposed

algorithms is compared with TSS and FSS algorithms in terms of computational speed, motion

compensation error and the compression achieved for various kinds of video sequences. The tested

sequences show that both these algorithms can be substantially faster than TSS and FSS. The proposed ME

algorithms promise to achieve a balanced tradeoff amongst ‘speed - bit rate - quality’ for different kinds of

motion sequences.

1 INTRODUCTION

The main objective of the Motion Estimation (ME)

module is to exploit the temporal redundancy

between successive frames of a video sequence in

order to reduce the number of bits required for

coding. In this paper, we focus on the block

matching ME algorithms. In these block based

coding schemes, the moving regions across the

frames are analyzed by subdividing the frames into

smaller units called blocks. The video standards

such as H.26x and MPEG series (H263, 1998;

MPEG4, 1999) specify block based coding

techniques. The block based ME algorithms try to

find the best matching block, the one giving the least

Block Distortion Measure (BDM), in the reference

frame for every block in the current frame. The idea

is to encode the error data between the current block

and the best matching block along with its

displacement. The displacement is known as the

motion vector (MV). The range of motion vectors is

generally restricted to the certain region specified by

the standard. This region is also known as search

window. Most of the fast ME algorithms work under

the assumption that the error surface is monotonic.

The term error surface indicates a surface defined by

the block distortion measured between the current

block and every candidate block in the search

window of a reference frame. The error surface is

monotonic if there is a distinct trough at the global

minimum and it increases monotonically as the

checking point moves away from the global

140

Mulay N. (2006).

DIRECTION BIASED SEARCH ALGORITHMS FOR FAST BLOCK MOTION ESTIMATION.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 140-148

DOI: 10.5220/0001570201400148

 SciTePress

minimum. But for most of the real video

applications or fast motion sequences, the error

surface may not be always monotonic. Instead there

could be multiple local minima in the search area.

However, the assumption of monotonic surface

facilitates the development of search patterns and

hence most of the fast ME algorithms are developed

under this assumption. The FS algorithm does an

exhaustive search and evaluates each and every

candidate in the search window to reach at the

candidate with minimum BDM that may be called as

the global minimum for that current block.

Let [-W, +W] be the maximum range allowed for

motion vectors in horizontal and vertical direction

[i.e. search window size = (2W+1)]. We have done

the comparative analysis for some of the popular

ME algorithms for W = 7, i.e. for search area of 15 x

15 pixels around the center. The FS algorithm does

an exhaustive search demanding (2W+1)

= 225

BDM computations per block. Hence, various sub-

optimal and fast ME algorithms are developed in an

attempt to devise a mechanism of choosing the

suitable subset of these 225 candidates. The TSS

algorithm starts with the 8 search points at large step

size, typically half the search range. At every stage,

the search center is moved to the best match in the

previous step and the stepsize is reduced by half.

Therefore, TSS always demands fixed 25 search

points to trace any point within W = 7 window. For

most of the real world video sequences, the motion

vector distribution is observed to be prominently

biased towards the zero motion. The various center-

biased algorithms such as NTSS (Zeng et al., 1994,

pp.438-442), FSS (Po and Ma, 1996, pp.313-317)

and DS (Tham et al., 1996, pp.369-377) were

developed to exploit this fact in order to efficiently

detect small motions appearing in stationary or

quasi-stationary (within a region of +/- 2 pixels)

blocks. As compared to TSS, the NTSS algorithm

ensures the fast detection of quasi-stationary blocks

by using a half way stop technique. However, NTSS

demands worst case 33 search points for large

motion blocks, 8 more than TSS. The FSS algorithm

is a center-biased algorithm as it typically starts on a

fine grid of step size 2. The center-biased strategy of

FSS makes it far more efficient than NTSS while

providing the same quality as that of NTSS. Later,

another center-biased algorithm, namely, the

diamond search [DS] was proposed to speed up the

motion estimation of stationary and quasi-stationary

blocks. Even though, both the algorithms - FSS and

DS, perform their best for slow motion sequences,

DS is proved to be faster in terms of required

number of search points. However, the work done

by Tham et al. (1996) mentions that FSS can be

more efficient than DS beyond +/- 3 region.

Moreover, this best-case analysis assumes that the

error surface is monotonic. But in practice, FSS and

DS might take larger number of block comparisons

than the best possible theoretical numbers. In

general, it is observed that the performance of

center-biased algorithms degrades as compared to

that of TSS if the majority of motion vectors lie

beyond +/- 3 region. With these observations

mentioned here and with the due consideration to the

space constraints, we have limited the comparison of

the proposed algorithms in our simulation

experiments to TSS and FSS algorithms.

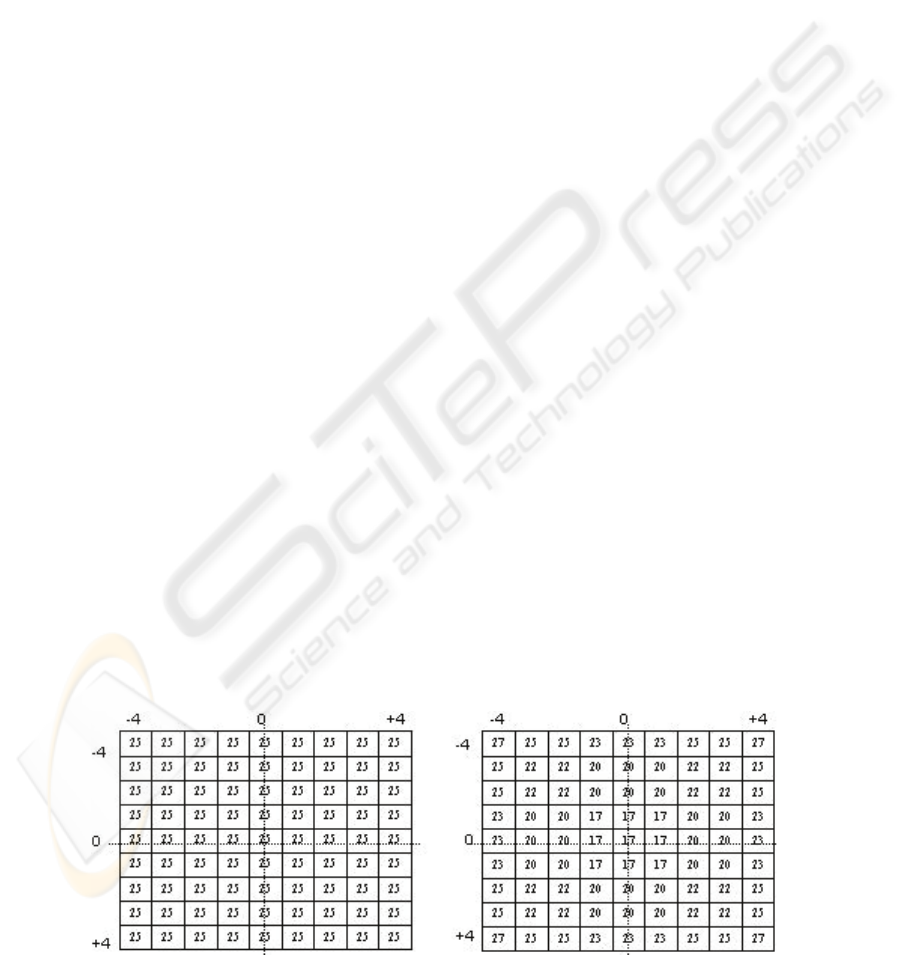
The figure 1 illustrates the best-case number of

search points required to be evaluated for TSS and

FSS algorithms in order to converge at a particular

location. The comparative numbers are shown only

for the motion vectors restricted within a region of

+/- 4 pixels around the center [i.e. |MV| <= 4

region]. As mentioned earlier, for the given window

size W = 7, TSS always requires fixed 25 number of

search points to trace any location. In case of FSS,

the number of search points required to reach at a

particular location varies with its distance from the

center. Compared to TSS, FSS is faster for near

center locations, but the number of block

comparisons required increases with the increase in

(a) TSS (b) FSS

Figure 1: Best-case analysis for TSS and FSS.

DIRECTION BIASED SEARCH ALGORITHMS FOR FAST BLOCK MOTION ESTIMATION

141

distance from the center. It can be perceived that

within |MV| <= 4 region, FSS outperforms TSS but

beyond that, TSS is the clear winner.

The best-case analysis of the above-mentioned

popular algorithms helps to evaluate the

performance of the proposed algorithms. This paper

is organized as follows. In section 2 of the paper,

two ME algorithms are proposed and their

performance is theoretically analyzed in terms of

computational requirement. The section 3 presents

the simulation results in order to evaluate the

performance of the proposed ME algorithms in

comparison with TSS and FSS. The conclusions are

drawn in section 4.

2 ME ALGORITHMS

As discussed earlier, the TSS is a coarse to fine

search algorithm that performs better in cases where

the best match is located far from the center whereas

FSS and DS are center-biased search algorithms

which yields faster convergence when the best

match

is located near the center of the search. For

the sequences having consistent large or

uncorrelated motion, the center-biased algorithms

might maintain faster convergence than TSS but

they seem to get trapped in nearby local minima,

thereby giving a high speed but poor compression,

affecting the quality (Alkanhal et al., 1999).

The interesting observation in TSS, FSS and DS

algorithms is that the center is immediately moved

after all the candidates at the same step size (might

be coarse or fine)

gets evaluated in stage1. This is

critical to these algorithms as they can get trapped in

local minima (Turaga and Chen, 2001). To minimize

this intricacy, the proposed algorithms suggest that a

decision to shift the search center should be delayed

till the candidates on a coarse as well as fine grid are

evaluated. This makes the proposed algorithms more

robust giving a better starting point for the

succeeding stage and hence promises to enhance the

chances of reaching global minima quickly. The

work presented by Cheung and Po (2002, pp.1168-

1177) mentions that the majority percentage of

motion vectors are typically enclosed within the

central 5x5 area, i.e. a region of +/-2 pixels around

the zero motion position. Also it is known that even

though the block displacement of real world video

sequences can be in any direction, the motion is

predominant in the horizontal or vertical direction.

The algorithms proposed in this section exploit these

two facts giving less priority to candidates in a

diagonal direction. The proposed algorithms can

trace the maximum motion displacement of +/- 7

pixels (i.e. W=7).

2.1 Algorithm I: Dual Square

As the probability of finding the best match within

an area of +/-2 pixels around the zero motion vector

is very high, the number of search points required to

converge at these points becomes an important issue.

Hence, the proposed algorithm aims to maintain the

advantage of the center-biased algorithms by

ensuring fast convergence within this area. The basic

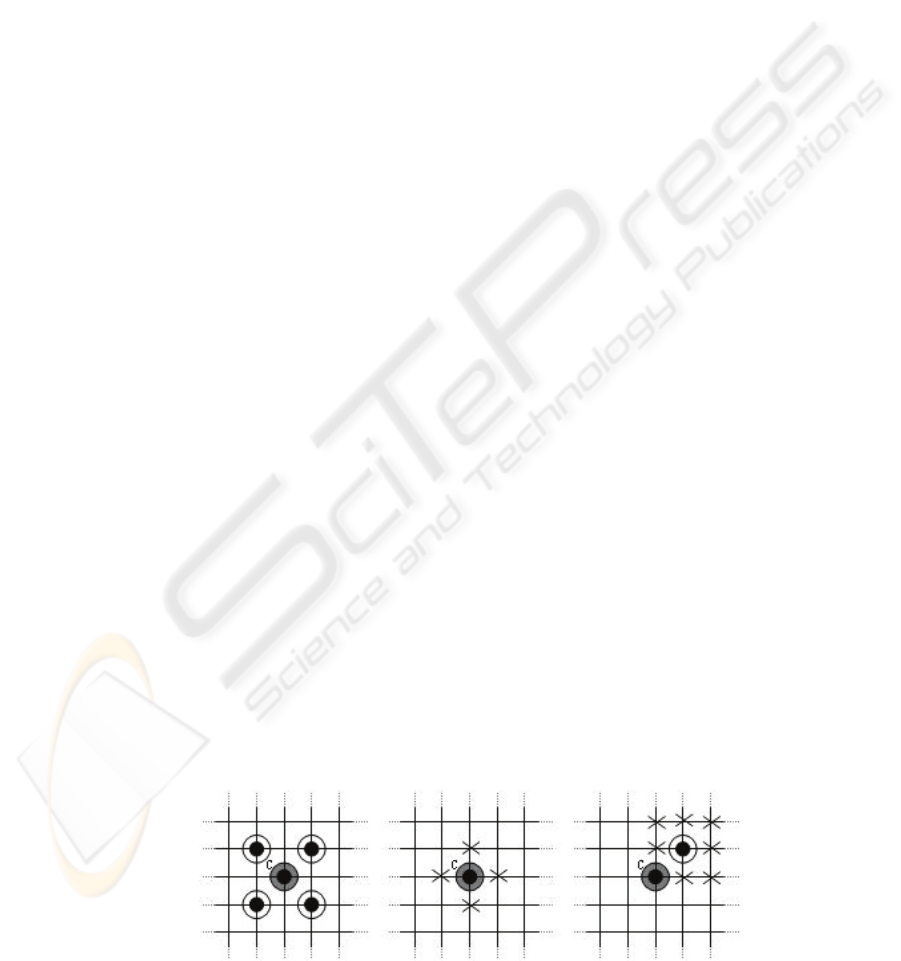
square search configuration used in dual square

search (DSS) algorithm is indicated in figure 2. This

configuration is used to localize the search within

5x5 window (or +/2 region) of the selected center.

Let, ‘C’ be the block in a current frame whose

best match is to be found in the reference frame. The

figure 3 indicates the candidates from a reference

frame chosen for searching the best match. The

algorithm involves two square shaped patterns, a

short square at step size 1 and a long square at step

size 5. The algorithm starts with BDM calculation of

5 candidates in step 1 using basic square search

configuration at the center. If the minimum BDM

point is found at the center, only 4 additional block

comparisons are needed to stop the search. If the

minimum BDM point is found on the short square

then the center is not immediately moved to this

point. The key is to evaluate 4 candidates on a

distant grid, 2 in horizontal direction and 2 in

( a ) b ) ( c )

Figure 2: (a) Basic square search configuration. (b) Next step if center is the best match. (c) Next step if the candidate of a

square is the best match.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

142

L: Long Square S: Short Square

Figure 3: Dual Square Search.

vertical direction and only then take a decision to

move the center of the search in a direction of the

best match. This is the center corrective step to make

the algorithm more robust minimizing the chances of

being trapped in local minima. The further

convergence path will be clearer with the following

explanatory steps.

Step 1: Use basic square search to evaluate 4

candidates of a short square along with the co-

located block. If the center C is the point of

minimum BDM, evaluate just 4 candidates on a ‘+’

sign of stepsize 1 and the best match amongst these

candidates will be the final integer motion vector.

Step 2: If the best match in step 1 is found at the

short square candidate, evaluate L2, L4, L6 and L8

as a center corrective measure. Even after these

comparisons, the short square candidate is proved to

be the minimum BDM point then move the center to

this point for the next stage and calculate the block

distortion for the 7 valid points of a square of

stepsize one around this newly shifted center to find

the final best match candidate.

Step 3: If step 2 delivers minimum BDM at one of

the long square candidates (amongst L2, L4, L6,

L8), then evaluate two points in a diagonal direction

lying in the relevant zone of the motion field. For

e.g. if step 2 yields L2 as the best match, then

evaluate L1, L3 and only then take a decision to shift

the search center. Once the center is shifted to the

minimum BDM point, the final best match is found

out by doing a basic square search at that point.

From the algorithm, it can be perceived that the

search technique uses two-tier strategy each time

before shifting the center. It tries to exploit the

features of both, the center-biased and non center-

biased search algorithms.

Computational Complexity:

With the DSS algorithm, any candidate within 15 x

15 window is traceable. The total number of search

points is varied from (5 + 4) = 9 in the best-case to

(5+4+2+4+7) = 22 in the worst case. The figure 4

depicts the number of search points required to reach

a particular location within |MV| <= 4 area.

Figure: 4 Best-case analysis for DSS.

It can be clearly seen that the algorithm promises

faster convergence than TSS and FSS to converge at

any point within W=7 region. The ability to detect

stationary and quasi-stationary blocks with just 9 or

16 search points and to detect large motion blocks

with maximum of 22 search points makes DSS a far

more efficient algorithm than the previous search

techniques.

2.2 Algorithm II: Dual Diamond

As mentioned earlier, the motion in real video

scenarios is predominant in the vertical and

horizontal directions. The fact that the motion in the

diagonal direction is very rare is evident by the

‘probability matrix of MV distribution’ presented in

the work of Cheung and Po (2002). This fact has

inspired the direction biased – dual diamond search

(DDS) algorithm to achieve faster convergence

along the horizontal and vertical directions at the

expense of higher computational cost to converge in

the diagonal direction. The search pattern of the

proposed algorithm involves a combination of both

the techniques, center-biased as well as uniformly

spaced search technique. The algorithm still

maintains the two-tier strategy to evaluate

candidates on finer as well as coarser grid before

shifting the search center.

DIRECTION BIASED SEARCH ALGORITHMS FOR FAST BLOCK MOTION ESTIMATION

143

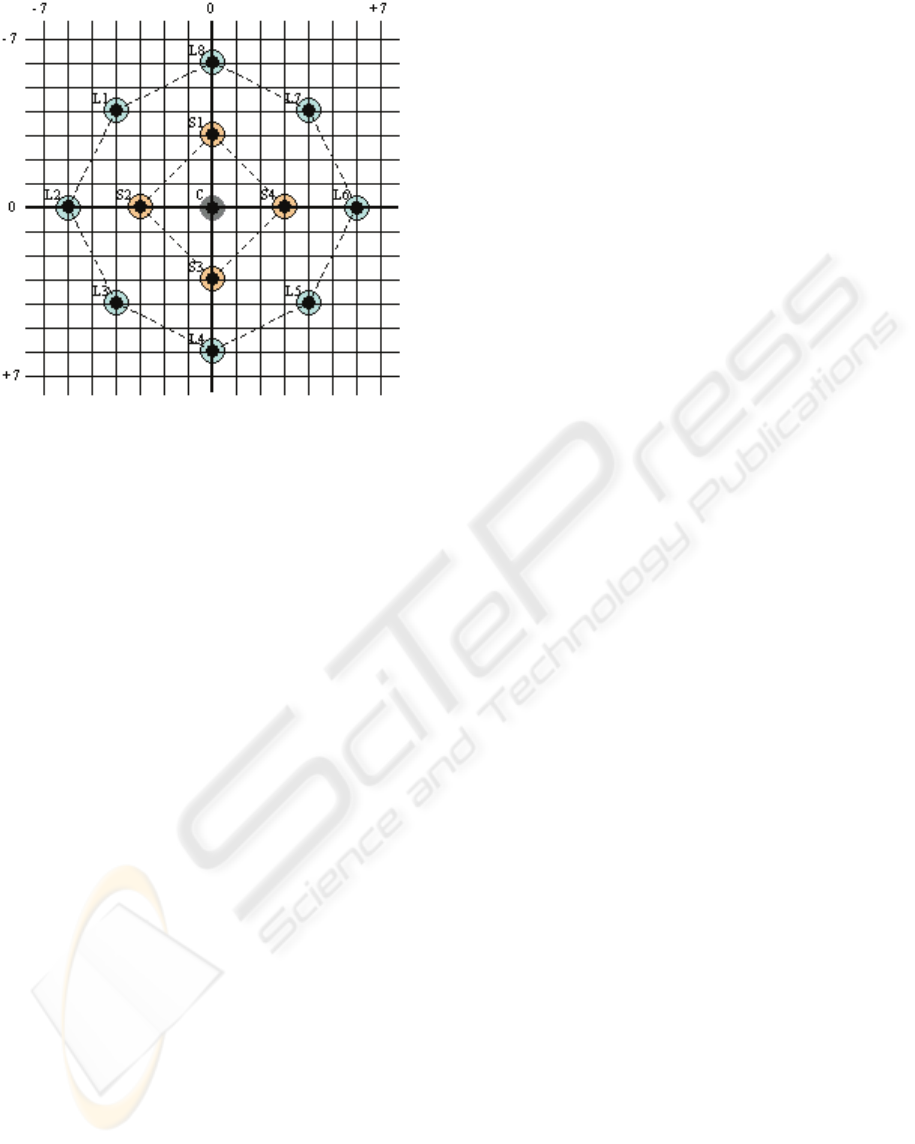
S : Short Diamond L : Long Diamond

Figure 5: Dual Diamond Search.

The search pattern used in the DDS algorithm

involves two shapes: small diamond shaped pattern

and long diamond shaped pattern. In true sense, the

outer shape is octagonal, but it will be referred as a

long diamond in this text. In the very first step, the

DDS algorithm evaluates 4 candidates of a short

diamond at stepsize 3 along with the co-located

block. If the center C is the best match, evaluate 8

candidates of a square of stepsize 1 around the

center. The minimum BDM point will indicate the

final integer MV. Let this process of evaluating 8

candidates of a square of stepsize 1 around the

selected center be designated as ‘short square

search’. If step 1 yields the best match on the short

diamond then take a center corrective step like in

DSS to evaluate 4 candidates on a distant grid,

namely, L2, L6 in the horizontal direction and L4,

L8 in the vertical direction. If a short diamond point

still holds to be the point of minimum BDM, move

the search center at this point and do a short square

search to find the final best match. Otherwise if the

minimum BDM point is found on the long diamond

then evaluate the two diagonal candidates in the

probable zone of the motion field. If the best match

is amongst L2, L4, L6 and L8 then the final best

candidate is traced by a short square search

technique at that point. In case of the minimum

BDM point being found in a diagonal direction, a

technique similar to TSS is employed to search the

best matching candidate. The DDS algorithm is

summarized as follows.

Step 1: Compute block distortion for co-located

block and 4 candidates of a short diamond. If the

center C is the point of minimum BDM, apply short

square search technique at the center to find the final

integer motion vector.

Step 2: If the best match in step 1 is amongst the

short diamond candidates, evaluate L2, L4, L6 and

L8 as a center corrective measure. After these

comparisons, if the short diamond candidate is

proved to be the point of minimum BDM then the

decision to move the search center to this point is

taken. This shift of a search center is then followed

by a short square search to find the final best match

candidate.

Step 3: If step 2 delivers minimum BDM at one of

the long diamond candidates (amongst L2, L4, L6,

L8), then evaluate two points in a diagonal direction

lying in the relevant zone of a motion field. For e.g.

if step 2 yields L8 as the best match, then evaluate

L1, L7 and only then take a decision to shift the

search center. After evaluation of two relevant

diagonal candidates, if minimum BDM point is still

found at the previously shortlisted horizontal/vertical

candidate then the center of the search is shifted to

this point. The final best match is found out by doing

a short square search at that point.

Step 4: If the diagonal candidate proves to be the

best match in step 3 then the center is moved to this

point and a search pattern similar to TSS is

employed to finalize the integer MV. Here, 8

candidates at a stepsize of 2 from the center are

evaluated and in the next step, center is moved to the

minimum BDM point and step size is halved to 1. In

the last step, 8 candidates around this new center are

evaluated to deliver the final MV location.

From the above explanations, it is apparent that

the algorithm is well modeled to exploit the

probability distribution of motion vectors. The

details about the probability distribution of motion

vectors can be found in the work of Cheung and Po

(2002). The DDS algorithm is direction biased as it

gives the highest preference to the candidates near

zero motion location followed by the candidates in

the horizontal and vertical directions. The algorithm

takes longer time to converge in a diagonal

direction, as the motion in this direction is rare in

practical scenarios. Like DSS, the DDS algorithm

attempts to combine the features of both the center-

biased and uniformly spaced search strategies. The

center corrective approach in DDS helps to maintain

the robustness by minimizing the chances of getting

seized in the local minima. Unlike DSS, DDS speeds

up the motion estimation of blocks moving largely

in the horizontal and vertical directions. This might

be crucial for the CIF sequences compared to QCIF

sequences as the CIF sequences typically manifests

larger motion due to scale up effect.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

144

Computational Complexity:

The DDS algorithm can trace any candidate within

15x15 search window. The total number of search

points in the best-case are (5 + 8) = 13. The DDS

algorithm exhibits a noticeable faster convergence

along the horizontal and vertical directions by

demanding maximum of 17 BDM computations for

|MV| <= 4 and 19 BDM computations for |MV| > 4.

However, if the best match lies in a diagonal

direction then the algorithm

demands worst case 27

search points, two more than TSS. The fig. 6 depicts

the number of search points required to reach a

particular location within |MV| <= 4 area.

Figure 6: Best-case analysis for DDS.

The analysis shown in fig. 6 indicates that the

DDS algorithm exploits the MV distribution found

in the real world sequences. For the blocks having

motion within +/- 1 region, the DDS algorithm

performance is better than that of TSS, NTSS, FSS

and more or less the same (if not better) as that of

DS. The point to be noted is that any candidate in

horizontal and vertical direction beyond +/- 1 region

can be traced with just 17 or 19 BDM computations.

The algorithm is more efficient than other

algorithms in case the best match consistently lies in

near center region or in the horizontal/vertical

direction. Nevertheless, the 27 BDM computations

required to reach a location in the diagonal direction

seems like an expensive penalty. But given the fact

that it is very unlikely to find consistent motion in a

diagonal direction for real world scenarios, the DDS

algorithm maintains its performance across various

kinds of motion sequences.

3 EXPERIMENTAL RESULTS

We have summarized the results of our simulation

experiments in this section. The algorithms have

been analyzed in MPEG4 framework for a large

number of QCIF/CIF test sequences. However, with

due regards to the space limitations, the results are

tabulated only for five CIF sequences representing

different types of motion content. These are the

YUV420 sequences captured at 15 fps. The

algorithms have been analyzed for the block size, N

= 16 and search window, W = 7. The error measure

namely, ‘Sum of absolute difference’ (SAD) is used

as a BDM for a block matching criterion. For block

size = N, One SAD computation demands [2N

Load, N

Sub, N

Abs, (N

- 1) Add] operations. The

tools like - unrestricted motion vectors and

macroblock skipping are disabled.

The performance is analyzed based on the

following three parameters:

1. Speed: Average number of search points per

block.

2. Quality: The quality of the motion estimation is

analyzed in terms of mean square error (MSE)

between the original frames and the motion

estimated frames.

3. Compression: The number of bits required to

code a particular sequence conveys practically

the most significant information. This is

analyzed in terms of the average number of bits

required per block. The rate control module is

disabled, rather kept as VBR (variable bit-rate)

in order to see the direct impact of motion

estimation algorithms on the size of the bit

streams.

From the table 1, it can be seen that for the low

motion sequences like Akiyo and Hall, all the

algorithms perform equally good in terms of quality

and compression. However, in terms of speed, DSS

clearly out-shadows the other algorithms, as it

demands nearly half the BDM computations as

compared to that of FSS. For the selected sequences,

FSS is observed to be always faster than the TSS

algorithm. However, when compared for the

sequences with greater motion content like

coastguard, foreman, and football the FSS fails to

find good matches and thereby it shows degradation

in terms of MSE and the number of bits needed. For

these fast motion sequences, the DSS algorithm

maintains its significant speed efficiency at the cost

of some more quality degradation compared to that

of FSS. This is where the DDS algorithm

outperforms the other algorithms by exhibiting a

good ‘speed-quality’ tradeoff. Compared to DSS, the

DDS algorithm takes slightly more number of search

points, still less than FSS and tries to achieve the

qualitative solution as close as that of TSS. Most of

the center-biased algorithms show considerable

degradation in their performance for large motion

sequences. Our simulation results show that, DDS

can offer a better solution to counteract this problem

common to most of the center-biased algorithms.

DIRECTION BIASED SEARCH ALGORITHMS FOR FAST BLOCK MOTION ESTIMATION

145

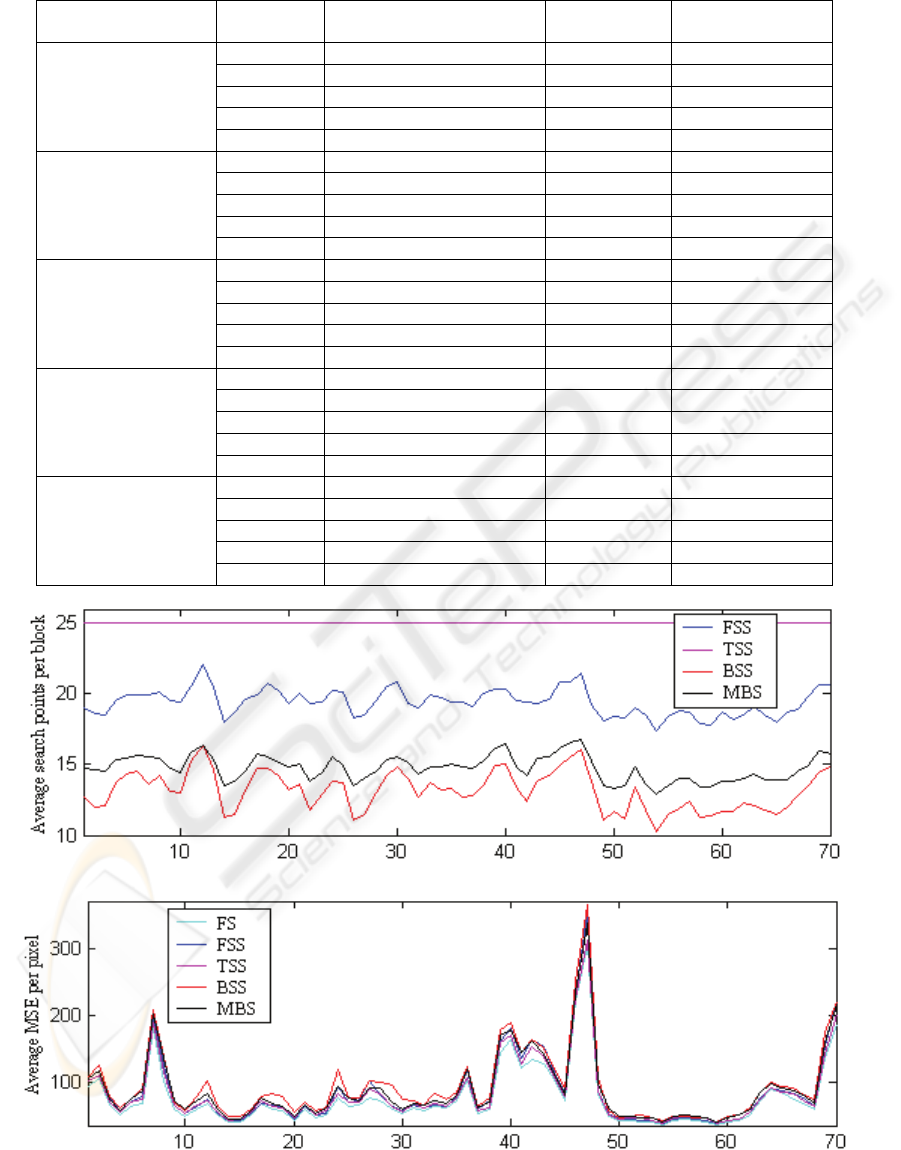
Table 1: Performance Analysis for CIF Test cases.

Test

Sequence

Algorithm Avg. no. of search points

per block.

Average MSE Average number

of bits per block

FS 225 19.64 14.547

TSS 25 19.92 14.485

FSS 15.86 19.9 14.458

DSS 8.51 20.11 14.413

Akiyo

[Slow motion]

DDS 12.22 20.03 14.512

FS 225 42.69 36.495

TSS 25 43.36 35.151

FSS 16.02 44.09 35.062

DSS 8.68 45.33 35.000

Hall

[Moderate &

correlated motion]

DDS 12.39 43.84 35.268

FS 225 129.95 154.738

TSS 25 138.68 160.515

FSS 18.94 148.95 166.596

DSS 11.2 163.92 186.681

Coastguard

[Large &

correlated motion]

DDS 14.98 138.07 160.105

FS 225 222.05 123.412

TSS 25 230.94 126.467

FSS 19.53 243.08 129.055

DSS 13.72 252.43 131.806

Foreman

[Moderate &

uncorrelated motion]

DDS 15.39 240.88 127.503

FS 225 335.67 209.184

TSS 25 353.58 216.811

FSS 20.76 385.58 229.513

DSS 15.36 393.5 231.831

Football

[Fast Motion]

DDS 17.15 377.7 220.6

Frame Number

(a)

Frame Number

(b)

Figure 7: Comparison of TSS, FSS, DSS and DDS in terms of average search points and MSE for the foreman sequence.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

146

It can be seen that, especially for the fast motion

sequences, the performance of DDS algorithm is

better than FSS with regards to all the three

parameters - speed, quality and compression.

The figure 7 shows the performance of each of

the search techniques for the foreman sequence on a

frame-by-frame basis. The foreman sequence is

selected because it has some fast, uncorrelated

motion and it doesn’t favor center-biased or non-

center-biased search pattern in particular. It can be

seen that the DSS algorithm substantially improves

the speed efficiency at the cost of marginal increase

in the distortion. Thus, the DSS can be justified as

the natural choice for many time critical

applications. Otherwise, DDS gives an option of

trading off some speed compared to DSS for the

improvement in quality.

4 CONCLUSIONS

The two sub-optimal block matching algorithms,

namely, Dual Square Search (DSS) and Dual

Diamond Search (DDS) are proposed in this paper.

The number of search points required to trace a

particular position varies depending on the direction

of the position with respect to the center. The

algorithms give the highest preference to the

candidates near the center and the least preference to

the candidates in the diagonal direction. Both the

algorithms are based on the principle that the

candidates on a finer grid and those on a coarser grid

should be evaluated before taking a decision to

move the search center. This center corrective

approach makes these algorithms more robust

minimizing the chances of getting trapped in local

minima. The DDS algorithm goes one step further to

model its search strategy in order to exploit the MV

distribution of most of the real world video

sequences. With regards to the computational speed,

both the proposed algorithms, DSS and DDS clearly

outperform TSS and FSS algorithms. For large or

uncorrelated motion sequences, DSS may suffer

from more degradation in terms of quality.

Nevertheless, DSS enjoys the privilege of being the

fastest algorithm amongst these algorithms. Between

the two proposed algorithms, DSS is more effective

than DDS algorithm for smooth and small motion

sequences thereby promising to work at its best in

videoconference kind of applications. Moreover, the

DSS algorithm possesses the features like regularity

and simplicity that might be helpful for hardware

implementations. However, DDS is the one that

combines the efficient center-biased nature of FSS

with the advantage of TSS to find good matches for

large motion sequences. Compared to DSS, the DDS

algorithm has an ability to tradeoff some speed in

order to maintain its performance in terms of quality

and compression regardless of the motion content.

Clearly, the proposed algorithms try to blend the

best features of the center-biased and uniform search

strategies so as to provide good performance in

terms of ‘speed-quality-bit rate tradeoff’ when

considered across different kinds of motion

sequences including panning, zooming, smooth,

correlated, uncorrelated and fast motions.

REFERENCES

ITU-T Recommendation H.263, 1998. ‘Video coding for

low bit rate communication’.

ISO/IEC 14496-2 (MPEG4 visual), 1999. ‘Information

technology – Coding of audio-visual objects - Part

2:Visual’.

Turaga, D. and Chen, T. 2001. ‘Estimation and mode

decision for spatially correlated motion sequences’,

Technical Report AMP 01-01, Electrical and

Computer Engineering, Carnegie Mellon University,

Pittsburgh.

Rao, A. and Raghavan, M. 2003. ‘Fast motion estimation

algorithms computation and performance trade-offs’.

Zeng, B., Liou, M. and Li, R. 1994. ‘A new three step

search algorithm for block motion estimation’, IEEE

Trans. Circuits Syst. Video Technol., vol. 4, pp. 438-

442.

Po, L. and Ma, W. 1996. ‘A novel four step search

algorithm for fast block motion estimation’, IEEE

Trans. Circuits Syst. Video Technol., vol. 6, pp. 313-

317.

Tham, J. et al. 1996. ‘A novel unrestricted center-biased

search algorithm for four step search algorithm for fast

block motion estimation’, IEEE Trans. Circuits Syst.

Video Technol., vol. 8 (no. 4), pp. 369-377.

Alkanhal, M., Turaga, D. and Chen, T. 1999, ‘Correlation

based search algorithm for motion estimation’.

Cheung, C. and Po, L. 2002. ‘A novel cross diamond

search algorithm for fast block matching motion

estimation’, IEEE Trans. Circuits Syst. Video

Technol., vol. 12 (no. 12), pp. 1168-1177, Dec 2002.

DIRECTION BIASED SEARCH ALGORITHMS FOR FAST BLOCK MOTION ESTIMATION

147