SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE

TRANSFORMS

Susanna Minasyan, Karen Egiazarian, Jaakko Astola

Tampere University of Technology, Tampere, Finland,

David Guevorkian

Nokia Research Centery,Tampere,Finland

Keywords: Signal denoising, Wavelet, Threshold, Parametric transform.

Abstract: Orthogonal transforms have found considerable interest in signal denoising applications. Recently

Parametric Haar-like Transforms (PHTs) have been introduced and shown to be efficient in image denoising

and compression applications. PHT is such that it may be computed with fast algorithm in structure a

similar to that of classical fast Haar transform and such that its matrix contains a predefined basis vector,

called generating vector, as its first row. PHT may be adapted to the characteristics of the input signal or to

its parts by a proper selection of the generating vectors. Possibility of adaptation to the input signal may, in

principle, be significant source for performance improvement of transform based signal processing

algorithms. In this paper, the capability of parametric Haar-like transforms, in 1-D signal denoising

application is explored. A new PHT based post-processing algorithm for 1-D signal denoising is proposed,

which may be combined with another denoising method in order to improve the quality of the output signal.

Experiments were conducted where the basic wavelet thresholding based signal denoising method was

complemented with the proposed post-processing algorithm. Simulation results illustrate significant

performance improvement due to the use of the proposed algorithm.

1 INTRODUCTION

One of the most important problems in signal

analysis is noise suppression or denoising where the

problem is to find an estimate of a signal that was

corrupted by a noise, e.g. additive Gaussian noise.

Conventional denoising methods, in particular,

Wiener filtering, are based on linear methods. Non-

linear methods such as filtering in wavelet transform

domain or wavelet-thresholding introduced by

Donoho and Johnstone (Donoho et al, 1994),

(Donoho, 1995), have also been shown be very

efficient in signal denoising. Mostly, wavelet

denoising was focused on statistical modeling of

wavelet coefficients and optimal choice of threshold

values (Grace Chang et al, 2000). In practice, the

most commonly applicable are soft and hard

thresholding functions. Recently, another function

called customized thresholding was proposed (Yoon

et al, 2004) that depends on a set of parameters and

can be adapted to the input signal. The customized

thresholding function combines advantages of

traditional soft and hard thresholding, it can become

either one of them by setting parameter values. The

idea of customized thresholding is similar to that of

semi-soft or firm shrinkage (Gao, 1996) and the non-

negative garrote thresholding function (Gao, 1998).

It was shown that custom thresholding function

outperforms the traditional ones and it improves

denoising results significantly.

Besides wavelets, different other orthogonal

transforms (Egiazarian et al, 1999, Pogossova et al,

2003, Oktem et al, 1999) such as Fourier and DCT,

Haar, combination of DCT and Haar, Tree-

Structured Haar Transforms (THT), Generalized

Lapped transforms and others have been proposed as

useful tools in signal denoising applications. In

many cases local transform based denoising methods

are more profitable than wavelet based denoising

methods which are applied to the whole signal.

134

Minasyan S., Egiazarian K., Astola J. and Guevorkian D. (2006).

SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 134-139

DOI: 10.5220/0001570401340139

 SciTePress

Recently there has been considerable interest in

constructing signal adapted systems for signal

denoising, compression, and other applications

(Egiazarian et al, 1999, Oktem et al, 1999,

Pogossova et al, 2003). Thereby, parametric

transforms with matrices described in a unified form

involving a set of parameters are of interest

nowadays. In this context parametric transform

means a wide class of discrete orthogonal transforms

(DOTs) that may include classical transforms and an

infinite number of new transforms with the

possibility to select the desired transform according

to parameter values. A unified software/hardware

tool can be used to implement the whole class of

transforms with the possibility to adjust transform

parameters. One can find various methods of

synthesizing the parametric transforms in (Agaian et

al, 1992).

In particular a family of parametric Haar-like

transforms was introduced (Minasyan et al, 2001).

Parametric Haar-like transform (PHT) is such a

DOT that its matrix contains a desired basis function

as its first row and such that it may be computed by

a fast transform algorithm in structure similar to that

of the classical fast Haar transform algorithm.

Efficiency of using PHTs in image compression

(Minasyan et al, 2005) as well as in image denoising

(Minasyan et al, 2006) has motivated a study of their

usefulness also in 1-D signal denoising.

The goal of this paper is to investigate the

potential of PHTs in improving the performance of

signal denoising. A new signal denoising algorithm

is proposed where the corrupted signal is

transformed into the transform domain with PHTs

that are synthesized according to a signal estimate

obtained, e.g. by wavelet denoising. The input noisy

signal and its estimate are split into small sized

windows. For every small window of the estimate

one PHT is synthesized such that its matrix has the

contents of the window as its first row. This PHT is

applied to the corresponding window of the

corrupted noisy signal. Next, the transformed

coefficients are thresholded by customized threshold

(Yoon et al, 2004) and transformed back into the

original domain by the inverse PHT. Simulations

were conducted on several test signals showing

significant improvement in reducing the noise as

compared to the pure wavelet denoising method.

The paper is organized as follows: Section 2

gives a brief introduction to PHT’s. Background on

wavelet thresholding methods is given in Section 3.

Section 4 is the description of the proposed PHT

based denoising algorithm. Section 5 describes

simulations and results of experiments. The

conclusion is given in Section 6.

2 PARAMETRIC HAAR-LIKE

TRANSFORM (PHT)

Orthogonal transforms are widely used in

signal/image processing, in particular, for signal

denoising. In practice, different well-known fixed

transforms with fast algorithms such as Discrete

Fourier, Cosine, Sine, Haar, and Hadamard

transforms are commonly used. Each of these

transforms is suitable for a particular type of input

signals but none of them performs sufficiently well

on different types of input signals. Performance of

fixed transforms, in particular, in signal denoising

may be increased by making use of parametric,

signal adaptive transforms. In a parametric transform

based method different transforms may be

synthesized and applied to different signals or even

to different parts of a signal.

One way of synthesizing parametric transforms

is based on unified representations of fast transform

algorithms (see Agaian et al, 1992), (Minasyan et al,

2001). Such unified representation is based on

factorization of transform matrix of an arbitrary

order N as a product of block-diagonal sparse

matrices and permutation matrices. Blocks of sparse

matrices along with permutation matrices play the

role of synthesis parameters. One can vary these

parameters to synthesize an infinite number of

different transforms all a priori possessing fast

algorithms for their computation. It is also possible

to adjust the parameters to design a transform matrix

having some desired features. Good examples of

synthesising such parametric transforms are the

Haar-like, Hadamard-like transforms which have

been proposed in (Minasyan et al, 2001) where, in

particular, a method was proposed for constructing

an orthogonal Haar-like or Hadamard-like transform

matrix such that its first row is a predefined

normalized vector

,...,

hh h

−

⎡

⎤

⎣

⎦

called generating

vector. In (Minasyan et al, 2001), one can find the

detailed description of constructing a parametric

orthogonal Haar-like transform of order N=2

which involves the generating vector. The transform

matrix has such a structure that its first row

(column) is the generating vector while the rest of

the basis functions are orthogonal to the first row.

And, there is a fast algorithm for every Haar-like

transform implementation similar to that of classical

fast Haar transform algorithm.

SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS

135

It should be noted that the generating vector for

the classical discrete Haar transform of order N=2

is the constant (1x2

)-vector (with all components

equal to each other). Using other generating vectors

of arbitrary length and arbitrary component values

an infinite number of Haar-like transforms, similar

in structure to the Haar transform, may be

synthesized.

Let us consider an example of synthesizing a

Haar-like transform of order N=8 with the

generating vector

()

[]

1 204 1, 2,3, 4,5,6,7,8=⋅h

on its first row. The matrix

of the desired

transform is supposed to be presented as:

(4) (3) (3) (2) (2) (1) (1)

PHPH PH P= ,

where we define

(1) (4)

PP I==

. Then, we define

12 34 5 6

11 1

(1)

21 43 65

561

113

⎡⎤⎡⎤ ⎡⎤

=⊕⊕⊕

⎢⎥⎢⎥ ⎢⎥

−− −

⎣⎦⎣⎦ ⎣⎦

⎡⎤

⊕⋅

⎢⎥

−

⎣⎦

With this matrix we obtain the result of the first

stage:

()

(1)

5, 0,5,0, 61,0, 113,0 .

204

⎡⎤

== ⋅

⎣⎦

We then define the permutation matrix

(2)

(8)

PP= to be the perfect shuffle of order 8.

Applying

)2(

x results in

(2)

(1 204) 5,5, 61, 113, 0,0,0,0 .

⎡⎤

=⋅

⎣⎦

Now we define

)2(

as:

5 5 61 113

(2)

30 174

55 11361

⎡⎤⎡ ⎤

=⊕ ⊕

⎢⎥⎢ ⎥

−−

⎢⎥⎢ ⎥

⎣⎦⎣ ⎦

Applying this matrix to

(2)

yields:

(2) (2)

1 204 30,0, 174,0,0,0,0

⎡

⎤

⎣

⎦

xx .

Taking

(3) ( )

(4)

PP I=⊕ and defining

(3)

30 174

204

174 30

⎡⎤

=⊕

⎢⎥

−

⎢⎥

⎣⎦

we will find

[]

(3) (3)

1, 0,0,0, 0, 0,0,0

HP==

xx .

Substituting the defined matrices into the

factorization of

we obtain the desired matrix:

12345678

2.4 4.8 7.2 9.6 2.1 2.5 2.9 3.3

5.8 11.7 3.5 4.7 0 0 0 0

0 0 0 0 7.4 8.8 5.6 6.4

12.8 6.4 0 0 0 0 0 0

204

0 0 11.4 8.6 0 0 0 0

0 0 0 0 10.9 9.1 0 0

0 0 0 0 0 0 10.7 9.4

≈

⎡

⎤

⎢

⎥

−−−−

⎢

⎥

⎢

⎥

−−

⎢

⎥

−−

⎢

⎥

⋅

⎢

⎥

−

⎢

⎥

−

⎢

⎥

⎢

⎥

−

⎢

⎥

−

⎢

⎥

⎣

⎦

PHT is an input-adapted transform that may be

adjusted to the input signal to improve the

performance of fixed transforms in different

applications. It has recently been shown that PHT

may efficiently be used in image compression

applications (Minasyan et al, 2005) and also in

image denoising (Minasyan et at, 2006). This

motivated us to study the PHT also in signal

denoising.

3 WAVELET THRESHOLDING

FUNCTIONS

Let y=x+z be a (1xN) input noisy signal, x be

corresponding noiseless signal and z be Gaussian

white noise with N(0, σ

Transform–based approach to noise reduction

problem consists of following steps:

1. Transform the noisy signal into the

corresponding transform domain;

2. Apply some thesholding to the resulting

coefficients by zeroing out the coefficients

lower than a certain amplitude;

3. Transform back to the original domain,

performing the inverse transform.

One of the best known denoising methods is

based on using a discrete wavelet transform at Step 1

(and corresponding inverse discrete wavelet

transform at Step 3). The most commonly used

thresholding functions at Step 2 are the hard-

thresholding and soft-thresholding functions.

Recently, the custom thresholding function (CTF)

was introduced .

a) The hard-thresholding function selects

(significant) wavelet coefficients that are greater

than the given threshold λ and sets the others to

zero:

, if λ

()

0, otherwise.

⎧

≥

⎪

⎨

⎪

⎩

(1)

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

136

The hard-thresholding function is discontinuous

at threshold λ, e.g. at |x| = λ. That is why the

artifacts, known as Gibbs phenomena, near the

discontinuities appear in the denoised signal.

b) The soft-thresholding function, which is called

also wavelet shrinkage function, shrinks the wavelet

coefficients by threshold λ towards zero:

λ, if λ

() 0, λ

+λ, if -λ.

−≥

⎧

⎪

⎨

⎪

≤

⎩

(2)

c) The custom-thresholding function, (CTF):

()

()(1 )λ, if | | λ

( ) 0, if

3 4 otherwise(){ () },

sgn

⎧

⎪

−−α ≥

⎪

=≤γ

⎨

⎪

−γ −γ

⎪

αλ α − + − α

⎪

λ−γ λ−γ

⎩

(3)

where γ is the cut-off value, below which the

wavelet coefficients are set to zero, 0< γ < λ , and α

is the parameter that decides the shape of the

thresholding function f

(x), 01.≤α≤ This function

is continuous at λ and can be adapted to the signal

characteristics.The customized thresholding function

may be considered as a linear combination of soft-

thresholding function and hard thresholding function

() () (1 ) ()

ch s

ff f=α⋅ + −α ⋅xx x that is continuous

around the threshold λ. By varying the parameters α,

γ and λ, it is possible to vary the CTF between the

soft and hard thresholding functions or just to switch

from one function to another one.

4 PHT-BASED POST ROCESSING

ALGORITHM FOR SIGNAL

DENOISING

The proposed denoising algorithm belongs to the

general class of transform based denoising

algorithms described in Section 3 where we use the

Parametric Haar-like Transforms (PHT) as the

invertible transform of Step 1 (and its inverse at Step

3). The idea of the proposed algorithm is to use the

signal adapted PHTs instead of fixed orthogonal

transforms in order to better distinguish between

signal and noise in the transform domain. The main

point consists in finding the suitable generating

vectors for PHT synthesis. In an ideal case, if the

generating vectors would be taken from the original

uncorrupted signal, then the whole energy of the

corrupted signal in the transform domain would be

concentrated in only the first transform coefficient.

By zeroing out all the rest coefficients would

remove almost all the noise while would preserve

the original signal untouched. However, since in

reality the original signal is unknown, we may only

use its estimate to form the generating vectors for

PHT synthesis. As such an estimate we use the result

of wavelet denoising. It has been shown that

VisuShrink tends to oversmooth the signal, leading

to loss of details and increase estimation error.

Taking this into account we use the CTF.

The proposed algorithm (Wavelet-PHT

denoising algorithm) may be described in four steps:

1. The input signal is denoised by wavelet

transform to find an estimate of an

uncorrupted signal.

2. The input signal is transferred window by

window (which are non-overlapping) into

the transform domain by PHTs that are

synthesized on the base of the estimate of

the original signal in the corresponding

window obtained at Step 1. Thus, both the

original signal and the estimate are divided

into non-overlapping windows, for

instance, of length 8. For each window of

the estimate the PHT containing the

corresponding window content as its first

row is synthesized. Then, it is applied to the

window of the original signal at the same

location.

3. The customized thresholding is applied to

each transformed window. The parameters

α, λ and γ of the thresholding function were

determined empirically.

4. Then, each thresholded window is

transformed back with inverse PHTs. Note

that the direct and inverse PHTs may be

computed with fast algorithms in structure

similar to that of Haar transform.

5 SIMULATION RESULTS

The proposed method was tested on different

artificial test signals such as Blocks, Bumps,

HeavSine, Doppler, Cusp of length 256 taken from

Matlab’s WaveLab toolbox. The signals were

corrupted by additive Gaussian noise with SNR

(signal-to-noise-ratio) 7 and then denoised by the

proposed algorithm. In all the experiments bellow

the Daubechies asymmetric wavelet with 8

vanishing moments and 8 decomposition levels was

used at Step 1 of the algorithm. The results of the

experiments were averaged over 30 runs.

SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS

137

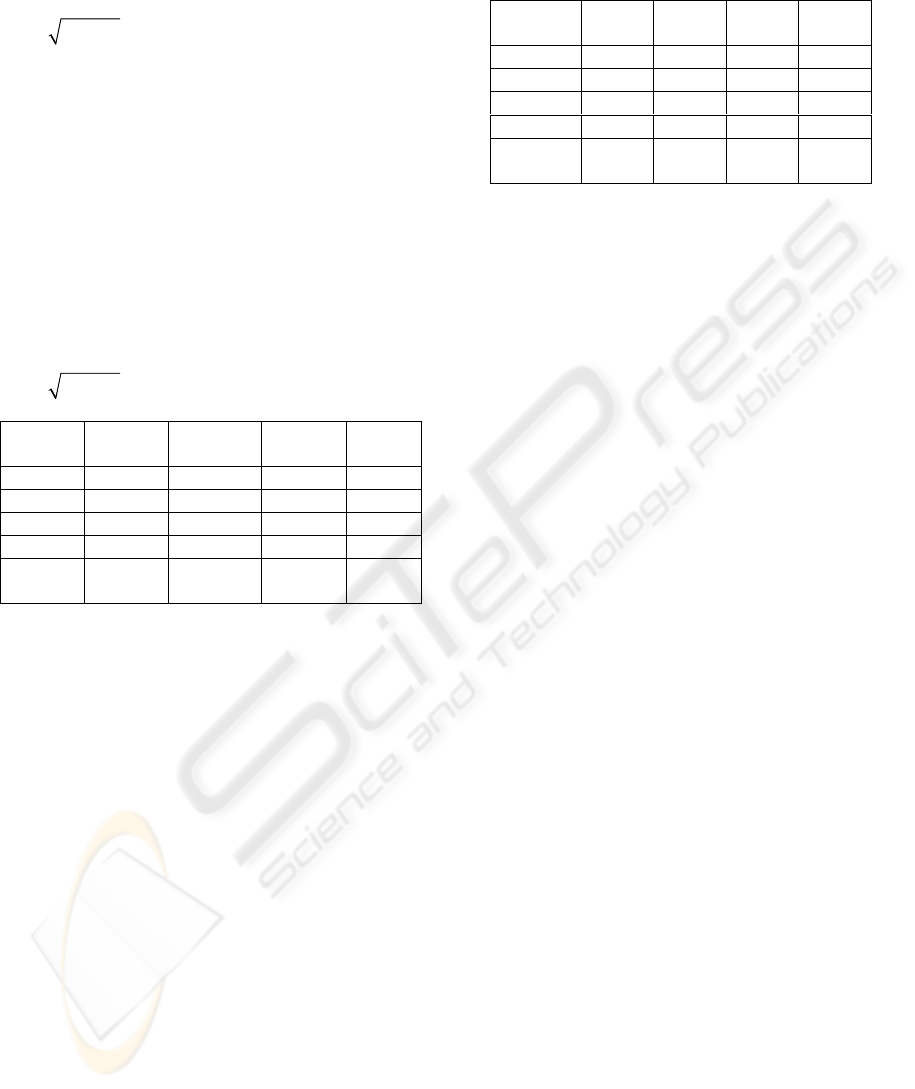
Table 1 presents the results of one set of

experiments. In this experiment soft and hard

threshoding with the universal threshold

2logNλ=σ were used both in wavelet denoising

and in PHT post-processing where N is a length of a

signal in the case of wavelet denoising and N=w=8

is a window size in PHT post-processing. The

second and third columns correspond to soft

thresholding of both wavelet coefficients and PHT

coefficients. The fourth and fifth columns

correspond to the case of hard thresholding. One can

see that in the most of the cases the proposed

method (third column) reduces significantly noise in

the sense of MSE comparing with MSE of soft

thresholded estimate.

Table 1: Comparative results of MSE averaged over 30

runs: denoising with the universal threshold

2logNλ=σ .

Table 2 presents the results of another set of

experiments where the soft and customized

thresholding functions were applied with empirically

optimized thresholding parameters in order to

explore potential of the proposed method.

The second column of Table 2 represents the

MSEw values of wavelet denoising using soft

thresholding with optimized threshold values λ

given in the fourth column of the table

In the third column the values MSEwp obtained

after PHT-based post-denoising are given. Again

window size was chosen w=8 but now CTF with

optimized parameter values

(see column 5), and

fixed

0.97=

and γ =0.9·λ were used (these values

were experimentally found as the optimal for all the

experimented signals).

Table 2: Comparative results of MSE averaged over 30

runs: denoising with empirically found optimal thresholds.

The experiments have shown that for each signal

the optimal ranges of threshold values λ

which

have been used in proposed denoising method for

signals Blocks, Bumps, Doppler, Cusp and

HeaviSine are 4~7.5, 5~7, 2.5~3.5, 3~8 and 3~3.8,

respectively.

Besides, for each signal the confidence intervals

(CI) for MSEwp values were obtained during the

experiments. In particular, CI for Blocks is [0.42,

0.69], CI for Bumps is [0.38, 0.57], CI for Doppler

is [0.32, 0.66], CI for Cusp is [0.13, 0.30] and CE

for HeaviSine is [0.20, 0.53].

It can be seen that by applying the proposed

denoising the remaining noise is reduced

significantly in the sense of MSE.

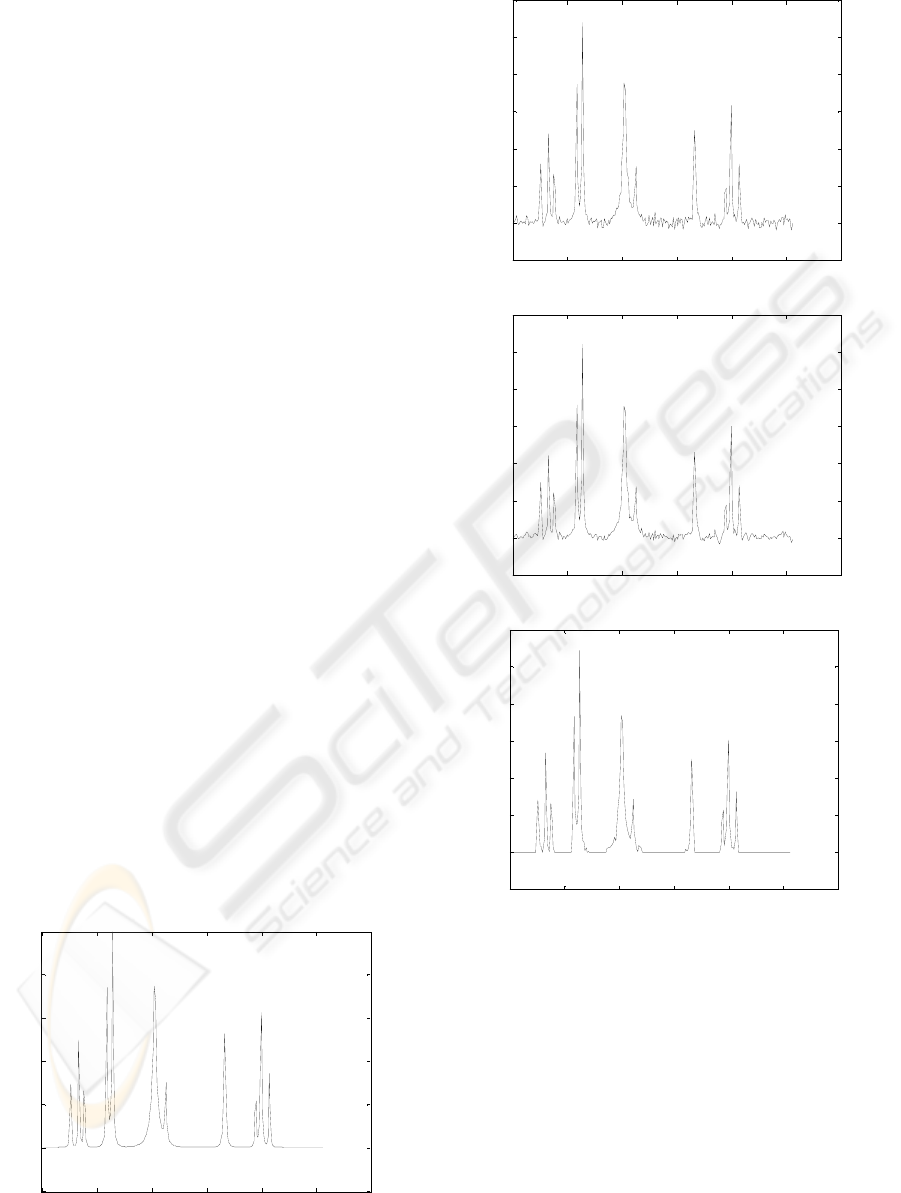
Fig. 1 illustrates the performance of the proposed

algorithm on the example of the signal Bumps. One

can see that the result of the proposed algorithm

(Fig.1,d) is significantly closer to the uncorrupted

signal (Fig.1,a) as compared to the result of the pure

wavelet denoising (Fig.1,c). Performance

improvement is similar for other signals as well.

6 CONCLUSION

A method based on parametric Haar-like transforms

for improving wavelet denoising is presented here. It

employs a parametric Haar-like transform that can

be custom designed for each part (window) of the

signal. The simulation results verify the efficiency of

the proposed method. Similar algorithm may be

extended also to image denoising application.

REFERENCES

Donoho, D.L., and Johnstone, I.M., 1994. Ideal Spatial

Adaptation via wavelet shrinkage, Biometrika.

Donoho, D.L., 1995. De-noising by soft thresholding,

IEEE Transactions on Information Theory.

Signal Soft

PHT

soft

Hard PHT

hard

Blocks 4.18 0.96 1.33 0.82

Bumps 4.62 0.94 1.16 0.76

Doppler 2.34 0.65 0.67 0.63

Cusp 0.70 0.18 0.29 0.39

Heavi

Sine

1.09 0.24 0.35 0.41

Signal MSEw

MSEw

Blocks 0.84 0.57 0.9 6

Bumps 0.81 0.47 0.7 5

Doppler 0.63 0.48 1.3 3

Cusp 0.50 0.19 2.7 7

Heavi

Sine

0.88 0.29 3 3

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

138

Chang, S.G., Yu,B., Vetterli, M., 2000. Adaptive wavelet

thresholding for image denoising and compression,

IEEE Transactions on Image Proccessing.

Yoon, B.-J., Vaidyajnathan, P.P., 2004. Wavelet-based

de-noising by customized thresholding. In ICASSP’04.

Proc.29th IEEE International Conference on

Acoustics, Speech, and Signal Processing.

Gao, H.-Y., 1996. WaveShrink with firm shrinkage,

Technical Report 39, StatSci Division of MathSoft,

Inc.

Gao, H.-Y., 1998. Wavelet Shrinkage de-noising using the

nonnegative garrote, Journal on

Comput.Graph.Statist.

K.Egiazarian, M Helsingius, and J.Astola, 1999. Removal

of Blocking Artifacts using Transform Domain

Denoising, In ISCAS’99.

Egiazarian, K., Astola, J., Helsingius, M., Kuosmanen P.,

1999. On Adaptive Denoising and Lossy Compression

of Images in Transform Domain, Journal of Electronic

Imaging, SPIE.

Pogossova, E., Egiazarian, K., Astola, J., 2003. Signal De-

noising in Tree-Structured Haar-basis, Proc. of 3

International Symposium on Image and Signal

Processing and Analysis.

Öktem,R., Yaroslavsky, L., Egiazarian, K., 1999.

Transform based Denoising Algorithms: Comparative

Study, TICSP Series #9, Tampere, Finland.

Agaian, S.S., Gevorkian, D.Z., 1992. Synthesis of a class

of orthogonal transforms. Parallel SIMD-algorithms

and specialized processors. Pattern Recognition and

Image Analysis.

Minasyan, S., Guevorkian, D., Sarukhanyan, H., 2001. On

parameterized fast Haar- and Hadamard-like

transforms of arbitrary order, In CSIT’01. Proc. of 3

International Conference On Computer Science and

Information Technologies.

Minasyan, S., Astola, J., Guevorkian, D., 2005. An Image

Compression Scheme Based on Parametric Haar-like

Transform. In ISCAS’05. Proceedings of IEEE

International Symposium on Circuits and Systems.

Minasyan, S., Astola, J., Egiazarian, K., Guevorkian, D.,

2006. Parametric Haar-like Transforms in Image

Denoising. In ICIP’06. International Conference on

Image Processing.

0 50 100 150 200 250

-10

0 50 100 150 200 250 300

-10

0 50 100 150 200 250 300

-10

0 50 100 150 200 250 300

-10

Figure 1: Denoising of signal Bumps: a) Original signal, b)

noisy signal (SNR=7dB), c) wavelet denoised signal (soft

thresholded, MSEw=0.7111), and d) signal denoised by

proposed method (thresholded by CTF, w=8,

MSEwp=0.3735).

SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS

139