A TEMPORAL SYNCHRONIZATION MECHANISM FOR

REAL-TIME DISTRIBUTED CONTINUOUS MEDIA

Luis A. Morales Rosales, Saul E. Pomares Hernandez

Computer Science Department,

National Institute of Astrophysics, Optics and Electronics (INAOE)

Luis Enrique Erro No. 1, 72840 Tonantzintla, Puebla, Mexico.

Keywords:

Continuous media, distributed systems, synchronization media, and causal ordering.

Abstract:

The preservation of temporal relations for real-time distributed continuos media is a key issue for emerging

multimedia applications, such as Tele-Immersion and Tele-Engineering. Although several works try to model

and execute distributed continuous media scenarios, they are far from resolving the problem. The present paper

proposes a viable solution based on the identiﬁcation of logical dependencies. Our solution considers two

main components. First, it establishes a temporal synchronization model that expresses all possible temporal

scenarios for continuous media according to their causal dependency constraints. The second component

consists of an innovative synchronization mechanism that accomplishes the reproduction of continuous media

according to its temporal speciﬁcation. We note that the present work does not require previous knowledge of

when nor for how long the continuous media of a temporal scenario is executed.

1 INTRODUCTION

The subject of synchronization for distributed con-

tinuous media addresses the problem of preserving

temporal relations among streams (continuous media)

having geographically distributed sources. The syn-

chronization in this kind of media is carried out with-

out previous knowledge of when or for how long the

streams are or will be executed. Several works at-

tempt to resolve this problem. We can group them ac-

cording to their synchronization model into two broad

categories: synchronous and asynchronous. The main

difference between these categories relates to whether

they consider in some way or not a common reference

(virtual or physical clocks, shared memory, off-line

synchronization, etc). While a common reference is

present in the synchronous category, it is absent in

the asynchronous one. Most works fall into the syn-

chronous category (Allen, 1983; Pantelis et. al, 2000;

Colin, 1998). These works usually try to answer the

synchronization problem by measuring the period of

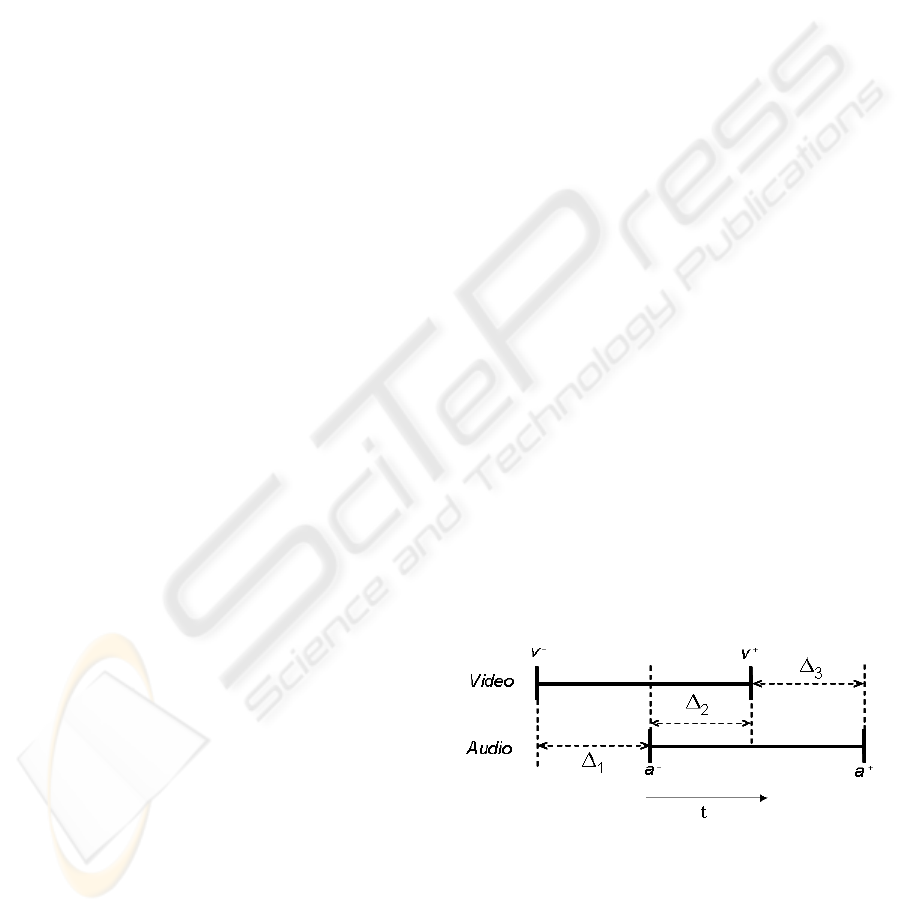
physical or virtual time elapsed (△

) between certain

points in a timeline. Such points can be the begin

−

) and/or end (x

) events of the continuous me-

dia involved (See Fig. 1). Only few works deal with

the problem in an asynchronous manner (Grigoras et.

al, 2003; Grigoras et. al, 2005; Yutaka et. al, 1999;

Chang et. al, 2003; Kshemkalyani, 1996). They pri-

marily take into account logical dependencies instead

of temporal dependencies. One representative work is

the model introduced in (Grigoras et. al, 2003; Grig-

oras et. al, 2005), which determines the possible re-

lations of continuous media by identifying causal de-

pendencies between the begin and end events. For ex-

ample, in Fig. 1, Grigoras et al. establish the overlaps

relation as (v

−

→ a

−

∧ a

−

→ v

∧ v

→ a

Figure 1: Example of a temporal scenario.

Neither approach taken by the works in the two

general categories fulﬁlls the requirements needed to

solve the issue of preserving temporal relationships.

This can be explained by several reasons. First, it is

not easy to have a common reference in distributed

systems since these involve the lack of a global

302

A. Morales Rosales L. and E. Pomares Hernandez S. (2006).

A TEMPORAL SYNCHRONIZATION MECHANISM FOR REAL-TIME DISTRIBUTED CONTINUOUS MEDIA.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 302-309

DOI: 10.5220/0001572403020309

 SciTePress

time clock and shared memory. Second, solely

considering logical dependencies among begin and

end events may result in inaccurate executions. For

example, a synchronization mechanism can ensure

that the reproduction of events fulﬁlls v

−

→ a

−

but the model does not specify how much time must

elapse between the reproduction of v

−

and a

−

In this paper we propose a solution belonging

to the asynchronous category that attempts to resolve

the problem related to possible imprecisions. To

achieve this, we work with the continuous media at

two abstract levels. At the higher level, the temporal

duration is taken into account by representing the

continuous media segments as intervals. At the lower

level, we work with intervals, considering that an

interval is composed of a set of sequentially-ordered

messages. Taking into consideration these two

abstract levels, our synchronization model translates

temporal scenarios to be expressed as subintervals

(segments) arranged according to their logical prece-

dence dependencies. This translation results in the

creation of what we call logical mappings.

The structure of this paper is as follows. We

present in Section 2 the system model, the back-

ground and some required deﬁnitions. The Temporal

Synchronization Model is presented in detail in Sec-

tion 3. We introduce in Section 4 our Synchronization

Mechanism. Finally, conclusions are provided in

Section 5.

2 PRELIMINARIES

2.1 The System Model

Processes: The application under consideration

is composed of a set of processes P = {i, j...},

organized into a group that communicates by reliable

broadcast asynchronous messages. A process can

only send one message at a time.

Messages: We consider a ﬁnite set of messages

M, where each message m ∈ M is identiﬁed by a

tuple m = (p, x), where p ∈ P is the sender of m,

denoted by Src(m), and x is the local logical clock

for messages of p when m is broadcasted. The set of

destinations of a message m is always P .

Events: Let m be a message. We denote by

send(m) the emission event of m by Src(m), and by

delivery(p, m) the delivery event of m to participant

p ∈ P . The set of events associated to M is then the

set E = {send(m) : m ∈ M } ∪ {delivery(p, m) :

m ∈ M ∧ p ∈ P }. The process p(e) of an event

e ∈ E is deﬁned by p(send(m)) = Src(m) and

p(delivery(p, m)) = p. The set of events of a

process p is E

= {e ∈ E : p(e) = p}.

Intervals: We consider a ﬁnite set I of inter-

vals, where each interval A ∈ I is a set of messages

A ⊆ M sent by a participant p = P art(A), deﬁned

by the mapping P art : I → P . Formally, we

have m ∈ A ⇒ Src(m) = P art(A). Due to

the sequential order of P art(A), we have for all

m, m

′

∈ A, m → m

′

or m

′

→ m. We denote by a

−

and a

the endpoint messages of A, such that for all

m ∈ A : a

−

6= m and a

6= m ⇒ a

−

→ m → a

2.2 Background and Deﬁnitions

2.2.1 The Happened-Before Relation for Single

Events

The happened-before relation, also known as the

causal relation, was introduced in (Lamport, 1978).

It is a strict partial order (i.e. irreﬂexive, asymmetric,

and transitive) deﬁned as follows:

Deﬁnition 1. The causal precedence relation, de-

noted by “→”, is the partial order generated by the

following pair:

1. e → e

′

for all e, e

′

such that p(e) = p(e

′

) and e

occurs before e

′

on p(e)

2. send(m) → delivery(k, m) for every message m

and process k

We note that the complement to the causal prece-

dence is the concurrent relation deﬁned as e k e

′

⇒

¬(e → e

′

∨ e

′

→ e). The precedence relation

on messages denoted by m → m

′

is induced by

the precedence relation on events, and is deﬁned by

m → m

′

⇒ send(m) → send(m

′

A behavior or a set of behaviors satisﬁes causal or-

der delivery if the diffusion of a message m causally

precedes the diffusion of a message m

′

, and the deliv-

ery of m causally precedes the delivery of m

′

for all

participants that belong to P . Formally, we have:

Deﬁnition 2. Causal Order Delivery (broadcast

case): If send(m) → send(m

′

), then ∀p ∈ P :

delivery(p, m) → delivery(p, m

′

)

2.2.2 The Partial Causal Relation

The Partial Causal Relation (PCR) was introduced in

(Fanchon et. al, 2004) (Deﬁnition 3). It considers a

subset M

′

⊆ M of messages. The PCR induced by

′

considers the subset of events E

′

⊆ E that denote

′

= {send(m), m ∈ M

′

} ∪ {delivery(p, m), m ∈

′

, p ∈ P }. For any identiﬁer p ∈ P , we have

′

= E

′

∩E

. The partial precedence →

′

⊆ E

′

×E

′

induced by M

′

is the least partial order relation (tran-

sitive and acyclic) on E

′

and it is deﬁned as follows:

A TEMPORAL SYNCHRONIZATION MECHANISM FOR REAL-TIME DISTRIBUTED CONTINUOUS MEDIA

303

Deﬁnition 3. The partial causal relation “→

′

” is

the least partial order relation satisfying the two fol-

lowing properties:

1. For each participant p ∈ P , the local restrictions of

→

′

and → to the events of E

′

coincide: ∀e, e

′

∈

′

: e → e

′

⇔ e →

′

2. For each message m ∈ M

′

and p ∈ P ,

the emission of m precedes its delivery to p:

send(m) →

′

delivery(p, m).

2.2.3 Happened-Before Relation for Intervals

In (Lamport, 1986) it was established that an inter-

val A precedes or happens before another interval B

if all elements that compose interval A causally pre-

cede all elements of interval B. This deﬁnition is used

in the model presented in Section 3. However, it is

well known that causal ordering implicates a com-

putational high cost in terms of overhead, delay and

processing time. For this reason, in order to reduce

the cost, our mechanism presented in Section 4 uses

the deﬁnition of the happened-before relation for in-

tervals that was proposed in (Morales, 2005) (Deﬁni-

tion 4) which is expressed only in terms of the inter-

val endpoints. This deﬁnition says that if the elements

of an interval are sequentially ordered, then ensuring

partial causal order (Deﬁnition 3) on the interval end-

points is sufﬁcient to ensure causal ordering at an in-

terval level.

Deﬁnition 4. The relation “→

” on the set of in-

tervals I of a system is accomplished if it satisﬁes the

following two conditions:

1. A →

B if a

→

′

−

2. A →

B if ∃C|(a

→

′

−

∧ c

→

′

−

)

where a

and b

−

are the right and left endpoints

(messages) of A and B, respectively, c

−

and c

are

the endpoints of C, and →

′

is the partial causal or-

der (Deﬁnition 3) induced on M

′

⊆ M where M

′

, is

the subset composed by the endpoint messages of the

intervals in I. The second condition is the transitive

property. Now, we present the simultaneous relation

for intervals as follows:

Deﬁnition 5. Two intervals, A and B, are said to

be simultaneous “|||” if the following condition is sat-

isﬁed:

A|||B ⇒ a

−

k b

−

∧ a

k b

Finally, we present the deﬁnition of causal delivery

for intervals based on their endpoints as follows:

Deﬁnition 6. Causal Broadcast Delivery for Inter-

vals

If (a

, b

−

) ∈ A×B, send(a

) →

′

send(b

−

) ⇒

∀p ∈ P, delivery(p, a

) →

′

delivery(p, b

−

), then

∀p ∈ P, delivery(p, A) →

delivery(p, B)

2.3 Temporal Synchronization

Model

In order to achieve the synchronization between con-

tinuous media in distributed systems, we propose to

determine temporal relations based on the identiﬁca-

tion of logical precedence dependencies. To achieve

this, we translate temporal scenarios to be expressed

in terms of the precedence relation and the simulta-

neous relation; we call these translations logical map-

pings. More explicitly, in our work, a logical mapping

decomposes a temporal scenario into data segments

(events) that are arranged according to their possible

precedence dependencies.

2.4 Logical Mappings

The process to create logical mappings (Table 1) in-

volves taking every pair of intervals in the system that

compose a temporal scenario, and translating each

pair into four data segments, which are determined

according to the possible precedence dependency of

the discrete events that compose them. These data

segments, according to our deﬁnition, become new

intervals. The resulting intervals are only expressed

in terms of the happened-before relation and the si-

multaneous relation

Table 1: Logical Mapping.

∀(X, Y ) ∈ I × I

A(X, Y ) ← • {x ∈ X : x → y

−

}

if x

−

→ y

−

• ⊘ otherwise

B(X, Y ) ← • {y ∈ Y : x

→ y}

if x

→ y

• {x ∈ X : y

→ x}

if y

→ x

• ⊘ otherwise

C(X, Y ) ← X − (A(X, Y ) ∪ B(X, Y ))

D(X, Y ) ← Y − B(X, Y )

W (X, Y ) ← C|||D

S(X, Y ) ← A →

W →

In order to consider the seven basic relations and

their inverses, and to maintain the model simpliﬁed,

we ﬁrst identify the X and Y intervals for each pair

of intervals in the system. The X interval will be the

interval with the ﬁrst left endpoint, and the Y interval

will be the remaining interval. This is done to ensure

We consider in our work that an interval can be empty.

In such case, the following properties apply:

• ⊘ →

A ∨ A →

⊘ = A

• ⊘|||A ∨ A|||⊘ = A

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

304

Figure 2: X overlapsY relation and its logical mapping

A →

(C|||D) →

that for every pair, x

−

→ y

−

or x

−

||y

−

at all times.

Once the X and Y intervals are identiﬁed, the model

segments each pair into four subintervals, A, B, C

and D (see Table 1). We now proceed to construct

the general causal structure S = A →

W →

where W determines if overlaps exist between the

present pair. For example, for the overlaps relation

deﬁned in (Allen, 1983), the logical mapping is equal

to A →

(C|||D) →

B (See Fig. 2). Our model

deﬁnes ﬁve possible logical mappings (Table 2, right

column), which we call: precedes, overlaps, ends,

starts, and simultaneous. These ﬁve logical mappings

are sufﬁcient to represent the thirteen relations estab-

lished in (Allen, 1983). As shown in Table 2, we are

now able to express every possible temporal relation

by only considering the interval happened-before re-

lation and the interval simultaneous relation.

2.5 Synchronization Mechanism

Our synchronization mechanism carries out two

main functions that allow the continuous media to be

presented according to the temporal model previously

presented. The ﬁrst function makes the translation of

temporal relations (logical mappings), and the second

function ensures the presentation of the intervals

(data segments) according to the resultant logical

mapping.

In order to carry out the temporal synchroniza-

tion, our mechanism, which is based on the resultant

logical mapping, determines if an interval must begin

to be delivered or not according to whether it satisﬁes

or not its causal dependency. For example, in Figure

2, interval A precedes interval D. Therefore, interval

D will not begin to be delivered until all messages

of A have been delivered. When the intervals are

simultaneous in this case, C and D, the messages of

C can be delivered in any order with respect to the

messages of D.

General description. Internally, the mecha-

nism uses two kinds of ordered messages: causal

messages and FIFO messages. We have three differ-

ent causal messages: begin, end, and cut. The begin

and end messages are the left and right endpoints of

the original intervals, and cut is a control message

used by the mechanism to inform about an interval

segmentation. FIFO messages (fifo

p) are used

only inside an interval. We note that all causal and

FIFO messages carry data of the continuous media

involved. In order to ensure the causal order delivery

at an interval level according to Deﬁnition 6, our

algorithm uses vector clocks (Fidge, 1989) and the

immediate dependency relation (IDR) (Pomares et.

al, 2004). We use the IDR relation to determine the

sufﬁcient causal control information that must be

attached per message. Next, we describe the main

components of the mechanism.

2.6 Data Structures

Local states. The state of a process p is de-

ﬁned by three data structures: V T (p), CI(p) and

last

fifo(p).

• V T (p) is the vector time. For each process p there

is an element V T (p)[j] where j is a process identi-

ﬁer. A process can only send one message at a time.

The size of V T is equal to the number of processes

in the group. The element V T (p)[j] represents the

greatest number of messages of the identiﬁer j and

“seen” in causal order by p. It is through the V T (p)

structure that we are able to guarantee the causal

delivery at an interval level.

• CI(p) is the control information structure. It is

a set of entries c

k,t

= (k, t) where (k, t) is a mes-

sage identiﬁer (the message diffused by the process

identiﬁer k with the local message clock value t).

Structure CI(p) also contains information about

the causal history of p.

• last

fifo(p) is the ﬁfo control information

structure. It is a structure composed by a set of

entries (k, t), where (k, t) is a message identiﬁer.

The last

fifo structure has information about

the last (f if o

p) messages received by p. These

(fifo

p) messages represent potential causal

messages.

Messages. The mechanism uses causal messages

(begin, end, cut) and FIFO messages (f if o p). A

message m, in general, is composed of an iden-

tiﬁer (k, t), an attached causal information H(m),

and continuous media data in the structure called

data. For f if o p messages, structure H(m) is al-

ways H(m) = ⊘. Formally, a message m is a tuple

m = (k, t, T P, H(m), data), where:

• k is the identiﬁer of sender k = Src(m).

• t = V T (p)[k] is the (local) clock value of p for the

identiﬁer k when a causal message m (begin, end,

A TEMPORAL SYNCHRONIZATION MECHANISM FOR REAL-TIME DISTRIBUTED CONTINUOUS MEDIA

305

Table 2: Allen’s relations and their corresponding logical mappings.

Allen’s

Relations

Endpoints

Interval Temporal

Relation

Logical Mappings

Xbefore Y x

→ y

−

Precedes:

Y after X A →

Xmeets Y x

||y

−

Y meet-by X

Xoverlaps Y x

−

→ y

−

→ x

∧ Overlaps:

Y overlap-by X x

→ y

A →

(C|||D) →

Xincludes Y x

−

→ y

−

∧

Y during X y

→ x

Xstarts Y x

−

k y

−

∧ Starts:

Y started-by X x

→ y

(C|||D) →

Xﬁnishes Y x

k y

∧ Ends:

Y ﬁnished-by X x

−

→ y

−

A →

(C|||D)

Xequals Y x

−

k y

−

∧ Simultaneous:

k y

C|||D

or cut) is sent. The value of t indicates the sequen-

tial number to which causal message m belongs.

• T P is the type of message

(begin, end, cut, fifo

p).

• H(m) contains identiﬁers of messages (k, t)

causally preceding causal message m, which de-

notes the begin and/or end of other intervals. The

information in H(m) ensures the causal delivery

of message m. Structure H(m) is built before a

causal message is broadcasted, and then it is at-

tached to the causal message.

• data is the structure that carries the media data.

2.7 Example Scenario

Construction of logical mappings. We explain the

creation of logical mappings in the example of the

overlaps relation shown in Fig. 3. The referenced

lines correspond to the code shown in the Table 3.

In this example, segment A must ﬁrst be determined.

To achieve this, we map the left causal boundary

−

with the begin send event send( x

−

= x

and the right causal boundary with the send event

send(a

= x

). The right endpoint a

is deter-

mined by the last (fifo

p) message received by par-

ticipant j before the begin send event send(y

−

) (lines

16-20). Once we know the causal boundaries of A,

we determine the set of messages that compose it

(A = {x

, x

, ..., x

}). After interval A is identiﬁed,

we proceed to determine the causal boundaries of C

and D. At this point, we can identify the left causal

boundaries c

−

= x

k+1

and d

−

= y

. However, it

is only until the end send event of endpoint x

and

its corresponding delivery event that we can identify

the right endpoints of C and D. With the end send

event send(x

= x

) we establish that c

= x

and consequently, C = {x

k+1

, x

k+2

, ..., x

}. At

the reception of x

by participant j, our algorithm

sends a cut message (lines 49-51) which establishes

the end of interval D(d

= y

) and the beginning

of interval B(cut = b

−

= y

l+1

). As a result, we

have D = {y

, y

, ..., y

}. Finally, with the send

event of y

, we have b

= y

, and consequently,

B = {y

l+1

, y

l+2

, ..., y

In general, our mechanism considers three impor-

tant rules to create logical mappings:

1. When x

−

→ y

−

: the right endpoint a

is deter-

mined by the last (f ifo

p) message received by

participant j before the send event of y

−

, where

j = P art(Y ).

2. When x

→ y

: at the reception of x

by par-

ticipant j, we generate on j a cut message (only if

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

306

Table 3: Speciﬁcation of the synchronization mechanism.

Initially

1. V T (p)[j] = 0, ∀j : 1, ..., n

2. CI(p) ← ⊘

3. last f if o(p) ← ⊘

4. Act = 0

For each message m diffused by p with the process identiﬁer i

5. send(Input : T P = {begin|end|cut|fifo p})

6. V T (p)[i] = V T (p)[i] + 1

7. If not (T P = f ifo p) then

8. If not (T P = begin) then /*Construction of the H(m)for end and cut messages*/

9. H(m) ← CI(p)

10. if (T P = end) then

11. Act = 0 /*Indicates that process p is inactive*/

12. endif

13. else /*Construction of the H(m) for begin messages*/

14. Act = 1 /*Indicates that process p is sending an interval*/

15. ∀(s, r) ∈ CI(p)

16. if ∃(x, l) ∈ last f if o(p) | s = x then /*Adding info about f ifo p messages

to CI(p)*/

17. if not ((s, r) = max{(x, l), (s, r)}) then

18. CI(p) ← CI(p) ∪ (x, l)

19. endif

20. endif

21. H(m) ← CI(p)

22. last f if o(p) ← ⊘

23. endif

24. CI ← ⊘ /*Erases the CI(p) on each causal message sent*/

25. else */Construction of the H(m) for f if o p messages*/

26. H(m) ← ⊘

27. endif

28. m = (i, t = V T (p)[i], T P, H(m), data)

29. sending(m)

For each message received by p with process identiﬁer j

30. receive(m) in p with i 6= j and m = (k, t, T P, H(m), data)

31. If t = V T (p)[k] + 1 then /* FIFO delivery condition*/

32. If not (T P = f ifo p) then

/*Causal delivery condition*/

33. If not (t

′

≤ V T (p)[l])∀(l, t

′

) ∈ H(m)) then

34. wait()

35. else /*Causal delivery procedure*/

36. delivery(m)

37. V T (p)[k] = V T (p)[k] + 1

A TEMPORAL SYNCHRONIZATION MECHANISM FOR REAL-TIME DISTRIBUTED CONTINUOUS MEDIA

307

38. If ∃(s, r) ∈ CI(p) | k = s then

39. CI(p) ← CI(p) \ {(s, r)}

40. endif /*Updating CI(p) with a more recent message*/

41. CI(p) ← CI(p) ∪ {(k, t)}

42. ∀(l, t

′

) ∈ H(m) /*Clears CI(p) and last fifo(p) */

43. If ∃(s, r) ∈ CI(p) | l = s and r ≤ t

′

then

44. CI(p) ← CI(p) \ (s, r)

45. endif

46. If ∃(x, l) ∈ last f if o(p) | l = x and l ≤ t

′

then

47. last f if o(p) ← last f if o(p) \ (x, l)

48. endif

49. If Act = 1 and not(T P = cut) and not(T P = begin) then

50. send(cut) /*Sending a cut message*/

51. endif

52. endif

53. else /*FIFO delivery procedure*/

54. delivery(m)

55. V T (p)[k] = V T (p)[k] + 1

56. If ∃(x, l) ∈ last f if o(p) | k = x then

57. last f if o(p) ← last f if o(p) \ (x, l)

58. endif /*Updating last f if o(p) with a more recent message*/

59. last f if o(p) ← last f ifo(p) ∪ (k, t)

60. endif

61. else

62. wait()

63. endif

j is sending an interval), which determines the be-

ginning of interval B (cut = b

−

= y

l+1

) and the

end of interval D(d

= y

3. When y

→ x

: at the reception of y

participant i = P art(X), we generate on i a

cut message (only if i is sending an interval),

which determines the beginning of interval B

(cut = b

−

= x

q+1

) and the end of interval

C(c

= x

Carrying out causal order delivery. The re-

sultant logical mapping for the example scenario is

A →

(C|||D) →

B. To ensure interval causal

delivery in terms of their endpoints (Deﬁnition 6) we

need to ensure that:

• delivery(a

) →

′

delivery(c

−

• delivery(a

) →

′

delivery(d

−

• delivery(c

) →

′

delivery(b

−

) and

• delivery(d

) →

′

delivery(b

−

)

Since a

= x

, c

−

= x

k+1

, d

= y

and b

−

= y

l+1

, the procedure of deliv-

ery(a

) →

′

delivery(c

−

) and delivery(d

)

→

′

delivery(b

−

) is accomplished by the FIFO

property implemented by lines 6 and 31. The

procedure of delivery(a

) →

′

delivery(d

−

) is ac-

complished in the following way. Initially, message

= x

is sent as fifo

p. To consider it as a causal

message, process j includes information concerning

in its causal history (lines 16-20), and attaches

this information to structure H(m) of the message

−

= y

before its send event (line 21).

The causal delivery condition (line 33) ensures

that the beginning of interval D (d

−

) will be de-

livered only after the delivery of x

, and the FIFO

condition (line 21) ensures that x

will be delivered

only after the delivery of all messages x

∈ A ⊆ X,

such that h < k . For the requirement of delivery(c

)

→

′

delivery(b

−

), message b

−

= y

l+1

has attached

information on its structure H(m) about the message

= x

(lines 15-21). The causal delivery condition

(line 33) ensures that the beginning of interval B

−

) will be delivered only after the delivery of x

and the FIFO condition (line 21) ensures that x

will

be delivered only after the delivery of all messages

∈ C ⊆ X, such that q < n.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

308

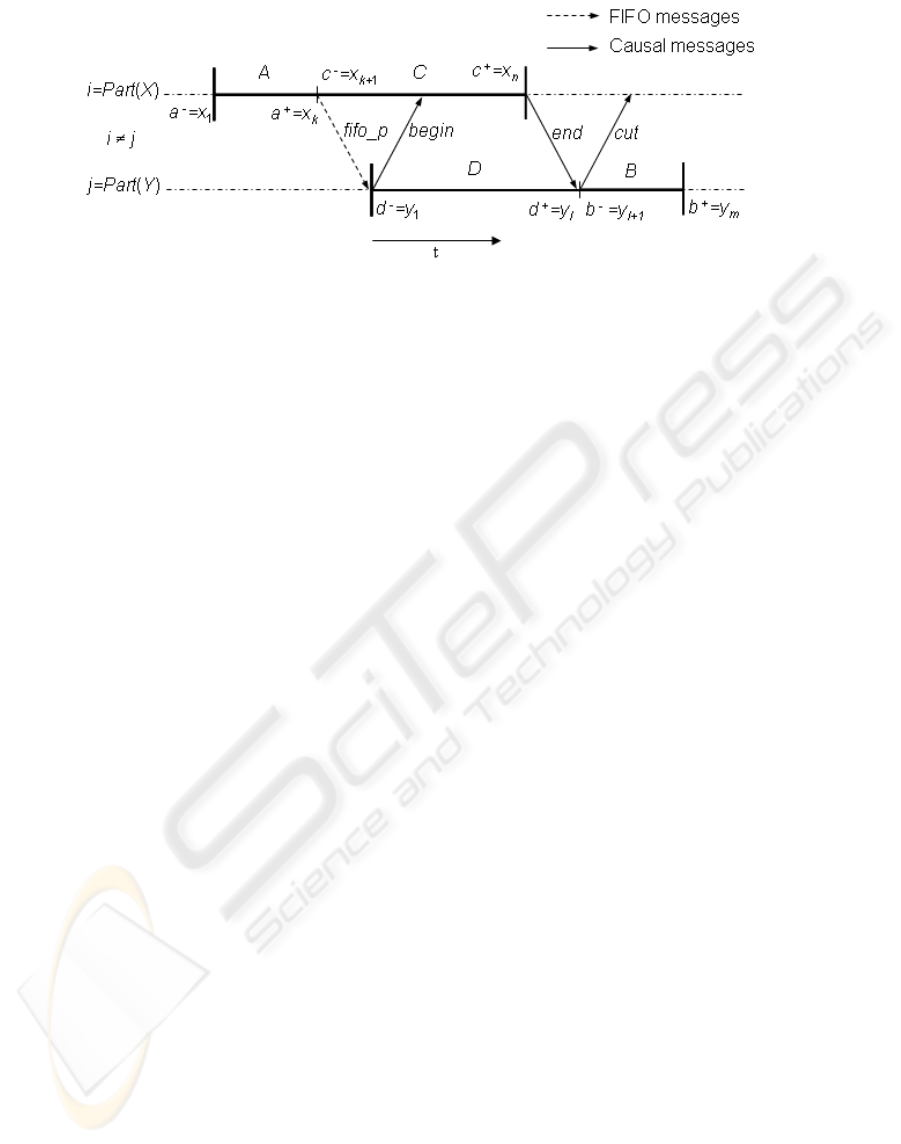
Figure 3: Construction of the logical mapping (A →

(C|||D) →

B) for the overlaps relation.

3 CONCLUSIONS

An innovative temporal synchronization mechanism

has been presented. The mechanism addresses in

an asynchronous manner the problem of preserv-

ing temporal relations for real-time distributed media

streams. The core of our mechanism is the delivery

of streams according to the resultant logical mapping

which is based on the causal dependencies of the con-

tinuous media involved. The mechanism uses the par-

tial causal relation and the immediate dependency re-

lation to reduce the causal overhead. Further work is

needed to enhance our mechanism so that it can sup-

port real network conditions (loss of messages, life-

time of messages, etc.). Our attention is focused in

this direction, and we expect to publish some interest-

ing contributions shortly.

REFERENCES

James F. Allen. (1983). Maintaining Knowledge about

Temporal Intervals. In Communications of the ACM,

Vol 26, Num 11, 832-843.

Pantelis Balaouras, Ioannis Stavrakakis, Lazaros F. Mer-

akos. (2000). Potential and Limitations of a Teleteach-

ing Environment based on H.323 Audio-Visual. In

Communication Systems. Computer Networks, Vol 34,

Num 6, 945-958.

Colin Perkins. (2003). RTP Audio and Video for Internet.

Addison Wesley, USA, ISBN: 0672322498.

Romulus Grigoras, Philippe Mauran, Girard Padiou,

Philippe Queinnec. (2003). Ordonnancement Causal

de Flux Repartis Multimedias. In Formalisation des

Activites Concurrentes FAC’2003.

Cezar Plesca, Romulus Grigoras, Philippe Queinnec, Girard

Padiou. (2005). Streaming with Causality: A Practical

Approach. In ACM Multimedia 2005, Singapore, 6-

11.

Yutaka Ishibashi, Shuji Tasaka, Yoshiro Tachibana. (1999).

A Media Synchronization Scheme with Causality

Control in Network Environments. In Proceedings

26th Conference on Local Computer Networks, Low-

ell, Massachusetts, USA, IEEE Computer Society,

232-241.

Anthony Y. Chang, Jason C. Hung. (2003). An Integrated

Temporal Composition Model for Synchronization

Speciﬁcation. In Proceedings of the 17th Interna-

tional Conference on Advanced Information Network-

ing and Applications (AINA’03), 2003, Xi’an, China.

IEEE Computer Society 2003, ISBN 0-7695-1906-7,

189-193.

Kshemkalyani Ajay D. (1996). Temporal Interactions of

Intervals in Distributed Systems. In Journal of Com-

puter and System Science, Vol 52, Num 3, 287-298.

Lamport L. (1978). Time, Clocks, and the Ordering of

Events in a Distributed System. In Communications

ACM, Vol 21, Num 7, 558-565.

Fanchon J, Drira K, Pomares Hernandez S. (2004). Abstract

Channels as Connectors for Software Components in

Group Communication Services. In Fifth Mexican In-

ternational Conference on Computer Science (ENC

2004), IEEE Computer Society, 88-95.

Lamport L. (1986) On Interprocess Communications: I.

Basic Formalism. In Distributed Computing, 1, 77-85

Luis Morales. (2005). Algoritmo de Sincronizaci

on de

Flujos Continuos en Tiempo Real. Master’s Thesis

in Computer Science, INAOE. Num. XM1086. Clas-

siﬁcation: XMM -M67-2005-XM1086, Tonantzintla

Puebla, Mexico.

Mattern Fidge. (1989). Virtual Time and Global States of

Distributed Systems. In Parallel and Distributed Al-

gorithms, North-Holland, 215-226.

Pomares Hernandez S, Fanchon J, Drira K. (2004). The

Immediate Dependency Relation: an Optimal Way to

Ensure Causal Group Communication. Annual Re-

view of Scalable Computing, Editions World Scien-

tiﬁc, Series on Scalable Computing, Vol 6, 2004, pp

61-79.

A TEMPORAL SYNCHRONIZATION MECHANISM FOR REAL-TIME DISTRIBUTED CONTINUOUS MEDIA

309