SCATTERING COEFFICIENTS OVER 3-D FLAT DIELECTRIC

SURFACES

Iñigo Cuiñas, Manuel García Sánchez, Ana V. Alejos

Dept. Teoría do Sinal e Comunicacións, Universidade de Vigo, ETSE Telecomunicación, Rúa Maxwell, 36310 Vigo (Spain)

David Martínez

Dept. Ingeniería Eléctrica, Universidad de Oviedo, Ed. Polivalente de Viesques, Mod.8, 1, Gijón (Spain)

Keywords: Reflection, scattering, dielectric surface.

Abstract: Indoor radio channel planning tools implement different models to simulate propagation mechanisms as

transmission or reflection. Specular reflection formulation is commonly used instead of more complex

scattering models, as that is easier programmed as well as it is faster than scattering. In this work, results

from measurements are presented, and modelled by means of traditionally reflection procedures, as well as

by applying scattering pattern computations. Beckmann’s scattering model is used as it was formulated, and

then modified to take into account antenna pattern effects in the measurements. Comparison between

measurements and simulations are also presented, showing good agreement.

1 INTRODUCTION

Indoor radio channel propagation is strongly

conditioned by the environment. In this way, radio

link performance considerably varies depending on

the existence of line of sight between transmitter and

receiver, as well as on the multipath pattern of the

scenario. So, as building structure and furniture are

determinant elements in the definition of multipath,

they also determine the indoor radio link

performance.

Several models have been developed to analyse the

result of the incidence of a propagating wave on a

surface. That phenomenon can be limited to the

main direction, being known as reflection, or

considered all around. Any obstacle in the radio

channel generates its own scattering pattern, which

depends on the electromagnetic characteristics of the

material, the surface roughness, the frequency, and

the angle of incidence. Along this paper,

measurement results are presented, showing that

there are several scattering directions as important as

the main reflection one. And so, models that just

consider the reflection but not the scattering can not

be accurate in low reflective environments.

A Physical Optics based model is presented, and

compared to measurement results in the 5.8 GHz

band. Various slides of different materials have been

used as obstacles to force scattering phenomena, and

measurements have been taken. Simulation and

measurement results fit better than previous models.

Results provided can be used in simulation tools. If

just needing a fast and accurate planning tool, a

good modelling of reflection phenomena is enough.

But the actual word is more complicated than the

simulated one: instead of reflection, scattering is the

result of the incidence of a wave on an obstacle of

any kind, even on a flat soft wall.

Section 2 contains the description of the

measurement set-up used, as well as the

measurement campaign performed. Section 3

contains the models used to obtain the

electromagnetic characterisation from specular

reflection measurements. Section 4 describes the

Physical Optics based Beckmann formulation to

describe the scattering in the incidence region.

Finally, sections 5 and 6 show the results obtained

and the conclusions extracted.

2 SCATTERING MEASUREMENT

OVER STRUCTURAL

ELEMENTS

2.1 Measurement Set-up

The procedure to measure the scattering pattern due

to a wall consists of illuminating it with a directive

194

Cui

nas I., Garc

ıa S

anchez M., V. Alejos A. and Mart

ınez D. (2006).

SCATTERING COEFFICIENTS OVER 3-D FLAT DIELECTRIC SURFACES.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 194-199

 SciTePress

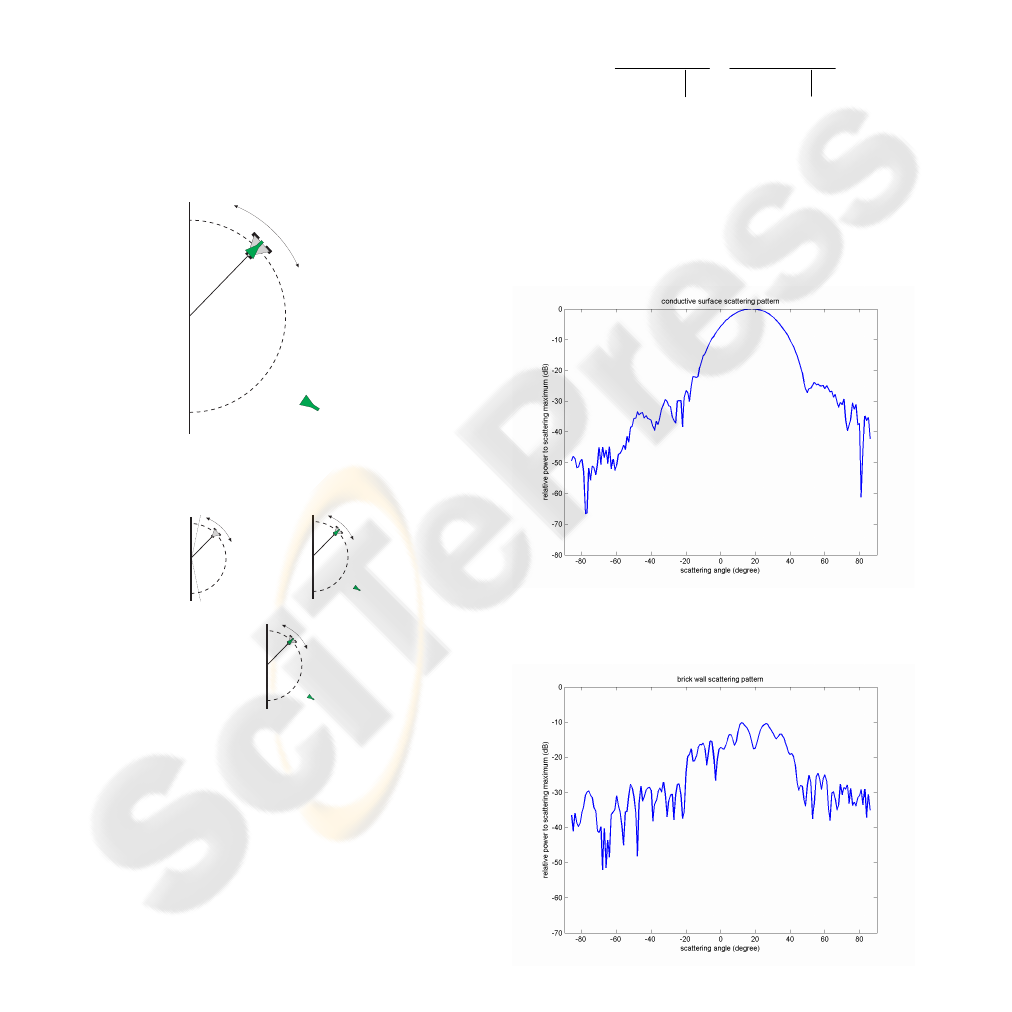
transmitting antenna, while a receiver antenna is

moved, plotting a semi circumference centred in the

incidence point of the transmission. The receiver

antenna is always pointed to the transmitter target.

Transmitter antenna is placed at a fixed angle

respect to the normal to obstacle surface, in a static

location. Receiver antenna locations are selected

along an arc, jumping one degree between adjacent

ones. An automated set up has been designed and

built, integrating the mechanical movement to the

vector network analyser control.

The mechanical system performs the measurement

in three steps, described in figure 2. Reflection due

to metallic slab is used as a reference (unitary

amplitude) to determine the reflection coefficient

due to the wall.

A vector network analyser has been used to sweep

the spectrum between 5.725 and 5.875 GHz, at each

position.

Figure 1: Measurement set-up.

Metallic

slab

Material

under test

Figure 2: Measurement procedure.

2.2 Measurement Campaign

Reflection and scattering coefficients due to a wall,

for different incidence angles, are obtained by

comparing measurement outcomes from the obstacle

and from the metallic slab. Materials considered are

the metallic surface, used as a reference, a brick

wall, and a chipwood panel.

At each receiver location, at a fixed incidence angle,

the measured frequency response includes the

coupling between antennas, the reflection

contribution on the obstacle, and a complete

multipath pattern. Filtering in time domain, all

contributions but reflection on the wall are

eliminated, resulting the amplitude and phase of the

field received after reflection. The scattering pattern

at a fixed incidence angle is obtained applying the

previous procedure to all receiving locations.

Reflection coefficient for metallic slab is assumed to

be -1; and scattering coefficients are defined by

equation:

spec

slabmetallic

obstacle

spec

slabmetallic

obstacle

,21

−

=Γ

(1)

From measurement outcomes, and computing a

value at each observation angle, a scattering pattern

is obtained at each incidence angle.

Figures 3 to 5 show measured scattering patterns in

the 5.8 GHz band, with parallel polarization,

corresponding to a metallic surface, a brick wall and

a chipwood panel. They are obtained for an angle of

incidence of 20 degree.

Figure 3: Measured scattering pattern for conductive

surface, parallel polarisation, incidence 20 degree.

Figure 4: Measured scattering pattern for brick wall,

parallel polarisation, incidence 20 degree.

SCATTERING COEFFICIENTS OVER 3-D FLAT DIELECTRIC SURFACES

195

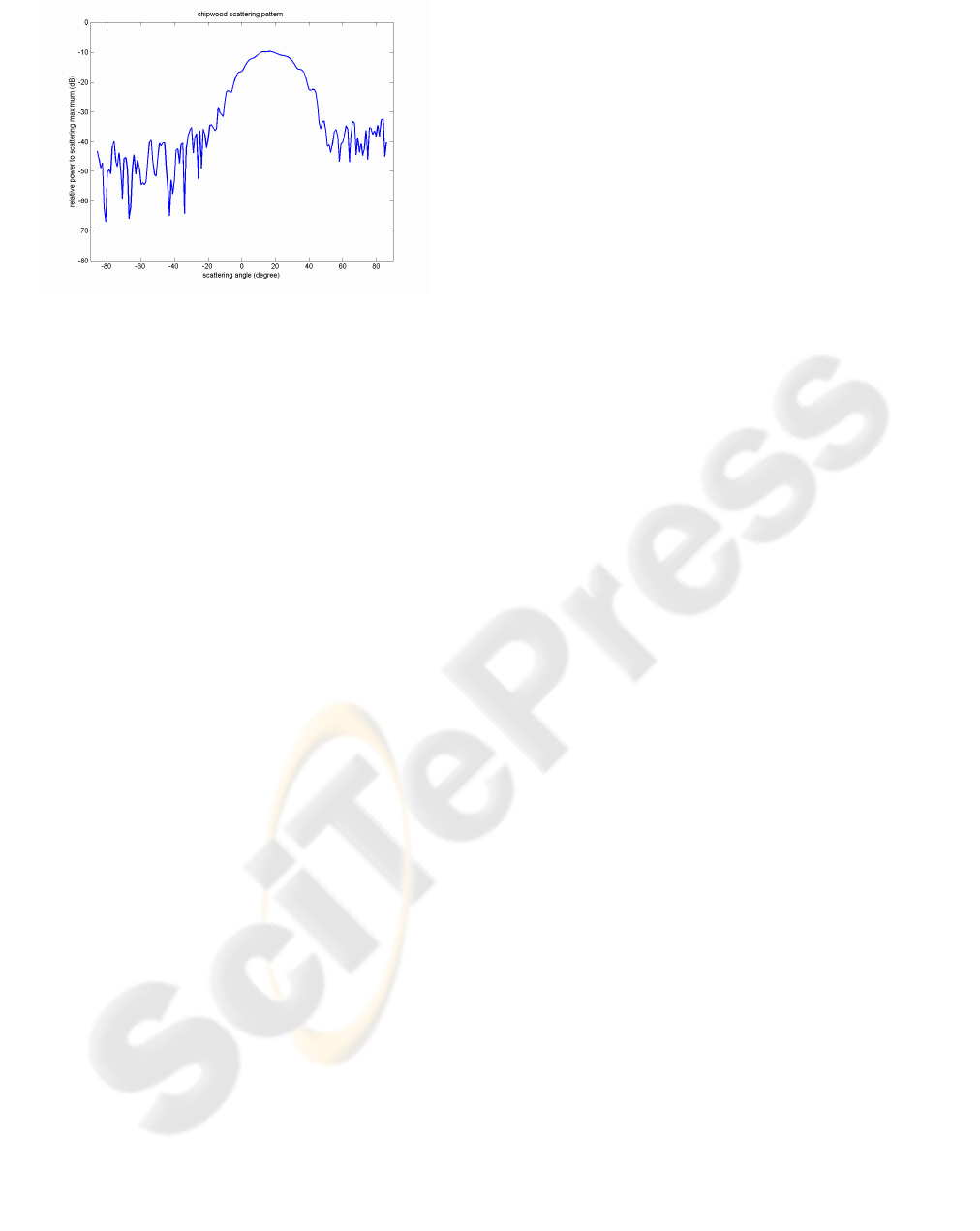
Figure 10: Multilayer model geometry.

Internal successive reflections model tries to explain

the transmission and reflection phenomena as a

result of the coherent sum of several multipath

components generated in both boundaries of the

obstacle with free space.

Multilayer model is intended to explain the

behaviour of complex slab obstacles, which can be

composed by several superposed layers.

All these models use the electromagnetic parameters

of the materials composing the obstacle to compute

transmission and reflection coefficients, in a more or

less complicated formulation.

4 CHARACTERISATION OF

SCATTERING COEFFICIENTS

As shown by measurements, the effect of walls over

propagating waves is considerably more complex

than just specular reflection. The incidence of a

wave on a wall generates a scattering phenomenon

in all space directions, defining a scattering pattern.

4.1 Beckmann Model

A good characterisation of scattering due to rough

surfaces has to include all-direction effects.

Beckmann’s formulation fits this condition, and it is

a classical method to characterise this kind of

surfaces (Beckmann 1987). So, it is used in the

processing of the measurement results.

Reflected and scattered fields are the basis to define

the scattering coefficients. Figure 11 gives the axis

criterion of the model.

The rough surface is defined by ξ, being z=0 its

mean level. It is assumed the mean extended to z>ξ

is the free space.

),( yx

(2)

The electric field strength, as well as its derivative

respect to surface normal, are estimated by using

Kirchhoff approximations (Physical Optics). So, it

can be assumed the total field in a point on the

surface is the same that in a tangent plane to the

surface at the same point. The larger the roughness

curvature radius is, the better the approximation is.

Figure 11: Beckmann model geometry.

One-dimensional rough surfaces are defined by the

following equation:

)(),( xyx

(3)

So, normal vector to surface is always in XZ plane,

and local incidence angle is defined by:

))('arctan(

−=

(4)

Scattering coefficient is defined from the field

scattered in any direction and that reflected in the

specular direction by a flan perfectly conductive

surface with the same size of the obstacle:

surfaceconductivereflected

scattered

,20

(5)

Assuming an electrically large obstacle, presenting a

surface extended from x=-L to x=L, the scattering

coefficient is defined as:

∫

−

⋅−=

jvxjv

dxeba

)'(

cos4

(6)

where

zkxsinsinkv

)cos(cos

)(

2121

+−−=

cos)1(cos)1(

sin)1(sin)1(

θθ

Γ−−Γ+=

−=

This is the general formulation of scattering

coefficient by Kirchhoff approximation. This

equation can be simplified in those situations the

integral has analytical solution, or can be extended

to random surfaces which pattern is defined by its

statistics instead of a deterministic function.

If the surface is flat, ξ=0 and ξ'=0. Then, the

equation is transformed into

)(

cos2

)(

cos2

Lvsinc

Lvsinb

θθ

−

=⋅

−

(7)

SCATTERING COEFFICIENTS OVER 3-D FLAT DIELECTRIC SURFACES

197

Besides, if the surface is perfectly conductive, and

the electric field is polarised perpendicularly to

incidence plane (vertical polarisation in the

measurement campaign), scattering coefficient can

be defined as:

)(

Lvsinc

(8)

With finite conductivity surfaces, there is no general,

exact and explicit solution, but some approximations

can be applied. Generally, these solutions come from

converting a and b in constants using their means for

any local incidence angles. When surface pattern

ξ(x) is symmetric, this mean value can be obtained

from Γ(θ=θ1). A more simply approximation is

obtained by multiplying by Γ(θ=θ1) the scattering

coefficient assumed perfectly conductive. This will

be a good approximation in situations when

{}

)('arctanmax

<<x

, (9)

which is fitted by surfaces with soft slopes, or with

large curvature radii.

As a general conclusion, scattering due to non-

conductive surfaces is affected by finite conductivity

only if local reflection coefficients are dominated by

local incident angle more than by electromagnetic

properties of scattering material.

4.2 Application of Beckmann

formulation

Application of Beckmann formulation is planned by

three different strategies. Successive proposals have

growing computational cost and complexity, but

they give better concordance to actual situations.

This can be checked by comparison with

measurements. Obstacles are considering with flat

surface and with determined electromagnetic

characteristics.

First option (figure 12) consist on the direct

application of Beckmann formulation, considering

an incidence field on a flat surface, with an

incidence angle determined by direct propagation

path between transmitter antenna and the centre of

illumination. This case does not consider the

radiation pattern of the antenna.

Second option (figure13) is more advanced and

consists on dividing the surface in several parallel

segments of the same width and assumed infinite

length. Local incidence angle at each segment is

taken into account when applying Beckmann

method.

Figure 12: Direct application of Beckmann model.

Figure 13: Application of Beckmann model by segments.

Figure 14: 3D Application of Beckmann model.

Third option (figure 14) consists on determine the

illuminated surface on the obstacle, taking into

account the radiation pattern of the transmitter

antenna (Arias 1996). This surface is divided into

rings, and then each ring is divided in several

patches. Beckmann formulation is applied on each

patch, considering the local incidence angle at each

of them.

5 RESULTS

In this section, outcomes from measurement

campaign are presented and explained. First among

them are related to electromagnetic characterisation

of different materials from specular reflection

induced effects. Then, measured scattering patterns

are compared with those computed by applying

Beckmann formulation following the three strategies

previously described.

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

198

Once reflection coefficients are measured, and

applying the three models exposed in previous

section, the electromagnetic characterisations of

brick wall and the chipwood panel have been

obtained. The fitting of reflection models provides

the electromagnetic characteristic parameters of each

material (dielectric constant: 5.0-j0.2 for brickwall,

and 3.3-j0.1 for chipwwod). Using these

characteristic parameters, and taking into account

the geometric distribution of the experimental

elements (obstacle, transmitter and receiver antennas

relative locations), Beckmann formulation was

applied following the three strategies enunciated in

previous section.

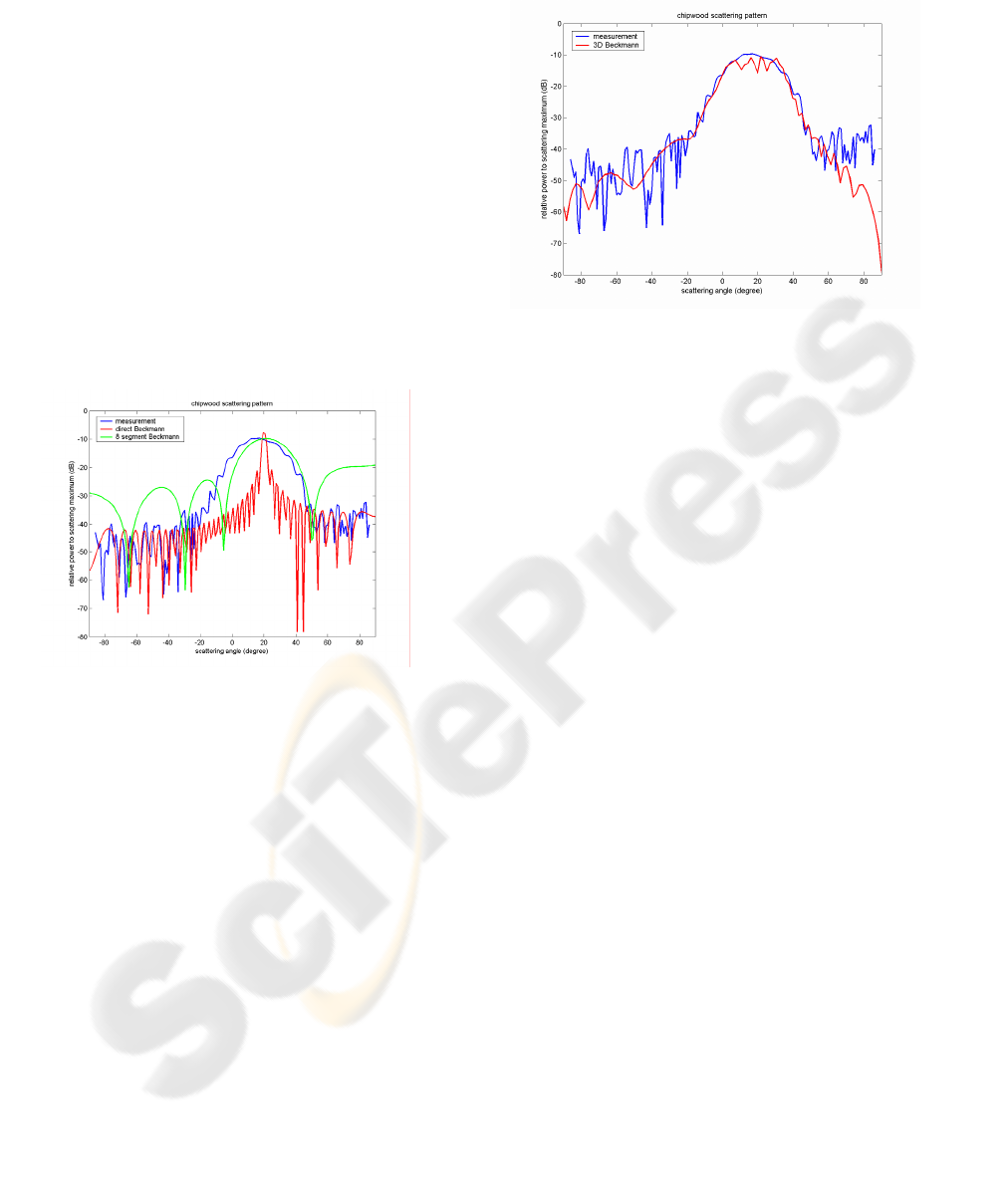
Comparisons among measured scattering patterns

and computed patterns using Beckmann in one step,

by segments, and by patching the illuminated area

are shown in figures 15 and 16. Results indicate

better fitting when Beckmann application takes into

account the geometry of the problem.

Figure 15: Scattering patterns, chipwood panel, parallel

polarisation, incidence 20 degree.

6 CONCLUSION

Results of a measurement campaign of scattering

pattern over flat obstacles are presented. From

measurement outcomes, the involved materials are

electromagnetically characterised in the 5 GHz band.

Moreover, modelling of scattering patterns

generated by flat obstacles is proposed, based on

Beckmann formulation. Among three possible

strategies of implementation, that based on patching

the illuminated area on the obstacle surface, and then

considering local contributions from every patch, is

tested and provides the best results.

Comparison among simulation results and actual

situation measurements show the good behaviour of

the algorithm, the better as the flatter and more

conductive the material is.

As low reflective materials presents reflection paths

in several directions of the incident region,

simulation tools taking into account scattering

patterns instead of just specular reflection will obtain

better predictions.

Figure 16: Scattering patterns, chipwood panel, parallel

polarisation, incidence 20 degree

ACKNOWLEDGEMENTS

This work has been supported by Xunta de Galicia,

Project Ref. PGIDIT05TAM32201PR.

REFERENCES

Arias, A.M., Lorenzo, M.E., Pino, A.G., 1996. A novel

fast algorithm for Physical Optics analysis of single

and dual reflector antennas. IEEE Transactions on

Magnetics.

Beckmann, P., Spizzichino, A., 1963-1987. The scattering

of electromagnetic waves from rough surfaces, Artech

House.

Cuiñas, I., García Sánchez, M., 2000. Building material

characterisation from complex transmissivity

measurements at 5.8 GHz. IEEE Transactions on

Antennas and Propagation, vol.48, pp.1269-1271.

Cuiñas, I., García Sánchez, M., 2001. Measuring,

modeling and characterisation of indoor radio channel

at 5.8 GHz. IEEE Transactions on Vehicular

Technology, vol.50, pp.526-535.

SCATTERING COEFFICIENTS OVER 3-D FLAT DIELECTRIC SURFACES

199