ROUTING IN THE “UMBRELLA” ARCHITECTURE

A. D. Sotiriou, P. Kalliaras, N. Mitrou

School of Electrical and Computer Engineering, Computer Network Laboratory

National Technical University of Athens

9 Heroon Polytechneiou Street, Zographou 15773, Athens, Greece

Keywords: Distributed hash-table, P2P architecture, overlay networks, routing algorithm.

Abstract: Routing in a Peer-to-Peer environment faces a number of challenges, mainly due to its distributed nature. In

this paper we evaluate a new distributed hash table architecture that is able to provide efficient routing

through a fixed-size table. By introducing a set of base algorithms, multiple replication schemas, virtual

nodes and a variable repair mechanism, we are able to ensure successful lookups of published keywords.

Along with theoretical analysis of our proposed work, we present extensive simulation results that testify

and evaluate our protocol.

1 INTRODUCTION

One of the core issues in every network topology is

the routing algorithm applied. This has been

extensively studied and established in constantly

connected networks. However, such algorithms as

OSFP (Moy,1998) require a relevantly good

knowledge of the network topology and assume

constant or almost constant links, at least for a

desired period of time. The introduction however of

ad-hoc and Peer-to-Peer (P2P) networks necessitates

the implementation of new routing strategies that are

able to operate in robust and distributed

environments.

Various solutions have been proposed and there

has been an increasing interest in the adaptation of

distributed hash tables into such networks. Most of

these algorithms are characterized by the size of the

routing table, as this modulates both the algorithms’

efficiency and tolerance to errors. This paper

introduces the Umbrella architecture, a novel routing

scheme based on a distributed hash table of fixed-

size on top of an overlay network. We provide

efficient algorithms for keyword publication and

lookup along with a number of extensions that

improve the system’s tolerability. The key novelty

of our work lies in the fixed-size routing table, as

opposed to other algorithms which are usually

proportional to the network’s size.

The rest of the paper is organized as follows. In

chapter 2 we present related work and ideas that

have been thoroughly studied prior to our

architecture design and in chapter 3 we present our

novel architecture. In the following chapter we

provide in detail the routing algorithms invoked by

our protocol and introduce a number of extensions

that enrich our protocol. Chapter 5 discusses a

number of results obtained through our simulation of

the system and finally, chapter 6 offers useful

conclusions.

2 RELATED WORK

The firsts to introduce routing algorithms that could

be applied to DHT systems were Plaxton, Rajaraman

and Richa (Plaxton,1997). The algorithm wasn’t

developed for P2P systems, and thus every node had

a neighborhood of Ο(logN) and inquires resulted in

Ο(logN) steps. It was based on the ground rule of

comparing one byte at a time until all bytes of the

identifier (or best compromise) were met. A key

feature of their scheme was that the routing table

could be transformed as thus the overlay distance

between nodes could be of a constant factor of the

real distance, when all latencies between nodes are

known. Our scheme meets the logarithmic growth of

inquiries introduced by Plaxton, and even though

nodes are not placed within constant distance from

each other, this is not an issue as it was only

implemented in a theoretical study and not for P2P

environments. A variation of the Plaxton algorithm

was developed by Tapestry (Zhao,2004), properly

adjusted for P2P systems (where overall state is not

available). The algorithm once again tackles one

digit at a time and through a routing table of

234

D. Sotiriou A., Kalliaras P. and Mitrou N. (2006).

ROUTING IN THE “UMBRELLA” ARCHITECTURE.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 234-241

 SciTePress

β*log

N neighbors routes to the appropriate node,

resulting in a search of log

N maximum steps. Our

architecture is based on the fundamentals ideas set

by Plaxton and further developed by Tapestry, but is

also fine-tuned for P2P systems that are likely to

have an enormous amount of population and

content.

Pastry (Rowstron,2001) is similar to Tapestry but

added a leaf set of neighbors that the node first

checks before referring to the routing table. Also a

different neighbor set is maintained for tolerability

issues. Each node maintains a neighborhood of

log

bN rows with (2

-1) elements in each row and

requires a maximum of O(log

bN) steps for enquires.

Proper routing is maintained as long as (L/2) nodes

are available in the neighborhood of each node.

Once again, the variable size of each node’s table

limits the algorithm’s scalability. In addition, our

algorithm’s results showed that inquiries can be

successful even with less available nodes in the

routing table. In Chord (Stoica,2001) a different

approach was applied, placing nodes in a circular

space and maintaining information only for a

number of successor and predecessor nodes through

a finger table. Routing is established through

forwarding queries to the correct successor. Even

though the basic Chord mechanism only requires the

knowledge of one successor, modifications where

needed in order for the system to be applicable to a

robust environment, introducing a finger table of

O(logN) size.

CAN (Ratsanamy,2001) furthered on Pastry’s

alternation and implied DHT in a d-dimensional

Cartesian space based on a d-tore. The space is

constantly divided and distributed amongst nodes,

which must maintain information about their

neighbors and route by following the Cartesian

space. CAN provides a constant O(d) table but,

unlike our algorithm, requires O(dN

1/d

) steps for

lookups. Finally, Kademlia (Maymounkov,2002)

bases nodes in a binary-tree through identifiers.

Each node of the tree retains information concerning

one node from each leaf, other than the one it

resides. It also differentiates by applying an XOR

comparison on identifiers instead of the casual

comparison of each bit, adopted by all other

algorithms. Our algorithm familiarizes with

Kademlia by inserting nodes in a B-tree form, which

is much more versatile and fault-tolerant.

3 ARCHITECTURE OVERVIEW

The proposed architecture is based on the creation of

an overlay network, where all inserting nodes are

identified by a unique code, asserted by applying the

SHA-1 (NIST,1995) hash-function on the

combination of IP and computer name, which

returns an 160-bit identifier. This hash-function has

been proven to distribute keys uniformly in the 160-

bit space and thus provide the desired load balancing

for both the user space and the content space, as the

same function is applied to each content destined for

distribution in the system.

The main objective of the Umbrella architecture

is to insert and retain nodes in a simple and well

structured manner, thus querying and fetching of

content is both efficient and fault-tolerant. In

addition, each node will need only to retain up-to-

date information of a limited, constant number of

neighboring nodes, such allowing the system to

escalate in population of both users and content.

Each node is inserted in the system through an

existing node, which announces the new entrance.

When this procedure has ended successfully, the

new node can, having acquired and informed all

neighboring nodes, continue to publish all of its

content. The publishing procedure is similar to the

insertion mechanism, as content is characterized by

a number of keys, which after being hashed can be

forwarded in the same manner. All keys are

published in an existing node that its identifier is the

closest match to the key identifier. In a similar

fashion, querying is performed by routing the

request to the node with identifier closest to the

desired key.

Figure 1: The Umbrella architecture.

The overlay network is constructed in the form

of a loose B-Tree, where each node is placed in a

hierarchy tree with a parent node and b child nodes.

All nodes are placed along the tree structure, without

being required to fulfil pre-defined ranges as in a

proper B-tree structure, and are responsible for

updating their connections with neighbouring nodes

that reside on either the parent, sibling or child level.

Thus, each node operates autonomously and no

central coordination is needed to maintain the

structure’s integrity. Along with obvious

connections (parent, child and sibling level of each

ROUTING IN THE “UMBRELLA” ARCHITECTURE

235

node), further links to a limited number of nodes in

the near vicinity are kept in record for fault-tolerant

operations. Figure 1 illustrates the structure of this

loose B-Tree. Each level n of the structure is capable

of withholding b

n+1

nodes. Each node has a unique

parent node, which is always one level higher, and a

maximum of b children at a lower level. The

Umbrella overlay network is configured with the

following simple rule. The relation between a parent

node at level n and a child node (which must by

default reside on level n+1) is defined as such and

only such that :

• The n+1 first digits of the parent’s identifier are

equal with the corresponding numbers of the

child’s identifier

• The n+2 digit of the child’s identifier determines

the child’s position in the parent’s child list

The use of a consistent hash function to

distribute identifiers in our node and content space

allows the construction of a well balanced loose B-

tree. The structure becomes even more balanced as

node population increases and nodes fill empty

spaces. The consistent hash function also balances

key distribution among nodes as stated in

(Karger,1997).

As in most DHT systems, a routing table is

maintained by each node in order to route incoming

messages. Each node is responsible for keeping the

table up-to-date by issuing messages to all nodes in

its table at different intervals. The routing table in

our architecture consists of three different sets, a

basic, an upper and a lower set. The basic set stores

nodes and information needed for basic routing

operations under fault-free conditions. The upper

and lower set store additional indexes to nodes in the

upper and lower levels, correspondingly, which are

utilized when nodes in the basic set become

unreachable. These three sets constitute the node’s

neighbourhood table and are presented in Table 1.

Table 1: Fields of the neighborhood table.

Field Set Description

Level Basic The level it resides

Right Basic The non-empty node to the right

Left Basic The non-empty node to the left

Up Basic The parent node

Right2 Upper

The node residing to

the right of the parent node

Left2 Upper

The node residing to the

left of the parent node

Up2 Upper The parent’s parent node

Right3 Lower

One (random) child

of the node to the right

Left3 Lower

One (random) child of

the node to the left

Umbrella Basic All children nodes

Umbrella2 Lower

A (random) child node

from each child

Our architecture’s structure and routing table

described so far ensure that a published key can be

located by an appropriate query within logarithmic

overlay steps to the total size of the network. This is

stated and proved within the following two

theorems:

Theorem 1. Given an Umbrella network of N

nodes with identifiers of base b acquired by a

consistent hash function, the maximum height of the

loose B-tree structure is of logarithmic scale.

Proof : Let b denote the base of our identifiers, N

the total number of nodes and k a particular level in

the Umbrella structure. Then according to the

Umbrella protocol, in each level a maximum of b

nodes can reside, with b

=1 as stated for the first

node that creates the network. Thus, if m denotes the

number of levels required for the above population

of nodes, we acquire, with high probability, the

following relation:

[]

∑

−+−=⇔

⇔

−

bNm

110

1}1)1({log

(1)

Thus the maximum height m of our structure is

of O(log

N). 

Theorem 2. A successful lookup in an Umbrella

network requires with, high probability, O(log

steps.

Proof : Suppose that a node p that resides at level

is seeking for a specific key k that resides within

our network in another node f at level l

. If m

denotes the number of levels of the current network,

N the nodes and b the base of identifiers, then we

could argue that the worst case scenario would

require both nodes to reside at level m and with

maximum distance between them (thus node p is a

m-depth child of the first child at level 0 and on-

forth and node f is the m-depth child of the b child at

level 0 and on-forth). In this case, the lookup must

first ascend all the way to the top of our structure

(thus m steps) and then descend to the bottom (m

steps again). In total, a maximum of 2m steps are

required. Hence, from theorem 1, the required

maximum steps for a successful lookup is, with high

probability, of O(log

N) steps. 

4 ROUTING ALGORITHMS

During the creation of the overlay network, the b

first nodes to enter create the new network by

placing themselves on the top level and forming a

ring. As new nodes arrive, they are placed according

to their identifier. A node only needs to contact an

existing node in the system in order to be inserted

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

236

(mechanisms for fetching existing nodes are not in

the scope of this paper as numerous such techniques

exist (Francis,1999)). Only the first nodes are

automatically inserted regardless of their identifiers;

all subsequent nodes are placed within the system

according to the insertion algorithm. The insertion

mechanism is quite simple and consists of the

following steps:

• Issuing a request on a connected node

• The node checks if the n+1 first digits of its

identifier match, where n is the level it resides

• If not it forwards the message to its parent

• If yes it forwards it to the child with the n+2

digit common with that of the new node

• If such a child does not exist then the new node

is placed as a child to the current node

The publish procedure is similar to insertion and

is therefore suppressed. Conversely, the lookup

mechanism is executed as shown by example in

Figure 2.

Figure 2: Instance of lookup mechanism.

The final mechanism provided by our protocol is

that of voluntary departure from the system and is

given as pseudo-code in Figure 3.

1. delete ( )

if ( has_kids( ) )

rand_kid = choose_random_kid( )

if ( rand_kid.has_kids( ) )

rand_kid.delete( )

else

rand_kid.move_published( )

rand_kid.copy_neighbors( )

inform_neighbors( rand_kind )

10.

disconnect( )

11.

else

12.

this_node.father.move_published( )

13.

inform_neighbors( this_node.father )

14.

disconnect( )

Figure 3: Example for voluntary departure mechanism.

The algorithms presented so far embody the

main mechanisms of our routing protocol and are

capable of maintaining the system stable and fully

functional under normal conditions. The system is

however liable to node departures, either intentional

or due to network disconnections, which we will call

“node failures”. Through changes in the algorithms

already presented we allow the system to bypass

node failures. Most changes are based on using the

upper and lower set of our neighbourhood table to

bypass nodes that aren’t responding. The upper set is

utilized to forward messages to nodes of a higher

level while the lower set for nodes on a lower level.

In the first case, when a node is unable to contact its

parent node it attempts to forward requests

consequently to:

1. the parent’s parent node (Up2)

2. the node to the right of the parent node (Right2)

3. the node to the left of the parent node (Left2)

Whichever of the above succeeds first will

terminate the mechanism. Similarly, the lower set is

utilized for bypassing child node failures. In order to

address the problem of node failures even further,

we have designed a repair mechanism, which is

invoked whenever such a failure is detected. The

algorithm utilizes the voluntary departure algorithm

in order to repair a failure to a child node. It can be

proven that all other failures can be transformed into

a child failure through contacting nodes in the

neighbourhood table and forwarding the repair

message. Once the appropriate node is reached, a

variation of the departure algorithm is evoked in

order to repair the failure by substituting the failed

node with one of its children or by deleting it if none

is available and informing all of its neighbours.

Having presented the core structure and logic

behind our routing protocol, we will continue with a

number of extensions that improve the system’s

performance. The first extension introduces the use

of replication schemas, which has been shown to

increase the robustness of content distribution

systems (Ghodsi,2005). In this paper we have

implemented three additional replication schemas.

We must note that, in contrast with other schemas

found in different protocols, we only replicate

published keywords in nodes and not the actual

content.

Our core routing protocol publishes a keyword in

a single node, the one with closest identifier to that

of the keyword. All three replications schemas retain

this quality and enhance it by also publishing the

keyword to a number of additional nodes, from

which one can recall a successful lookup. Our three

variations are the following:

1. Local Spread Replication (LSR)

The keyword is also published in all nodes

residing in its neighboring table.

2. Inverse Replication (IR)

This mechanism publishes keywords to the

closest match and to the inverse closest match.

3. Local Spread Inverse Replication (LSIR)

It implements a local spread in both the closest

and the inverse closest match.

The second extension implemented allows

nodes to participate in a number of virtual networks,

with a different identifier in each one. This allows

ROUTING IN THE “UMBRELLA” ARCHITECTURE

237

each node to have a different set of neighbours and

thus increase its tolerability substantially. In order to

achieve this, we have defined a number of singular

identifier assignment functions that transform the

original identifiers into a new set of identifiers. This

new set is then used to allocate nodes and route

requests in the virtual networks. We have defined 7

different such functions, which are given below:

1. Inverse Identifier (II)

This function inverses the identifier

2. Inverse per Pair (IP)

The identifier’s digits are inversed by pair

3. Inverse per Pair and Whole (IPW)

All digits are inversed by pair and the result is

inversed as a whole

4. Inverse by Halves (IH)

The II function is applied to the first and second

half of the identifier independently

5. Switch Halves (SH)

The first and second halves are switched

6. Random Reordering (RR)

A random reordering of the identifier’s digits

7. Second Random Reordering (SRR)

Same as RR with different random generator

5 SIMULATION RESULTS

In order to testify our architecture’s integrity and

elaborate on its efficiency we have modeled our

system and its algorithms using the neurogrid

(Joseph,2003) simulator. All of our simulations were

executed on a 3.2MHz PC with 512Mb of RAM and

based on Java.

Prior to our simulation analysis on the efficiency

of our protocol and its performance in general, we

will present the Umbrella topology, as this derives

from the architectural design. For this purpose, we

have used the JUNG (Madadhain,2005) library,

which allows the visual representation of networks.

Once our overlay network has been created and fully

populated, we produce an instance of the network

topology by representing each node (peer) along

with the parent-children pairs of connections. In

addition, we color each node according to the level it

resides, providing an in-sight view of our protocol.

In Figure 4, a number of such instances are given for

different node populations varying from 10 and up

to 1,000 nodes. As can be seen, nodes are spread

along the B-tree structure and although we do not

imply restrictions on the minimum or maximum

number of children for each level (as in a proper B-

tree) the structure is still quite compact.

Figure 4: The Umbrella topology for 10, 100 and 1,000

nodes.

The first part of our initial simulations tested the

basic functionality of the routing protocol under

normal conditions, in other words without the

presence of node failures. All of the results

presented in this set provided 100% success. We

thus present only the number of hops required for a

successful insertion, publish and lookup with a

varying population of nodes. As is seen in Figure 5,

the number of hops grows logarithmically with node

population in all mechanisms. We also notice that

the variance is mainly towards lower number of

hops while higher values are only a fraction larger

than the mean. If we further analyze the results from

the previous figures we will observe that the average

hops required by each operation are given by

2.5*log

N. Thus it satisfies theorem 3 and only

introduces a constant factor of 2.5.

Figure 5: Number of hops for insert publish and lookup

operations.

In the next set of simulations we tested our repair

mechanism in the case of failing nodes in order to

evaluate its effect on the success rate. We conducted

simulations with variant node populations from

1,000 up to 100,000 nodes and periodically issued

random node failures in steps of 10% from 0 up to

80%. An important metric in our repair mechanism

is the rate at which the mechanism is invoked. More

precisely, each node invokes the mechanism in two

cases; either whenever a failure is detected during a

call of one of the protocol’s algorithms or during the

course of a routing table consistency check, which is

issued periodically by each node. The former is

constant and issued throughout our simulations,

while the latter varies as we have conducted

simulations with different consistency check

periods. In the results presented here we have varied

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

238

this period and executed simulations for period times

10T and 20T, where T is a constant representing

communication activity of each node (in our case T

equals to 100 messages), ensuring that an inactive

node will not suffocate the network with repair

messages.

Figure 6: Successful lookups as a function of failures

without and with repair 10T.

Firstly we investigate the impact of the repair

mechanism on the success rate of lookup operations.

As seen in Figure 6 the repair mechanism

dramatically increases the success rate regardless of

the node population and the check period. The

protocol is able to produce linear deduction of the

successful lookup rate as opposed to the logarithmic

decrease observed without the repair mechanism.

The impact of the repair mechanism is better

observed in Figure 7, where we have mapped the

success rate of lookups against node failures for the

case of 100,000 nodes, for no repair, repair period

10T and 20T. The results were dramatically

improved in both cases where the repair mechanism

was applied. The results obtained with repair period

10T are a fraction higher than those of 20T, which

was expected as nodes check their routing table’s

consistency less frequently.

Figure 7: Successful lookup for no-repair, 10T and 20T

repair.

In the second set of simulations we applied our

two protocol extensions, the replication schemas and

the virtual networks. We will present the effect of

each extension and evaluate the overall protocol

efficiency when all variations are applied.

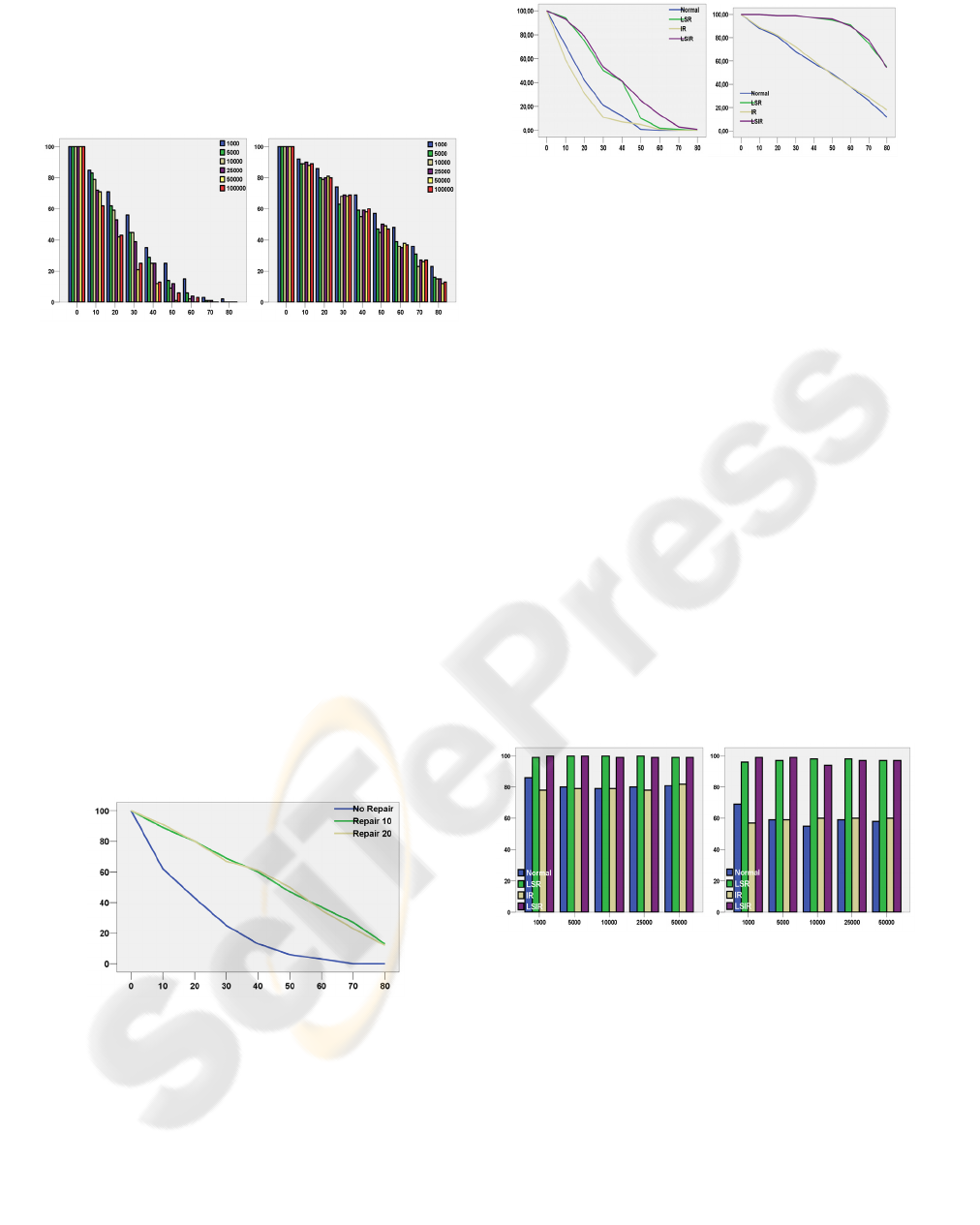
Figure 8: Lookup success ratio for different replication

schemas and repair periods.

Firstly we will evaluate the effect of the different

replication schemas to the efficiency and tolerability

of our routing protocol. In our simulations, we

varied the node population from 1,000 up to 50,000

nodes and generated failures in steps of 10% from 0

up to 80%. In the first diagram of Figure 8 we have

sketched the successful lookup ratio as the node

failure ratio increases, for a network of 50,000 nodes

and varying replication schemas and repair periods.

We observe that while the inverse replication (IR)

schema does not better the protocol’s efficiency,

both the local spread replication (LSR) and the local

spread inverse replication (LSIR) schemas improve

the protocol’s success rate vastly. These

improvements are even more significant when the

repair mechanism is applied, as seen in the second

diagram of Figure 8. The protocol is able to sustain

100% success rates up to 30% fail rates when a

repair period of 10T and either LSR or LSIR

schemas are applied. Moreover, success rates higher

than 80% are achieved for up to 70% fail rates when

a 10T repair period is applied and a LSR or LSIR

replication schema is implemented.

Figure 9: Lookup success ratios for different replication

schemas and failure ratios.

In the next figure, Figure 9, we can see the

impact of node population on the combination of

replication schemas. We have controlled the repair

period and retained it constant and equal to 10T and

varied the failure ratio between 20% and 60% for the

four different replication schemas and for node

populations of 1,000 up to 50,000. As can be seen,

the node population does not affect the success rate

for any replication schema or failure ratio. This

ROUTING IN THE “UMBRELLA” ARCHITECTURE

239

shows that our protocol can escalate and support

intense node populations.

Figure 10: Per node messages for different replication

schemas as a function of node population.

Finally we investigated the drawback of the

proposed replication schemas. As can be seen from

Figure 10 the new schemas incur an increase in the

number of messages exchanged between peers. The

use of the IR schema doubles the number of

messages required while the LSR and LSIR induce

an increase by a factor of 2.5 and 6.0 respectively.

Even though these changes may sound significant

they are actually quite efficient since even in the

case of 50,000 nodes and LSIR replication schema

the total does not exceed that of 45 messages for the

whole duration of the simulation.

Figure 11: Average of successful lookups for varying

virtual networks as a function of node population.

In our final series of simulations we will try to

evaluate the effect of the virtual networks extension.

During this analysis, in many cases, we present

aggregated results due to the multiple variables that

affect each simulation. All presented results evaluate

the case of having 1 (no virtual networks), 2 , 4 or 8

virtual networks. In Figure 11 the average of

successful lookups is shown for varying virtual

networks as a function of node population. The

average derives from the aggregation of all

combinations of replication schemas, repair periods

and failing ratios. With that in mind, we must point

out that the optimum success rate for our protocol is

much higher than the average shown in this figure.

However, the average presents an indication of the

virtual networks’ effect on the success rate. It is

clear form the data on the figure that as the number

of virtual networks increases the success rate

improves tremendously, and from an average of

around 65% for no virtual networks it raises to 75%,

85% and 90% for the cases of 2, 4 and 8

respectively. This is further testified by observing in

Figure 12 how virtual networks affect the success

rate for different replication schemas. Once again,

the success rate increases linearly with the number

of virtual networks, for all replication schemas.

Figure 12: Average of successful lookups for varying

replication schemas as a function of virtual networks.

Having established the beneficial effect of the virtual

networks extension, we will now present the

optimum protocol performance. In Figure 13 we

seek the optimum performance of our protocol. We

vary the number of virtual networks between 1 and 8

and the repair period between 0 and 10T, for the

average of all replication schemas. As can be seen,

Table 2: Success rates for combinations of virtual networks, repair periods and replication schemas per node failure ratio.

Network 2 4 8

Repair 10T 20T 10T 20T 10T 20T

Replication LSR LSIR LSR LSIR LSR LSIR LSR LSIR LSR LSIR LSR LSIR

100 100 100 100 100 100 100 100 100 100 100 100

100 100 99 99 100 100 100 100 100 100 100 100

100 100 99 100 100 100 100 100 100 100 100 100

99 100 99 99 100 100 100 100 100 100 100 100

99 99 98 99 100 100 100 100 100 100 100 100

96 97 93 97 99 100 96 99 100 100 96 100

Failure %

73 86 67 77 98 98 82 97 98 99 97 99

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

240

for the case of 8 virtual networks, a 100%

mechanism, while this rate increases up to 80%

when a 10T repair period is applied. In the latter

case, even with 4 virtual networks an optimum

performance is achieved for up to 60-70% node

failures.

Figure 13: Success rate for different combinations of

virtual networks and repair period as a function of failures.

Finally we will present some conclusive results

for the optimum performance of our protocol. In

Table 2

we can see the success rates for the best

combinations of virtual networks, replication

schemas and repair periods as node failures increase.

For all combinations, the protocol routes

seamlessly when node failures don’t exceed a 40-

50% ratio. If we want our protocol to tolerate even

more node failures then either 4 or 8 virtual

networks should be implemented, regardless of the

check period or the replication schema. Here we

point out that the repair mechanism is a pre-

requirement, in contrast to the repair period, which

can be relaxed to 20T without significant loss in

performance. The same applies for the replication

schema; the LSR schema must be at least applied but

the LSIR is not vital as results are only slightly

better.

6 CONCLUSIONS

Through the course of this paper we presented the

Umbrella protocol; a novel protocol based on a

distributed hash table that supports key publishing

and retrieval on top of an overlay network for

content distribution. We have analysed our protocol

and its algorithms through both theoretical and

simulation means and proved its corrective ness and

efficacy. Its main novelty lies in its fixed-size

routing table sustained by each node, which is able

to provide efficient routing even under contrary

conditions. The protocol has also proved to be

scalable due to its low traffic load demands. The

results obtained by our simulations proved that the

protocol, along with a number of valuable

extensions, is able to route seamlessly successful

lookups in O(log

N) steps even when more than

80% of the system’s population suddenly fails.

REFERENCES

Francis, P. (1999). “Yoid : Extending the Multicast

Internet Architecture,” White paper,

http://www.aciri.org/yoid

Ghodsi, A., Alima, L.,O., Haridi, S. (2005). “Symmetric

Replication for Structured Peer-to-Peer Systems”, The

3rd International Workshop on Databases, Information

Systems and Peer-to-Peer Computing, Trondheim,

Norway , August

Joseph, S. (2003). “An Extendible Open Source P2P

Simulator,” P2PJournal

Karger, D., Lehman, E., Leighton, F., Levine, M., Lewin,

D., Panigrahy, R. (1997). “Consistent hashing and

random trees: Distributed caching protocols for

relieving hot spots on the World Wide Web”, in

Proceedings of the 29

Annual ACM Symposium on

Theory of Computing, El Paso, TX

Madadhain J., Fisher D., Smyth P., White S., Boey Y.

(2005). “Analysis and Visualization of Network Data

using JUNG”, http://jung.sourceforge.net

Maymounkov, P., Mazieres, D. (2002). “Kademlia: A

peerto -peer informatic system based on the XOR

metric,” in Proceedings of IPTPS'02, (Cambridge,

MA)

Moy J. (1998). “OSPF Version 2”, Network Working

Group, RFC 2328

National Institute of Standards and Technology. (1995).

“FIPS Pub 180-1: Secure Hash Standard (SHA-1),”

Federal Information Processing Standards Publication

Plaxton, G., Rajaraman, R., Richa, A.W. (1997).

“Accessing Nearby Copies of Replicated Objects in a

Distributed Environment,” in 9th Annual ACM

Symposium on Parallel Algorithms and Architectures

(SPAA)

Ratsanamy, S., Francis, P., Handley, M., Karp, R. (2001).

“A scalable content-addressable network,” in ACM

SIGCOMM Conference, ACM Press, San Diego (CA)

Rowstron, A., Druschel, P. (2001). “Pastry: Scalable,

decentralized object location, and routing for large-

scale Peer-to-Peer systems,” in Middleware 2001

Stoica, I., Morris, R., Karger, D., Kaashoek, F.,

Balakrishnan, H. (2001). “Chord: A Peer-to-Peer

Lookup Service for Internet Applications,” in Proc.

SIGCOMM

Zhao, B. Y., Huang, L., Stribling, J., Rhea, S.C.,

Joseph,A.D., Kubiatowicz, J.D. (2004). “Tapestry: A

resilient global-scale overlay for service deployment,”

IEEE Journal on Selected Areas in Communications

ROUTING IN THE “UMBRELLA” ARCHITECTURE

241