
HIERARCHICAL AND PSEUDO-RANDOM EIRA CODES BASED
ON BIBDS AND PRIMITIVE INTERLEAVERS
Jesús Miguel Pérez Llano, Víctor Fernández Solórzano
Microelectronics Engineering Group TEISA, ETSIIyT,Cantabria University, Av. Los Castros, Santander, Spain
Keywords: LDPC, eIRA, DVB-S2, BIBD, error floor.
Abstract: This paper describes a method based on hierarchical matrices and primitive generators that allows low cost
coder and decoder implementations. The hierarchical approach is well suited for decoder implementation
and, in addition, the method has been applied to eIRA structures which have demonstrated a reduced coder
implementation complexity. Despite the added structure to eIRA original codes, the architecture presented
shows similar BER performance. To achieve this, BIBDs have been used to avoid length-four cycles and
primimitive generators contribute to get a pseudo-random construction. Moreover, the reduction of low
weight codewords and near codewords are considered in order to reduce error-floors.
1 INTRODUCTION
Although LDPC codes (Gallager, 1962)(Mackay,
1999) have been well known in research for a long
time, they have reached the “standard world”
through standards such as IEEE 802, some NASA
standards and DVB in the recent DVB-S2 standard
(DVB-S2, 2004). LDPC capabilities led to them
being adopted for the previously mentioned
standards: on the one hand because they are easier to
decode than well known Turbo Code based systems
and with more flexible architectures, and on the
other hand because of their BER performance.
Moreover, their implementation throughput makes
them an efficient architecture-aware channel coding
scheme.
In spite of all these advantages, LDPCs have
some disadvantages from the point of view of
hardware design whose effects are worth mitigating
(if the BER performance is not greatly affected).
Randomly designed LDPCs (Mackay, 1997) have
been demonstrated to have superior BER
performance. However, their implementation cost
becomes unviable when the parity matrix size
increases. Moreover, the codification of this kind of
code generally becomes non sparse.
This work has been supported by the Spanish MEC through the
TEC2005-03301 project.
Some alternatives have been proposed to avoid
the aforementioned implementation difficulties.
Finite Geometry based LDPCs (Kou, 2001) have a
greatly simplified codification but in general their
matrices are regular and very dense, which makes
their implementation cost a relevant drawback.
In (Yang, 2004) a new class of LDPCs called
eIRAs was recently shown to have a simplified
codification scheme, with good BER performance.
Their biggest flaw is that a considerable part of its
structure remains random (with the problems
previously alluded to).
The implementation proposed in this paper is
based on hierarchical matrices, which have been
demonstrated, in (Mansour, 2003)(Mansour, 2004)
by Mansour and in (Liao, 2004) by Liao and Yeo, to
be suitable for decoder implementation. Mansour
suggests the use of well known architectures such as
Ramanujan (Rosenthal, 2000) or cyclotomic sets
(Mansour, 2002) which have good structural
properties but with some weaknesses, as the error
floor due to low weight codewords (Mackay, 2003)
and the lack of flexibility (Zhang, 2004). Liao and
Yeo propose a completely random top and bottom
architecture that do not ensure the absence of length-
four cycles which has been demonstrated to have an
important influence on BER. In contrast, the basis of
our design is a well defined architecture based on a
BIBD (Ammar, 2004)(Ammar, 2002) design at the
top level architecture -which avoids length-four
cycles- and pseudo random permutations with
151
Miguel P
´
erez Llano J. and Fern
´
andez Sol
´
orzano V. (2006).
HIERARCHICAL AND PSEUDO-RANDOM EIRA CODES BASED ON BIBDS AND PRIMITIVE INTERLEAVERS.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 151-157
Copyright
c
SciTePress
optimal roots at the bottom level designed to avoid
low weight codewords and near codewords
following recommendations of (Yang, 2004)(Dinoi,
2005)(Tian, 2004). Moreover, our proposal not only
reduces the complexity of the decoder, as previously
mentioned works do, but it simplifies the coder
complexity.
The use of primitive generators (Morelos-
Zaragoza, 2002) for the bottom level matrices
enables the implementation presented to avoid
storing the pointers, necessary to locate the 1’s in the
parity check matrix (the only pointers to be stored
are those that define the BIBD structure which
require much less memory consumption) without
losing randomness.
The approach presented outperforms the
congruent sequences based LDPCs (Prabhakar,
2002), which avoid the memory for the pointers but
are more restrictive, being regular and only defining
a bit degree of 3 in contrast to the architecture
presented which is much more flexible.
The use of eIRA codes provides our design with
a high performance from the point of view of BER.
Moreover, the absence of cycles 4 combined with
the optimal distribution of the connections in the
parity matrix lead to minimize low weight
codewords and near codewords, thus lowering the
error floor. In Section II the architecture proposed
will be discussed. In section III the BER
performance of the scheme is presented. Finally, in
chapter IV, the conclusions of this paper are
presented.
2 ARCHITECTURE PROPOSED
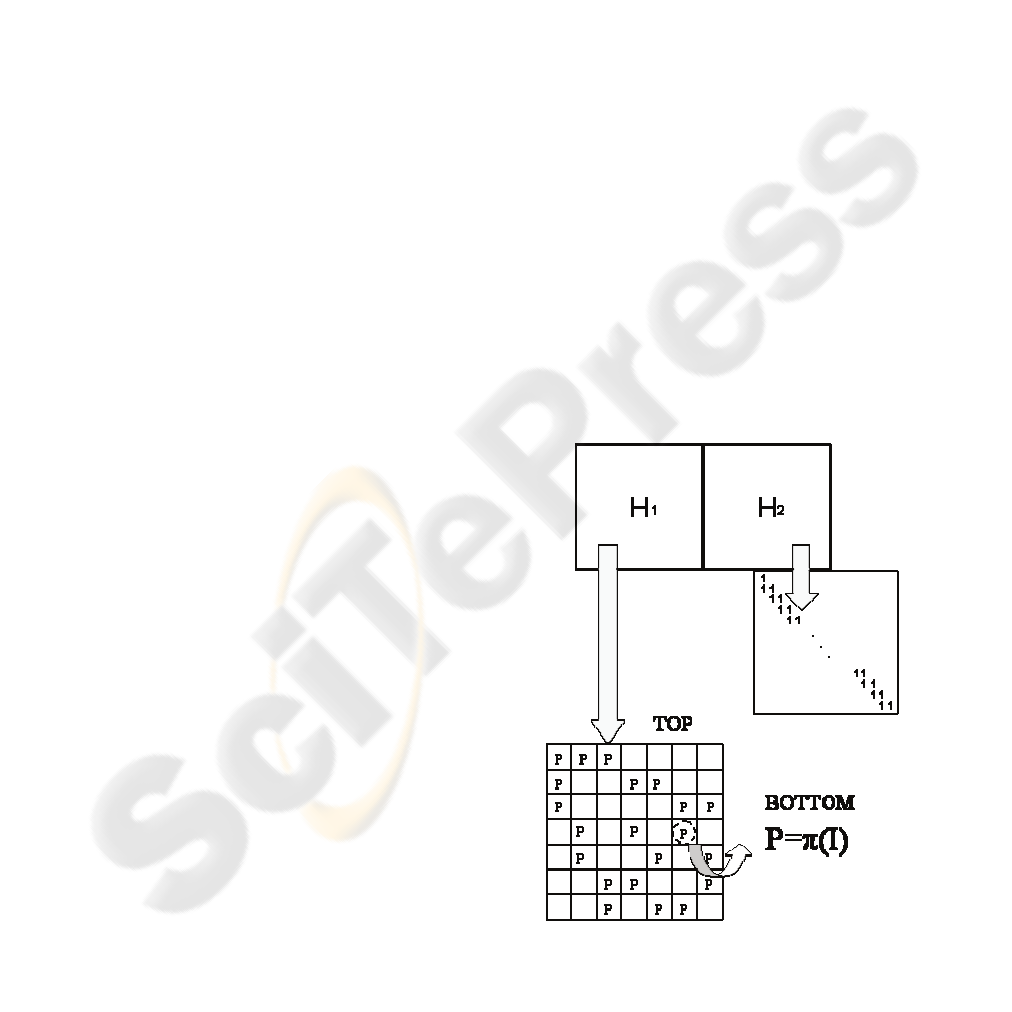
LDPCs based on eIRAs (Yang, 2004) are
constructed dividing the parity check matrix into two
parts called H
1
and H
2
. H
2
is defined as a square
matrix of size m (where m is the number of parity
bits) composed of m-1 degree-2 columns and one
degree-1 column (see Figure 1). In contrast, H
1
does
not have a defined architecture, being designed at
random (avoiding length-four cycles by removing
appropriate bits) in (Yang, 2004).
In the architecture proposed H
1
is divided into
several smaller matrices which are permutations of
the identity matrix or square zero matrices (see
Figure 1).
The TOP level architecture of H
1
will be chosen
to avoid length-four cycles using the BIBD structure
as will be explained in II-A. The sub-matrices,
which are permutations of the identity matrix, are
called permutation matrices and their structure and
construction will be shown in II-B. The absence of
length-four cycles in TOP level architecture ensures
a length-four cycle free parity check matrix because
sub-matrices have no more than one ‘1’ per column.
The architecture proposed is independent of the
frame size and only depends on the bit degree and
rate. To obtain different sizes the only thing that
needs to be modified in the design is the size of
bottom matrices, keeping the top matrix unchanged.
Bearing in mind that positions to be stored are those
of the top matrix, as code size increases, the
architecture proposed needs relatively less memory
than classical approaches.
2.1 TOP Level Architecture
The importance of avoiding cycles of length 4, for
BER performance of LDPC based codes, has been
widely demonstrated (Tian, 2004)(Mao, 2001). With
this idea in mind, the design presented develops a
way to design parity check matrices distributing the
permutation matrices in such a way that they do not
form length-four cycles. Moreover, this method can
be used with various matrix sizes and rates.
The approach presented makes use of BIBDs
(Balanced Incomplete Block Designs) (Anderson,
1990) in order to achieve a length-four cycle free
matrix with minimum dimension for a given bit
degree. BIBDs combine a number of points to form
Figure 1: Proposed eIRA parity check matrix.
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
152

groups. They are defined by -at least- three
parameters called v, r, λ, where v is the total number
of points, r is the number of blocks which a point is
in (i.e. the bit degree in LDPC terms) and λ defines
the number of blocks in which each pair of points
are together. Translating these parameters to the
matrix field, v represents the number of columns, r is
the number of 1’s per column and λ=1 will
determine the absence of length-four cycles: a value
of 1 ensures that any pair of 1’s will be in only one
row.
The BIBD-based matrices chosen are rate 1/2
matrices, so, for rate 1/2 the construction is
immediate, turning the BIBD into a matrix. There
are several possibilities for BIBDs with λ=1. The
most well known are affine planes and projective
planes. The latter will be used in our designs
because their total number of points is less than that
needed in affine planes for a given maximum degree
of parity matrix. Using fewer points allows us to use
bigger permutation matrices, which leads to better
BER performance and which also needs fewer
memory elements in implementation.
The parameters that define projective planes are:
(n
2
+n+1, n+1, 1). For example, Figure 1 shows a
BIBD(7,3,1). The way the matrix rows defined by
the BIBD are arranged should be noted.
In order to get rates lower than 1/2 the BIBD to
be used is the same as the one used for 1/2, chosen
to satisfy the optimal bit and check degree. The only
difference is that once the top matrix has been
defined, some columns are removed to adjust the
rate.
For rates higher than 1/2 the process proposed
consists in removing some rows of the original
matrix. An example can be seen in section II-C.
The number of memories used to store
information bits depends on the parallelism desired.
If a high parallelism is desired, the number required
to implement a BIBD with high rate (the highest
parallelism is obtained using a memory for any
column of the top matrix) can be a drawback for
designers. For example, for a bit degree of 13 the
system would require 157 memories.
In order to offer an alternative solution to this
problem, another option is proposed. Depending on
the bit degree desired a BIBD with a suitable
number of elements per column is chosen.
Moreover, depending on the rate to be reached,
either the whole BIBD or only a part of it (this last
option allows higher rates) is used. After that, the
resulting BIBD is cloned and put side by side with
itself. The only difference between both parts is the
way their pseudo-random primitive generators are
designed. The primitive generators of the BIBD on
the right are exactly the same as their equivalents on
the left, but the init_value (explained in the next
section) is changed depending on the row. This
ensures that the new structure is still length-four
cycle free with the bit degree desired and high rate.
In sub-section II-C an example of design is
explained.
Although all the proposed schemes define semi-
regular eIRAs (H
1
been regular), the method
proposed is flexible and irregular eIRAs can be
obtained by removing permutation matrices in top
level architecture in columns where degree should
be reduced.
2.2 BOTTOM Level Architecture
Once all the sub-matrices have been emplaced using
BIBDs, the way the permutation of the identity
matrix is defined will be explained. The objective of
primitive generators will be to produce the pointers
to the systematic bits needed to generate a given
parity bit.
Obviously, a completely random generator
cannot be implemented. The proposed method is
based on primitive interleavers (we will call them
primitive generators) (Morelos-Zaragoza, 2002).
These interleavers have the desirable property of
being very simple to design, fast and with low area
cost and, from the point of view of BER
performance, they perform only slightly worse than
a completely random one in this kind of systems.
The interleaved positions are calculated through the
following equation:
(
)
Nrootii
kk
mod
1
+
=
+
(1)
There are three parameters that define the
pseudo-random sequence, N (the maximum value,
and the total number of values where the sequence is
complete), the init_value (the initial value i
0
) and the
root (the difference between one value and the next
or previous one). How these parameters will be
chosen is important in the BER performance of the
system.
The proposed design suggests an N which is
prime. This fact allows the use of as many different
roots as N-1 (a valid root is a root that forms
complete N sequences). Moreover, N is chosen to
satisfy:
numbercolumnNframesize _*≈
.
Fortunately, despite this restriction, there are enough
prime numbers and so widely distributed that any
frame size can be approximated.
HIERARCHICAL AND PSEUDO-RANDOM EIRA CODES BASED ON BIBDS AND PRIMITIVE INTERLEAVERS
153
The idea of having several roots increments the
randomness of the whole parity check matrix
because despite using the same generator the
sequences obtained are different. On the other hand,
following recommendations in (Yang, 2004)(Dinoi,
2005)(Tian, 2004), in order to reduce low-weight
codewords and near codewords, for lower degree
variables, which are mainly responsible of error
floors, roots are selected so that ones of columns and
pairs of columns are widely separated. This is done
by using an algorithm that performs two steps:
1.- For a given bit degree distribution, the initial
BIBD has a column degree which is equal to
maximum bit degree. Lower degrees are obtained by
removing column elements. This elimination is
performed in columns whose elements are less
distributed.
2.-Once the optimal degree is obtained, the
algorithm chooses the optimal roots for the lowest
weight columns. These optimal roots will be chosen
to maximize the average distance between elements
within any two columns as well as in any column
itself.
Moreover, the chosen root is also used as
init_value in order to begin at a different number for
any sub-matrix. Roots selected with the mentioned
methodology will be called distributed roots in the
next results section.
Using the above recommendations the BER
performance of the system is close to that obtained
using a completely random generator.
2.3 Example of Code Construction
To clarify the proposed method a simple example
will be discussed. We will describe the design
process for three different rates.
Rate 1/2: Suppose a rate 0.5 eIRA with column
degree 3. With only these requirements the design is
as easy as choosing a BIBD (7,3,1). Figure 2
displays the TOP matrix, which is clearly length-
four cycle free.
Figure 2: BIBD(7,3,1) for H
1
of rate 0.5 eIRA.
Figure 3: H
1
of rate 0.6 eIRA.
The next step would be to define the primitive
generator parameters for the required generators, in
the way that has been defined in II-B.
Rate 0.6: to obtain a slightly higher rate, the
same BIBD shown in Figure 2 can be used. This
time only four of its rows are to be used. If rows
1,2,4 and 7 are used and the last column is removed,
a 0.6 rate eIRA code is obtained (with a degree of 2
for any bit in H
1
). The matrix mentioned can be seen
in Figure 3. Of course, depending on the degree
needed the user can define which rows are used and
can even add or remove columns or P’s (while the
length-four cycle free structure is maintained). The
initial BIBD defines the maximum degree available,
so if a bigger degree is needed, another BIBD, with
bigger r, has to be chosen.
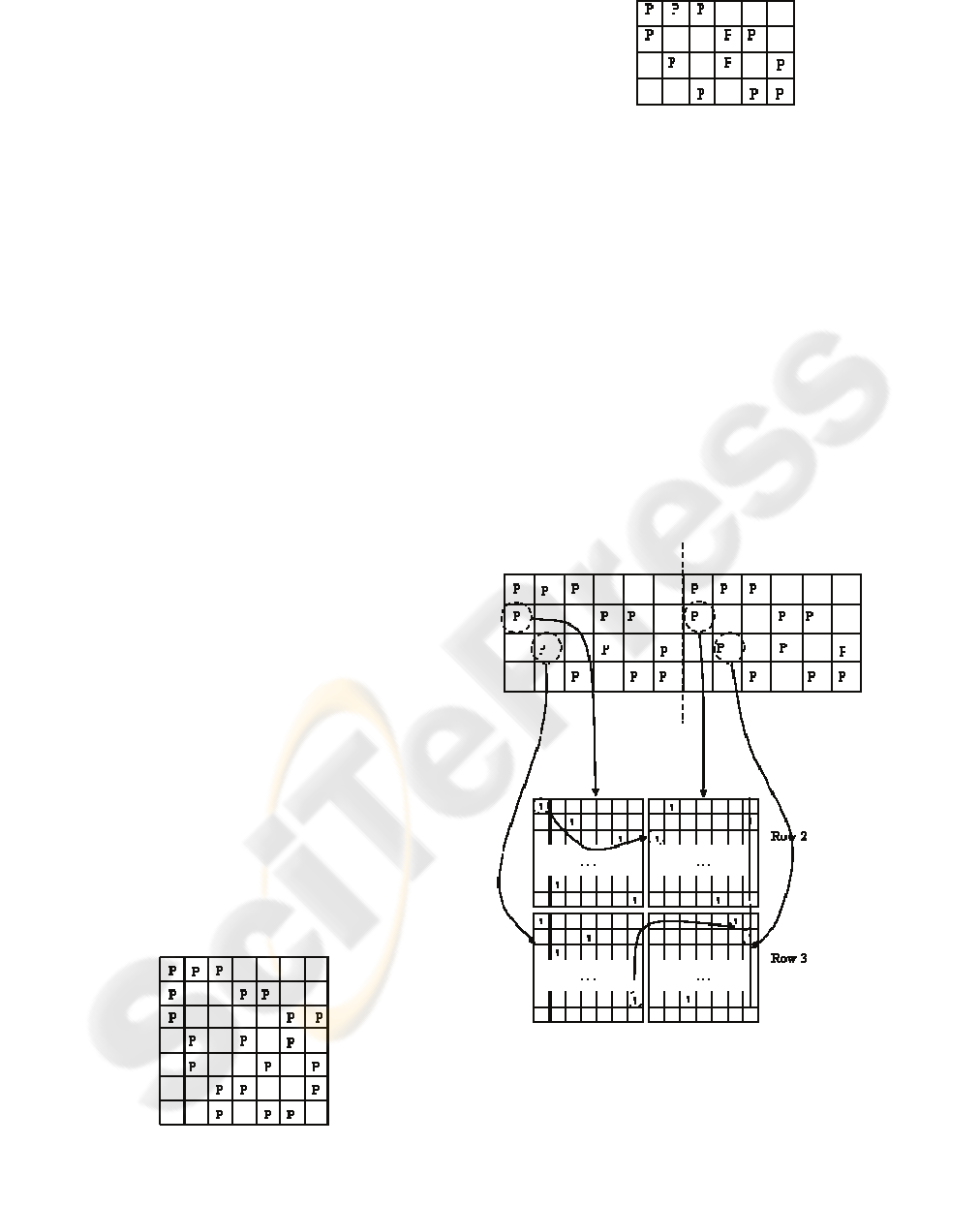
Figure 4: (a) H1 of rate 0.75 eIRA (b) Bottom level
architecture detail for 2P matrices on the left TOP level
matrix and their corresponding matrices on the right.
Rate 0.75: the last example will achieve a 0.75
rate eIRA maintaining the degree of 2 for any bit. At
(a)
(b)
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
154

this point there are two possibilities as was
explained previously: on the one hand, a suitable
BIBD can be used, removing rows till the rate
desired is obtained. On the other hand, the
architecture explained in II-A can be used, i.e.,
choosing a smaller BIBD and cloning it to form a
TOP architecture with higher rate.
For this example the second alternative is
applied, using the original BIBD(7,3,1) matrix. To
do so, the matrix in Figure 3 will be cloned. The
primitive generator used on the left is designed in
the same way as in the case of low rate. The
primitive generator used on the right of the dotted
line in Figure 4-a has as its init_value the row in
which that generator is placed. With this simple idea
a length-four cycle free parity check matrix is
obtained in spite of having length-four cycles in the
TOP architecture.
The top level architecture defined in this way is
displayed in Figure 4-a and a bottom level detail for
two generic square P matrices is shown in Figure 4-
b.
3 BER PERFORMANCE
The results obtained in the original eIRA paper
(Yang, 2004) will be taken as the main point of
reference. The same two rates and frame sizes
reported in this paper have been tested with our
methodology. Moreover, the same bit and check
degrees will be used too, because they have been
demonstrated to be optimal using Gaussian
approximation (Richardson, 2001). The Mansour
(Mansour, 2003) results will also be compared but
not forgetting that it is not an eIRA approach.
3.1 Rate 0.5
For the rate 0.5 example in (Yang, 2004), the frame
size used (4018, 2009) is approximately the same as
the one reported there (4000, 2000). The reason for
the slight frame size difference is the use of a prime
N and a BIBD (49, 7, 1). In this particular case, N
was set to 41 as this is the prime value that provides
the frame length closest to the desired one: 41 x 49 =
2009.
We began using the same check and bit degrees
as the original eIRA because they have been
demonstrated to be optimal using differential
evolution. The proposed bit degree for H
1
matrix
was 58% of information bits with degree 3 and 42%
with degree 7. On the other hand roots of primitive
generators were randomly elected. Results can be
seen in Figure 5 labeled as eIRA BIBD (58%w3,
42%w7, rr) where rr means random roots.
Performance is clearly improved selecting roots
following the previously mentioned criteria, based
on separating widely the ones on columns and pair
of columns. The use of these distributed roots and its
BER performance is labeled as eIRA BIBD (58%w3,
0%w4, 42%w7, dr) , where dr means distributed
roots, in Figure 5.
The next step to improve the BER performance
in the error floor zone was to increase top level
columns to degree-4. A top level column is a column
of the top level matrix, which contains 41
information bits in this particular case. In order to
low the error floor a method based on increasing the
top level columns that are involved in most low
weight codewords and near codewords is proposed.
Basically the method consist in studying the quantity
of errors in which each top level column is involved
in and increase the degree of those with most errors
(Pérez, 2005).
Increasing 3 top level columns (3*41
information bits), which constitutes 6% of the total
number of columns, the BER performance in the
error floor zone (SNR=1.6dB) is improved from
2*10
-5
to 9*10
-6
. Finally, by increasing 6 top level
columns (12% of the weight 3 columns) the BER
performance goes below 3*10
-6
as can be seen in
Figure 5.
Final results are labeled as BIBD (46%w3,
12%w4, 42%w7, dr) in Figure 5, indicating the
percentage of columns increased to degree-4. This
final result can also be seen in Figure 6, compared to
the original eIRA results presented in (Yang, 2004).
As can be observed, the proposed method is really
close to the original eIRA in terms of BER
performance, but eliminating the random topology
of the parity check matrix with the implementation
benefits this feature implies.
1,00E- 06
1,00E- 05
1,00E- 04
1,00E- 03
1,00E- 02
1,00E- 01
0,8 0,9 1 1,1 1,2 1,3 1,4 1,5 1,6
Eb/ No
BE
R
eIRA BIBD (58%w3, 0%w4, 42%w7, dr)
eIRA BIBD (52%w3, 6%w4, 42%w7, dr)
eIRA BIBD (46%w3, 12%w4, 42%w7, dr)
eIRA BIBD (58%w3, 42%w7, rr)
Figure 5: Influence of the percentage of weight 4 columns
in BER performance.
HIERARCHICAL AND PSEUDO-RANDOM EIRA CODES BASED ON BIBDS AND PRIMITIVE INTERLEAVERS
155

3.2 Rate 0.8
For this scheme, the frame size was a little bigger
(4495, 3534) than the one used in (Yang, 2004)
(4161, 3430). Moreover, the rate is a little smaller
(0.786 instead of 0.82). These two small differences
can explain the performance of our system being
almost 0.2dB better than the original one (using the
same check and node degrees) as can be seen in
Figure 7. Anyway, the difference is minimal and the
performance is as close to the (Yang, 2004) design
as expected.
Finally we present a comparison between Mansour
(Mansour, 2003) design, a random regular design
also reported in (Mansour, 2003) and our proposal
for rate 0.5 and frame size (1008). In (Mansour,
2003) the degree used by Mansour was not
specified.
1,00E-06
1,00E-05
1,00E-04
1,00E-03
1,00E-02
1,00E-01
1,00E+00
0,8 0,9 1 1,1 1,2 1,3 1,4 1,5 1,6
Eb/ No
BE
R
eIRA original
eIRA BIBD(46% w3, 12% w4, 42% w7, distributed )
Figure 6: Performance comparison of original and
proposed n≈4000 rate-0.5 eIRAs.
1,00E-06
1,00E-05
1,00E-04
1,00E-03
1,00E-02
1,00E-01
1,00E+00
2,2 2,4 2,6 2,8 3 3,2 3,4
Eb/No
BER
eIRA original of length 4161 and rate 0.82
eIRA BIBD of length 4495 and rate 0.786
Figure 7: Performance comparison of original and
proposed n≈4000 rate-0.8 eIRAs.
1, 0 0 E - 0 6
1, 0 0 E - 0 5
1, 0 0 E - 0 4
1, 0 0 E - 0 3
1, 0 0 E - 0 2
1, 0 0 E - 0 1
1,00E+00
1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6 2,8
Eb/ No
BE
R
Random c ode with no 4- cycles of length 1008, rate 0.5
Mansour LDPC code with AA-structure of length 1008, rate 0.5
eIRA BIBD distributed roots of length 1008, rate 0.5
Figure 8: Performance comparison of various n≈1000
rate-0.5 regular LDPC codes.
In this paper the optimal degree calculated via the
density function for this rate and size has been used.
Comparison can be seen in Figure 8. Our design
outperforms both the Mansour and random designs
by approximately 0.2 dB.
4 CONCLUSIONS
In this paper a new architecture for designing eIRAs
is proposed. A design based on hierarchical matrices
is proposed, combining the deterministic structure of
BIBD (x, y, 1) designs, avoiding length-four cycles,
with the good BER properties of pseudo-random
constructions in order to create a hardware-aware
design which allows high parallelism with BER
performance close to the eIRAs theoretical
performance. Moreover, with the method defined in
this paper we are able to improve BER performance
and error floor by distributing the elements of H
matrix and by selectively increasing bit degrees.
REFERENCES
Gallager, R. G., 1962. Low-density parity-check codes. In
IRE Transactions in Information Theory, vol. IT-8,
pp.21-28.
MacKay, D. J. C., 1999. Good error-correcting codes
based on very sparse matrices. In IEEE Transactions
on Information Theory, vol. 45, pp. 339-431.
DVB-S2 Standard, 2004: EN 302 3027 v1.1.1.
MacKay, D. J. C. and Neal R. M., 1997. Near Shannon
limit performance of low density parity check codes.
In Electronic Letters, vol. 33, no. 6, pp.457-458.
Kou, Y., Lin, S. and Fossorier M. P. C., 2001. Low-
density parity-check codes based on finite geometries:
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
156

A rediscovery and new results. In IEEE Transactions
on Information Theory, vol. 47, pp. 2711-2736.
Yang, M., Ryan, W. E. and Li, Y., 2004. Design of
Efficiently-Encodable Moderate-Length High-Rate
Irregular LDPC Codes. In IEEE Transactions on
communications., vol. 52, pp.564-571.
Mansour, M. and Shanbhag, N., 2003. High-throughput
LDPC decoders. In IEEE Transactions on VLSI
Systems., pp.976-996.
Mansour, M., 2004. High-Performance Decoders for
Regular and Irregular Repeat-Accumulate Codes. In
Proceedings IEEE GlobeCOM, Dallas, USA.
Liao, E., Yeo, E. and Nikolic, B., 2004. Low-density
parity-check code constructions for hardware
implementation. In Proceedings IEEE ICC, Paris,
France.
Rosenthal J. and Vontobel P.O., 2000. Constructions of
LDPC Codes Using Ramanujan graphs and Ideas for
Margullis. In Proceedings of the 38-th Allerton
Conference on Communications, Control and
Computing, Illinois, USA.
Mansour, M. and Shanbhag, N., 2002. Low Power VLSI
Decoder Architectures for LDPC Codes. In
Proceedings ISLPED.
MacKay, D. J. C and Postol, M. S., 2003. Weaknesses of
Margulis and Ramanujan-Margulis low-density parity-
check codes. In Electronic Notes in Theoretical
Computer Science.
Zhang, T. and Parhi, K. K., 2004. Joint (3,k)-Regular
LDPC Code and Decoder/Encoder Design. In IEEE
Transactions on Signal Proccesing, vol. 52, no. 4, pp.
1065-1079.
Ammar, B., Honary, B., Kou, Y., Xu, J., and Lin, S., 2004.
Construction of Low Density Parity Check Codes
based on balance incomplete block designs. In IEEE
Transactions on Information Theory.
Ammar, B., Honary, B., Kou, Y., and Lin, S., 2002.
Construction of Low Density Parity Check Codes: A
Combinatoric Design Approach. In Proceedings IEEE
International Symposium on Information Theory,
Lausanne, Switzerland.
Dinoi, L., Sottile, F., Benedetto, S., 2005. Design of
Variable-rate Irregular LDPC Codes with Low Error
Floor. In Proceedings IEEE ICC, Seoul, South Korea.
Morelos-Zaragoza, R. 2002. The Art of Error Correcting
Coding. The John Wiley & Sons.
Prabhakar, A., Narayanan, K. 2002. Pseudorandom
construction of low-density parity-check codes using
linear congruential sequences. In IEEE Transactions
on Communications, vol. 50, no. 9, pp. 1389-1396.
Tian, T., Jones, C., Villasenor, J. D. and Wesel, R. D..
2004. Selective avoidance of cycles in irregular LDPC
code construction. In IEEE Transactions on
Communications., vol. 52, pp. 1242-1247.
Mao, Y. and Banihashemi, H. 2001. A heuristic search for
good low-density parity-check codes at short block
lengths. In Proceedings IEEE ICC, Helsinki, Finland.
Anderson, I. 1990. Combinatorial Designs: Construction
Methods. The Chischester, U.K.: Ellis Horwood.
Richardson, T. J., Shokrollahi, M. A. and Urbarke R. L.
2001. Design of capacity-approaching irregular low-
density parity check codes. In IEEE Transactions on
Information Theory, vol. 47, pp. 619-637.
Pérez, J.M. and Fernández, V. 2005. Hardware Aware
eIRA LDPC Code Generation. In Proceedings IEEE
ISWCS, Siena, Italy.
HIERARCHICAL AND PSEUDO-RANDOM EIRA CODES BASED ON BIBDS AND PRIMITIVE INTERLEAVERS
157
