SMOOTH BLOCKS-BASED BLIND WATERMARKING

ALGORITHM IN COMPRESSED DCT DOMAIN

Chun Qi, Haitao Zhou, Bin Long

Institute of Image Processing & Recognition, Xi’an Jiaotong University, 710049Xi’an, China

Keywords: Smooth blocks, Blind Watermarking, DCT, Weber’s Law, JPEG domain.

Abstract: A novel blind watermarking scheme based on smooth blocks in compressed DCT domain is proposed. The

smooth blocks are detected by a criterion which uses a relation between the quantized DC coefficients and

the variance of AC coefficients in the block and deduced from the Weber’s Law. In the approach, the

watermark is embedded by modifying the average value of some low-frequency DCT coefficients in

selected blocks, and recovered by the sign of the mean value of corresponding coefficients in detected

blocks and there is no need for original image. The experimental results demonstrate that almost no

perceptible distortion is found in the watermarked images, and the watermark is robust to some image

processing operations such as scaling, noise, filtering and JPEG compression.

1 INTRODUCTION

Many DCT-based watermarking schemes have been

proposed as a solution to the copyright protection of

multi-media recently. Suhail et al propose a digital

watermarking based on image segmentation (Suhail,

2003). Peter Wong et al hide data only in the texture

blocks (Wong, 2001). In block-based algorithms,

good care must be taken to avoid smooth (or non-

textured) blocks and edge blocks as modification of

these leads to annoying artifacts in the watermarked

image (Holliman, 1998).

Actually, we find that if we do some changes to

the low-frequency DCT coefficients of appropriate

smooth block, perceptible distortions would be

hardly found in the watermarked images. Moreover,

the watermark inserted in these smooth blocks is

robust to some image processing operations such as

filtering and JPEG compression. In this paper we

develop a new watermarking algorithm based on the

smooth blocks. A criterion is presented according to

the Weber’s Law to select these blocks. Different

tests are conducted to verify the performance of the

scheme under different types of attacks. The method

appears to be very robust to most image processing

operations. The paper is organized as follows.

Section 2 describes the embedding and extracting

techniques in details and Section 3 elaborates

various experimental results. Finally, Section 4 gives

the conclusions.

2 PROPOSED WATERMARKING

TECHNIQUE

In this section we describe our watermarking scheme

in detail, which is block-based and shares same

features with the JEPG standard for still image

compression. The quantized DC and the AC

coefficients denote the average luminance and the

different frequency band of a block which could

reflect its texture respectively (Jianmin, 2002). A

new approach to select the appropriate smooth

blocks is given as follows:

2.1 Classifying Smooth blocks

In this paper, we introduce a similar criterion (Lin,

2005

) based on the quantized DC coefficients and

variance of AC coefficients, which is deduced from

the well-known Weber’s Law (Gonzalez, 2002).

02.0≈

(1)

Where

denotes the object, and

denotes the

background. This equation is true only when the

range of

is in the middling intensity, which is

clearly shown in the Fig.1. The proposed classified

method bears a resemblance to the Weber’s Law:

Considering the average luminance and the texture

of a block as the background and the object mention-

347

Qi C. and Zhou H. (2006).

SMOOTH BLOCKS-BASED BLIND WATERMARKING ALGORITHM IN COMPRESSED DCT DOMAIN.

In Proceedings of the International Conference on Security and Cryptography, pages 347-350

DOI: 10.5220/0002098803470350

 SciTePress

Figure 1: Weber curve.

ed in the Weber’s Law, respectively. We can get a

similar equation from Eq. (1):

02.0≈

(2)

Where DC is the quantized DC coefficients of a

block, and

is the standard deviation of all the AC

coefficients in a block.

The Weber ratio mentioned in formula (2) is just a

critical value which can be used for classifying

blocks. Then we can get a general formula to select

the smooth blocks apart from other blocks.

DC×≤ 02.0

(3)

We can get an easy formula as follows after squaring

the both side

)02.0()var( DCAC ×≤

(4)

Where

)var( AC

and DC are the variance of the 63

quantized AC coefficients and the quantized DC

coefficient of a block, respectively.

In order to avoid selecting texture blocks we

should strictly choose the number of the smooth

blocks to improve this method. Here we adopt a

variable instead of the constant value 0.02 as the

following formula:

)()var( DCAC ×≤

(5)

Where

is an adaptive value according to the

feature of the image and

02.0

≤

However, some high intensity blocks are so

sensitive that they are not fit for watermark

embedding, which would cause severe visual

artefacts. Hence, a formula is given for excluding

these high intensity blocks as follows:

02.0

×≤ grayaverDC

(6)

Where

ave

denotes the average gray-scale of

the whole image.

As lower luminance blocks are less sensitive to

human eyes as can be seen from Fig.1, we should

reserve these lower intensity blocks which are

appropriate for embedding:

30=DC

(7)

Where the modified DC is just used for computation,

in some sense, and the original DC is recovered

when the selection of the block is completed.

2.2 Selecting Smooth Blocks

Smooth blocks are selected depending on formula

(5), (6) and (7). The number of smooth blocks we

choose is based on the size and characteristic of the

image. The detail steps of selecting appropriate

smooth blocks are described as follows:

1) First set

, and set n=0, where n is the

number of actually selected blocks.

2) The

is gradually increased by a step of

00025.0

, and

02.0

≤

. According to the

formula (5), (6) and (7). Record the value of

when

is increasing.

3) Thirdly, the loop is continued if

02.0

≤

and

≤

. Or, the loop is terminated. Then

selected blocks are obtained.

Appropriate blocks are selected according to the

three steps mentioned above. The number of selected

blocks is determined by the adaptive factor

and no

less than N=200, decided empirically, while the total

blocks of the standard image are 1024.

2.3 Watermark Embedding

Let

be an original gray-level image of size

NN ×

and the watermark w be a random bipolar binary

sequence that uniformly from{1,-1}, of which the

length is

64/)(

NNL

. During insertion,

performed

DCT. Then the quantized DCT

coefficients are sorted in zigzag order.

),( jiF

denotes

the j

quantized coefficients in zigzag order of the i

block. Three steps for embedding are as follows:

1) Choose the smooth blocks depending on the

Section 2.2. In this situation, we should promote

0005.0

, so that we could selected more

blocks than that of the extracting.

2) Assume the i

block is the smooth block that

we choose. Considered the robustness and invisi-

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

348

bility, the coefficients for modification are

)2,(iF

)3,(iF

)5,(iF

empirically. The average value of

the three coefficients:

3/)]5,()3,()2,([_ iFiFiFACaver +

(8)

If the watermark

1)(

=iw

, we should promote

the average value to the positive. The details are

as follows:

1_ ≥ACaver

, do not need to modify;

else if

1_0 <≤ ACaver

)_1(),(),(' ACaverjiFjiF −

(9)

Where

),(' jiF

is the modified coefficient, j=2, 3, 5.

else,

0_ <ACaver

)_(),(),(' ACaverfloorjiFjiF

−

(10)

Where floor(*) denotes the maximum integer that

is less than (*), and j=2, 3, 5.

If the watermark

1)( −

=iw

, we should demote

the average value to the negative. The details are

as follows:

1_ −≤ACaver

, do not need to modify;

else if

0_1 ≤<− ACaver

)_1(),(),(' ACaverjiFjiF −−+=

(11)

else

0_ >ACaver

)_(),(),(' ACaverceiljiFjiF

−

(12)

Where ceil(*) is the minimum integer that is

greater than (*), and j=2, 3, 5.

3) Repeat Step-2 until selected blocks are embedded

with watermarks. For the non-selected blocks, the

corresponding watermarking bit has no need to be

inserted. Then perform inverse DCT for those

blocks and finally obtain the watermarked image.

2.4 Watermark Extraction

The watermark extracting can be performed without

knowledge of the original image. Here are the steps

as follows:

1) Perform DCT compressed for each

block.

Select n blocks as mentioned in Section 2.2. Here

the

00025.0=Δ

is less than that of the inserting,

so some embedded blocks will be excluded as

the step halved of that of the embedding. We can

extract the information from these blocks.

2) For each selected block, the average of some

coefficients is computed as follows:

3/)]5,(')3,(')2,('['_ iFiFiFACAver +

(13)

Where

'_ ACAver

denotes the average value of

the three quantized AC coefficients, and

),(' jiF

denotes the j

quantized coefficients in

zigzag scanning order of the i

88×

block in the

watermarked image. The detected watermarking

bits are extracted according to sign of the average

value:

)'_()(' ACAversigniw

(14)

Where w’(i) indicate the extracted watermark,

and sign(*) is signed function.

For non-selected blocks such as those edge and

texture blocks, while the one is the

block of

the whole blocks, we set the corresponding

detected watermark information:

0)('

. (15)

Repeat this step for every block till the whole

detected watermarking sequence is obtained.

Then we can get the extracted watermark

sequence w’ from {1, 0, -1}, with the length of L

the same as the number of all the blocks. When

the detected watermark is from {1, -1}, it means

we get the valid watermark information; else if

is {0}, the corresponding watermark bit is useless.

3) To evaluate the similarity of the extracted and

the original, we measure the similarity by the

following correlation function :

∑∑

iwiwiwNC

)('/)(')(

(16)

Where L is the length of the watermark sequence,

which is same as the number of the whole blocks,

w(i) is the original watermark and w’(i) is the

extracted. NC is the normalized correlation,

which range from -1 to 1. If NC>T, it implies that

there is a watermark existing in the testing image,

where T is an experimental value.

3 EXPERIMENTAL RESULTS

Several common image processing operations and

geometric distortions were applied to these images

to evaluate whether the correlation output of detector

SMOOTH BLOCKS-BASED BLIND WATERMARKING ALGORITHM IN COMPRESSED DCT DOMAIN

349

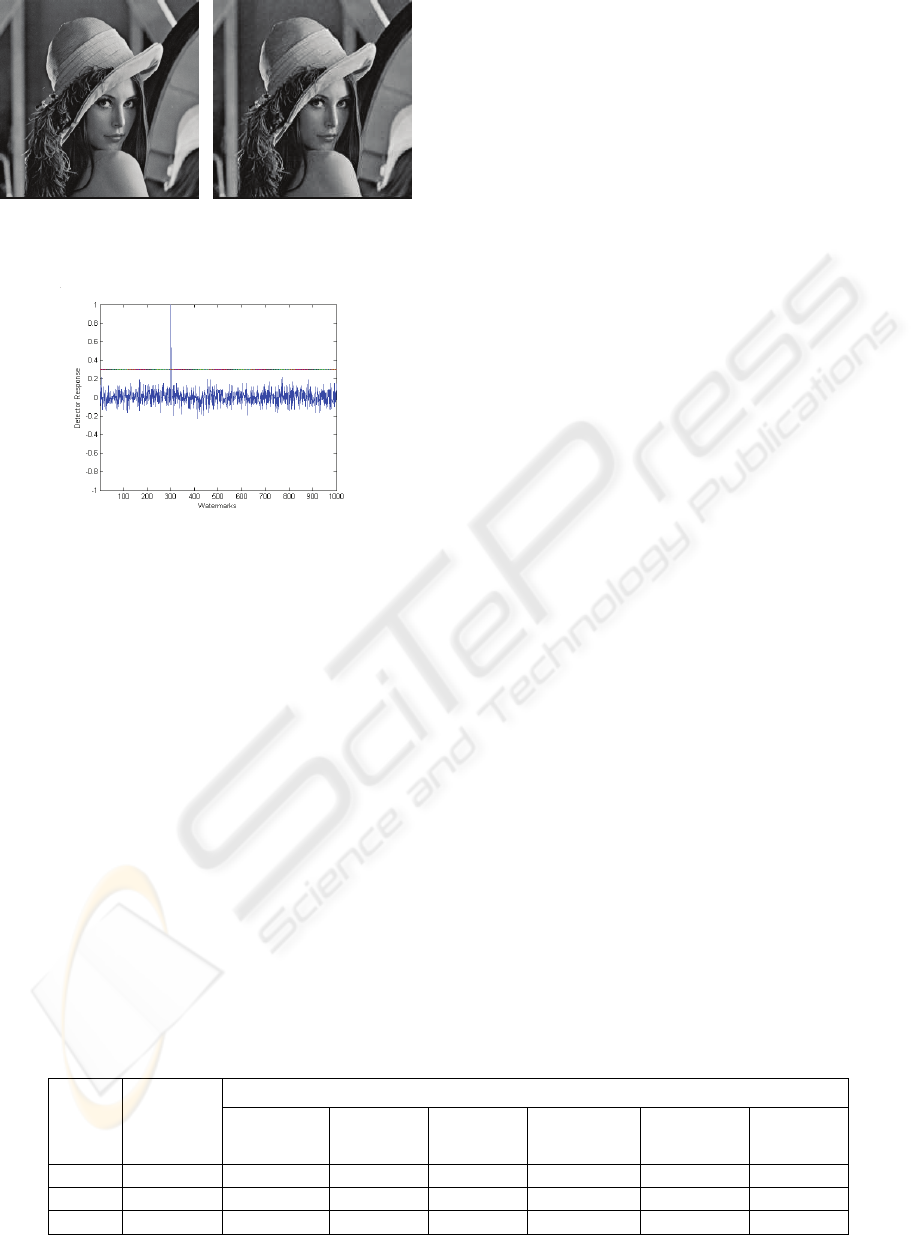
Figure 2: Original (right) and watermarked “Lena”(left) ,

PSNR=31.89db.

Figure 3: Bipolar detector output for Lena image, NC=1.00.

can reveal the existence of watermarking in the

images. Here we only show the result of “Lena” in

detail. Fig.2 shows both the original and the

watermarked images. Fig.3 illustrates uniqueness of

the watermark. The response of a given mark is

compared to

(

3.0=T

, an experimental value) to

decide whether the watermark is present or not.

Some attacks such as common image processing

operations and geometric distortions, are described

in Table 1. The check threshold is T=0.3. Due to the

space limitation of the paper, many other detailed

results and discussions are omitted. As shown in the

table, it can be indicated that the correlation output

is 1.0 for the three images when attack-free, and

PSNR is also appropriate, and both PSNR and NC

will drastically decline when the watermarked

images have some distortions. But NC is always no

less than the threshold (T=0.3), which means that the

watermark can be correctly detected even there are

some distortions. From this table, the robustness of

proposed scheme could be demonstrated.

4 CONCLUSION

Avoiding modifying smooth (or non-textured)

blocks and edge blocks during the watermarking

process is a traditional view. This paper proposes an

idea that watermarking can be embedded in smooth

blocks. Experimental results show that this technique

is robust to many standard image processing

operations and some geometric distortions. It is

clearly that robustness against median filtering and

Gaussian noise was achieved when the watermarked

images were seriously degraded. Some geometric

attacks can be resisted by the scheme. Moreover, the

proposed method doesn’t need to use the original

images during extracting watermark. In addition, the

proposed technique can also be extended to insertion

of invisible watermarks in digital video.

REFERENCES

M.A. Suhail, M.S., 2003. Digital watermarking-based

DCT and JPEG model. IEEE Trans. on Instrumenta-

tion and Measurements.

P.H. Wong, Au., 2001. A data hiding technique in JPEG

domain compressed domain. Proceeding of SPIE Conf.

of Security and Watermarking Multimedia Contents.

M. Holliman, N., 1998. Adaptive public watermarking of

DCT-based compressed images. Proc. Of SPIE-The

international society for optional engineering.

Jianmin J., G., 2002. The spatial relationship of DCT

coefficients between a block and its sub-blocks. IEEE

Trans. on Signal Processing.

F. Lin, L.YanJun and et al, 2005. A fast fractal image

coding method using the characteristics of human

vision system in DCT domain. Journal Of Computer-

Aided Design & Computer Graphics.

R.C. Gonzalez and R.E. Woods, 2002. The book, Digital

Image Processing.

Table 1: (PSNR/Bipolar NC) of Watermarked Images Under Various Attacks.

Attacks(our threshold T=0.3)

Test

images

Water-

maked

images

Median filter

(

77 ×

)

Histogram

equalization

Gaussian

Noise

Affine

Transform

(

261261

)

Randomly

move lines

(

230230

)

Scale down

to 0.3 of it’s

Original size

Lena 31.89/1.00 24.77/0.44 15.80/0.84 24.04/0.65 19.80/0.54 22.21/0.86 22.49/0.49

Camera 31.19/1.00 22.34/0.53 18.28/0.51 24.41/0.64 18.71/0.56 21.97/0.80 21.90/0.63

Bridge 25.24/1.00 19.23/0.30 18.06/0.58 22.96/0.76 16.65/0.47 19.15/0.58 19.21/0.33

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

350