
QUANTITATIVE ANALYSIS AND ENFORCEMENT OF THE
PRINCIPLE OF LEAST PRIVILEGE IN ROLE-BASED
ACCESS CONTROL
Chunren Lai
Department of Computer Science, University of Regina, Regina, SK, Canada S4S 0A2
Chang N. Zhang
Department of Computer Science, University of Regina, TRLabs, Regina, SK, Canada S4S 0A2
Keywords: Principle of least privilege, role based access control, system security, user-role assignment.
Abstract: Role-based access control (RBAC) models ease security administration and reduce overheads by
introducing roles between users and privileges. RBAC provides the possibility to enforce the principle of
least privileges that a user should be assigned just enough privileges to complete his/her job in order to
prevent the possible information leaking and other wrong doing. This paper defines several concepts to
quantitatively measure how well a user-role assignment meets the principle of least privilege and presents
algorithms to find the perfect user-role assignment (i.e., without bringing any extra privilege) and the
optimal user-role assignment (i.e., limiting any extra privilege to the minimum). The proposed approach for
the enforcement of the principle of least privilege is particularly useful for automatic generation of user-role
assignment in large-scale RBAC systems.
1 INTRODUCTION
Role-based access control (RBAC) ease security
administration and reduce overheads by introducing
roles between users and privileges (Giuri, 1997,
Sandu, 1996, Ferraiolo, 2001, Bertino, 2001). One of
the important features of RBAC models is that
RBAC can apply constraints, enforce the principle
of least privilege and other access control policies
(Osborn, 2000, Ann, 2000, Ferraiolo, 1993). The
principle of least privilege (Saltzer, 1975, Howard,
2003) requires that a user be assigned via roles just
enough privileges to complete his/her job and
receives minimum extra privileges. There are many
applications that need to conform the principle of
least privilege. In a task based RBAC system
(Bertino, 1999, Zhang, 2003), a system security
administrator often has to determine which set of
roles should be assigned to a new user so that the
new user can complete his/her tasks while
conforming the principle of least privilege. Another
application to conform the principle of least
privilege is to assign a set of roles to a user to
perform certain tasks in a role activation session.
Though the RBAC models enable the
enforcement of the principle of least privilege, little
research has been found in the literature about how
to efficiently and correctly apply the enforcement of
the principle of least privilege.
In this paper, we first introduce and define
several concepts to quantitatively measure how well
a user-role assignment meets the principle of least
privilege. With respect to the target privileges
required to complete a user’s job, we can quickly
determine whether or not there exists a perfect user-
role assignment (i.e., without bringing any extra
privilege except the ones required to complete the
job). We then propose two algorithms to find the
perfect user-role assignment if such an assignment
exists, and to find out an optimal user-role
assignment that has the smallest privilege leak in
case that a perfect user-role assignment does not
exist. The proposed analysis methods and algorithms
are particularly useful in large-scale RBAC systems
69
Lai C. and N. Zhang C. (2006).
QUANTITATIVE ANALYSIS AND ENFORCEMENT OF THE PRINCIPLE OF LEAST PRIVILEGE IN ROLE-BASED ACCESS CONTROL.
In Proceedings of the International Conference on Security and Cryptography, pages 69-74
DOI: 10.5220/0002100500690074
Copyright
c
SciTePress
in which it is difficult to enforce the principle of
least privilege by conventional methods.
The rest of this paper is organized as follows.
Next section briefly describes the role-base access
control models and the principle of least privilege.
Section 3 defines several concepts to quantitatively
measure the degree of how well a user-role
assignment meets the principle of least privilege. In
that section, we will also introduce the relationships
among those concepts. In section 4, we present
searching algorithms for the perfect and optimal
user-role assignments. A brief conclusion is
presented in section 5.
2 ROLE-BASED ACCESS
CONTROL AND THE
PRINCIPLE OF LEAST
PRIVILEGE
There are several RBAC models proposed in the
literature (Sandu, 1996, Ferraiolo, 2001, Bertino,
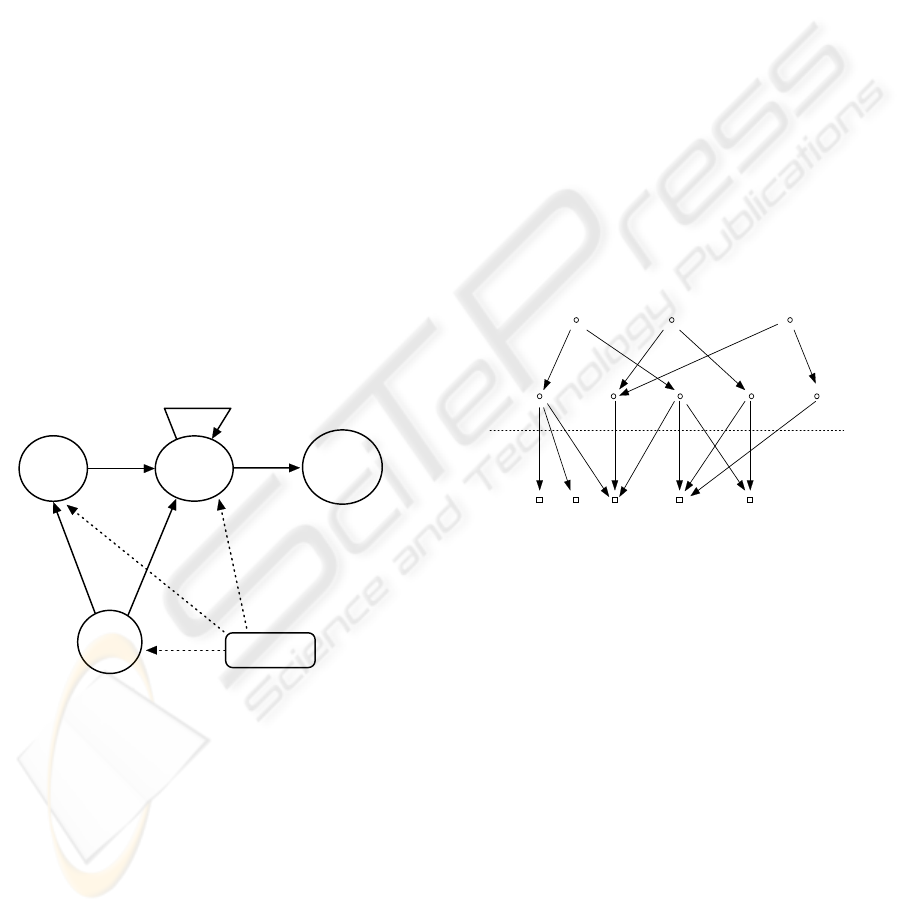
2001, Bertino, 1999, Zhang, 2003). Figure 1 shows
the logic diagram of the RBAC96 model proposed
by Sandu, 1996.
Users
Privileges
Roles
user-role
assignment
role-pr ivilege
assignment
role hierarchy
assignment
Session
role
activation
user
authorization
Constraints
Figure 1: A typical RBAC96 model.
There are three basic sets in the RBAC96 model:
U (a set of users), R (a set of roles that have
hierarchical structure), and P (a set of privileges).
Privileges are sometimes called permissions. There
are three assignments: user-role assignment: UA
⊆
U
× R; role hierarchy assignment: RH ⊆ R
×
R;
role-privilege assignment: RP
⊆ R × P.
The principle of least privilege was first
introduced by Saltzer, 1975. That is, every user and
every program of a system should operate using the
least set of privileges necessary to complete the job
(Saltzer, 1975). Essentially this principle limits the
potential damage from any accident or error, and
reduces the number of interactions among privileged
program to the minimum.
The advantages of the principle of least privilege
in the RBAC system are obvious. In one hand, it
reduces the security leak when assigning roles to
new users. In the other hand, by enforcing the
principle of least privilege, only necessary roles will
be activated in a session and thus it minimizes the
resource consumption of a system and reduces
errors.
3 QUANTITATIVE ANALYSIS
FOR THE ENFORCEMENT OF
THE PRINCIPLE OF LEAST
PRIVILEGE
An example of RBAC system is shown in figure 2
where the role-hierarchical structure and direct role-
privilege assignments are indicated.
Roles
Privileges
r1 r2 r8
r3
r4
r5
r6
r7
s1 s2 s3 s4 s5
Figure 2: An example of RBAC system.
Suppose that we need to assign a new user A
with a set of roles so that user A can complete a job
that requires privileges
3
s and
4
s . The question is
that which set of roles should be assigned to user A
in order to meet the principle of least privilege. To
solve the problem, we first define the representation
of the direct role-privilege assignments (DRPA). In
general, the DRPA can be represented by an m
×
n
direct role privilege matrix, where m is the number
of roles and n is the number of privileges. Each
element of DRPA is denoted by
[, ]drpa i j .
[, ] 1drpa i j
=
if role
i
r can directly access the
privilege
j
s
, otherwise,
[, ] 0drpa i j =
. In RBAC,
roles are organized as a hierarchical structure. For
example in figure 2, role
2
r inherits the privileges
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
70

from both roles
4
r
and
6
r , and therefore has
privileges of
3
s ,
4
s
and
5
s .
By taking the role hierarchical structure into
account, the DRPA can be extended into a role-
privilege relationship matrix (RP) that includes
direct and indirect role-privilege assignments.
Formally, the RP matrix can be defined as
follows.
Definition 1: Assume there are m roles and n
privileges in RBAC. A role privilege relationship
matrix
R
P is an mn× matrix where:
[, ] 1rp i j = if role
i
r can access the privilege
j
s ,
otherwise,
[, ] 0rp i j =
.
In many RBAC systems, we need to express the
relative significance of some privileges over others.
For example, in most database applications, people
often consider the privilege of “delete a record”
action is more significant than the one of “read a
record” action. The privilege weight matrix is to
represent different levels of importance of the
privileges. Formally, we have:
Definition 2: Assume there are n privileges in
RBAC. A privilege weight array
PW is a
1 n× matrix where its element []
p
wj is defined as
the relative significance factor of the privilege
j
s
among the n privileges, where
0[]1.0pw j<≤
for
1 jn≤≤.
An example of
PW for the privileges in figure 2
can be:
[
1.0PW = 0.5 1.0 1.0
]
0.5 .
Definition 3: Assume there are n privileges in
RBAC. A target privilege array
TP is a
1 n× matrix where its element []tp j is defined by:
[] 1tp j = if
j
s is the target privilege, otherwise,
[] 0tp j = for 1
j
n≤≤.
The target privileges are the privileges that are
required by a user to complete his/her job. We
assume that the target privileges are
3
s and
4
s in
our example, so the target privilege matrix is:
[
0TP = 0 1 1
]
0 .
Let
R
be a set of l roles, i.e,
{ | 1,..., }
j
k
R
rj l== that is assigned to a user.
Definition 4: The privilege preservation degree
R
β
is defined as follows:
R
β
= (sum of weights of target privileges that
R
can access) / (sum of weights of privileges that
R
can access).
For example in figure 2, we have:
3
{}r
β
= pw[3]
/ (pw[1]+ pw[2]+pw[3]) = 1.0/2.5 = 0.4. Similarly,
1
{}r
β
= 0.5.
R
β
represents the degree in which how the role
set
R
preserves the target privileges with respect to
all the privileges that the role set
R
can access. If
R
β
=1, it means that the role set
R
can and only
can access target privileges. If
R
β
<1, it means that
the role set
R
can access at least one non-target
privilege. A privilege leaking occurs when
R
β
<1.
Definition 5: Fulfillment degree
R
γ
is defined as
follows:
R
γ
= (sum of weights of target privileges
that
R
can access) / (sum of weights of all target
privileges).
For the same example, we have,
3
{}r
γ
= (pw[3]) /
(pw[3]+pw[4]) = 1.0/2.0 = 0.5. Similarly,
1
{}r
γ
= 1.0
and
47
{,}rr
γ
= 1.0. If
R
γ
=1, it means that the role set
R
can access all the target privileges.
Definition 6: The overall satisfaction degree
R
ϕ
is defined as follows:
R
ϕ
=
R
β
•
R
γ
If
R
ϕ
=1, it means that the role set
R
fully
satisfies the principle of least privilege. If
R
ϕ
<1, it
means that either
R
is not able to access all target
privileges or
R
can access at least one non-target
privilege.
Definition 7: A role set
R
is perfect if
R
ϕ
=1.0
According to the above definitions, we have:
Theorem 1: A single role
k
r is perfect if
[,] []rp k j tp j
=
for all
1 jn
≤
≤
.
Proof: If
[,] []rp k j tp j
=
for all 1
j
n≤≤, it
means that role
k
r can and only can access target
privileges, so we have
{}
k
r
β
1.0=
and
{}
k
r
γ
1.0
=
according to definition 4 and definition 5, and thus
{}
k
r
ϕ
1.0
=
. According to Definition 7, we can
conclude that the single role
k
r is perfect.
QUANTITATIVE ANALYSIS AND ENFORCEMENT OF THE PRINCIPLE OF LEAST PRIVILEGE IN ROLE-BASED
71

In the example of figure 2, the single role
8
r is
perfect.
Definition 8: Target privilege accessibility array
TPA is an
1m× matrix and defined by:
[]tpa i =
1
([,] [])
n
j
rp i j tp j
=
∨∧, for
1 im
≤
≤
,
where
∧ is logic AND operation, and ∨ is logic
OR operation.
TPA defines the property of whether a role can
access any target privilege. If
[]tpa k =1, it means
that the role
k
r can access at least one target
privilege. If
[]tpa k =0, then the role
k
r cannot
access any target privilege.
Definition 9: Non-target privilege accessibility
array NTPA is an
1m×
matrix and defined as:
[]ntpa i =
1
([,](1 []))
n
j
rp i j tp j
=
∨∧−
NTPA defines whether a role can access any
non-target privilege. If
[]ntpa k =1, it means that
the role
k
r can access at least one non-target
privilege. If
[]ntpa k
=0, then the role
k
r cannot
access any non-target privilege.
Theorem 2:
Let
1
([](1 []))
m
i
Stpai ntpai
=
=∨ ∧ − . If S =0, then
there does not exist a role set
R
that is perfect.
Proof: If
S =0, then all
[] (1 [])tpa i ntpa i∧− =0 for1 im≤≤ , so we
have
[]tpa i
=0 or
[]ntpa i
=1 for any role
i
r . It
means that any role either cannot access any target
privilege or can access at least one non-target
privilege. That is, any role set
R
formed from any
combinations of roles
i
r (1 im≤≤ ) is not perfect.
It concludes that there is not perfect role set.
Theorem 2 implies that S=1 is the necessary
condition for a role set to be perfect.
A perfect role set has an important property that
is described by the following theorem. This property
provides the guidelines to find the perfect role set
efficiently.
Theorem 3: If a role set
R
is perfect, then every
role
k
r in
R
satisfies: []ntpa k =0.
Proof: If the role set
R
is perfect, then
R
β
=1.0
according to Theorem 1. From
R
β
=1.0, we know
that none of the roles in
R
β
can access any non-
target privilege. According to the Definition 9, we
have
[]ntpa k =0 for every role
k
r in
R
β
.
Definition 10: A role
w
r (
1 wm≤≤
) is a must-
in role of the target privilege
v
s (i.e., [] 1tp v
=
,
1 vn
≤
≤
) if
w
r is the only one role that can
access the target privilege
v
s . A must-in role is
marked as
ˆ
v
r .
The must-in roles are the roles that must be
included in the user-role assignment. The existence
of must-in roles can significantly reduce the
searching time for the user-role assignment to
conform the principle of least privilege. The
following algorithm searches the must-in roles for
each target privilege. If the must-in role does not
exist for a target privilege, it is set to be
φ
.
Algorithm 1: find must-in roles for each target
privilege.
Input:
R
P , TP
Output: must-in roles for each target privilege
Step 1: For j=1 to n, do
Step 1.1: If
[] 1tp j
≠
, then goto step 1
Step 1.2:
ˆ
j
r
φ
=
Step 1.3. k =
1
[, ]
m
i
rp i j
=
∑
; if 1k ≠ , then goto
step 1
Step 1.4: For i=1 to m, do
Step 1.4.1: if
[, ] 1rp i j = , then
ˆ
j
i
rr
=
Step 2: Halt;
4 ALGORITHMS TO FIND USER-
ROLE ASSIGNMENT MEETING
THE PRINCIPLE OF LEAST
PRIVILEGE
4.1 Algorithm to Find a Perfect
User-role Assignment
Algorithm 2: find perfect role set
R
.
Input:
R
P , TP , PW
Output: A perfect role set
R
or reporting “no
solution”.
Step 1: Calculate
TPA , NTPA , S
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
72

Step 2: If
S
=0, then report “No perfect role set
solution”, and goto step 7.
Step 3: For i=1 to m, do
Step 3.1: If
[, ] [ ]rp i j tp j
=
for all 1
j
n
≤
≤ ,
then output
{}
i
R
r= , and goto step 7.
Step 4: Assume q is the number of roles that
satisfy:
[] 1
z
tpa i = and [] 0
z
ntpa i = , where
1 zq≤≤.
Step 5: For b=2 to q, do
Step 5.1: Pick up b roles from the q roles (i.e.,
1
i
r ,
2
i
r , …,
q
i
r ) to form the role set
b
R
.
5.1.1: If
b
R
ϕ
=1, then output the role set
R
=
b
R
,
and goto Step 7.
Step 5.2: Repeat step 5.1 until no more
combinations of b roles.
Step 6: Reporting “No perfect role set solution”
Step 7: Halt;
The strategy of Algorithm 2 to find a perfect role
set
R
is: (1) If S=0, then there is no perfect role set
based on Theorem 2, and the algorithm exits
immediately; (2) If S=1, then step 3.1 checks
whether any single role is perfect based on the
Theorem 1. If such a single role is found, output the
result and exit. (3) If no single role is a perfect role
set, then consider any combinations of appropriate
roles according to Definition 7. This is done in step
5.
For the example in figure 2, the single role
8
r is
found as a perfect role set.
4.2 Algorithm to Find Optimal Role
Set that Meets the Principle of
Least Privilege
In the case that perfect role-assignment does not
exist, we first search all possible role sets that have a
target privilege fulfillment
R
γ
=1.0, and then sort
them by the value of overall satisfaction degree
R
ϕ
.
Based on our definition of
R
ϕ
, the bigger the value
of
R
ϕ
is, the better the role set
R
meets the
principle of least privilege.
The role set
R
with the maximum
ϕ
value is
called the optimal role set. We assume that the role
constraints C should be taken into consideration
when searching the role set.
Algorithm 3: find the role set that conforms the
principle of least privilege
Input:
R
P , TP ,
PW
, DRPA, C (role
constraints)
Output: Either an optimal role set
R
that can
access all target privileges, satisfies the constraints C
and conforms the principle of least privilege, or
reporting “no solution”.
Step 1: k=0; find must-in roles for each target
privilege based on algorithm 1;
Step 2: For each j that satisfies
[]tp j =1, do
Step 2.1: k=k+1; set role set
k
R
I
=
φ
;
[]nk
=0;
Step 2.2: If
ˆ
j
r
φ
≠
, then
k
R
I
=
ˆ
j
r , []nk =1,
and continue step 2;
Step 2.3: For i=1 to m do
Step 2.3.1 If
[, ]drpa i j =1 and role
i
r satisfies
the constraints C, then add
i
r to
k
R
I
, and set
[]nk
=
[]nk +1;
Step 2.4: If
[]nk =0, then reporting “No
solution” and goto step 7.
Step 3: Pick one role from each role set
i
R
I
(where
1 ik
≤
≤ ), and combine those roles to form
a new role set
j
TR
(where
1
1[]
k
i
j
ni
=
≤≤
∏
).
Step 4: Set
max
ϕ
=0 and Z=0;
Step5: For j=1 to
1
[]
k
i
ni
=
∏
, do
Step 5.1: If role set
j
TR
does not satisfy the role
constraints C, then goto step 5.
Step 5.2: Calculate
j
TR
ϕ
;
Step 5.3: If
j
TR
ϕ
>
max
ϕ
, then
max
ϕ
=
j
TR
ϕ
and Z=j;
Step 6: If Z>0 then Output the role set
Z
TR
(i.e.,
Z
TR
is the role set that can access all target
privileges, satisfies the constraints C and conforms
the principle of least privilege), otherwise reporting
“No solution”.
Step 7: Halt.
In the role hierarchical structure, high-level roles
inherit the privileges from all their low-level roles,
and all the roles that we are searching for should be
in the lowest level, otherwise they may bring extra
non-target privileges and thus can violate the
principle of least privilege. That is, for any target
QUANTITATIVE ANALYSIS AND ENFORCEMENT OF THE PRINCIPLE OF LEAST PRIVILEGE IN ROLE-BASED
73

privilege
j
s , the target role
i
r should satisfy
[, ]drpa i j =1. Step 2 builds a temporary role set
i
R
I
from each target privilege (where1 ik≤≤ , k is
the number of the target privileges), and set the
temporary role set as must-in role if the must-in role
exists for the target privilege. Step 3 generates all
possible role sets
j
TR
by picking up one role from
each
i
R
I
. Step 5 sorts the overall satisfaction degree
j
TR
ϕ
. The combined role set
Z
TR
with the biggest
value of
max
ϕ
is the role set that we are searching
for. Because of the role constraints C, it is possible
that there does not exist such a role set that can
access all target privileges and satisfy the role
constraints C.
In a large-scale RBAC system, it requires quite
amount of computation in the step 3 and step 5 of
the Algorithm 3, and it is difficult or impossible to
enforce the principle of least privilege based on
intuitive observations or conventional approaches
for user-role assignments. The Algorithm 3 can thus
be used for the automatic generation of user-role
assignment that conforms the principle of least
privilege.
5 CONCLUSION
The principle of least privilege is important to many
RBAC applications. In this paper, we introduced and
defined the concepts to quantitatively measure the
enforcement of the principle of least privileges.
Two algorithms to find the perfect and optimal user-
role assignments that meet the principle of least
privilege are presented. The proposed approach for
the enforcement of least principle is particularly
useful for automatic generation of user-role
assignment in large-scale RBAC systems in which it
is difficult to enforce the principle of least privilege
based on intuitive observations or conventional
approaches for user-role assignments.
REFERENCES
Ahn, G., and Sandhu, R., 2000. Role-based authorization
constraints specification. ACM Transactions on
Information and System Security, Vol. 3 No. 4,
November 2000, pp 207-226.
Bertino, E., Bonatti, P. A., and Ferrari,E., 2001. TRBAC:
A temporal role-based access control model. ACM
Transactions on Information & System Security, Vol.
4, No. 3, Aug.2001, pp 191-233.
Bertino, E., Ferrari, E., and Atluri, V., 1999. The
specification and enforcement of authorization
constraints in workflow management systems. ACM
Transactions on Information and System Security,
Vol. 2, No. 1, 1999, pp 65-104.
Ferraiolo, D. F., Gilbert, D. M., and Lynch, N., 1993. An
examination of federal and commercial access control
policy needs. In Proceedings of NISTNCSC National
Computer Security Conference, Baltimore, MD,
September 1993, pp 107-116.
Ferraiolo, D. F., Sandhu, R., Gavrila, S., Kuhn, D. R.,
Chandramouli, R., 2001. Proposed NIST standard for
role-based access Control. ACM Transactions on
Information and System Security, Vol. 4, No. 3,
August 2001, pp 224-274.
Giuri, L., 1997. Role-based access control: A natural
approach. In Proceedings of the 1st ACM Workshop
on Role-Based Access Control, ACM, 1997, Pages II,
pp 33-37.
Howard, M., and LeBlanc, D., 2003. Writing secure code.
Microsoft Press, 2003.
Osborn, S., Sandhu, R., and Munawer, Q., 2000.
Configuring role-based access control to enforce
mandatory and discretionary access control policies.
ACM Transactions on Information and System
Security, Vol. 3, No. 2, May 2000, pp 85-106.
Sandhu, R., Coyne, E. J., Feinstein, H. L., Youman, C.
E., 1996. Role-based access control models. IEEE
Computer, Vol. 29, No. 2, IEEE Press, February 1996,
pp 38-47.
Saltzer, J. H., and Schroeder, M.D., 1975. The protection
of information in computer systems. Proceedings of
the IEEE, Vol. 63, No. 9, September 1975, pp 1278-
1308.
Zhang, C. N. and Yang, C., 2003. Integrating object-
oriented role-based access control model with
mandatory access control principles. The Journal of
Computer Information Systems, Vol. 43, No. 3, 2003,
pp 40-49.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
74
