FORWARD-SECURE AUTHENTICATED-ENCRYPTION

IN MULTI-RECEIVER SETTING

Kan Yasuda, Kazumaro Aoki, Eiichiro Fujisaki and Atsushi Fujioka

NTT Information Sharing Platform Laboratories, Nippon Telegraph and Telephone Corporation

1-1 Hikarinooka Yokosuka-shi, Kanagawa-ken 239-0847 Japan

Keywords:

Authenticated encryption, strong integrity, multi-receiver setting, forward security, packet-loss detection, DoS

attack, message authentication code, pseudo-random bit generator, target-collision-resistant hash-function.

Abstract:

In this paper we study a generic construction of forward-secure authenticated-encryption in unidirectional,

multi-receiver setting. By “multi-receiver setting” we mean the situation in which a single center transmits

large data to a dynamically changing group of receivers. In such scenario a direct application of bidirectional,

unicast methods would lead to multiple problems. In particular, we focus on the problem of vulnerability

against a type of denial-of-service (DoS) attack. We show that this problem can be effectively resolved by a

mechanism we call “MAC-then-MAC” structure. As the name suggests, this structure uses two independent

MACs, but we illustrate how it can be realized without losing efﬁciency in transmission rate, storage size

and computational overhead. Despite the fact that one of the MACs uses a constant key, our construction

guarantees integrity in the sense of forward security. We provide a concrete security model showing that

our construction achieves conﬁdentiality and strong integrity (replay avoidance, in-order packet delivery, etc.)

both in the sense of forward security.

1 INTRODUCTION

The area of authenticated encryption deals with

symmetric-key techniques to provide both conﬁden-

tiality and integrity. It can be realized by a generic

composition of a symmetric-key cipher and a mes-

sage authentication code (MAC) (Bellare and Nam-

prempre, 2000), which works well in unicast setting.

On the other hand, in multi-receiver setting, where

a single center transmits large data to a dynamically

changing group of receivers, multiple problems arise

in constructing authenticated encryption (Note that

in such scenario the communication becomes unidi-

rectional from the service provider to each user, af-

ter secret keys are once distributed to users.) One

problem is inefﬁciency; the direct application of uni-

cast authenticated-encryption would cause overhead

in transmission rate and in center’s computation. An-

other problem is that the unidirectional aspect de-

mands the mechanism of packet-loss detection in pas-

sive mode, in addition to other integrity requirements

such as replay avoidance and in-order packet delivery.

In this paper we focus on another problem in realiz-

ing authenticated encryption in multi-receiver setting:

forward security. Note that in multi-receiver setting,

secret keys, as many as the number of users, are in-

volved. These keys are long-lived, so they are always

under the risk of being compromised.

In general, the forward security of authenticated

encryption can be realized by combining a pseudo-

random number/bit generator (PRNG) and updating

the secret keys periodically (Bellare and Yee, 2003).

In multi-receiver setting, however, its unidirectional

aspect makes it difﬁcult to update the keys in syn-

chrony between the center and each user. The uni-

directional transmission also leaves the PRNG+MAC

method (which assures the integrity well in the sense

of forward security in bidirectional communication)

vulnerable against a type of denial-of-service (DoS)

attack.

The contribution of this paper is to provide a con-

crete, provably-secure construction of authenticated

encryption that resist against this DoS attack. The

DoS attack is overcome by a generic construction we

call “MAC-then-MAC” structure. This structure, as

its name suggests, uses two independent MACs and

hence would introduce inefﬁciency in transmission

rate, storage (key) size and computational overhead.

Yet, it turns out that the MAC-then-MAC structure

possesses a property with which we can suppress the

141

Yasuda K., Aoki K., Fujisaki E. and Fujioka A. (2006).

FORWARD-SECURE AUTHENTICATED-ENCRYPTION IN MULTI-RECEIVER SETTING.

In Proceedings of the International Conference on Security and Cryptography, pages 141-148

DOI: 10.5220/0002101501410148

 SciTePress

increase in bandwidth and storage size. The computa-

tional inefﬁciency can be resolved by an introduction

of keyed hash-function. We also show that our con-

struction attains conﬁdentiality and strong integrity in

the sense of forward security, even though one of the

MACs uses a constant key.

ORGANIZATION OF THIS PAPER. In Section 2 we

provide the background and previous works for the

topics discussed in this paper. In Section 3 we de-

scribe a naive construction based on previous tech-

niques, which assures conﬁdentiality and strong in-

tegrity in the sense of forward security but is vulner-

able against the DoS attack. Then we provide an im-

proved construction in Section 4 with the MAC-then-

MAC structure, which resists against the DoS attack

without losing efﬁciency. Precise deﬁnitions of our

algorithms are given in Section 5. Sections 6 and 7 are

devoted for the security analysis of our scheme. Our

security proofs are conducted in the concrete secu-

rity model (Bellare et al., 1997). This model is more

suited to symmetric-key setting than the asymptotic,

polynomial-reduction security model, for in practice

a symmetric-key primitive is usually equipped with

a ﬁxed security parameter. In Section 8 we discuss

practical instantiations of our construction. Section 9

concludes this paper.

2 PRELIMINARIES

RELATED WORKS. (Park et al., 2002) studies efﬁ-

cient approaches for authentication in multicast, com-

bining a digital signature with other techniques. In

particular, their construction is robust against packet

loss and suited for authenticating real-time streamed

data (Golle and Modadugu, 2001). There are also

works that deal with efﬁcient methods for key man-

agement (Wong et al., 2000). Among them, there

is an area called “broadcast encryption” (Naor et al.,

2001) which focuses on the conﬁdentiality aspect

and gives efﬁcient methods for key distribution and

mechanisms of traitor tracing. Practical services

that ﬁt into this setting include the distribution of

the recent work (Ray et al., 2005) which gives an

RSA-based multicast scheme with an added feature of

anonymity. Most of the above works either depend on

asymmetric-key techniques or involve rather sophis-

ticated ways to manage secret keys, and converting

these mechanisms into the form of forward security

does not seem trivial. So we do not go into the details

here.

BASIC APPROACH (TWO-STAGE ENCRYPTION). In

this paper we adopt a straight-forward approach for

key distribution, as follows: We assume that the cen-

ter distributes an independently random secret-key k

to each user u prior to transmission of data. Then

the center uses a fresh, random session-key K for

each message m . m is encrypted via a symmetric-

key cipher E : {0, 1}

× {0, 1}

∗

→ {0, 1}

∗

as c ←

(m), and K is encrypted via another symmetric-

key cipher

E as

h ←

(K) (here the vector no-

tations mean h

←

(K) for each u), where

k = (k

)

u∈P

is the vector of long-lived secret keys

for the set P of permitted users. Then the encrypted

datum (c,

h) consisting of ciphertext and header is de-

livered to the permitted receivers. This two-stage en-

cryption improves the efﬁciency (as compared to en-

crypting the large message m with each k

) and at

least assures conﬁdentiality. This method is suited for

a situation with a relatively small number of users and

provides a practically efﬁcient solution as long as the

size of header

h is kept minimal.

PRACTICAL SERVICES. In multi-receiver scenario

considered in this paper, a user may be revoked or

re-joined upon the decision of the sender; the center

may update the list of recipients dynamically during a

sequence of transmissions. Practical services that ﬁt

into this setting include the distribution of mail mag-

azine and the multicast of pay contents: A user may

wish to be unsubscribed from the mail magazine any

time during the service, or the service provider may

wish to default temporarily the transmission of con-

tents to those who have failed to pay.

AUTHENTICATED ENCRYPTION (“ENCRYPT-THEN-

MAC”). A mechanism of authenticated encryption

can be realized either by a dedicated scheme or by

a generic composition of a symmetric cipher and a

MAC (Bellare and Namprempre, 2000). Applica-

bility of dedicated schemes to multi-receiver setting

heavily depends on the structure of each scheme,

while the generic composition paradigm gives us scal-

ability. So we adopt the well-known “Encrypt-then-

MAC” composition (Bellare and Namprempre, 2000)

as our starting point.

STRONG INTEGRITY AND COUNTER. The traditional

notion of integrity deals with protecting data con-

tents from being modiﬁed. An appropriate usage of

a MAC would be adequate for this purpose. How-

ever, this does not sufﬁce to guarantee the strong in-

tegrity required in practice, such as replay avoidance

and in-order packet delivery (Kohno et al., 2003). The

strong integrity is a highly desirable property in multi-

receiver services.

The strong integrity of a sequence of ciphertexts

can be assured in several ways. Among them is to as-

sign a counter (like the “sequence number” used in

SSL) to each ciphertext (Note that the counter can

be sent in the clear. Also note that the size of the

counter, which correspondingly establishes its range,

must be large enough to meet the security objectives.

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

142

Preferably, it should be as large as the security param-

eter.) This counter method works effectively even in

the unidirectional setting, so we adopt this method as

our starting point.

PACKET-LOSS DETECTION. In this paper we require

each user u’s ability for packet-loss detection in a pas-

sive manner. This mechanism is quite important in

multi-receiver scenario, as explained in the following:

Suppose the center transmits ciphertexts C

, . . . , C

in this order. Then some intermediate C

may not be

delivered correctly to a permitted user u, for multi-

ple reasons. One possible reason is that noises on the

network may cause a damage to C

, resulting u to re-

ject the received ciphertext. Another possible situa-

tion is the case of mail magazine; the receiving server

(mail transfer agent, MTA) for u may happen to be out

of service on transferring C

. Upon failure, an error

code may be sent back (automatically) by the MTA

to the service provider, but the service provider may

not care for re-sending the old data. In case of stateful

encryption, it may be even impossible for the service

provider to re-send the exactly same ciphertext C

. In

these cases it is highly desirable that the user u be

able to detect the packet loss for C

, upon decrypting

the following (intact) ciphertext C

i+1

. We also note

that it is too optimistic to hope that C

, . . . , C

reach

every user in the correct order, when we think of the

evolving complexities of routing architecture in the

Internet.

FORWARD SECURITY VIA PRNG. The forward se-

curity of authenticated encryption can be realized by

key-update via a stateful PRNG (Bellare and Yee,

2003). If the combined PRNG is forward secure, then

the resulting authenticated-encryption scheme attains

forward security of both conﬁdentiality and (tradi-

tional) integrity (Bellare and Yee, 2003).

A stateful PRNG G : {0, 1}

→ {0, 1}

+κ

is a

deterministic algorithm that takes as its input the cur-

rent state s

and outputs (s

i+1

, k

i+1

) ← G(s

), where

i+1

is the next state and k

i+1

the updated key. The

secret key k

is used by the underlying symmetric-key

cipher and MAC. Note that the current stage number

i must be attached to the ciphertext/tag and sent in

the clear, so that the receiver can update his key in

synchrony and decrypt/verify with the key of correct

stage.

LIFE CYCLE OF SECRET KEYS. The length of a ses-

sion for using the same secret key k

must be agreed

between the sender and the receiver, so that the com-

municating party can update the secret key in syn-

chrony. The frequency of key update reﬂects the pol-

icy of the service and may be decided in terms of ei-

ther the time-span or the number of encrypted mes-

sages. The former is not suited in multi-receiver set-

ting, because a user may be excluded from the service

for a long period of time. The latter is more suited,

but note that the center needs to maintain the record

of the number of messages encrypted with the current

key k

for each user u.

VULNERABILITY AGAINST DOS ATTACK. The

PRNG+MAC method experiences the following DoS

attack in unidirectional setting: The adversary sends

to u bogus ciphertexts C

′

, C

′

, . . . with stage numbers

′(u)

, i

′(u)

, . . . ≫ i

(u)

, where i

(u)

is the current stage

number of u. Then u needs to investigate each C

′

its contents are forged or left intact, so that in the latter

case u can store C

′

and wait for missing ciphertexts

between i

(u)

and i

′(u)

to arrive.

If u performs the on-the-ﬂy integrity-check for

each C

′

, then each integrity-check requires (i

′(u)

−

(u)

)-many invocations of G, expending u’s compu-

tational resources. If u simply stores every C

′

into

memory without integrity-check, then it would ﬂood

u’s memory. If u saves intermediate state/key in-

formation into memory upon decrypting the ﬁrst C

′

then it would still need huge memory and undesirably

increase the risk of state/key compromise.

3 NAIVE COMPOSITION:

TWO-STAGE ENCRYPTION +

“ENCRYPT-THEN-MAC” +

COUNTER + PRNG

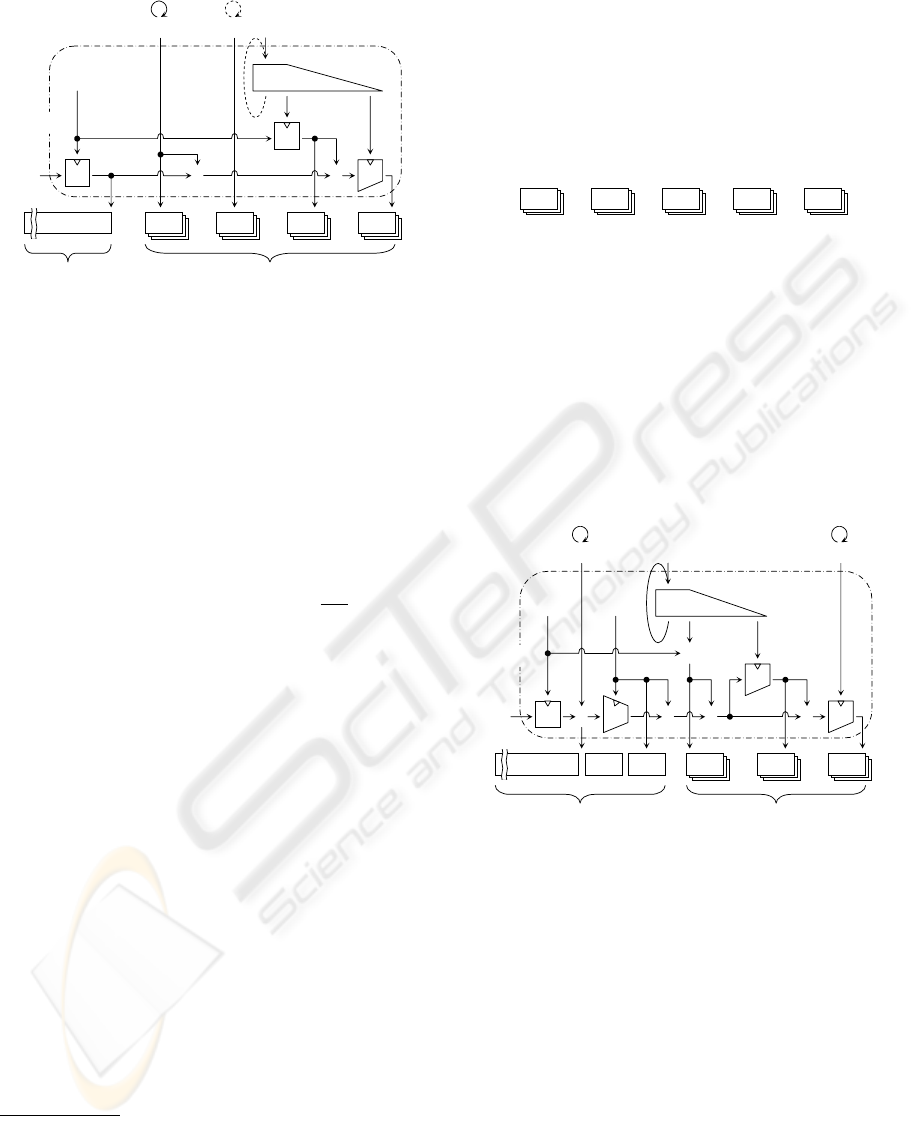
Figure 1 illustrates a naive construction of encryption

algorithm, which is vulnerable against the DoS attack

but provides a prototype for our construction. It is

based on the well-known “Encrypt-then-MAC” com-

position (Bellare and Namprempre, 2000) applied to

the two-stage encryption via symmetric-key ciphers

E and

E with a MAC

T : {0, 1}

× {0, 1}

∗

→

{0, 1}

. Each user u’s counter ctr

(u)

is attached to

the ciphertext in order to attain the strong integrity.

The long-lived secret keys k

(u)

for

E and k

(u)

for

T are updated via PRNG G (Bellare and Yee, 2003)

for the purpose of forward security. G operates as

(u)

, k

(u)

, k

(u)

) ← G(s

(u)

) and is associated with

the stage number i

(u)

. In Figure 1 the variables with

a superscript “(u)” are unique to each receiver u,

and those without superscripts are common to all re-

ceivers.

The encryption algorithm E takes as its input the

message m ∈ {0, 1}

∗

and outputs the ciphertext C =

(c,

h) with

h = (h

(u)

)

u∈P

. u’s header h

(u)

consists

of ctr

(u)

tag

(u)

, and P denotes the set of

permitted users.

In the following we list some (negative) aspects of

this construction:

FORWARD-SECURE AUTHENTICATED-ENCRYPTION IN MULTI-RECEIVER SETTING

143

(u)



(u)

ctr

(u)

ctr

(u)



(u)

tag

(u)

–

c h

(u)

¯ ¯

Figure 1: Naive construction of encryption algorithm.

STRONG REQUIREMENT FOR

E. Under chosen-

plaintext attacks

against this scheme, the symmetric-

key cipher

E needs to be secure against known-

plaintext attacks; the long-lived secret key k

(u)

is used

for encrypting multiple session-keys K, even though

the adversary cannot choose the input K. Note that,

on the other hand, the symmetric-key cipher E only

needs to be one-time secure, because the session-key

K is used for encrypting only a single message.

OVERHEAD IN COMPUTING TAGS. In Figure 1 the

center needs to compute as many tags tag

(u)

as the

number of receivers, with the large ciphertext c as

a part of the input. Inputting c into the MAC

with each user’s secret key k

(u)

is necessary, be-

cause MACing instead with a common (fresh, ran-

dom) session-key would lead to a trivial attack by a

revoked user.

INDIVIDUAL COUNTER ctr

(u)

. In Figure 1 the center

needs to assign an individual counter ctr

(u)

to each

user u. The assignment of individual counter is nec-

essary for the packet-loss detection and for the man-

agement of key-update frequency.

Note that the usage of a counter common to all

users would no longer guarantee the users’ ability for

packet-loss detection in a passive manner; the receiver

cannot distinguish if the missing ciphertexts are lost

due to (adversarial) network damage or if they are

skipped due to the fact that the receiver in question

has been excluded during the period. It would also

disable the management of life cycles of secret keys.

INDIVIDUAL STAGE-NUMBER i

(u)

. The individual

stage number i

(u)

also increases the size of header

It sufﬁces to consider only the chosen-plaintext attacks

here, because we shall consider the integrity requirements

separately. The security against chosen-plaintext/ciphertext

attacks would then follow immediately, provided that those

returned by the encryption oracle are never queried to the

decryption oracle.

(u)

and the center’s storage. Note that if one uses

a common stage number, then a long-revoked user,

upon re-joining, must perform the computation of G

many times in order to obtain the current secret-key.

STORAGE SIZE. Figure 2 shows the storage at the

center. It can be minimized down to (ctr

(u)

, s

(u)

)

, if

(u)

is deduced from ctr

(u)

and k

(u)

, k

(u)

by s

(u)

ctr

(u)

Figure 2: Storage with the naive construction.

4 PROPOSED SOLUTION

In this section we modify the construction described

in Section 3, introducing the MAC-then-MAC struc-

ture. Our improved encryption algorithm E is de-

scribed in Figure 3.

(u)

tag

(u)

⊕

c ˆ



ctr



(u)

tag

(u)

ctr

(u)

tag

(u)

–

c ˆ

c h

(u)

Figure 3: Improved construction of encryption algorithm.

In the following we list some of the key points in

this construction:

KEY-UPDATE UPON EVERY ENCRYPTION. In Fig-

ure 3 we simply require the encryption algorithm E

to update the secret keys k

(u)

and k

(u)

(of targeted

receivers u) upon every invocation. This resolves the

center’s cumbersome management. This also reduces

the storage at the center, for the service provider needs

to save only the state s

(u)

and not these keys.

Updating the secret keys on each encryption may

seem to increase the computational overhead at the

center, but this increase is cancelled by the replace-

ment of

E with XOR (⊕); note that since the keys

for

E are now updated each time,

E need to be only

one-time secure.

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

144

INTRODUCTION OF KEYED HASH-FUNCTION H.

The hash function H : {0, 1}

× {0, 1}

∗

→ {0, 1}

in Figure 3 reduces the center’s overhead in comput-

ing tags. H is keyed with a (fresh, random) session-

key K

, which is common to all receivers.

“MAC-THEN-MAC” STRUCTURE. We use two

MACs in Figure 3. The external MAC

T uses a con-

stant, long-lived secret key s

(u)

, and the internal MAC

T : {0, 1}

×{0, 1}

∗

→ {0, 1}

uses a key k

(u)

that

is updated via G periodically (upon every encryption).

The external MAC

T gets around with the DoS attack

and enables us to omit the stage number i

(u)

, while

the internal MAC T assures forward security and en-

ables us to use a common counter ctr. So this “MAC-

then-MAC” mechanism doubles the size of tag but

keeps minimal the increase in the header size. Also

note that these MACs T and

T now have ﬁxed-size

inputs, owing to the hash function H. In Section 6 it

will become clear why the usage of constant key for

the outer MAC still guarantees forward security.

STORAGE SIZE. Figure 4 shows the storage at the

center. Note that the increase is just ctr, under the

assumption



ctr

(u)



(u)



ctr

(u)

Figure 4: Storages with the improved construction.

5 ALGORITHM DESCRIPTION

Our authenticated-encryption scheme AE, based on

the improved construction in Section 4, is encapsu-

lated into three algorithms as AE = (S, E, D). In

this section we give precise deﬁnitions of these algo-

rithms.

STATE GENERATION ALGORITHM. S is a probabilis-

tic algorithm that takes as its input the set U of all

users

and outputs the initial state S = (ctr, ~s) ←

S(U ), where ctr is the state information common to

all users (i.e., the counter) and~s = (s

(u)

)

u∈U

the vec-

tor of users’ secret information. We use the notation

(u)

= (ctr, s

(u)

), and the state S

(u)

is distributed to

the user u prior to transmission of data.

Algorithm S(U )

ctr ← 0;

(u)

← {0, 1}

+κ

for each u ∈ U ;

~s ← (s

(u)

)

u∈U

; S ← (ctr, ~s)

Return S

For simplicity we ﬁx the set U of all users, but in prac-

tice a new user can be freely joined at any time during the

service.

ENCRYPTION ALGORITHM. E is invoked by the cen-

ter. E is a probabilistic and stateful algorithm that

takes as its input the current state S

(which con-

tains the counter plus all users’ secret information),

a recipient list P and a plaintext m, and that out-

puts (S

i+1

, C) ← E(S

, P, m). S

i+1

denotes the next

state. C denotes the encrypted data (c,

h), where c is

the common ciphertext and

h = (h

(u)

)

u∈P

the header

vector. We use the notation C

(u)

= (c, h

(u)

). Upon

receiving C = (c,

h), each user u parses the data and

retrieves C

(u)

. The user u is concerned about conﬁ-

dentiality and integrity of data C

(u)

only (and not the

entire C).

Algorithm E(S, P, m)

← {0, 1}

; ˆc ← E

(m);

(ctr, ~s) ← S; ctr ← ctr + 1; K

← {0, 1}

;

d ← H

(ˆckctr); c ← ˆckctrkK

For each u ∈ P do:

Parse s

(u)

= s

(u)

;

(u)

, k

(u)

, k

(u)

) ← G(s

(u)

); s

(u)

← s

(u)

;

(u)

← k

(u)

⊕ K

; v

(u)

← dkK

(u)

;

tag

(u)

← T

(u)

);

tag

(u)

←

(u)

ktag

(u)

);

(u)

←

(u)

ktag

(u)

tag

(u)

EndFor

~s ← (s

(u)

)

u∈P

; S ← (ctr, ~s );

h ← (h

(u)

)

u∈P

; C ← (c,

Return (S, C)

DECRYPTION ALGORITHM. D is associated with

each user u. D is a deterministic and stateful algo-

rithm that takes as its input u ’s current state S

(u)

and

received ciphertext C

(u)

, and outputs (S

(u)

i+1

, m) ←

D(S

(u)

, C

(u)

). D outputs m = ⊥ when rejecting

(u)

and m =y when detecting packet loss. In these

cases the state does not get updated; i.e., S

(u)

i+1

= S

(u)

Otherwise, D outputs the next state S

(u)

i+1

and the

plaintext m.

Algorithm D(S

(u)

, C

(u)

)

(ctr, s

(u)

) ← S

(u)

; Parse s

(u)

= s

(u)

;

(c, h

(u)

) ← C

(u)

Parse h

(u)

ktag

(u)

tag

(u)

Parse c = ˆckctr

′

; d ← H

(ˆckctr

′

);

(u)

← dkK

(u)

;

tag

′(u)

←

(u)

ktag

(u)

);

′(u)

, k

(u)

, k

(u)

) ← G(s

(u)

);

tag

′(u)

← T

(u)

)

If ctr

′

≯ ctr or tag

′(u)

6= tag

(u)

then return (S

(u)

, ⊥)

FORWARD-SECURE AUTHENTICATED-ENCRYPTION IN MULTI-RECEIVER SETTING

145

Else

If tag

′(u)

6= tag

(u)

then return (S

(u)

, y)

Else

← k

(u)

⊕

(u)

; m ← E

−1

(ˆc);

′(u)

← s

′(u)

(u)

; S

′(u)

← (ctr

′

, s

′(u)

)

Return (S

′(u)

, m)

EndIf

CONSISTENCY REQUIREMENTS. Initialize the state

as S

← S. For a sequence (P

, m

), . . . , (P

, m

)

set (S

i+1

, C

) ← E(S

, P

, m

) for i = 0, . . . , n.

For u ∈ U let i

(u)

, i

(u)

, . . . denote the indices of

P to which u belongs, in increasing order. Set

′

← S

and (S

′(u)

j+1

, m

′(u)

) ← D(S

′(u)

, C

(u)

) for

j = 0, 1, . . .. We require the soundness conditions

as follows: For all u and j such that u ∈ P

(u)

the

condition m

′(u)

= m

(u)

must hold. Also, for all

u and j < j

′

such that u ∈ P

(u)

, P

(u)

′

the condi-

tions (S

′(u)

′

, ⊥) = D(S

′(u)

′

, C

(u)

) and (S

′(u)

, y) =

D(S

′(u)

, C

(u)

′

) must hold.

6 SECURITY DEFINITIONS

In the following we describe the adversarial models

we adopt in our security analysis.

CONFIDENTIALITY. (Bellare and Yee, 2003) dis-

cussed the forward security of symmetric-key encryp-

tion and introduced an adversarial model based on

ﬁnd-then-guess indistinguishability. However, this

adversarial model is not amenable to our stateful en-

cryption, for in our case each state is used only once

to encrypt a single message and never used again to

encrypt another one. So instead we adopt the secu-

rity notion real-or-random indistinguishability (Bel-

lare et al., 1997) and modify it into the form of for-

ward security. This is essentially modeled on the

notion of forward-secure PRNGs (Bellare and Yee,

2003).

We modify the adversarial model into a form that

accords to multi-receiver settings. Namely, for a chal-

lenge bit b ∈ {0, 1} and an adversary A attacking

an authenticated-encryption scheme AE = (S, E, D),

we consider the following experiment:

Experiment Exp

fsind-cpa-b

(A)

S ← S

Run A

(·,·)

Reply to O

(P, m

) as follows:

Again, it sufﬁces to consider only the chosen-plaintext

attacks here.

If A ∈ P then

(S, C) ← E(S, P, m

); A ⇐ C EndIf

If A /∈ P then m

← {0, 1}

;

(S, C) ← E(S, P, m

); A ⇐ C EndIf

Until A outputs intrude

A ⇐ S

(u)

for each u ∈

P ;

b ← A

Return

In the above experiment, queries with A ∈ P are al-

ways answered with real, and those with A /∈ P are

answered with real or random, depending on the value

b. At the end of queries to O, the adversary A outputs

intrude and is fed with the current state S

(u)

of users

u ∈

P . We assume that A’s access set

P , such that

P ⊂

P for all queries (P, m

), is known a priori.

We then measure the adversary A’s advantage via

Adv

fsind-cpa

(A) = Pr

Exp

fsind-cpa-1

(A) = 1

− Pr

Exp

fsind-cpa-0

(A) = 1

Also we deﬁne the advantage function as

Adv

fsind-cpa

(t, q

, q

out

, µ, π) = max

Adv

fsind-cpa

(A),

where the maximum is taken over all adversaries A

with time complexity at most t (including its code

size), each making at most q

queries to the O ora-

cle with A ∈ P and q

out

with A /∈ P , with each m

being at most µ bits and the cardinality of

P being at

most π.

INTEGRITY. We basically adopt the strongest

“Type5” integrity notion (Kohno et al., 2003), with

an enhancement for packet-loss detection. We shall

modify the adversarial model into the form of forward

security (Bellare and Yee, 2003) and multi-receiver

setting:

Experiment Exp

fsint-ctxt

(A)

S ← S; S

′

← S; S

′′

← S

(u)

)

u∈U

←

0; (i

′(u)

)

u∈U

←

0; (i

′′(u)

)

u∈U

←

Run A

(·,·),O

−1

′

(·,·)

(before)

Reply to O

(P, m) as follows:

(S, C) ← E(S, P, m);

(u)

← i

(u)

+ 1 for each u ∈ P ;

(u)

← C

(u)

for each u ∈ P ; A ⇐ C

Reply to O

−1

′

(u,

(u)

) as follows: # u 6= A

′

(u)

, m) ← D(S

′

(u)

)

If m 6= ⊥, y and (i

′(u)

+ 1 > i

(u)

6= C

(u)

′(u)

) then return 1 EndIf

If m =y and (i

′(u)

+ 2 > i

(u)

/∈ {C

(u)

′(u)

, . . . , C

(u)

}) then

return 1 EndIf

If m 6= ⊥, y then i

′(u)

← i

′(u)

+ 1; A ⇐ 1

Else A ⇐ 0 EndIf

Until A outputs intrude

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

146

A ⇐ S

(u)

for each u ∈

Run A

−1

′′

(·,·)

(after)

Reply to O

−1

′′

(u,

(u)

) as follows: # u 6= A

′′(u)

, m) ← D(S

′′(u)

(u)

)

If i

′′(u)

+ 1 ≤ i

(u)

and m 6= ⊥, y and

(u)

6= C

(u)

′′(u)

then return 1 EndIf

If m 6= ⊥, y then i

′′(u)

← i

′′(u)

+ 1; A ⇐ 1

Else A ⇐ 0 EndIf

Until A halts

Return 0

In the above experiment we assume that A’s access

set

P (such that P ⊂

P and u ∈

P for all queries

(P, m) and (u,

(u)

)) is known a priori. A’s goal in

the before stage is to forge a (new) ciphertext that is

either accepted or considered as a valid, future cipher-

text by the decryption oracle. At the end of before

stage A outputs intrude (thereby giving up forging in

the before stage) and is fed with the current state S

(u)

of users u ∈

P . Then the state of each u’s decryption

oracle is rewound to its initial value, and the game

resumes in after stage. Note that at this point A can

freely forge future ciphertexts at stages after the intru-

sion, so now A’s goal is to forge a new ciphertext that

is accepted by the decryption oracle at a stage before

the intrusion.

We measure the adversary A’s advantage via

Adv

fsint-ctxt

(A) = Pr

Exp

fsint-ctxt

(A) = 1

Also we deﬁne the advantage function as

Adv

fsint-ctxt

(t, q

enc

, q

before

, q

after

, µ, π)

= max

Adv

fsint-ctxt

(A),

where the maximum is taken over all adversaries A

with time complexity at most t (including its code

size), each making at most q

enc

queries to the O or-

acle, q

before

queries to the O

−1

oracle in before stage

for each u and q

after

queries to the O

−1

oracle in after

stage for each u, with each m and ˜c (the ciphertext

part of

(u)

) being at most µ bits and the cardinality

P being at most π.

SECURITY OF EACH PRIMITIVE. We quickly review

the security deﬁnitions for the cryptographic primi-

tives used in our construction. For a symmetric-key

cipher E : {0, 1}

× {0, 1}

∗

→ {0, 1}

∗

deﬁne

Experiment Exp

ind-cpa-b

(A)

← {0, 1}

Run A

(·)

Reply to O

) as follows:

← {0, 1}

; c ← E

); A ⇐ c

Until A returns a bit

Return

Adv

ind-cpa

(A) = Pr

Exp

ind-cpa-1

(A) = 1

− Pr

Exp

ind-cpa-0

(A) = 1

Adv

ind-cpa

(t, q, µ) = max

Adv

ind-cpa

(A),

where the maximum is taken over all adversaries A

with time complexity at most t, each making at most

q queries to the O oracle and each m being at most µ

bits.

For a PRNG G : {0, 1}

→ {0, 1}

+κ

deﬁne

Experiment Exp

prg-b

(A)

← {0, 1}

+κ

; s

← {0, 1}

;

← G(s); A ⇐ x

;

b ← A

Return

Adv

prg

(A) = Pr

Exp

prg-1

(A) = 1

− Pr

Exp

prg-0

(A) = 1

Adv

prg

(t) = max

Adv

prg

(A),

where the maximum is taken over all adversaries A

with time complexity at most t.

For a keyed hash-function H : {0, 1}

{0, 1}

∗

→ {0, 1}

, deﬁne

Experiment Exp

tcr

(A)

m ← A; K

← {0, 1}

; d ← H

(m);

A ⇐ (K, d); m

′

← A; d

′

← H

′

)

If m

′

6= m and d

′

= d then return 1

Else return 0 EndIf

Adv

tcr

(A) = Pr



Exp

tcr

(A) = 1



Adv

tcr

(t, µ) = max

Adv

tcr

(A),

where the maximum is taken over all adversaries A

with time complexity at most t and with m, m

′

being

at most µ bits.

For a MAC T : {0, 1}

× {0, 1}

→ {0, 1}

with ﬁxed-size input, deﬁne

Experiment Exp

suf-cma

(A)

← {0, 1}

; L ← ∅

Run A

(·),O

−1

(·,·)

Reply to O

(m) as follows:

tag ← T

(m); L ← L ∪ (m, tag); A ⇐ tag

Reply to O

−1

(m, tag) as follows:

If (m, tag) /∈ L and tag = T

(m) then

return 1 Else A ⇐ 0 EndIf

Until A halts

Return 0

Adv

suf-cma

(A) = Pr

Exp

suf-cma

(A) = 1

Adv

suf-cma

(t, q

enc

, q

dec

) = max

Adv

suf-cma

(A),

FORWARD-SECURE AUTHENTICATED-ENCRYPTION IN MULTI-RECEIVER SETTING

147

where the maximum is taken over all adversaries A

with time complexity at most t, each making at most

enc

queries to the O oracle and q

dec

queries to the

−1

oracle.

7 SECURITY OF PROPOSED

SCHEME

For conﬁdentiality we have

Adv

fsind-cpa

(t, q

, q

out

, µ, π) ≤

8π · (q

+ q

out

) · Adv

prg

(t)

+ q

out

· Adv

ind-cpa

(t + q

· O(E(1

)), 1, µ),

and for integrity

Adv

fsint-ctxt

(t, q

enc

, q

before

, q

after

, µ, π) ≤

π · Adv

prg

(t + q

enc

· O(G)) + q

enc

· Adv

tcr

(t, µ)

+ πq

enc

· Adv

suf-cma

(t + q

enc

· O(G), 1, q

after

)

+ π · Adv

suf-cma

(t, q

enc

, q

before

The proof can be done in a standard hybrid argument.

Due to space limitation, we omit the detailed proofs

here. Note that our security reduction is in the con-

crete security model, with the adversary’s resources

being quantiﬁed.

8 PRACTICAL INSTANTIATION

PRODUCING K

AND K

. The random variables

and K

can be generated by using a (for-

ward secure) PRNG, provided that the secrecy of the

seed/state is kept exclusively by the service provider.

The security analysis can be conducted similarly

when these two variables are replaced with pseudo-

random bits.

INSTANTIATION OF KEYED HASH-FUNCTION H. In

the recent work (Halevi and Krawcyzk, 2006) a new

mode of operation for (keyless) hash function is pro-

posed, which yields a target-collision-resistant hash-

function with constant-sized keys for arbitrary long

messages. So H can be instantiated with a keyless

hash-function like SHA256 running in this mode.

9 CONCLUSION

In this paper we have explored the problem of DoS

attack in forward-secure authentication in unidirec-

tional, multi-receiver scenario. We have provided the

“MAC-then-MAC” structure which resists against the

DoS attack and can be combined with the straight-

forward method of key distribution. It remains an

interesting work to investigate other constructions of

forward-secure authenticated-encryption that can be

combined with more efﬁcient schemes.

REFERENCES

Bellare, M., Desai, A., Jokipii, E., and Rogaway, P. (1997).

A concrete security treatment of symmetric encryp-

tion. In Proceedings of the 38th Symposium on Foun-

dations of Computer Science, pages 394–403. IEEE

Computer Soceity Press.

Bellare, M. and Namprempre, C. (2000). Authenticated en-

cryption: Relations among notions and analysis of the

generic composition paradigm. In Okamoto, T., edi-

tor, Advances in Cryptology – ASIACRYPT 2000 Pro-

ceedings, volume 1976 of Lecture Notes in Computer

Science, pages 531–545. Springer-Verlag.

Bellare, M. and Yee, B. S. (2003). Forward-security in

private-key cryptography. In Joye, M., editor, Topics

in Cryptology – CT-RSA 2003 Proceedings, volume

2612 of Lecture Notes in Computer Science, pages 1–

18. Springer-Verlag.

Golle, P. and Modadugu, N. (2001). Authenticating

streamed data in the presence of random packet loss.

In Network and Distributed System Security Sympo-

sium 2001 Proceedings, pages 13–22. ISOC.

Halevi, S. and Krawcyzk, H. (2006). Strengthening digital

signatures via randomized hashing. To appear in Ad-

vances in Cryptology – CRYPTO 2006 Proceedings.

Kohno, T., Palacio, A., and Black, J. (2003). Building se-

cure cryptographic transforms, or how to encrypt and

MAC. Cryptology ePrint Archive, Report 2003/177.

http://eprint.iacr.org/.

Naor, D., Naor, M., and Lotspiech, J. (2001). Revocation

and tracing schemes for stateless receivers. In Kilian,

J., editor, Advances in Cryptology – CRYPTO 2001

Proceedings, volume 2139 of Lecture Notes in Com-

puter Science, pages 41–62. Springer-Verlag.

Park, J. M., Chong, E. K. P., and Siegel, H. J. (2002).

Efﬁcient multicast packet authentication using signa-

ture amortization. In Proccedings of the 2002 IEEE

Symposium on Security and Privacy, pages 227–240.

IEEE Computer Society.

Ray, I., Kim, E., McConnell, R., and Massey, D. (2005). Re-

liably, securely and efﬁciently distributing electronic

content using multicasting. In Bauknecht, K., Pr

oll,

B., and Werthner, H., editors, EC-Web 2005 Proceed-

ings, volume 3590 of Lecture Notes in Computer Sci-

ence, pages 327–336. Springer-Verlag.

Wong, C. K., Gouda, M., and Lam, S. S. (2000). Secure

group communications using key graphs. IEEE/ACM

Transactions on networking, 8(1):16–30.

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

148