
PRIVATE BIDDING FOR MOBILE AGENTS
Bartek Gedrojc, Kathy Cartrysse, Jan C. A. van der Lubbe
Delft University of Technology
Mekelweg 4, 2628 CD, Delft, the Netherlands
Keywords:
Untrustworthy Environments, Oblivious Third Party, Φ-Hiding Assumption, ElGamal, Mobile Software
Agents, Multi-Party Computation.
Abstract:
A major security and privacy threat for Mobile Software Agents are Untrustworthy Environments; which are
able to spy on the agents’ code and private data. By combining Multi-Party Computation with ElGamal public-
key encryption system we are able to create a protocol capable of letting two agents have a private bidding
within an Honest-but-Curious environment only with the help of an Oblivious Third Party. The Oblivious
party is able to compare two encrypted inputs without being able to retrieve any information about the inputs.
1 INTRODUCTION
In this vast growing digital era we are more often sur-
rounded by intelligent devices which can support us
in our daily life. While information flows through
these ambient devices, which are not only connected
to local networks but also to the outside world, we
can expect to encounter security and privacy threats.
The most alarming threat is the malicious user who
has the ability to create malicious agents, spy on in-
secure communication channels but also to create un-
trustworthy environments (Claessens et al., 2003).
Every environment has total control over the infor-
mation that is executed in his digital “world” and it
can therefore manipulate the agent code. One topic
that so far received relatively little attention in lit-
erature is the execution of mobile software agents
within untrustworthy environments. Most research
focusses on malicious agents and communications,
and assumes the agents are executed in trusted envi-
ronments.
Mobile software agents may possess private infor-
mation of their user e.g. credit card numbers, personal
preferences, etc. Agents should be able to perform
tasks on behalf of their users by using this personal
information within untrustworthy environments with-
out compromising security and privacy.
One of the solutions to the untrustworthy environ-
ments problem is Execution Privacy, which strives to
the correct execution of software agents while keep-
ing the agent code and state private
In section 2 we present our model and we will dis-
cuss the relation between previous work. Section 3
describes the building blocks that are necessary to
construct the protocol. In section 4 the protocol is
presented, while section 5 discusses the security of
the protocol. Finally, section 6 ends with concluding
remarks.
2 PROBLEM DESCRIPTION
This paper addresses the private bidding problem
which was introduced by (Cachin, 1999): Alice wants
to buy some goods from Bob if the price is less than
a and Bob would like to sell, but only for more than b
and neither of them wants to reveal the secret bounds.
Our objective is to demonstrate that private bidding is
also feasible with Mobile Software Agents while this
bidding takes places in an untrustworthy environment.
To achieve this goal we are using an Oblivious Third
Party to compare the bids of Alice and Bob without
learning any information about a or b.
2.1 Model
Our private bidding for mobile agent model is almost
similar to the original private bidding model as was
described by (Cachin, 1999). Only, in our case the
277
Gedrojc B., Cartrysse K. and C. A. van der Lubbe J. (2006).
PRIVATE BIDDING FOR MOBILE AGENTS.
In Proceedings of the International Conference on Security and Cryptography, pages 277-282
DOI: 10.5220/0002102702770282
Copyright
c
SciTePress

communication between the Agents (bidders) is done
in an untrustworthy environment i.e. public environ-
ment instead of a private environment. Therefore, we
must make sure that the communication between the
agents and the final decision on who has the highest
bid remains secure and private, even if this takes place
in an untrustworthy environment, see Figure 1.
OTP
OTP
Figure 1: Private Bidding Scenario.
Alice (A), Bob (B) and the Oblivious Third Party
(OTP) are the three parties involved in the model.
Also, Alice and Bob are mobile software agents who
share some random secret with each other. The OTP
is a trusted party that will correctly execute the inputs
a, b given by Alice or Bob, without being able to learn
any information about the inputs. The goal of Alice
and Bob is to determine if a > b. In an e-commerce
setting this means that the maximum price the buyer
(Alice) is willing to pay is greater than the minimum
price the seller (Bob) is willing to receive. Besides
this, they will only reveal their actual bids a, b if it
satisfies the a > b condition, otherwise they will keep
their secrets private.
Our agent bidding model is situated in an untrust-
worthy environment. Due to the hardness of the prob-
lem we assume that this environment will execute the
agents and the code correctly, but it is interested in
what it is processing. This implies that the agents are
not able to use their private keys or any other secret
data. Therefore, we will use the OTP to perform the
comparison of the inputs without revealing it to the
untrustworthy environment.
The Untrustworthy Environment is also called an
honest-but-curious adversary which was introduced
by (Rabin, 1981). Consequently, the environment
is a server executing the mobile code i.e. the mo-
bile agent, while storing all information from the
agents and all communication between the agents.
The server is not a Malicious Environment trying to
modify the mobile code. Our goal is to ensure the
server does not learn the private inputs a, b before the
agents decide privately to reveal their secret inputs
e.g. when the bidding satisfies a > b.
2.2 Contribution
We present a Private Bidding protocol for Mobile
Software agents while these agents are situated in
an Honest-but-Curious environment only by using an
Oblivious Third Party. Our solution mixes the Private
Agent Communication algorithm from (Cartrysse,
2005; Cartrysse and van der Lubbe, 2004) with the
Private Bidding protocol from (Cachin, 1999).
With our contribution we demonstrate that it is pos-
sible to have a secure, efficient and fair private bid-
ding protocol for mobile software agents. Applica-
tions can be found in e-commerce scenarios where the
bidding takes place on a public server and where the
user has no communication with his mobile software
agents.
2.3 Related Work
Private bidding originates from the Millionaires’
problem initially described by (Yao, 1982). Fur-
ther research proved that any multi-party function can
be computed securely even without the help from
a third party (Goldreich, 2002). But, according
to (Algesheimer et al., 2001) secure mobile agents
schemes do not exist when some environment is to
learn information that depends on the agent’s current
state. Therefore, in order to merge mobile agents
with multi-party computation techniques we needed
the help of an Oblivious Third Party.
The concept of combining mobile agents and
making decisions in the encrypted domain origi-
nates from (Sander and Tschudin, 1998a; Sander
and Tschudin, 1998b). They proposed a software
only non-interactive computing with encrypted func-
tions which was based on homomorphic encryption
schemes. We elaborate on their concept by using (El-
Gamal, 1984) as the basis of our agent communica-
tion algorithm. We also manifest that the ElGamal
encryption in our model can be used with the homo-
morphic in addition property without loosing security.
The Non-Interactive CryptoComputing for N C
1
by (Sander et al., 1999) also discusses computing
with encrypted functions w.r.t. mobile agent systems.
Their solution is capable of comparing two private in-
puts but it does not provide fairness because the inputs
must be encrypted by one of the agents’ public keys.
Consequently, the results will only be available to one
of agents. Also, the private key to decrypt the result of
the comparison cannot be used in the untrustworthy
environment and therefore the agent must leave this
environment to learn the result of the computation.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
278
3 BUILDING BLOCKS
Before discussing the private bidding protocol in
paragraph 4 we will elaborate more on the crypto-
graphic techniques which we have used.
3.1 Φ-Hiding Assumption
Our model is based on the Φ-Hiding Assumption (Φ-
HA) published by (Cachin et al., 1999), which states
the difficulty of deciding whether a small prime di-
vides φ(m), where m is a composite integer of un-
known factorization. We use the Φ-HA as follows:
Choose randomly m that hides a prime p
0
so it is hard
to distinguish if p
0
or p
1
is a factor of φ(m), where p
1
is randomly and independent chosen i.e. it is compu-
tationally indistinguishable.
Let us choose m = p
′
q
′
where p
′
is a safe prime
(prime p is a safe prime if
p−1
2
is also a prime) and q
′
is a quasi-safe prime. We compute p
′
= 2q
1
+ 1 and
q
′
= 2pq
1
+ 1, where q
1
is a prime and p, q
2
are odd
primes.
The Euler totient function φ(m) is defined as the
number of positive integers ≤ m which are relative
prime to m. This results in the Euler totient theorem
g
φ(m)
≡ 1 mod m
(1)
where g ∈ Z. Next, we compute the Euler totient
function:
φ(m) = φ(p
′
q
′
) = (p
′
− 1)(q
′
− 1)
= (2q
1
+ 1 − 1)(2pq
1
+ 1 − 1)
= (2q
1
)(2pq
2
) = 4pq
1
q
2
(2)
Combining (1) and (2) we can compute:
g
4pq
1
q
2
≡ 1 mod m
(3)
Given a set of primes P = {p
1
, . . . , p
n
} where n ≥ 0
we can compute
Q
n
i=0
p
i
. Also, by computing m that
hides a prime p we can use the Φ-HA to determine if
P contains a p-th root module m using the factoriza-
tion of m. To perform this check one computes
g
4pq
1
q
2
p
n
i=0
p
i
≡ 1 mod m
(4)
if it is congruent to 1 modulo m then the set P hides
p else is does not. Note that m hides p if and only
if p|φ(m). It is important that the g ∈ Z should not
be a p-th root module m i.e. there exists no µ such
that µ
p
≡ g mod m. Therefore, we should choose
g ∈ QR
m
because p should not be an even prime.
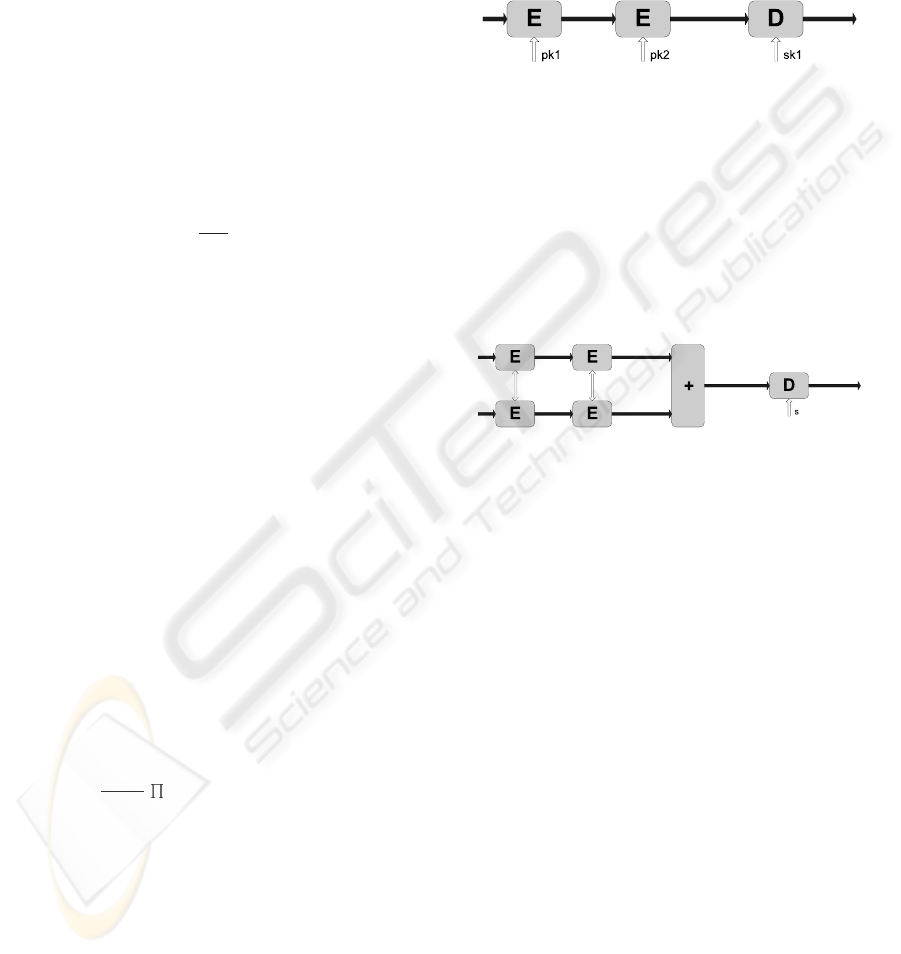
3.2 Homomorphic E-E-D
In (Cartrysse and van der Lubbe, 2004) an algorithm
is described that is able to encrypt a message m with
the key of Alice and send it to Bob who encrypts the
message again with his own key. Resulting in the
message to be send back to Alice, who will be able
to decrypt the message and be left with the message
encrypted by Bob. This algorithm, as visualized in
Figure 2 is know as E-E-D (Encryption-Encryption-
Decryption).
x
E
pk1
(x) E
pk2
(E
pk1
(x)) E
pk2
(x)
Figure 2: E-E-D model.
Our private bidding model uses this E-E-D prop-
erty, as well as the homomorphic addition based on
ELGamal encryption (ElGamal, 1984). The idea be-
hind the model is to encrypt two messages with differ-
ent keys and add them together. Next, the messages
are decrypted with the first key and the result will be
the addition of the two messages which are only en-
crypted with the second key, see Figure 3.
x
1
E
pk1
(x
1
) E
pk2
(E
pk1
(x
1
))
pk1 pk2
E
pk1
(x
2
) E
pk2
(E
pk1
(x
2
))
E
pk2
(x
1
+x
2
)
k1
x
2
E
pk2
(E
pk1
(x
1
+x
2
))
Figure 3: Homomorphic E-E-D in Addition model.
We generate a large prime p and a generator g ∈
Z
∗
p
. We choose a random integer a
1
, 1 ≤ a
1
≤ p − 2
and compute ω = g
a
1
mod p. We also need to select
a random integer k
1
, 1 ≤ k
1
≤ p − 2 and compute the
following
γ
1
= g
k
1
mod p
δ
1,x
1
= x
1
ω
k
1
mod p
The public key (pk1) is (p, g, ω
1
), the message is
x
1
, the cipher text is c
1,x
1
= (γ
1
, δ
1,x
1
) and the secret
key (sk1) is a
1
. Next we can encrypt δ
1,x
1
, using a
new public key ω
2
but with the same generator g and
prime p. We must also compute ω
2
= g
a
2
mod p and
use this to encrypt the message using the following
γ
2
= g
k
2
mod p
δ
2,x
1
= δ
1,x
1
ω
k
2
2
mod p = x
1
ω
k
1
1
ω
k
2
2
mod p
The public key (pk2) is (p, g, ω
2
), the cipher text
is c
2,x
1
= (γ
1
, δ
2,x
1
) and the secret key (sk2) is
a
2
. For convenience we can write the above steps
as E
pk2
(E
pk1
(x
1
)) which represent the top left two
function blocks from Figure 3.
We also want to encrypt a message x
2
with the
same keys and the same random integers k
1
, k
2
as
PRIVATE BIDDING FOR MOBILE AGENTS
279

message x
1
, which can be calculated as above. We
can write this result as E
pk2
(E
pk1
(x
2
)) which repre-
sents the two bottom left function blocks from Figure
3. Next we can add the two encrypted messages δ
2,x
1
,
δ
2,x
2
using the homomorphic property of ElGamal as
follows
δ
2,x
1
+ δ
2,x
2
= δ
1,x
1
ω
k
2
2
mod p + δ
1,x
2
ω
k
2
2
mod p
= x
1
ω
k
1
1
ω
k
2
2
mod p + x
2
ω
k
1
1
ω
k
2
2
mod p
= (x
1
+ x
2
)ω
k
1
1
ω
k
2
2
mod p
= δ
2,x
1
+x
2
= x
The two encrypted messages δ
2,x
1
, δ
2,x
2
can only
be added to one another when they are both encrypted
with the same public keys and with the same k
1
, k
2
.
The result is E
pk2
(E
pk1
(x
1
+ x
2
)) and can be de-
crypted using the first private key a
1
and the follow-
ing formula
x
′
= D
sk1
(x) =
δ
2,x
1
+x
2
γ
a
1
1
mod p
=
(x
1
+ x
2
)ω
k
1
1
ω
k
2
2
g
k
1
a
1
mod p
= (x
1
+ x
2
)ω
k
2
2
mod p
We now have the first and the second message
added to one another and encrypted with the second
public key pk2, which can be written as
D
sk1
(E
pk2
(E
pk1
(x
1
+ x
2
))) = E
pk2
(x
1
+ x
2
) = x
′
Consequently, decrypting x
′
produces the following
D
sk1
(x
′
) =
x
′
γ
a
2
2
mod p
=
(x
1
+ x
2
)ω
k
2
2
g
k
2
a
2
mod p
= x
1
+ x
2
which is the addition of the two messages without en-
cryption (plaintext).
It has to be noticed that according to the
Diffie-Hellman problem it is impossible to compute
g
ak
mod p from g
a
mod p and g
k
mod p (Diffie and
Hellman, 1976). This means that the key a and the
random integer k must remain secure, and prefer-
ably be changed frequently. We have chosen to make
a double encryption by one user using an equal k,
because otherwise we cannot use the homomorphic
property in addition of the ElGamal encryption. A se-
curity evaluation will follow in paragraph 5 concern-
ing the use of this identical k.
4 PROTOCOL
The protocol starts by letting the Oblivious Third
Party (OTP) generate an ElGamal key-pair with the
public-key E
pkt
and the secret-key D
skt
.
The buyer Alice does not want to spend more than
her maximum amount a, which can be represented as
a binary string. She also chooses random and inde-
pendent values x
l
, x
l−1
, . . . , x
0
∈ Z, r
l−1
, . . . , r
0
∈
Z and s
l−1
, . . . , s
0
∈ Z, where l is the amount of bits
needed for a and b, and where b is the minimum price
of Bob the seller.
Alice needs to define an n-bit prime p
a
= λ(t
a
)
where t
a
∈ {0, 1}
n
is randomly chosen. Using λ(x)
she can map a string x to an n-bit prime p e.g. by
finding the smallest prime greater than x. Then Alice
generates a random m
A
using the Φ-Hiding Assump-
tion, as described above, which hides her prime p
a
.
She also computes G
a
=
φ(m
a
)
p
a
which is kept secret
from the OTP.
Next, a key κ for the hash function H
κ
must be
generated and published. Then Alice needs to calcu-
late ϕ
a,j
using the hash function H
κ
(x
j
+ s
j
) and
compute the following for j = l − 1, . . . , 0
ϕ
a,j
= H
κ
(x
j
+ s
j
) ⊕ t
a
Alice also needs to encrypt the input string a
j
using
her public-key E
pka,j
and random integers k
a,j
for
j = l − 1, . . . , 0. This has to be “sealed” using the
public-key of the OTP and the random integers k
t,j
y
a,j
=
E
pkt,j
(E
pka,j
(x
j
− x
j+1
+ r
j
))
E
pkt,j
(E
pka,j
(x
j
− x
j+1
+ s
j
+ r
j
))
if a
j
= 0
if a
j
= 1
The bidding is prepared for Bob by Alice using the
same cryptosystem with random integers k
t,j
, k
a,j
and public-keys E
pkt,j
y
b,j
=
y
b0,j
= E
pkt,j
(E
pka,j
(−r
j
))
y
b1,j
= E
pkt,j
(E
pka,j
(−s
j
− r
j
))
if b
j
= 0
if b
j
= 1
She also computes
Ψ
b,j
= H
κ
(x
j
− s
j
)
and sends it to Bob.
Bob is able to acquire the public y
b0,j
, y
b1,j
and
compute according his own input string b
j
, y
b,j
. Be-
cause y
a,j
is also publicly available he can compute
y
ab,j
using
y
ab,j
= y
a,j
+ y
b,j
(5)
To be sure that the Untrustworthy Environment will
not be able to construct b from y
ab
Bob has to encrypt
(5) again, by computing
w
ab,j
= E
pkt,j
(y
ab,j
)
The only requirement is that Bob uses the same cryp-
tosystem as Alice is using, in other words he has to
use the same generator g and prime p but he can use a
different k.
Bob has already chosen a t
b
∈ {0, 1}
n
, defined
an n-bit prime p
b
= λ(t
b
) and generated a random
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
280

m
b
. He also computes G
b
=
φ(m
b
)
p
b
and keeps this
secret from the OTP. Bob receives from Alice Ψ
a,j
and computes before entering the environment for
j = l − 1, . . . , 0
ϕ
b,j
= Ψ
a,j
⊕ t
b
Alice and Bob have prepared their bidding using
the public information and are now able to move into
the Untrustworthy Environment. Then Bob sends
ϕ
b,j
, m
b
and w
ab,j
to Alice.
Alice is able to decrypt w
ab,j
because she is in pos-
session of the secret-key D
ska,j
z
j
= D
ska,j
(w
ab,j
)
= D
ska,j
(E
pkt,j
(E
pkt,j
(E
pka,j
(y
ab,j
))))
= E
pkt,j
(E
pkt,j
(y
ab,j
))
The bidding is prepared and Alice sends
κ, x
l
, z
l−1
, . . . , z
0
, ϕ
a,l−1
, . . . , ϕ
a,0
ϕ
b,l−1
, . . . , ϕ
b,0
, m
a
, m
b
to the OTP.
The OTP makes c
l
= x
l
and chooses g
a,l
∈ QR
m
a
,
g
b,l
∈ QR
m
b
by selecting a random element of Z
m
a
,
respectively Z
m
b
, and squaring it. For j = l−1, . . . , 0
the following five steps are repeated
1.c
j
= c
j+1
+ D
skt,j
(D
skt,j
(z
j
))
2.q
a,j
= λ(H
κ
(c
j
) ⊕ ϕ
a,j
)
3.g
a,j
= (g
a,j+1
)
q
a,j
mod m
a
4.q
b,j
= λ(H
κ
(c
j
) ⊕ ϕ
b,j
)
5.g
b,j
= (g
b,j+1
)
q
b,j
mod m
b
After this iteration the OTP chooses r
a
∈ Z
m
a
,
r
b
∈ Z
m
b
randomly and independently, computing
h
a
= (g
a,0
)
r
a
h
b
= (g
b,0
)
r
b
where h
a
is send to Alice and h
b
is send to Bob.
Both agents can test the result given by the OTP
by using the factorization of m
a
and m
b
. Alice can
check if a > b
h
G
a
a
= h
φ(m
a
)
p
a
a
≡ 1 mod m
a
Similarly, Bob can check if a < b by computing
h
G
b
b
= h
φ(m
b
)
p
b
b
≡ 1 mod m
b
5 SECURITY
The original private bidding protocol by (Cachin,
1999) did not use ElGamal for the communication be-
tween the bidders. Our choice for ElGamal was de-
fined by the use of the E-E-D algorithm, which also
implies that we could not encrypt 0 because it did not
lie in the group. Therefore, we had to add an extra
parameter r
j
to solve this problem.
Secure: Our protocol is secure if the bidding takes
place in a honest-but-curious environment that does
not conspire with the OTP e.g. the environment
should not give the private-key of Alice to the OTP
which is used to decrypt w
ab,j
.
Private-key: The environment is able to spy on
the agents’ code and communication. Therefore it
possesses the private decryption key of Alice D
ska,j
.
This private-key is only known by the environment
and Alice, and should not be know by the OTP. This
is not a threat, because one of the constraints of the
model is that the OTP and the environment do not
conspire. Even, if the environment decrypts the in-
puts, it is still not able to recover the plaintext because
it needs the private-key of the OTP.
Conspire: The OTP and the environment should
not conspire otherwise the OTP is able to learn the pri-
vate inputs a, b of Alice and Bob. Using the private-
key of Alice, the OTP is able to learn the plaintext
content of y
a,j
and y
b,j
which are the transformed
private bids of the agents. To do so, he also needs
to know if y
b,j
corresponds with b
j
= 0 or b
j
= 1.
When the OTP possesses G
a
or G
b
, given by the
environment, then it is capable of checking after every
iteration in the final stage of the protocol when it con-
tains a p-th root modulo m
a
or m
b
. This means the
OTP will learn in which bit-position j the inputs a
and b are different for the first time. It will also know
that the bits before j are equal. Therefore, G
a
and G
b
should not be known to the OTP.
Fair: The protocol is fair because both Alice and
Bob are able to check individually what the result is
of the comparison computed by the OTP.
Efficient: While only having two messages be-
tween Alice and Bob and two messages between the
bidders and the OTP, we can say the protocol is ef-
ficient. The efficiency is gained by using an OTP
with standard cryptographic techniques instead of us-
ing circuits.
Random k: ElGamal is not secure if we us the ho-
momorphic in addition property, because we have to
keep the random k identical for every encryption. In
our case we also keep the k the same but we claim
this is secure. Alice is the only one who encrypts the
messages y
a,j
, y
b0,j
and y
b1,j
therefore she is the only
one who knows the content of the messages; which is
also not known to Bob. Suppose the same k is used to
encrypt two messages x
1
and x
2
and the result is the
ciphertext pairs (γ
1
, δ
1
) and (γ
2
, δ
2
). Then
δ
1
δ
2
=
x
1
x
2
(6)
is easily computed if x
1
or x
2
is known (Menezes
et al., 1996). In our case, the messages are only
PRIVATE BIDDING FOR MOBILE AGENTS
281

known to Alice and therefore no other entity is ca-
pable of computing (6). We therefore assume that the
use of the identical k does not make our model inse-
cure.
Cheating bidder: Alice initiates the private bid-
ding, therefore she can cheat the protocol. This could
be prevented by adding commitments and letting the
OTP be more actively involved in the bidding process.
If Bob would collude with the environment and get
access tot the private-key of Alice, he could use the
OTP as an oracle by querying it and gaining access to
her private data.
6 CONCLUSION
We have presented our private bidding protocol that
keeps the bids of the bidders private if the communi-
cation is executed in an honest-but-curious environ-
ment and where the involved parties do not collude
with one another. We have also seen that the system
crumbles if one of the parties is malicious, and manip-
ulates the data or communication. We have demon-
strated that private bidding is possible for mobile soft-
ware agents, but future work is needed to make the
system more resilient.
REFERENCES
Algesheimer, J., Cachin, C., Camenisch, J., and Karjoth, G.
(2001). Cryptographic security for mobile code. In
Proceedings of the IEEE Symposium on Security and
Privacy, page 2. IEEE Computer Society.
Cachin, C. (1999). Efficient private bidding and auctions
with an oblivious third party. In CCS ’99: Proceedings
of the 6th ACM conference on Computer and com-
munications security, pages 120–127, New York, NY,
USA. ACM Press.
Cachin, C., Micali, S., and Stadler, M. (1999). Compu-
tationally private information retrieval with polyloga-
rithmic communication. Lecture Notes in Computer
Science, 1592:402–414.
Cartrysse, K. (2005). Private Computing and Mobile Code
Systems. PhD thesis, Delft University of Technology.
Cartrysse, K. and van der Lubbe, J. (August 2004). Privacy
in mobile agents. First IEEE Symposium on Multi-
Agent Security and Survivability.
Claessens, J., Preneel, B., and Vandewalle, J. (2003). (how)
can mobile agents do secure electronic transactions on
untrusted hosts? a survey of the security issues and the
current solutions. ACM Trans. Inter. Tech., 3(1):28–
48.
Diffie, W. and Hellman, M. (1976). New directions in cryp-
tography. IEEE Transactions on Information Theory,
IT-22(6):644–654.
ElGamal, T. (1984). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. In Pro-
ceedings of CRYPTO 84 on Advances in cryptology,
pages 10–18. Springer-Verlag New York, Inc.
Goldreich, O. (2002). Secure multi-party computation. Fi-
nal (incomplete) Draft, Version 1.4.
Menezes, A., Vanstone, S., and Oorschot, P. v. (1996).
Handbook of Applied Cryptography. CRC Press, Inc.
Rabin, M. O. (1981). How to exchange secrets with obliv-
ious transfer. Cryptology ePrint Archive, Report
2005/187. http://eprint.iacr.org/.
Sander, T. and Tschudin, C. F. (1998a). Protecting mobile
agents against malicious hosts. Lecture Notes in Com-
puter Science, 1419:44–60.
Sander, T. and Tschudin, C. F. (1998b). Towards mobile
cryptography. In Proceedings of the IEEE Symposium
on Security and Privacy, Oakland, CA, USA. IEEE
Computer Society Press.
Sander, T., Young, A., and Yung, M. (1999). Non-
interactive cryptocomputing for NC 1. In IEEE Sym-
posium on Foundations of Computer Science, pages
554–567.
Yao, A. (1982). Protocols for secure computations. In
Carberry, M. S., editor, Proceedings of the 23rd An-
nual IEEE Symposium on Foundations of Computer
Science, Chicago IL, pages 160–164. IEEE Computer
Society Press.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
282
