
RANDOM SAMPLING ALGORITHMS FOR LANDMARK
WINDOWS OVER DATA STREAMS
Zhang Longbo, Li Zhanhuai,Yu Min, Wang Yong, Jiang Yun
School of Computer Science, Northwestern Polytechnical University, Xi’an, Shaanxi 710072, China
Keywords: Data stream, Landmark Window, Approximate algorithm, Random Sampling.
Abstract: In many applications including sensor networks, telecommunications data management, network monitoring
and financial applications, data arrives in a stream. There are growing interests in algorithms over data
streams recently. This paper introduces the problem of sampling from landmark windows of recent data
items from data streams and presents a random sampling algorithm for this problem. The presented
algorithm, which is called SMS Algorithm, is a stratified multistage sampling algorithm for landmark
window. It takes different sampling fraction in different strata of landmark window, and works even when
the number of data items in the landmark window varies dramatically over time. The theoretic analysis and
experiments show that the algorithm is effective and efficient for continuous data streams processing.
1 INTRODUCTION
1.1 Motivation
In many applications including sensor networks,
telecommunications data management, network
monitoring and financial applications, data does not
take the form of traditional stored relations, but
rather arrives in continuous, rapid, time-varying data
streams. Data streams are potentially unbounded in
size, it is generally both impractical and unnecessary
to process or query all the streaming data items. One
technique is to evaluate approximate queries not
over the entire past history of the data streams, but
rather only over certain temporal window which
only contains the most recent arrived data items. In
the spirit of the work in (B. Babcock et al., 2002)(D.
J. Abadi et al., 2003)(Zhu Y and Shasha D, 2002),
there are three kinds of popular window models:
landmark window model, sliding window model and
damped window model.
Although changing range of processing and
query to window model has already reduced the
resource requirements, it is impractical to processing
all the data items from data streams in some
scenarios. For example, many data stream sources
are prone to dramatic spikes in volume, and data
items arrive in a bursting fashion (bursting streams).
Peak load during a spike can be orders of magnitude
higher than typical load, and processing all the
arrived data items can still exceed system resource
availability. It becomes necessary to discard some
fraction of the unprocessed data items during a spike
(B. Babcock et al., 2002)(M. Datar, 2003)(A. Das et
al, 2003).
Here our discussion focuses on landmark
window over bursting streams, and the technique
that we propose for dropping some of the
unprocessed data items is random sampling.
1.2 Contributions and Organization
In this paper, we first discuss the classic reservoir
sampling algorithm and analyze its drawbacks when
it is directly used for landmark window over data
streams. Then, we propose a stratified multistage
sampling algorithm for landmark window, which
samples different data groups with unequal
probabilities and works even when the number of
data items in the landmark window varies
dramatically over time.
The organization of the rest of the paper is as
follows. Section 2 discusses related work. We
analyse the classic reservoir sampling algorithm in
section 3. SMS algorithm and the experimental
103
Longbo Z., Zhanhuai L., Min Y., Yong W. and Yun J. (2006).
RANDOM SAMPLING ALGORITHMS FOR LANDMARK WINDOWS OVER DATA STREAMS.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 103-107
DOI: 10.5220/0002440501030107
Copyright
c
SciTePress

results appear in section 4 and section 5. Finally,
section 6 concludes the paper.
2 RELATED WORK
Recently, there have been more and more interests in
data stream management system (DSMS) and its
related algorithms. A good overview can be found in
(B. Babcock et al., 2002) or (L. Golab and M.T.
Ozsu, 2003). A number of academic projects also
arise, such as STREAM(B. Babcock et al., 2002),
Telegraph(Sirish Chandrasekaran and Michael J.
Franklin, 2002), Aurora(D. J. Abadi et al., 2003),
StatStream(Zhu Y and Shasha D, 2002),
Gogascope(C. Cranor et al, 2002), etc. Landmark
window model is one of most popular window
model in data stream processing. Some data stream
algorithms over landmark window have been
presented (S. Guha et al., 2001)(Guha N. and
Koudas K, 2002).
Random sampling has been proposed and used in
many different contexts of DSMS. A number of
specific sampling algorithms have been designed for
computing quantiles (M. Greenwald and S. Khanna,
2001), heavy hitters (G. Manku and R. Motwani,
2002), distinct counts (P.Gibbons, 2001), adaptive
sampling for convex hulls (S. Guha et al., 2001) and
construction of synopsis structures (S. Guha et al.,
2001)(M Datar et al., 2002), etc. Many DSMSs
being developed support random sampling,
including the DROP operator of Aurora (D. J. Abadi
et al., 2003), the SMAPLE keyword in STREAM
(B. Babcock et al., 2002), and sampling functions in
Gigascope (C. Cranor et al, 2002). The classic
algorithm for maintaining an online random sample
is known as reservoir sampling (Vitter JS., 1985). It
makes one pass over data set and is suited for the
data stream model, but has some drawbacks to
directly used for sampling from landmark windows
over data streams.
3 THE CLASSIC RESERVOIR
SAMPLING
The reservoir sampling (Vitter JS., 1985) solves the
problem of maintaining an online random sample of
size k from a pool of N data items, where the value
of N may be unknown. It makes only one pass over
data set sequentially, and suits for data stream model
(B. Babcock et al., 2002)(S. Guha et al., 2001)(C
Jermaine et al., 2004). Let k be the number of data
items in sample R, n denote the number of data
items processed so far. The basic idea of reservoir
sampling can be described as follows (Vitter JS.,
1985)(T. Johnson et al, 2005):
Algorithm 1: The Classic Reservoir Sampling
Input: Data Stream S, k
Output: Sample R
1. Make first k data items
candidates for the sample R;
2. Process the rest of data items in
the following manner:
3. At each iteration generate an
independent random variable ζ (k,
n).
4. Skip over the next ζ data items.
5. Make the next data item a
candidate by replacing one at
random.
6. If the current number of
candidates exceeds k, randomly
choose a sample out of the
reservoir of candidates.
The classic reservoir sampling can be used for
data streams to select a random sample of size k. But
it has serious drawbacks to be directly used for
landmark window. First, reservoir sampling works
well when the incoming data contains only inserts
and updates but runs into difficulties if the data
contains deletions (S. Guha et al., 2001), it is
inefficient to delete data items in landmark window.
Second, when the number of data items in landmark
window exceeds the limited memory, a data item is
randomly selected to delete. Older data items and
newer ones are processed equally. A newer data item
may be deleted too early.
4 A STRATIFIED SAMPLING
ALGORITHM FOR
LANDMARK WINDOW
To overcome the drawbacks of reservoir sampling,
we use the basic window (BW) technique in
conjunction with reservoir sampling to present a
BW-based stratified multistage sampling algorithm
for landmark window (SMS Algorithm). Let T be
temporal span of the landmark window W, and the
time interval of W’s updating cycle is T
c
. We divide
the data items in W into k strata (or groups), and S[i]
denotes stratum i (i =1,2,…,k), the temporal span of
each stratum is equal to T
c
/m (m is a nonnegative
integer). f
0
denotes the sampling fraction in the
beginning, f
r
denotes re-sampling fraction.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
104
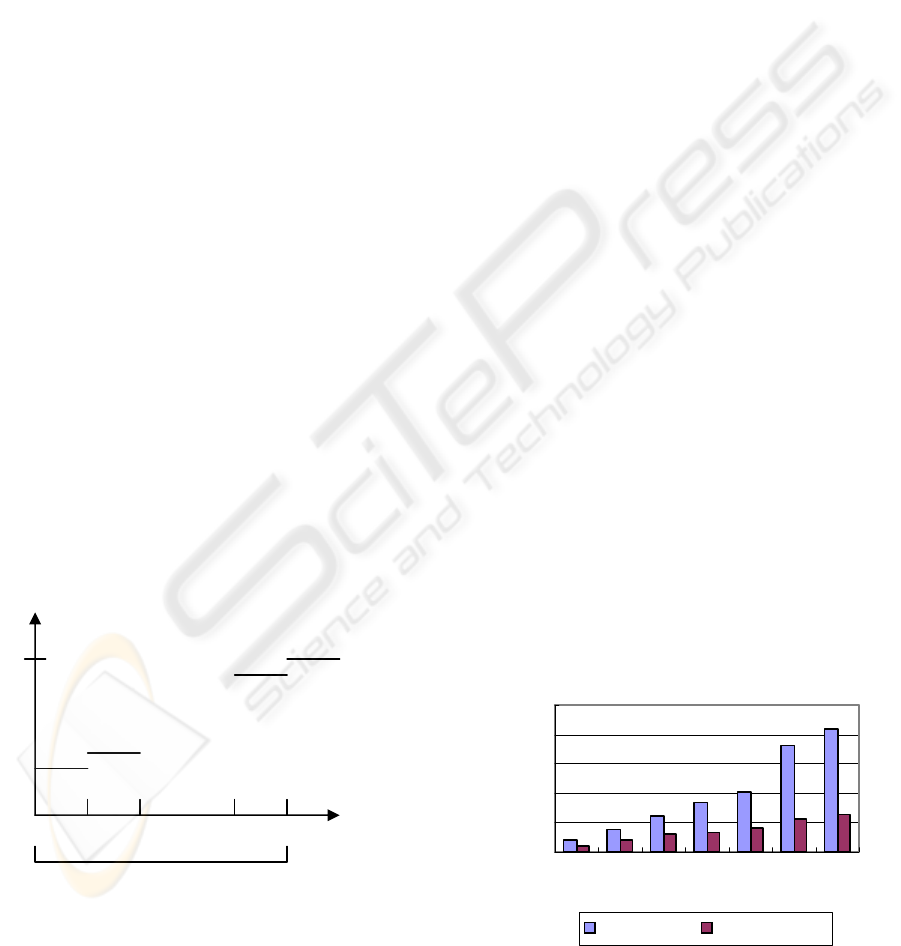
Data streams are temporally ordered, new items
are often more accurate or more relevant than older
ones. We will take a higher sampling fraction in the
newer strata than in the older strata by using
stratified multistage sampling (Shown in Fig. 1). The
following is the detailed steps of the SMS algorithm
(For simplicity, we suppose that the temporal span
of each stratum is equal to T
c
).
Algorithm 2: SMS algorithm
Input: Data Stream S, T, f
0
, f
r
Output: Landmark Window W
Initialize:
1. For each data item r from time
point 0 through T inclusive, add
it into landmark window W with
probability f0.
2. Divide W into k strata: S[0],
S(B. Babcock et al., 2002), …,
S[k-1].
Begin
3. Wait for a new data item r to
appear in data stream S, with
probability f0:
4. Add r into S[k];
5. If C then
6. Select a stratum S[i] (i∈
{0,1,.., k-1});
7. Re-sampling from S[i] using
reservoir sampling ; //The
sampling fraction is fr
8. End if
9. If it is time for W to move ahead
then
10. k = k +1;
11. End if
12. Skip to step 3;
End
In above description of SMS algorithm,
condition C is predefined, i.e. because peak load
during a spike can be orders of magnitude higher
than typical loads, then the available memory may
be insufficient to save all the data items in W and
S[k].
5 EXPERIMENTS EVALUATION
Data stream algorithms take as input data items
from data streams, where the data items are scanned
only once in the increasing order of the indexes (B.
Babcock et al., 2002)(L. Golab and M.T. Ozsu,
2003)(M. Datar, 2003). There are some key
parameters for data stream algorithms: (1) Storage:
the amount of memory used by the algorithms. (2)
Efficiency: the per-item processing time. (3)
Accuracy: guaranteeing accuracy of continuous
query results based on the summary structures.
Generally there are tradeoffs among these three costs
and no single, optimal solution. Here we compare
the storage, efficiency and accuracy of the classic
reservoir sampling algorithm (RS algorithm) and the
SMS algorithm in our experiments.
5.1 Comparison of Storage and
Efficiency
We ran reservoir sampling algorithm (RS algorithm)
and SMS algorithm on the dataset WorldCup98, the
access logs from the 1998 World Cup Web site. This
dataset consists of all the requests made to the 1998
World Cup Web site between April 30, 1998 and
July 26, 1998. During this period of time the site
received 1,352,804,107 requests. We choose
different landmark windows by choosing different
start time point. The experiments were performed on
a 2.4GHz Pentium 4 PC with 256MB main memory,
and the program is written in Borland C++ Builder
6. Fig. 2-3 shows the experimental results.
0
50
100
150
200
250
30 50 70 90 110 130 150
Time point
Time used (ms)
RS Algorit hm SM S A l go r it h m
Fi
g
ure 2: Com
p
arison of efficienc
y
.
S[0] S[1] … S[ k-1] S[k]
Temporal span T of current landmark window
Sampling fraction f
Figure 1: Different sampling fraction for different strata
at time T.
RANDOM SAMPLING ALGORITHMS FOR LANDMARK WINDOWS OVER DATA STREAMS
105

0
200
400
600
800
30 50 70 90 110 130 150
Time point
Memory used
RS Algorit hm SM S Algo r it h m
From the results of the experiment, we can see
that SMS algorithm achieves a significant
improvement on efficiency and uses the similar
memory comparing with the classic reservoir
sampling.
5.2 Comparing of Query Answer
Accuracy
Evaluating window aggregates on data streams is
practical and useful in many applications. Thus, we
compare SMS algorithm and the classic reservoir
sampling algorithm by comparing the accuracy of
evaluating window aggregates on the samples. The
experimental setup is similar to the one used in
section 4.1, and the same data sets are used.
0
1
2
3
4
5
30 50 70 90 110 130 150
Time point (min)
relative error (%)
RS Algorithm SMS Algorithm
We assume that the current temporal span of
landmark window is 150m, and the sampling
fraction of RS algorithm is equal to the average
sampling fraction of SMS algorithm. We ran SUM
function on the samples (it is easy to extend to other
aggregates), and the time rang of queries is recent
50m, 100m, 150m. Let f
0
=0.7, 0.8, 0.9, f
r
= 0.7, 0.8,
0.9 respectively and we finally calculate average
relative error. Fig. 4-6 shows the experimental
results.
0
1
2
3
4
5
30 50 70 90 110 130 150
Timepoint (min)
relative error (%)
RS Algorit hm SM S Algo r it h m
0
1
2
3
4
5
30 50 70 90 110 130 150
Timepoint (min)
relative error (%)
RS Algorit hm SM S Algo r it h m
As we observed above, the experiment shows
that the SMS algorithm is somewhat superior to RS
algorithm, especially when the time rang of queries
only contains the most recent data items.
6 CONCLUSIONS
Some typical algorithms, such as histogram, wavelet
representation, random sampling, sketching
techniques, clustering, and decision tree, can be used
for data streams model. Most of these algorithms
have been considered for traditional database. The
challenge is how to adapt some of these techniques
to the data stream model (B. Babcock et al., 2002)
(L. Golab and M.T. Ozsu, 2003). In this paper, we
present a sampling algorithm for processing data
items over landmark window. The algorithm
somewhat overcomes the drawbacks of the classic
reservoir sampling which can be directly used for
processing streaming data. The theoretic analysis
Fi
g
ure 3: Com
p
arison of stora
g
e.
Figure 4: Comparing accuracy of query answer (the
rang of time is recent 50m).
Figure 5: Comparing accuracy of query answer (the
rang of time is recent 100m).
Figure 6: paring accuracy of query answer (the rang of
time is recent 150m)
.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
106

and experiments show that the algorithm is effective
and efficient for continuous data streams processing.
ACKNOWLEDGMENTS
This work is supported by the National NSF of
China under grant No. 60373108 and in part by the
National Research Foundation for the Doctoral
Program of Higher Education of China under grant
No. 2069901.
REFERENCES
B. Babcock, S. Babu, M. Datar, R. Motwani, and J.
Widom. Models and issues in data stream systems.
Proceedings of 21st ACM SIGACT-
SIGMODSIGART Symp. on Principles of Database
Systems, pages 1–16, Madison,Wisconsin, May 2002.
L. Golab and M.T. Ozsu. Issues in data stream
management. SIGMOD Record, Vol. 32, No. 2, 2003.
Sirish Chandrasekaran and Michael J. Franklin. Streaming
queries over streaming data. Proceedings of the 28th
VLDB Conference, Hong Kong, China, 2002.
D. J. Abadi, D. Carney, U. Cetintemel, et al. Aurora: a
new model and architecture for data stream
management. The VLDB Journal (2003) /Digital
Object Identifier (DOI) 10.1007/s00778-003-0095-z
Zhu Y, Shasha D. StatStream: Statistical monitoring of
thousands of data streams in real time. Proceedings of
the 28th Int’l VLDB Conference. Hong Kong, China,
2002. 358~369.
Vitter JS. Random sampling with a reservoir. ACM Trans.
on Mathematical Software, 1985, 11(1): 37-57.
Gibbons PB, Matias Y. New sampling- based summary
statistics for improving approximate query answers.
Proceedings of the 1998 ACM SIGMOD International
Conference on Management of Data. Seattle,
Washington, United States. 1998.331 – 342.
S. Guha, N. Koudas, K. Shim. Data Streams and
Histograms. Symposiumon the Theory of Computing
(STOC), July 2001.
M Datar, A Gionis, P Indyk, et al. Maintaining stream
statistics over sliding windows. The 13
th
Annual
ACM-SIAM Symp on Discrete Algorithms, San
Francisco, California, 2002.
C Jermaine, A Pol, S Arumugam. Online Maintenance of
very large random samples. SIGMOD 2004, June 13-
18, 2004, Paris, France.
M. Datar. Algorithms for data stream systems. PhD thesis.
2003
A. Das, J. Gehrke, M. Riedwald. Approximate join
processing over data streams. SIGMOD 2003, June 9-
12, 2003, San Diego,CA
T. Johnson, S. Muthukrishnan, I. Rozenbaum. Sampling
Algorithms in a Stream Operator. SIGMOD Record
2005.
C. Cranor, T. Johnson, O. Spatschnek, V. Shkapenyuk.
Gogascope: A Stream Database for Network
Applications. SIGMOD 2002, page 262, 2002.
http://ita.ee.lbl.gov/html/contrib/WorldCup.html
S. L. Lohr. Sampling: design and analysis. Duxbury Press,
a division of Thomson Learning.
M. Greenwald and S. Khanna, Space-efficient online
computation of quantile summaries, SIGMOD 2001.
G. Manku and R. Motwani. Approximate frequency
counts over data streams. Proceedings of VLDB, Hong
Kong, China, 2002. 346-357.
S. Guha, N. Koudas, K. Approximating a Data Stream for
Querying and Estimation: Algorithm Performance
Evaluation. Proceedings of the 18th International
Conference on Data Engineering (ICDE.02). San Jose,
California, USA, 2002.
P.Gibbons. Distinct sampling for highly-accurate answers
to distinct values queries and event reports.
Proceedings of the 27
th
VLDB conference, Roma,
2001. 541-550.
RANDOM SAMPLING ALGORITHMS FOR LANDMARK WINDOWS OVER DATA STREAMS
107
