A VIEWPOINTS MODELING FRAMEWORK BASED ON

EPISTEMIC LOGIC

Min Jiang

Computer School of Wuhan University, City University of HongKong Shenzhen Research Institute,Shenzhen Virtual

University Park, Shenzhen Hi-tech Industrial Park, Shenzhen, 518057,China

Guoqing Wu

Computer School of Wuhan University, Luojia Hill, Wuhan, 430072, china

Keywords: Viewpoints, overlapping requirement, common knowledge, inconsistency, epistemic logic.

Abstract: The approach of viewpoints-oriented requirement engineering hopes that stakeholders in a complex system

should describe it from their own perspectives and then generate a more complete requirement specification.

Just because of this characteristic, several stakeholders may describe a same problem. These overlapping

requirements are the source of inconsistency. This paper puts forward a requirements modeling framework

based on problem-domain and viewpoints. We interpret and reason it with epistemic logic in order to make

requirements more structured and help stakeholders formally discover those inconsistent overlapping

requirements.

1 INTRODUCTION

The approach of viewpoints-oriented requirement

engineering intends to capture the stakeholders’

requirements in a more comprehensive way. All the

people related to the target system describe the

system’s properties independently in their familiar

way according to their responsibilities, experience

and skills. Just because of this characteristic, it

unavoidably leads to the tangled and scattered

requirements. If stakeholders have different

understanding of those requirements, inconsistency

will emerge. So the essential problem of the

viewpoints method is to ensure that the present is of

consistency or coherence.

Recently, many researchers propose kinds of

methods to solve inconsistency of viewpoints-based

requirements specification. Typical work on this

topic is that by A. Finkelstein et al. for action-based

temporal logic; Zave & Jackson propose the

composition of partial specifications as a

conjunction of their assertions in a form of classical

logic. S. Easterbrook and M. Chechik use an

underlying multi-valued logic to describe each

viewpoint, propose the framework for merging and

reasoning about multiple, inconsistent state machine

models, and implement the multi-valued logic

checker. M. Sabetzadeh and S. Easterbrook propose

a category-theoretic approach to representation and

analysis of inconsistency in graph-based viewpoints.

However, what requirement specification reflects

are stakeholders’ knowledge, belief and intention,

which are all related to epistemic properties. When

participants have different understandings or

interpretations about those properties among them,

inconsistency and incompleteness will occur.

Therefore, it is necessary to solve the inconsistency

from epistemic perspective. But the existing

approaches are insufficient.

After studying these approaches, we propose

Problem-Domain-based Viewpoints Modeling

Framework (PDVMF) and use epistemic logic to

interpret it. Through reasoning those epistemic logic

formulas we can transform the problem of

discovering absolute inconsistency into solving SAT

problem, and common knowledge can be used to

help stakeholders deal with relative inconsistency.

2 PROBLEM-DOMAIN-BASED

VIEWPOINTS MODELING

FRAMEWORK

In the real world different people play different roles

in large-scale software development and they

consider problems from different levels. They are

grouped into different teams. Member of a team

interact each other and form the team’s specification,

meanwhile, different teams influence mutually and

435

Jiang M. and Wu G. (2006).

A VIEWPOINTS MODELING FRAMEWORK BASED ON EPISTEMIC LOGIC.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - ISAS, pages 435-439

DOI: 10.5220/0002444104350439

 SciTePress

present final one. Whether the requirements of every

stakeholder are reasonable depends not only on

himself but on which team he belongs to when he

proposes the requirements and other team members’

requirements.

In view of the above problems, the viewpoints

model we are going to propose should reflect the

following aspects:

1) Viewpoints model should be 2-dimension, i.e.

software system should consist of some problem

domains. A team in the real world corresponds to a

problem domain. And one problem domain has

some viewpoints, which means that it needs

different kinds of people’s cooperation to solve one

problem.

2) The relationship among goals, FRs and NFRs

must be explicitly expressed and treated as a whole

so as to make stakeholders’ requirements more

structured.

Viewpoint represents stakeholders’ requirements

for the target system in specification. Whether the

target system satisfies stakeholders’ requirements

during capturing requirements depends upon

whether goals are achieved. The achievement of

goals is supported by FRs and these two are linked

by NFRs. When FRs and NFRs related to a certain

goal are fulfilled, the goal is considered to be

achieved, i.e.

RNFR

Goal . Through tracing a

goal, we can reason out the related FRs and NFRs,

that is,

Goal

,FR NFR . Figure 1 shows the

relationship among the three kinds of entities.

NFR

Figure 1: Requirement block with refine relationship.

We call the combination of the three entities a

requirement block, considered as the core of

PDVMF. Based on the former viewpoints’

researches (B. Nuseibeh et al., 1994), PDVMF

collects and expresses stakeholders’ requirements

using templates.

Problem domains are divided by domain experts

and system analysts. Then after affirming the

relationship among sub-problem domains, that are

involved and the cooperative relationship among

those participants, stakeholders can describe their

requirements using a viewpoints template, according

to the sub-problem domain which they are

concerned with. In general, problem domain level is

concerned with the global and abstract description,

while viewpoint level is related to the partial and

concrete one. Figure 2 shows the overview of

PDVMF.

Figure 2: Viewpoints modeling framework based on

problem domains.

3 REASONING ABOUT

INCONSISTENCY IN PDVMF

“Knowing” is an important research object in

epistemic logic, which formalizes the meaning of

“knowing”. In the real world, the cognitive subject is

not a single person, or human beings with unified

cognition, but a group of individuals with different

knowledge. Halpern and Moses[6] analyze epistemic

logic and indicate that Kripke’s possible world

model is an effective tool to study.

Let

be a set of atomic propositions. A kripke

structure M over

is a m+2 tuple

M,R,R...,R,

<> , where W is a finite set

of possible worlds,

is a function that labels each

possible world with the set of atomic propositions

true in that possible world. For every i,

R is a

binary relation over

W , which means that if

is true, in the view of Agent i in the possible world

, the possible world

is an accessible realistic

world.

K is a modal operator. The formula

is read

“agent

a knows

”, which means that

is true in

all accessible possible worlds of

a . On the contrary,

is false at least in one accessible possible world,

“agent

a doesn’t know

”, represented by

¬ . If

is false in all accessible possible

worlds, “agent

a knows

¬ ”, represented by

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

436

From the technical perspective, we adopt the

system named

S [6]. The system having m agents

consists of the following axioms and rules:

(A1) All proposition tautologies

(A2)

(K K ( )) K

ii i

ϕφ φ

∧→→,

1, ...im=

(A3)

→ ,

1, ...im=

(A4)

KKK

iii

→ (Positive introspection)

(A5)

KKK

iii

¬→¬(Negative introspection)

(R1)

ϕφ

→

(R2)

( 1... )

We briefly explain epistemic logic using an

example. Let

be a Kripke structure

{, , ,}

Alice Bob

MWR R

= , where W ={

123

ss},

={Alice, Bob} is a set of agents, Φ ＝｛

｝,

Alice

R (real line) and

(dashed) are an

accessible relation.

is shown in Figure 3.

Figure: 3: Kripke structure

Let

= “finish transaction within one second”,

so we can infer:

(1)

(M, )

(2)

(M, )

Alice Bob Bob

K(K K )pp∨¬{Alice

knows Bob knows whether

is hold in

, because

Bob

is hold in

and

Bob

¬ is hold in

}

3.1 PDVMF and Epistemic Logic

PDVMF is viewed as a double-layer structure: every

sub-problem domain or every viewpoint is regarded

as a possible world. The requirements presented by

stakeholders are sets of epistemic logic propositions.

Whether it is true or not lies on the truth value of the

accessible possible world.

Viewpoints level is represented by 3 tuple

pd v v

MVD

=< ℜ >

, where

{}

, ,...,

iiii

pd pd pd pd

VD vd vd vd= is

every viewpoint in sub-problem domain

pd ,

{

}

:(P ,)

VD true false

→→ stands the labelling

function of atomic propositions in every viewpoint,

and

VD VDℜ⊆ is called the accessibility relation

and means the dependency relation between every

pair of participants in the same problem domain.

Over this structure we define two modal operators:

(“viewpoint i knows

”) and, M

which

is equal to

¬ (“viewpoint i does not know if

is true or not”). In order to reason over our model

conveniently, we add some rules intuitively.

(R3)

Goal

...

Sub Goal Sub Goal Sub Goal

∧

∧∧ , if it is the

AND relation between goals and sub-goals;

(R4)

Goal

...

Sub Goal Sub Goal Sub Goal∨∨∨, if it is the

OR relation between goals and sub-goals;

(R5)

Goal

(.. ..)(..)( .. ..)

ij p qpq

xx x xx x

un Fun NF NF Fun Fun NF NF∧∧∧∧∨∨ ∧∧∧ ∧

, indicating that a certain goal can infer the related

FRs and NFR;

Thus the requirement block in viewpoint

template can be translated to epistemic logic

formulas.

In the same way, problem domain level is also a

Kripke structure

<,,

S= PD

ℜ>

{

}

, ,...,

PD pd pd pd= is a set of sub-problem

domains;

{

}

:(P ,)

PD true false

→→ is the labelling

function of rational propositions viewed as by all

stakeholders in a certain problem domain.

PD PD

ℜ

⊆× refers to the dependency

relation between sub-problem domains.

We can translate the requirements verified on the

viewpoints level into the epistemic logic

propositions again, and then reason them on the

upper problem domain level to discover

inconsistency among those requirements and finally

form the final requirements specification.

3.2 Common Knowledge in PDVMF

Common knowledge refers to some facts several

stakeholders know. Overlapping requirements are

common knowledge existing among stakeholders.

When stakeholders have different understanding

about these requirements, inconsistency will occur.

For the sake of reasoning about common

knowledge, we introduce two operators:

and

. E

is read “every viewpoint knows

A VIEWPOINTS MODELING FRAMEWORK BASED ON EPISTEMIC LOGIC

437

in the problem domain

pd ” and CK

is read

“

is a common knowledge in the problem domain

pd ”. They can be represented as follows:

EKK..K

iii i

pd pd pd pd

VD VD VD

ϕϕ ϕ

=∧∧∧

CK EEE..(E)

iiii i

pd pd pd pd pd

ϕϕ ϕ ϕ

=∧ ∧ ∧∧

To explain the semantic of two operators, suppose

,,MS

=< ℜ > is a viewpoint level model, and let

tS∈ .

⎯

⎯→ represents that

can access

within one step through

R ；

t→ represents (,)st ∈ℜ;

⎯

⎯→ represents the reflexive transitive

closure of one-step-accessibility relation.

The semantics of two both operators is:

(M, )

⇔ for every

satisfying

t→

(M, )t

is hold;

(M, )

⇔ for every t satisfying

⎯

⎯→ , (M, )t

is hold.

Through the two newly introduced operators, we

can reason about stakeholders’ requirements

expressed by epistemic logic formulas and judge if

the requirements are known by all stakeholders or if

they are common knowledge.

3.3 Identifying Inconsistency

In the requirement modeling process, inconsistency

can be divided into two types:

1) Absolute inconsistency. E.g. viewpoint A

thinks “log” is necessary, while the related

viewpoint B unnecessary.

2) Relative inconsistency E.g. viewpoint A

thinks “log is necessary and it must finished within

one second”, while viewpoint B “log is necessary,

but it need not be finished within one second”.

Absolute inconsistency can be found through

checking whether the formula

p¬∧¬¬

is satisfiable or not. The formula means that

“viewpoint

i knows

is false in some related

viewpoints and true in some other viewpoints”. If

the formula is true, then absolute inconsistency

exists. For instance, in the Kripke structure shown in

Fig. 3, we can infer:

(M, )

Alice Alice

KKpp¬∧¬¬, because in

the possible worlds

s , Alice knows p is true,

but in the possible world of

s the conclusion is the

opposite. So Alice can infer that

s and

have inconsistent views of

. In this way, we can

transform the problem of discovering absolute

inconsistency into solving a SAT problem.

Due to its speciality, relative inconsistency is

difficult to discover relative inconsistency in the way

of complete formalization. The approach we find

and solve relative inconsistency is to find out all

common knowledge using operator

CK . Part of it

may be relatively inconsistent, so all stakeholders

need to discuss all common knowledge together to

see whether they have different understandings

about it. This method can help stakeholders to

discuss possible inconsistent requirements in a

confined scope.

4 A SIMPLE EXAMPLE

We take an example of a simplified online-library

system to explain our approach. For simplicity, we

only study the stakeholders in a certain problem

domain and simplify their requirements. Suppose

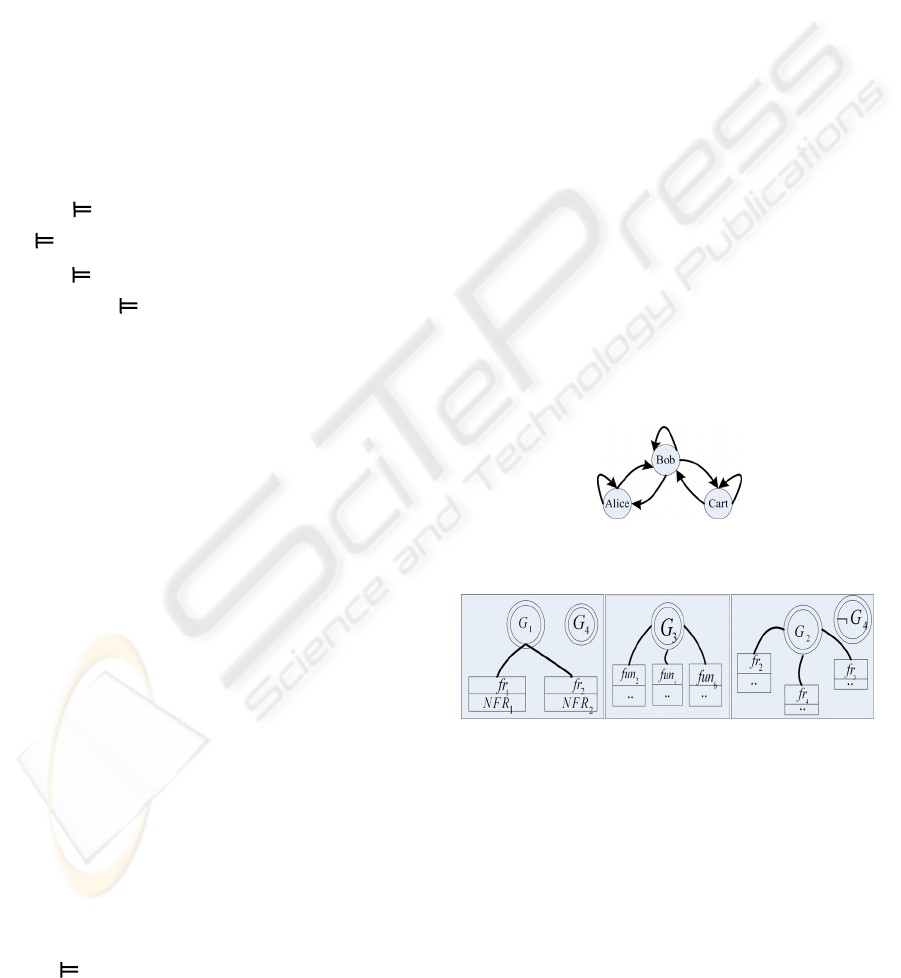
reader Alice, librarian Bob, and supplier Cart are

involved in problem domain D. The relationship

between them is shown in Fig. 4

Figure 4: Relationship between the stakeholders in

problem domain D.

Figure 5: Alice’s requirement block; Figure 6: Cart’s

requirement block; Figure 7: Bob’s requirement block.

Alice’s requirement block expressed in natural

language is: if to achieve goal

G ,

r and

constrained respectively by

nfr and

nfr , must be

satisfied, where

G denotes “book borrow”;

“search catalogue and delivery books”;

r “log”;

nfr “finish within one minute”;

nfr “ensure

operation’s reliability”. They are all epistemic logic

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

438

propositions. Similarly,

G is “readers’

information’s management”;

G is “catalogue’s

management”;

G is “all the books can be

borrowed”;

r is “query readers’ information”;

is “modify or delete readers’ information”;

r is

“add new catalogue”;

r is “modify the present

catalogue”.

So we have:

(, )

Bob

G¬

(, )

Bob

G¬

(, )

Alice

(, )

Bob

G¬¬ (According to the

relation with Bob)

(, )

Bob

Bob Bob

GG¬∧¬¬

Namely, in the view of Bob,

G is an absolutely

inconsistent requirement, which require further

negotiation between Bob and other stakeholders.

(, )

Alice

(, )

Alice

G (Completeness)

rnfr∧ (R5)

(, )

Alice

in the same way

(, )

Bob

(, )

Alice

r and

(, )

Alice

Bob

Then we can infer

(, )

Alice

Alice Bob

rfr∧

i.e. if Alice and Bob know

r , then

r may be

relatively inconsistent whose existence depends on

their discussion. If they discover relative

inconsistency after discussion, then they can take

methods to solve it.

Likewise, we find

r is a common knowledge

with operator

CK , so Cart must join discussion.

5 CONCLUSION

The rationality of the requirement presented by a

stakeholder is related to its domain as well as

whether other stakeholders in the same domain agree

with him. Stakeholders’ different interpretations

about overlapping requirements will induce

inconsistency. However, the existing methods of

handling inconsistency are rarely concerned with

these epistemic attributes. So we hope to find and

solve inconsistency from the epistemic perspective

through proposing PDVMF and interpreting it with

epistemic logic.

Our approaches can not express the characteristic

of knowledge that it has timeliness. For example, in

the same problem domain D, agent i knows

time

t , but he knows

at time

. If we can’t

overcome this weakness, to handle the changing

requirements and trace the requirements is

impossible.

In addition, just like temporal logic, epistemic

logic is a variety of modal logic. There are lots of

model checkers based on temporal logic. Now we

are implementing a model checker for PDVMF

through adapting SMV which is a well-known

model checker based on temporal logic.

REFERENCES

Finkelstein, A., Gabbay, D., Hunter, A., Kramer, J.,

Nuseibeh, B. (1994), Inconsistency handling in

multiperspective specifications. IEEE Trans. on

Software Engineering,20(8):569-578.

Zave, P., and Jackson, M. (1993) Conjunction as

Composition; Transactions on Software Engineering

and Methodology, 2(4), 379-411.

Easterbrook, S., and Chechik, M. (2001), A Framework

for Multi-Valued Reasoning over Inconsistent

Viewpoints. In Proceedings of the 23rd International

Conference on Software Engineering(ICSE’01)

(Toronto, Ontario, Canada May 12-19, 2001), IEEE

Computer Society, 411 - 420

Sabetzadeh, M., & Easterbrook, S. M. (2003), Analysis of

Inconsistency in Graph-Based Viewpoints: A

Category-Theoretic Approach. In Proceedings of the

18th IEEE Int. Conf. on Automated Software

Engineering(ASE 2003) (Montreal, Canda, Oct. 6-10,

2003), IEEE Computer Society, 12-21

Nuseibeh B, Kramer J, Hunter A. (1994), A framework

for expressing the relationships between multiple

views in requirements specification. IEEE Trans. on

Software Engineering, 1994,20(10):760-773.

Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. Y.

(1995), Reasoning About Knowledge. The MIT Press:

Cambridge, MA.

A VIEWPOINTS MODELING FRAMEWORK BASED ON EPISTEMIC LOGIC

439