
A GUI FOR DATA MART SCHEMA ALTERATION
Nouha Bouaziz, Faiez Gar
g
ouri
Institut Supérieur d’Informatique et du Multimédia de Sfax, Sfax, Tunisie
Jamel Feki
Faculté des Sciences Economiques et de Gestion de Sfax, Sfax, Tunisie
Keywords: Data mart, Multidimensional schema, XML, Visualization, Schema alteration.
Abstract: This paper is interested in the graphical manipulation of data mart schemes described in XML and issued
from a generation module of multidimensional models. This manipulation is performed through a set of
operations we have defined. These operations consist in adding, deleting and renaming the multidimensional
elements.
1 INTRODUCTION
A Data Warehouse (DW) is a special data base
storing a huge volume of data dedicated to
decisional systems. Its design methodology must
take in account several things, among them the
heterogeneity of data sources, the correspondence
between data source models and multidimensional
models as well as the manipulation of data
structures. In a DW context, the data structure
manipulation becomes really a crucial subject of
research; especially in the design phase of DWs or
Data Marts (DM) (Kimball, 1996) (Tryfona and al,
1999) (Moody and al, 2000) (Bonifati and al, 2001).
DMs are extracted from the DW; they are
characterized by their multidimensional schemes
(MDS). These MDS are represented as diagrams
generally in respect to the Golfarelli formalism
(Golfarelli and al, 1998).
Our team researches are in the context of
designing a semi-automatic DW hybrid
methodology summarized by the following steps:
i) acquisition of the OLAP requirements
expressed as tabular sheets (Feki, 2004),
ii) derivation of the DM schema on the basis of the
OLAP requirements (Soussi and al, 2005),
iii) generation of the DW schema by integrating
DM schemes (Majdoubi and al, 2005).
Our contribution in this paper consists in the
visualization and the graphical manipulation of DM
schemes. Actually, these schemes are described in
XML and resulted from a generation module (i.e.,
step ii above). More accurately, it is to develop a
GUI assuring two main tasks: i) the visualization of
the DM schema and ii) the alteration of the DM
schema.
This paper is organized as follows: section 2
gives an overview of our context of study. Section3
defines the multidimensional basic concepts. Section
4 defines our alteration operations: addition,
deletion, and rename of multidimensional elements.
Section 5 deals with the prototype of the interface
whereas section 6 summarizes the presented work
and introduces its perspectives.
2 CONTEXT OF STUDY
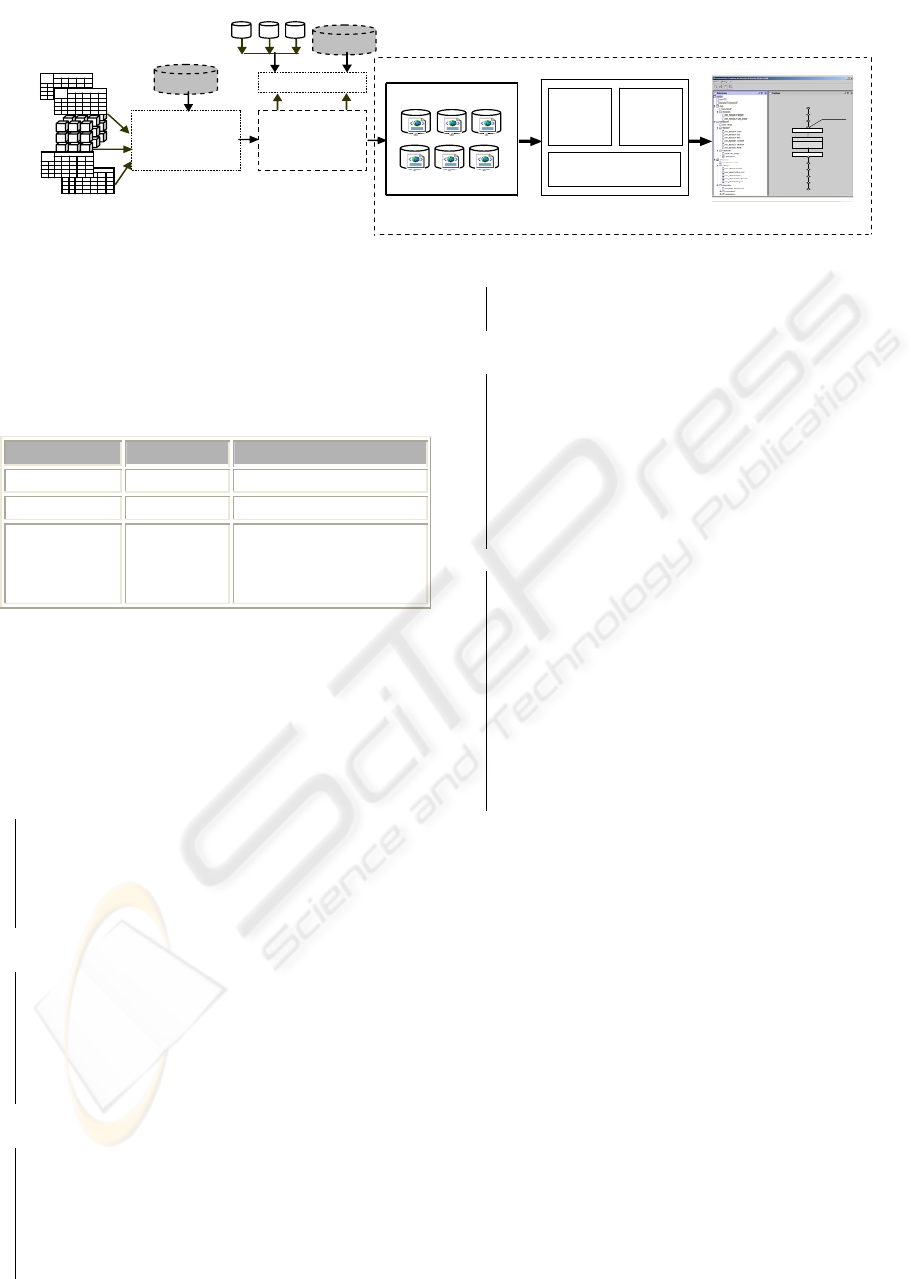
The work presented in this paper is a part of an
ongoing project. Figure 1 illustrates its general
context where the dashed box borders the scope of
this study i.e., the visualization and the alteration of
the DM schema.
The visualization accepts star/constellation
schemes described in XML. It displays the DM
schema either as a tree or as a multidimensional
diagram that highlights the multidimensional
concepts (fact, dimensions, hierarchies, etc.). Since
the Golfarelli formalism (Golfarelli and al, 1998) is
the almost popular in drawing multidimensional
schemes, we adopt it to visualize DM schemes.
169
Bouaziz N., Gargouri F. and Feki J. (2006).
A GUI FOR DATA MART SCHEMA ALTERATION.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 169-174
DOI: 10.5220/0002449701690174
Copyright
c
SciTePress
MDS
Generation
Module
DM schema
described in XML
OLAP
Requirements
OLAP
Requirements
Graphical
Acquisition
Ontology
Ma
pp
in
g
Data sources
GUI
PURCHASE
Amount
Qtity_purch
TIME
Month
Day
IdT
Quarter
Semester
Year
SUPPLIER
City
Department
Region
IdS
Social_Name
MDS GUI
MDS
Explorer
Module
MDS
Diagram
Module
MDS Alteration
Module
Ontology
Star schema
Constellation
schema
Figure 1: GUI architecture for MDS handling.
The alteration consists in modifying these
schemes through suitable operations listed in Table1.
This manipulation aims to adapt and refine the
generated MDS in respect to the user requirements.
Table 1: Categories of operations on a MDS.
Operations Inputs Outputs
Display Tree XML Script
MDS Tree
Display MDS
Tree
MDS diagram
Alter MDS
Addition,
Deletion,
Rename.
MDS MDS diagram altered
3 BASIC CONCEPTS
To clarify our operations for MDS alteration, we
find necessary to define the multidimensional
concepts as presented in (Nabli and al, 2005).
- Fact definition
A fact F is defined as (Name
F
, M
F
) where:
- Name
F
is the name of the fact which represents
the analysis subject,
- M
F
= {M
F
1
, M
F
2
,…, MF
N
}; is the set of all
measures of F.
- Measure definition
A measure M
F
i
, of a fact F, is defined by the
couple (NameM
F
i
, FuncM
F
i
) where:
- NameM
F
i
, is the name of the measure,
- FuncM
F
i
, is the compatible aggregation function
with every measure, with FuncM
F
i
⊆ {Min, Max,
Sum, Average, Count}.
- Dimension definition
A dimension D, representing an analysis
perspective, is defined by the triplet (Name
D
, A
D
,
H
D
) where:
- Name
D
is the name of the dimension,
- A
D
= {A
D
1
, A
D
2
,…, A
D
N
}; is the set of all
attributes composing a dimension D,
- H
D
= {H
D
1
, H
D
2
,…, H
D
N
}; is the set of all
hierarchies associated with the dimension D.
- Hierarchy definition
A hierarchy is an acyclic graph defined by the
couple (Name
H
, P
H
) where:
- Name
H
is the name of the hierarchy,
- P
H
= <p
1
, p
2
,…, p
N
> ; is an organization of the
strong attributes of the hierarchy H
D
i
of D such as
p
i
Æ
p
j
means that the parameter p
i
has a
granularity strictly finer than p
j.
- Multidimensional schema
A multidimensional schema S is constituted of
measured facts associated to analysis dimensions.
It is defined by (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
)
where:
- Name
S
is the name of multidimensional schema,
- Dom
S
is the name of analysis domain of S,
- F
S
= {F
1
, F
2
,…, F
N
}; is the set of all facts of S,
- D
S
= {D
1
, D
2
,…,D
N
}; is the set of all dimensions
of S,
- Func
S
is a function that associates to every fact
F
i
a set D
S
of dimensions.
4 SCHEMA ALTERATION
This section defines a set of operations useful to
alter a DM schema (star or constellation). These
operations are the addition, the deletion, and the
rename of multidimensional elements. They are
those defined in (Nabli and al, 2005), and extended
with display and rename operations. We present
them in the following sub-sections.
4.1 Addition Operations
The addition operations insert new multidimensional
elements into a MDS. We define five operations
depending on whether we add a hierarchy, a
measure, a dimension, an attribute or a fact.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
170
- Hierarchy addition
The hierarchy addition inserts a new hierarchy into
an existing dimension of a MDS.
Definition
The hierarchy addition operation AddH adds a
hierarchy to a dimension. Its syntax is:
AddH (S, D, H) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- D = (Name
D
, A
D
, H
D
) is a dimension of S,
- H
=
(Name
H
, P
H
) is the hierarchy to be added to
D, where H.P
H
= <p
1
, p
2
,…, p
N
>.
Conditions:
- D∈ S.D
S
and H
∉ D.H
D
Outputs:
S’ is the MDS S enriched by the hierarchy H
where:
- S’ = (Name
S
, Dom
S
, F
S
, D
S
’,
Func
S
),
- D
S
’ = {D
1
, D
2
, …, D’, …, D
N
} ;
D’ = (Name
D
, A
D
’, H
D
’),
- A
D
’
= A
D
∪ {p
1
} ∪ {p
2
} ∪… ∪ {p
N
};
- H
D
’ = H
D
∪ {H}
.
- Measure addition
The operation adds a measure to a fact.
Definition
The measure addition operation AddM inserts a
new measure into a fact in a MDS. Its syntax is:
AddM (S, F, M) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is a fact of S where M
F
=
{M
F
1
,
M
F
2
,…, M
F
N
} is the set of all measures
constituting F,
- M
=
(NameM
F
i
, FuncM
F
i
) is the measure to be
inserted into F.
Conditions:
- F∈ S. F
S
and M
∉ F.M
F
Outputs:
S’ is the MDS S whose F fact is enriched by the
measure M where:
- S’ = (Name
S
, Dom
S
, F
S
’, D
S
,
Func
S
),
- F
S
’= {F
1
, F
2
, …, F’,…, F
N
}; F’
= (Name
F
, M
F
’),
- M
F
’
= M
F
∪ {M}.
- Dimension addition
This operation inserts a new dimension into a MDS
and preserves its nature (star or constellation).
Definition
The dimension addition operation AddD adds a
dimension to a set of facts in a MDS. Its syntax is:
AddD (S, F, D) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is the fact to which a new
dimension will be associated,
- D
=
(Name
D
, A
D
,
H
D
) is the dimension to be
added to F.
Conditions:
- F ∈ S.F
S
; D∉ S.D
S
; A
D
∉D
S
.A
D
and
H
D
∉ D
S
.H
D
Outputs:
S’ is the MDS enriched by the dimension D
where:
- S’ = (Name
S
, Dom
S
, F
S
, D
S
’,
Func
S
’),
- D
S
’ = D
S
∪ D,
- ∀ f ∈ F
S
; Func
S
’ (f) =
Func
S
(f)
∪ D.
- Attribute addition
The attribute addition operation inserts a parameter
into a hierarchy of a
dimension.
Definition
The attribute addition operation AddA inserts a
new attribute into a hierarchy of a dimension. Its
syntax is:
AddA (S, D, H, L,
A) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- D
=
(Name
D
, A
D
,
H
D
) is a dimension,
- H
D
=
(Name
H
, P
H
) is a hierarchy of D where A
will be added,
- L: is the insertion level of A
in H,
- A: is the attribute to be added.
Conditions:
- D ∈ S.D
S
; H
∈ D.H
D
;
A
∉ D.A
D
and L > 1
Outputs:
S’ is a MDS whose one of its dimensions is
enriched by a new attribute A
.
- S’ = (Name
S
, Dom
S
, F
S
, D
S
’,
Func
S
),
- D
S
’ = {D
1
, D
2
, …, D’, …, D
N
};
D’ = (Name
D
, A
D
’, H
D
’),
- A
D
’= A
D
∪ {A}; H
D
’= (Name
H
, P
H
’
.
) ;
P
H
’ = <p
1
, …, p
L-1
, A, p
L+1
,…, p
N
>.
- Fact addition
The addition of a fact F to a star schema having
common dimension(s) with F transforms the star
into constellation.
Definition
The fact addition operation AddF inserts a new
fact into a MDS. Its syntax is:
AddF(S, F, Dim) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is the fact to be inserted into S,
- Dim
=
{d
F
1
, d
F
2
,…, d
F
N
} is a set of dimensions
to which F can be associated.
Conditions:
- F∉ S. F
S
; Dim ⊆ S.D
S
and
Dim ≠ ∅
Outputs:
S’ is the MDS S enriched by F where:
- S’ = (Name
S
, Dom
S
, F
S
’, D
S
,
Func
S
’),
A GUI FOR DATA MART SCHEMA ALTERATION
171
- F
S
’ = F
S
∪ F,
- ∀ d ∈ Dim
; Func
-1’
(d) =
Func
-1
(d) ∪ F.
4.2 Deletion Operations
This category of operations deletes multidimensional
elements without correspondent in the data source.
We distinguish the deletion of a hierarchy, a
measure, a dimension, an attribute or a fact.
- Hierarchy deletion
This operation deletes a hierarchy of a dimension
from a MDS and maintains the schema nature.
Definition
The hierarchy deletion operation DelH deletes a
hierarchy from a dimension. Its syntax is:
DelH (S, D, H) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- D = (Name
D
, A
D
, H
D
) is a dimension of S,
- H
=
(Name
H
, P
H
) is the hierarchy to be deleted to
S, with H.P
H
= <p
1
, p
2
, ..., p
N
>.
Conditions:
- D ∈ S.D
S
;
H
∈ D.H
D
; | H
D
| >= 2 and
- A
D
= A
D
∪{p
1
} ∪ {p
2
} ∪… ∪ {ps};
∀ a ∈ A
D
, ∀ H
∈ D.H
D
a ∉ H.P
H
Outputs:
S’ is the MDS S not having the hierarchy H
where:
- S’ = (Name
S
, Dom
S
, F
S
, D
S
’,
Func
S
),
- D
S
’ = {D
1
, D
2
, …, D’, …, D
N
};
D’ = (Name
D
, A
D
’, H
D
’),
- A
D
’ = A
D
\ {p
i
∈ H.P
H
, H.p
i
∉ (H
D
- H)}
- H
D
’ = H
D
\ {H}
.
- Measure deletion
Measure to be deleted must not be the single one in
its fact.
Definition
The measure deletion operation DelM deletes a
measure from a fact. Its syntax is:
DelM (S, F, M) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is a fact of S where M
F
=
{M
F
1
,
M
F
2
,…, M
F
N
} is the set of all measures belonging
to F,
- M
=
(NameM
F
, FuncM
F
) is the measure to be
deleted.
Conditions:
- F∈ S. F
S
;
M
∈ F.M
F
and | M
F
| >= 2
Outputs:
S’ is a MDS where the measure M is removed
from the fact F where:
- S’ = (Name
S
, Dom
S
, F
S
’, D
S
,
Func
S
),
- F
S
’= {F
1
, F
2
, …, F’,…, F
N
}; F’
= (Name
F
, M
F
’),
- M
F
’
= M
F
\ {M}.
- Dimension deletion
A dimension could be deleted if and only if it is not
the single one in its MDS.
Definition
The dimension deletion operation DelD deletes a
dimension from a fact in a MDS. Its syntax is:
DelD (S, F, D) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is a fact from which a
dimension D will be removed,
- D
=
(Name
D
, A
D
,
H
D
) is the dimension to be
deleted.
Conditions:
- F ∈ S. F
S
;
D ∈ S.D
S
and
| D
S
| >= 2
Outputs:
S’ is the MDS from which the dimension D is
removed where:
- S’ = (Name
S
, Dom
S
, F
S
, D
S’
,
Func
S’
),
- D
S’
= D
S
\ {D},
- ∀ f ∈ F
S
; Func
S
’(f) =
Func
S
(f)
\ D.
- Attribute deletion
This operation deletes a strong or a weak attribute
from a hierarchy and removes it from the dimension.
The hierarchy identifier is the only attribute that
cannot be deleted.
Definition
The attribute deletion operation DelA deletes a
dimension attribute from a MDS. Its syntax is:
DelA (S, H
D
i
, A) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- H
D
i
=
(Name
H
, P
H
) is a hierarchy not having the
attribute A,
- A : is the attribute to be removed.
Conditions:
- A ∈ H
D
i
;
A ∉ (H
D
- H
D
i
) and A ≠ H
D
i
.p
1
Outputs:
S’ is the MDS from which the attribute A is
deleted.
- S’ = (Name
S
, Dom
S
, F
S
, D
S’
,
Func
S
),
- D
S
’ = {D
1
, D
2
, …, D’, …, D
N
} ;
D’ = (Nom
D
, A
D
’, H
D
’),
- A
D
’= A
D
\ {A},
- H
D
’= (Nom
H
, P
H
’
.
) ; P
H
’ = P
H
\ {A}.
- Fact deletion
This operation deletes a fact F, its measures and its
specific (not shared) dimensions from a constellation
schema.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
172

Definition
The fact deletion operation DelF deletes a fact
from a MDS. Its syntax is:
DelF(S, F, Dim) = S’
Inputs:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS,
- F = (Name
F
, M
F
) is the fact to be deleted,
- Dim
=
{d
F
1
, d
F
2
,…, d
F
N
} is a set of dimensions
to which F can be associated.
Conditions:
- F ∈ S. F
S
;
| F
S
| >= 2 and Func(F) = Dim
F
Outputs:
S’ is the MDS from which we deleted the fact F
where:
- S’ = (Name
S
, Dom
S
, F
S’
, D
S’
,
Func
S’
),
- F
S’
= F
S
\ {F},
- D
S’
= D
S
\ Dim,
- Func
S
’(F) = ∅
4.3 Rename Operations
This operation renames a multidimensional element
by a meaningful name supplied by the user. It
preserves the established correspondence of the
renamed element with the data source and the
uniqueness of names constraint:
Nom
F
∩Nom
D
∩Nom
H
∩ Nom
1
MF
∩Nom
1
AD
= ∅.
4.4 Data Restitution
The restitution is performed through a function that
reproduces a MDS stored in a referential.
Definition
The display operation DisplayS visualizes a MDS
graphically. Its syntax is:
DisplayS (S)
Input:
- S = (Name
S
, Dom
S
, F
S
, D
S
,
Func
S
) is a MDS
stored in a referential.
Condition:
- S belongs to a referential
Output:
- S displayed as a multidimensional diagram.
5 IMPLEMENTATION
This section illustrates with examples the
functionalities of the interface we are currently
developing.
Figure 2 is the input XML file for our interface;
it describes the PURCHASE schema belonging to
the commercial domain. This file is issued from a
generation module not detailed here (c.f. Soussi and
al, 2005).
<?xml version="1.0" encoding="iso-8859-1"?>
<star name="S1" domain="Commercial">
<fact name="Purchase">
<measure name="Amount" />
<measure name="Qtity_purch" />
</fact>
<dimension name="Time">
<attribute name="IdT" />
<attribute name="Day" />
<attribute name="Month" />
<attribute name="Quarter" />
<attribute name="Semester" />
<attribute name="Year" />
<hierarchy name="HM1_time">
<parameter name="IdT" />
<parameter name="Day" />
<parameter name="Month" />
<parameter name="Quarter" />
<parameter name="Semester" />
<parameter name="Year" />
</hierarchy>
</dimension>
<dimension name="Supplier">
<attribute name="IdS" />
<attribute name="Social_name" />
<attribute name="City" />
<attribute name="Department" />
<attribute name="Region" />
<hierarchy name="HM1_Supplier">
<parameter name="IdS">
<week_attribute name="Social_name" />
</parameter>
<parameter name="City" />
<parameter name="Department" />
<parameter name="Region" />
</hierarchy>
</dimension>
</star>
Figure 2: XML Script describing a DM analyzing the fact
PURCHASE.
Figure 3 shows the tree relative to the XML
script, as displayed by our DM Schema explorer
module.
Figure 3: Tree visualizing the star of Figure 2.
Once displayed in a tree format, the MDS is
better understandable; consequently, the decisional
designer can now make some changes on it.
A second way to display a MDS is a graphical
diagram; it has the merit to be more expressive as it
is shown by Figure 4.
A GUI FOR DATA MART SCHEMA ALTERATION
173

Figure 4: S1: star schema of Figure 2 visualized according
to Golfarelli formalism.
To illustrate the use of our operations, we apply
those of Table 2 on the star schema S1.
Table 2: Examples of graphical operations on S1.
Operation Description
DelA (S1, Supplier,
Region
Supplier
)
Deletes the attribute Region
of the
Supplier dimension.
AddF (S1, Sale, Time)
Inserts a new fact (SALE,
Amount
Sale
, Qtity_sold
Sale
, Min
Sale
)
into S1. This fact shares the Time
dimension with the fact PURCHASE.
AddD (S1, Sale, Client)
Adds the dimension (Client, IdC
Client
,
City
Client
, Department
Client
,
Region
Client
) to the fact SALE.
AddA (S1, Client,
Id
Client
, Age
Client
,
Slice
Client
)
Inserts new attributes into S1. This,
results the creation of a new
hierarchy as the following step
shows.
AddH (S1, Client,
H
2
Client
)
Adds the hierarchy H
2
Client
=<IdC
Client
,
Age
Client
, Slice
Client
> to Client
dimension.
DelM (S1, Sale, Min)
Deletes
M
in measure from SALE
f
act.
Figure 5 describes the results of the applied
operations on S1.
Figure 5: S2 graphical representation.
The addition of the fact SALE transforms S1 into
a constellation model since we obtain two facts
(PURCHASE and SALE) that share the common
dimension Time. It is the only operation that changes
the multidimensional model nature transforming a
star into a constellation.
6 CONCLUSION
In this paper, we defined a set of operations
necessary to MDS alteration. In order to validate our
proposals, we have implemented a GUI that
integrates these operations. The interface, currently
under finishing, allows the designer to visualize the
MDS as a tree by the DM schema explorer or as a
multidimensional diagram. Our operations can be
useful to the evolution of a DM schema.
REFERENCES
Bonifati A., Cattaneo F., Ceri S., Fuggetta A., Paraboschi
S., 2001. "Designing Data Marts for Data
Warehouses". ACM Transactions on Software
Engineering Methodology.
Feki J., 2004. "Vers une conception automatisée des
entrepôts de données : Modélisation des besoins
OLAP et génération de schémas multidimensionnels ".
8
th
Maghrebin Conference on Software Engineering
and Artificial Intelligence (MCSEAI’04), Sousse,
Tunisia, p. 473-485.
Golfarelli, M., Maio, D., and Rizzi, S., 1998. "The
Dimensional Fact Model: a conceptual model for data
warehouses". International Journal of Cooperative
Information Systems, vol. 7, n. 2&3.
Kimball, R., 1996. The Datawarehouse Toolkit. John
Wiley & Son, Inc.
Majdoubi J., Feki J., Gargouri F., 2005. "A Two-Phase
Approach for Multidimensional Schemes Integration",
ICEIS’05, Miami, USA.
Moody, D., Kortnik, M., 2000 . “From Enterprise Models
to Dimensional Models: A Methodology for Data
Warehouse and Data Mart Design”. DMDW’00,
Sweden.
Nabli A., Feki J., Gargouri F., 2005. "Adapting
Multidimensional Schemes to Data sources using
Algebraic Operators", The Seventeenth International
Conference on Software Engineering and Knowledge
Engineering, SEKE’05, Taipei, Taiwan, China.
Soussi A., Feki J., Gargouri F., 2005. "Approche semi-
automatisée de conception de schémas
multidimensionnels valides", 1
st
French day on the
Data Warehouses and the On line analysis (EDA’05),
Lyon, French.
Tryfona N., Busborg F., and Christiansen J. G. B., 1999.
"StarER: A Conceptual Model for Data Warehouse
Design". Proceedings of the ACM DOLAP’99
Workshop, Missouri.
PURCHASE
Amount
Qtity_purch
TIME
Mont
h
Day I
d
T Quarte
r
Semester
Yea
r
SUPPLIER
SALE
Amount
Qtity_sold
CLIENT
City
Department
Regio
n
IdC
Name
City
Department
IdS
Social_Name
Age
Slice
PURCHASE
Amount
Qtity_purch
TIME
Month Day IdT Quarte
r
Semester
Yea
r
SUPPLIER
Region
Cit
y
Departmen
t
IdS
Social_Name
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
174
