
COLLABORATIVE FILTERING BASED ON
CONTENT ADDRESSING
Shlomo Berkovsky, Yaniv Eytani, Larry Manevitz
Computer Science Department,University of Haifa, Israel
Keywords: Collaborative Filtering, Recommender Systems, Content-Addressable Systems.
Abstract: Collaborative Filtering (CF) is one of the most popular recommendation techniques. It is based on the
assumption that users with similar tastes prefer similar items. One of the major drawbacks of the CF is its
limited scalability, as the complexity of the CF grows linearly both with the number of available users and
items. This work proposes a new fast variant of the CF employed over multi-dimensional content-
addressable space. Our approach heuristically decreases the computational effort required by the CF
algorithm by limiting the search process only to potentially similar users. Experimental results demonstrate
that our approach is capable of generate recommendations with high levels of accuracy, while significantly
improving performance in comparison with the traditional implementation of the CF.
1 INTRODUCTION
The quantity of available information grows rapidly
and exceeds our cognitive processing capabilities.
Thus, there is a pressing need for intelligent systems
providing services tailored to users' real needs and
interests. Recommender Systems (RSs) (Resnick &
Varian, 1997) are one of the commonly used
approaches to address this problem. These systems
assist users to select a suitable item among a set of
potential selectable items through applying statistical
and knowledge discovery techniques (Sarwar et al,
2000). RSs are used in different domains, such as,
movies (Good et al, 1999), jokes (Goldberg et al,
2001), music (Aguzolli et al, 2002), and many
others.
Collaborative Filtering (CF) (Herlocker et al,
1999) is probably one of the most familiar and most
widely-used techniques to generate
recommendations in RSs. It relies on the assumption
that people who agreed in the past will also agree in
the future (Shardanand & Maes, 1995). The input for
the CF algorithm is a matrix of users' ratings on a set
of items, where each row represents ratings of a
single user and each column represents ratings on a
single item. CF aggregates the ratings to recognize
similarities between users and generates new
recommendation for an item by weighting the
ratings of similar users on the item.
CF algorithm is typically partitioned to three
generic stages: (1) Similarity Computation:
weighting all the users with respect to their
similarity with the active user (i.e., the user whose
ratings are predicted), (2) Neighborhood Formation:
selecting the most similar users for the prediction
generation, and (3) Prediction Generation:
computing the prediction by weighting the ratings of
the selected users.
A major drawback of CF is its limited scalability.
The stages of Similarity Computation and
Neighborhood Formation require comparing an
active user with all the other users over all the
available ratings. Hence, the complexity of the CF
grows both with the number of users and items in
the ratings matrix. For a matrix containing ratings of
M users on N items, computational complexity of the
above stages is O(MN). This poses a problem in
real-life systems, where the recommendations are
generated using millions of ratings on thousands of
items, e.g., Web-based RSs. Although previous
studies, such as (Breese et al, 1998), (Goldberg et al,
2001), and (Chee et al, 2001) tackle the issue of
reducing the computational effort required by the
CF, it remains one of the most important issues in
CF research.
In this work we develop a fast heuristic variant
of the CF algorithm that decreases the computational
effort required by the Similarity Computation and
the Neighborhood Formation stages. The basic
91
Berkovsky S., Eytani Y. and Manevitz L. (2006).
COLLABORATIVE FILTERING BASED ON CONTENT ADDRESSING.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 91-98
DOI: 10.5220/0002454100910098
Copyright
c
SciTePress

conjecture of the heuristic algorithm is that losing
general completeness of the exhaustive search (1)
has a minor negative effect on the accuracy of the
predictions, but (2) significantly decreases the
required computational effort. Thus, it provides a
scalable approach, applicable to real-life scenarios
with high number of users and items.
The proposed heuristic approach is based on a
notion of content-addressable data management
(Ratnasamy et al, 2001), providing an adaptive
topology for mapping of users' profiles to a multi-
dimensional space. This mapping implicitly clusters
similar users and limits the Similarity Computation
and the Neighborhood Formation stages to a
heuristic search among highly similar users only.
Experimental evaluation of the proposed
approach demonstrates high efficiency and good
accuracy of the proposed algorithm, in comparison
with the traditional (exhaustive) KNN search. The
algorithm is also highly scalable with the number of
nearest neighbors to be found.
The rest of the paper is organized as follows.
Section 2 surveys the works focusing on the CF and
the required computational effort reduction. Section
3 describes CAN, Peer-to-Peer content-addressable
platform for decentralized data management. Section
4 describes the decentralized storage of users'
profiles over CAN platform and elaborates on the
proposed variant of the CF over CAN. Section 5
presents and analyzes the experimental results.
Finally, section 6 lists our conclusions and presents a
list of open questions for future research.
2 COLLABORATIVE FILTERING
Collaborative Filtering (CF) is probably one of the
most familiar and widely-used recommendation
techniques. An input for the CF is so-called ratings
matrix, where each user is represented by a set of
ratings given on various items, and each item is
represented by a set of ratings given by the users.
CF requires similarity metric between users to be
explicitly defined. The state-of-the-art CF systems
exploit three similarity metrics: Cosine Similarity 0,
Mean Squared Difference (MSD) (Pennock et al,
2000), and Pearson correlation (Sarwar et al, 2000).
This work focuses on the MSD, computing the
degree of similarity between users x and y by:
2
||
,,
1
,
()
||
xy
xi yi
i
xy
RR
sim
xy
=
−
=
∑
∩
∩
(1)
where |x∩y| denotes the number of items rated by
both users, and R
x,i
denotes the rating of user x on
item i. In some sense, sim
x,y
can be considered as the
dissimilarity of the users, as the lower the result of
the MSD computation, the greater is the real
similarity of the users.
Prediction P
a,j
for the rating of the user a on item
j is computed as a weighted average of the ratings of
his K most similar users, i.e., K nearest neighbors,
by:
'
,,
'
1
,
,
1
()
||
K
kj k ak
k
aj a
K
ak
k
R
Rsim
PR
sim
=
=
−⋅
=+
∑
∑
(2)
where R
x,y
denotes the rating of user x on item i, R
z
'
denotes the average rating of user z, and sim
v,u
denotes the level of similarity between users v and u.
The Similarity Computation stage of the CF
requires comparing the active user with every other
user in the system. For a ratings matrix storing the
ratings of M users on N items, the computational
complexity of the Similarity Computation stage is
O(MN). This points on the poor scalability of the
Similarity Computation stage, as the complexity
grows linearly with both the number of users and the
number of items in the matrix.
2.1 Reducing the Computational
Effort Required by the CF
Many works deal with decreasing the computational
effort required by the CF. In general, it is achieved
either by preprocessing the ratings matrix, or by
distributing the computationally intensive stages of
the CF among multiple machines.
Various preprocessing techniques for decreasing
the computational effort required by the CF (e.g.,
correlation coefficients, vector-based similarity, and
statistical Bayesian methods) are discussed and
analyzed in (Breese et al, 1998). Another technique,
exploiting pre-clustering of the ratings matrix, is
discussed in (Goldberg et al, 2001). There, principal
component analysis is used to find two
discriminative dimensions of the ratings matrix and
all the vectors are projected onto the resulting plane.
This inherently partitions the users to clusters or
neighborhoods, which are further used to generate
the recommendations. In (Chee et al, 2001), the
authors use a tree-like data structure and apply a
divide-and-conquer approach using an iterative K-
means clustering to group the users. This leads to
smaller and more homogeneous clustering of users
for the recommendations generation stage.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
92

An alternative approach is to distribute the CF
and the required computational effort among the
users, such that every user independently computes
its similarity with the active user. This is initially
proposed in (Tveit, 2001) and elaborated in (Sarwar
et al, 2001). The latter also develops a detailed
taxonomy of the CF distribution approaches and
presents implementation frameworks for different
application domains. PocketLens project (Miller et
al, 2004) compares five decentralized distributed
architectures for the CF. The experiments show that
performance of the decentralized mechanism is
similar to the performance of the centralized CF,
while it provides increased robustness and security.
Further improvements to the decentralized CF
are discussed in (Han et al, 2004) that proposes
Peer-to-Peer platform for decentralized management
of user profiles. However, it approximates the
identification of the most similar users, and
therefore, the accuracy of the prediction is reduced.
This work loosely bases on the ideas of CAN
(Ratnasamy et al, 2001), content-addressable Peer-
to-Peer platform. We implement a fast heuristic
variant of the CF, using CAN-like multi-dimensional
space for maintaining connectivity of similar users.
This allows to significantly decrease the
computational effort required by the Similarity
Computation and Neighborhood Formation stages
through limiting the search process to a search
among highly similar users only.
3 CONTENT-ADDRESSABLE
DATA MANAGEMENT
This section present the general architecture of CAN
(Ratnasamy et al, 2001), scalable decentralized data
management platform. In CAN, the users are
represented by nodes in virtual N-dimensional
coordinate space. Each node maintains an N-
dimensional subspace, called a zone. For example,
consider a 2-dimensional space partitioned to 3
zones, maintained by the users A, B, and C (figure 1-
left).
Figure 1: 2-Dimensional CAN Space.
Two nodes are called neighbors if their
coordinate spans overlap along N-1 dimensions and
adjoin along one dimension (e.g., nodes A and B in
figure 1-left). To maintain connectivity, each node
maintains a table of pointers to its neighbors. CAN's
routing algorithm greedily forwards messages to the
nodes that are closer to the target node than the
current node (the distance metric exploited is the
discrepancy in the address space). Thus, the
messages are routed between any pair of CAN nodes
in a logarithmic number of hops.
Also, CAN provides connectivity maintenance
algorithm, stable to sporadic joins and departures of
nodes. When a new node is inserted, it must be
given its own zone. This is done by splitting a zone
of one of the existing neighbors according to the
following steps: (1) the new node finds an existing
networks node, (2) the new node is routed to the
target zone that will be split, and (3) the target zone
is split and the neighbors of the new zone are
updated to maintain connectivity and facilitate
routings. Note, that only a subset of neighbors of the
zone that was split is affected by the insertion of a
new node.
The issue of splitting the target zone (i.e., how to
split the existing zone, where the new node was
mapped to) is one of the important issues affecting
the performance of CAN. A number of policies are
proposed, analyzed and compared in (Ratnasamy et
al, 2001). The simplest policy for the zones splitting
is so-called ordered splitting. According to this
policy, the number of dimension across which a
zone is split, iteratively increases from 1 to N.
For example, consider a node D joining CAN
space (figure 1-middle). Assuming that the zone of a
node C will be split, D is routed to C, and the zone is
split across the horizontal dimension (i.e., the next
split of the zones C or D will be performed across
the vertical dimension and so forth). Finally, D
notifies its neighbors, i.e., the nodes B and C, about
the new node and the neighbors' pointers are
updated. Note that in this case, only the zone that
was split (C), and part of its neighbors (only B) are
affected by the join of a node D, whereas other
nodes are not affected.
Disconnections of nodes are handled in a similar
manner. Disconnecting node finds a neighbor node
that will take the responsibility for its zone, and
updates other neighbors about the departure. For
example, consider node B disconnecting (figure 1-
right), and assume node D taking the responsibility
for the zone previously managed by B.
Thus, CAN provides a decentralized platform,
supporting (1) dynamic space partitioning and zones
allocation, (2) efficient routing algorithm, and (3)
connectivity maintenance algorithm over virtual N-
COLLABORATIVE FILTERING BASED ON CONTENT ADDRESSING
93

dimensional coordinate space. Note that distributed
structure of CAN is not robust against sudden
departures of node, as fault-tolerance is not one of
the main goals of the platform. However, CAN
facilitates completely decentralized self-manageable
platform for content-addressable data management
in distributed environment.
4 CF OVER CONTENT-
ADDRESABLE SPACE
This work proposes a fast heuristic variant of the CF
algorithm. It uses content addressing architecture for
the purposes of optimizing traditional exhaustive
search to a search among highly similar users only.
Although our algorithm is heuristic by nature,
experimental results demonstrate that it facilitates
efficient search process without hampering the
accuracy of the generated recommendations.
4.1 Mapping User Profiles
The input for the CF algorithm is a matrix of users'
ratings on items, where each row (vector) represents
the ratings of a single user and each column
represents the ratings on a single item. The total
number of items (N) defines an N-dimensional
space, where the coordinates range in each
dimension corresponds the range of ratings on the
respective item.
To handle the ratings matrix in content-
addressable manner, we map it to CAN-like space.
Each rating is projected using uniform injective
mapping onto the appropriate dimension, such that
the whole vector of length N is mapped to a single
point in N-dimensional space. Thus, every user is
represented in the space by a single node (whose
location corresponds the set of ratings given by the
user), and the respective zone (storing a list of
neighbor zones). Users (through their ratings
vectors) can be dynamically inserted and removed,
since connectivity maintenance algorithm guarantees
that the structure remains connected regardless of
joins and disconnections of the nodes.
Deciding on the zones split policy affects the
evolving structure of the ratings vectors. In our
implementation, we used the above mentioned
ordered splitting policy. This policy may be sub-
optimal in terms of the number of neighbor zones,
resulting in less efficient algorithm, i.e., more
comparisons or finding less similar neighbors.
However, our experimental results indicate that the
use of this simple policy considerably increases the
efficiency of KNN, in comparison with traditional
exhaustive search. Evaluating other splitting policies
is beyond the scope of this work.
In addition to the guaranteed connectivity,
content-addressable space inherently clusters similar
users. Thus, the distance between two similar users
(in our case, according to the MSD similarity metric)
is lower than the distance between two arbitrary
users. This is achieved through the use of injective
mapping, preserving users' similarity while inserting
the ratings vectors into the content-addressable
space. The next subsection shows a use of the
inherent clustering for the purpose of developing fast
heuristic variant of the CF algorithm.
4.2 Heuristic Neighbors Search
The Neighborhood Formation stage of the CF over
the evolving N-dimensional space can be
schematically described as heuristically expanding
breadth-first search. The algorithm for finding K
Nearest Neighbors (KNN) of a user x is briefly
explained by the following pseudo-code. It uses two
lists of size K: (1) CANDIDATES – list of candidates
for nearest neighbors, and (2) KNN – list of real
nearest neighbors. In principle, the algorithm needs
the CANDIDATES list only, as the KNN list is
completely static. For the sake of clarity, we show
an algorithm that uses two lists.
K_Nearest_Neighbors (user x)
(1) let KNN and CANDIDATES be lists of
size K, initially empty
(2) map(x) into the CAN space
(3) foreach u
∈
map(x)
∪
neighbors(map(x))
(4) compute distance(x,u)
(5) insert u into CANDIDATES, s.t.
CANDIDATES is sorted by distances
(6) for i=1 to K
(7) choose v from CANDIDATES,
s.t. distance(x,v) is smallest
(8) for each w in neighbors(v) s.t.
distance(x,w) is not computed yet
(9) compute distance(x,w)
(10) insert w into CANDIDATES, s.t.
it remains sorted by distances
(11) move v from CANDIDATES to KNN
(12)return KNN
Initially, the algorithm pretends to map the active
user x to its location in the N-dimensional space
(step 2). Next, the algorithm identifies the zone x is
mapped to, and its neighbors, i.e., users managing
the neighbor zones (step 3). For each of these zones,
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
94
the degree of similarity, i.e., the distance between x
and the relevant node, is computed. The neighbor
node is inserted into the CANDIDATES list such that
the candidate nodes are sorted according to their
distances from the active user x (steps 4 and 5).
Then the algorithm iteratively performs the
following operations:
• Selects v, the nearest neighbor stored in the
CANDIDATES list (step 7),
• Identifies the neighbors of v that are not in the
CANDIDATES list yet, computes their distances
from x, and inserts them to the CANDIDATES,
while keeping the list sorted (steps 8, 9, and 10).
• Removes v from the CANDIDATES list and
inserts it to the KNN list.
Finally, the algorithm returns the resulting KNN list
(step 12).
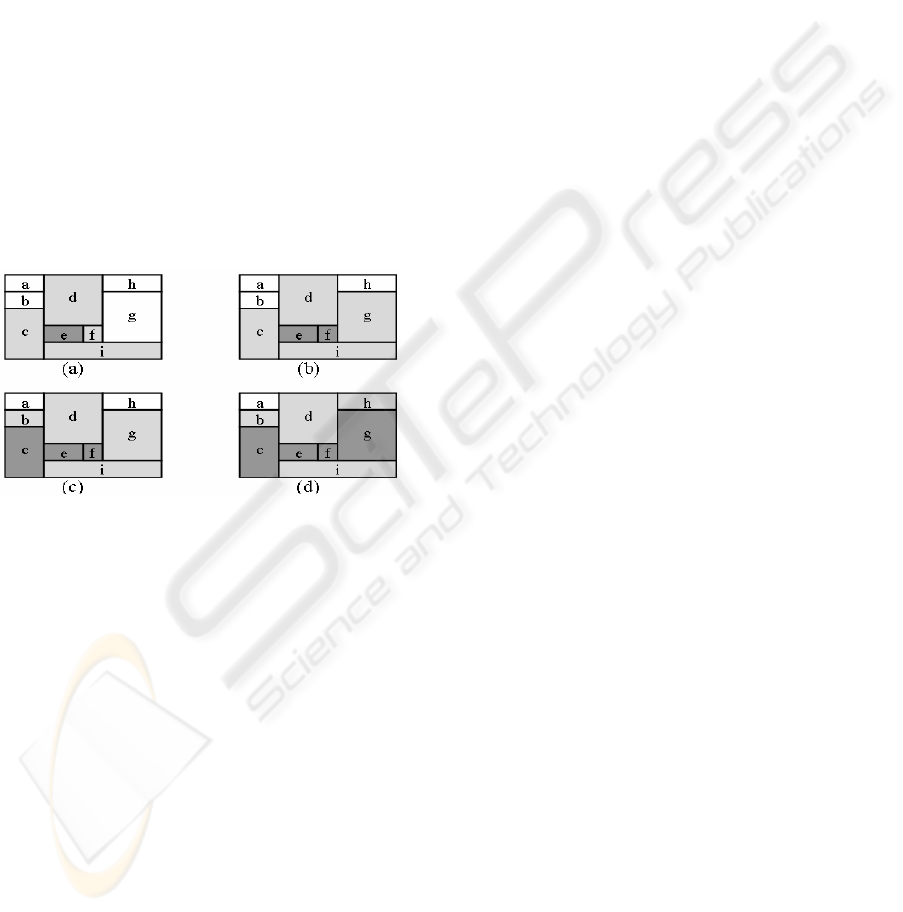
Consider an example execution of the KNN
search as illustrated in figure 2. The initial structure
of 2-dimensional space is depicted in figure 2a.
Assume that the active user is mapped to the zone e.
Figure 2: Stages of KNN Search over 2-D CAN Space.
Thus, e and its neighbors, i.e., nodes managing
the zones c, d, f, and i, are the first candidates for the
being nearest neighbors and they are added to the
CANDIDATES list. Assume that the node managing
the zone e is the closest one. It is moved from the
CANDIDATES list to the KNN list (figure 2a). Since
all the neighbors of e are already known, the next
closest neighbor is chosen among its neighbors.
Assume that the next closest neighbor is the node
managing the zone f. It is moved from the
CANDIDATES list to the KNN list, and its only new
neighbor, node managing g, is added to the
CANDIDATES list (figure 2b). The next closest
neighbor is from the zone c, adding the node
managing the zone b to the CANDIDATES list
(figure 2c). Assume that the next closest neighbor is
the node managing g (not a neighbor of e). It adds
the node managing the zone h to the CANDIDATES
list (figure 2d). This process is iteratively repeated
until the KNN list contains K nearest neighbors.
The proposed algorithm reduces the
computational effort required by the Similarity
Computation and the Neighborhood Formation
stages, in comparison with the traditional CF
algorithm, where an active user is compared with all
the available users. Conversely, the proposed
heuristic algorithm compares the active users with
potentially similar users only.
Since every user in the N-dimensional space
continuously maintains an updated list of neighbors,
any neighbor of a given user can be accessed
through a single network hop. This is true regardless
of the distance between the neighbors. Thus, the
algorithm will also work in sparse spaces, where the
distance between neighbors in the underlying
network might be very high.
5 EXPERIMENTAL RESULTS
In the experimental part of our work we used Jester
dataset of jokes (Goldberg et al, 2001). Jester is
Web-based jokes RS, containing 4.1 millions of
ratings (from -10.00 to +10.00) of 73,421 users on
100 jokes. We chose a subset of 14,192 users that
rated all 100 jokes to get a dense matrix of complete
vectors where every value corresponds to actual
rating. We implemented a centralized simulation of
a 100-dimensional space (space dimension equals to
the number of rated jokes) and inserted the above
14,192 users into the space. Insertions of the users
were done using the ordered splitting policy.
5.1 Scalability
These experiments were designed to evaluate the
scalability of the proposed variant of KNN. The
efficiency of CAN-based KNN is measured by the
number of comparisons performed during the
Neighborhood Formation stage of the CF.
In the first experiment we measured number of
comparisons performed during the search. We
gradually increased the number of users (M) in the
system from M=1,000 to M=14,000. For each M, we
computed the number of comparisons performed in
the traditional exhaustive KNN search and in CAN-
based variant of KNN. Both searches aimed to find
K=5 nearest neighbors. For each value of M, the
experiments were repeated 1,000 times for different
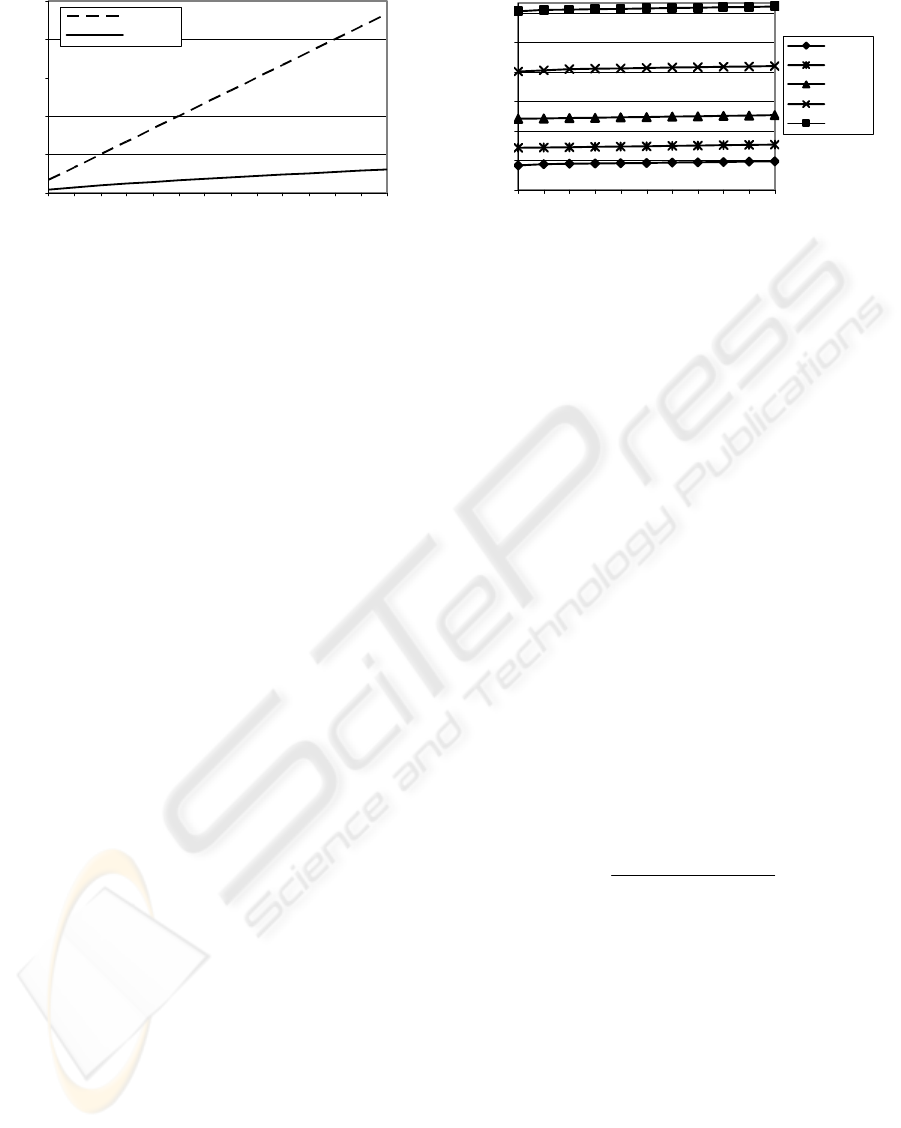
active users. The results are shown on Figure 3.
COLLABORATIVE FILTERING BASED ON CONTENT ADDRESSING
95
0
3000
6000
9000
12000
15000
1000 3000 5000 7000 9000 11000 13000
M
number of comparisons
exhaustive
CAN-based
Figure 3: Average Number of Comparisons vs. M.
As expected, the number of comparisons in
CAN-based KNN is significantly lower than in
traditional KNN and it grows at a logarithmic-like
manner with the number of users. This is explained
by the fact that in CAN-based KNN the active user
is compared only with a subset of highly similar
users (located in a close vicinity in content-
addressable space), whereas in traditional KNN it is
exhaustively compared with all other users.
To achieve a better understanding of
comparison-based scalability of the proposed
approach, we computed the ratio between the
number of comparisons in CAN-based KNN and the
number of comparisons in traditional (exhaustive)
KNN. This ratio was computed for different values
of M. The results show that the ratio steadily
decreases with M. This allows us to conclude that
the proposed algorithm is applicable in large-scale
systems with high number of users and items, e.g.,
on the Web.
The second experiment evaluated the scalability
of CAN-based KNN with the number of nearest
neighbors (K) to be found. We gradually increased
the value of K from K=1 to K=50. For each value of
K, we measured the number of comparisons needed
to find K nearest neighbors for M=1,000, 2,000,
4,000, 8,000, and 14,000 users. For each value of M
and K, the experiments were repeated 1,000 times
for different active users. The number of
comparisons as a function of K for the above values
of M is shown on figure 4.
As can be clearly seen, the number of
comparisons in CAN-based KNN remains roughly
unchanged when K increases. This is explained by
the observation that most of the KNN users are
located in a close vicinity to the active user (this
characterizes a real-life naturally clustered data).
Thus, the similar users are discovered in the early
stages of the KNN search, while further expansions
contribute very few new similar users.
0
300
600
900
1200
1500
1800
1 5 10 15 20 25 30 35 40 45 50
K
number of comparisons
M=1000
M=2000
M=4000
M=8000
M=14000
Figure 4: Average Number of Comparisons vs. K.
Both experiments show good scalability of CAN-
based KNN with K. This means, that practical RSs
can use higher values of K, form a larger and more
reliable neighborhood, and generate more accurate
predictions with only a very minor computational
overhead.
5.2 Accuracy
The following experiments were designed to
evaluate the accuracy of the results obtained by the
proposed heuristic variant of KNN. In the first
experiment we compared the sets of users, i.e., the
neighborhoods, found by the traditional (exhaustive)
KNN and by CAN-based variant of KNN.
Let us denote by KNN
e
the set of users found by
the traditional exhaustive KNN search and by KNN
h
the set of users found by CAN-based heuristic
variant of KNN. Since CAN-based KNN is a
heuristic approach, a sub-optimal structure of zones
may lead to KNN
e
≠KNN
h
. As predictions are
produced by aggregating the ratings of similar users,
identifying the most similar user is critical for
producing an accurate prediction. Thus, we define
the accuracy of CAN-based search by:
(3)
The cardinality of the KNN
e
set was K=10, while
the cardinality of the KNN
h
set was gradually
increased from K'=1 to K'=100. The accuracy was
computed for M=1,000, 2,000, 4,000, 8,000 and
14,000 users. For each value of M and K', the
experiments were repeated 1,000 times for different
active users. Figure 5 shows the accuracy as a
function of K' for the above values of M.
||
||
eh
h
K
NN KNN
accuracy
KNN
∩
=
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
96

0
0.2
0.4
0.6
0.8
1
1 102030405060708090100
K'
accuracy
M=1000
M=2000
M=4000
M=8000
M=14000
Figure 5: Precision of CAN-based KNN.
As can be clearly seen, the curves behave
similarly and the accuracy increases with K', such
that for K'>50 it is over 0.9 for all the given values
of M. Previous experiments show that the algorithm
is highly scalable with K. Thus, retrieving a larger
set of users (i.e., higher values of K') leads to a
minor increase in the computational overhead.
Hence, it is reasonable to increase the number of
neighbors found by CAN-based search in order to
achieve higher accuracy and to generate better
recommendations.
We evaluated the quality of the neighborhood
found by CAN-based search by computing the
average similarity between the nearest neighbors and
the active user. This was compared to the average
similarity of neighborhood found in an exhaustive
manner. In addition, we evaluated the accuracy of
the recommendations through well-known Mean
Average Error (MAE) metric (Herlocker et al,
1999):
1
||
N
ii
i
p
r
MAE
N
=
−
=
∑
(4).
where N denotes the number of predicted items, and
p
i
is the predicted, and r
i
is the real rating on item i.
We gradually increased the number of users from
M=1,000 to M=14,000. For each value of M, we
compared the average similarity of heuristically
found neighbors with the average similarity of
exhaustively found neighbors for K=K'=10. We
also generated the recommendations basing on both
heuristically and exhaustively found neighborhoods.
For each value of M, the above experiments were
repeated 1,000 times for different active users. The
results of the average similarity comparison are
shown on figure 6, while MAE computation results
are shown on figure 7.
0.3
0.34
0.38
0.42
0.46
0.5
0.54
0.58
1000 3000 5000 7000 9000 11000 13000
M
average similarity
exhaustiv e
CAN-based
Figure 6: Average Similarity vs. M.
0.155
0.158
0.161
0.164
0.167
0.17
0.173
0.176
1000 3000 5000 7000 9000 11000 13000
M
MAE
exhaustive
CAN-based
Figure 7: MAE of the Recommendations vs. M.
Although both the similarity and MAE of CAN-
based search are higher (i.e., the neighbors are more
dissimilar and the accuracy is lower), the curves are
very close and the results are quite similar. Average
deviation of the similarities is 2.93% and of the
MAEs is only 0.38%. This allows us to conclude
that the proposed heuristic algorithm succeeds in
producing both accurate neighborhoods and
recommendations.
6 CONCLUSIONS AND FUTURE
RESEARCH
One of the major drawbacks of the state-of-the-art
CF implementations is their high computational
complexity, which grows linearly both with the
number of users and items in the system. In this
work we propose to heuristically decrease the
required computational effort through implementing
the CF over content-addressable CAN-like N-
dimensional space.
Experiments conducted over Jester dataset of
jokes ratings show that proposed heuristic algorithm
outperforms traditional exhaustive KNN search. Our
algorithm decreases the number of required
comparisons, while the ratio between the numbers of
comparisons steadily decreases with the number of
COLLABORATIVE FILTERING BASED ON CONTENT ADDRESSING
97

users. For example, for 14,000 users the number of
comparisons was decreased by almost an order of
magnitude (by 87%). Other experiment shows that
the number of comparisons roughly remains
unchanged when K increases. This allows us to
increase the number of nearest neighbors to be
retrieved (and to improve the accuracy of the
prediction) with a very minor computational
overhead.
In the accuracy experiments we compare the
neighborhoods and the predictions found by CAN-
based KNN and by the traditional KNN. The found
neighborhoods are similar and the recommendations
are very close, which indicates on a high accuracy of
the proposed algorithm. In summary, comparing the
proposed heuristic KNN search with traditional
exhaustive search shows that our algorithm achieves
high accuracy (similar to the accuracy of the
traditional exhaustive search), while significantly
decreasing the required computational effort.
In this work, we assumed that user's ratings on
all the items are available. Thus, the mapping of the
ratings vectors to CAN space is straightforward.
However, this is unachievable in many real-life
scenarios, where an average user rates only a small
portion of the available items. In the future, we plan
to study CAN-based management of incomplete
vectors, where part of the ratings is missing. Using
statistical methods to complete the vectors through
predicting the missing ratings might be a promising
research direction.
In addition to decreasing the computational
effort, our algorithm can naturally be extended to
distribute it among multiple users. In traditional
implementations of the CF, the Similarity
Computation and the Neighborhood Formation
stages are performed in a single central location.
However, as the underlying CAN platform is
originally distributed Peer-to-Peer platform, it
inherently allows distributed and fully decentralized
storage of the ratings matrix. In future, we plan to
implement a distributed variant of the algorithm and
to investigate the distribution issues.
The current work is limited to the Mean Squared
Difference similarity metric, since the injective
mapping to a multi-dimensional CAN-like space
inherently supports it. However, for other metrics,
such as Cosine Similarity or Pearson correlation,
CAN space might be inappropriate and new types of
topologies and the respective mappings should be
developed. We plan to study other metrics and to
produce a general framework for efficient heuristic
Collaborative Filtering.
REFERENCES
Aguzzoli, S., Avesani, P., Massa, P., 1997, Collaborative
Case-Based Recommender System, in proceedings of
the ECCBR Conference.
Breese, J., Heckerman, D., Kadie, C., 1998, Empirical
Analysis of Predictive Algorithms for Collaborative
Filtering, in proceedings of the UAI Conference.
Chee, S.H.S., Han, J., Wang, K., 2001, RecTree: An
Efficient Collaborative Filtering Method, in
proceedings of the DaWaK Conference.
Goldberg, K., Roeder, T., Gupta, D., Perkins, C., 2001,
Eigentaste: A Constant Time Collaborative Filtering
Algorithm”, in Information Retrieval Journal, vol.
4(2).
Good N., Schafer, J.B., Konstan, J.A., Borchers A.,
Sarwar, B., Herlocker, J., Riedl, J., 1999, Combining
Collaborative Filtering with Personal Agents for
Better Recommendations, in proceedings of the AAAI
Conference.
Han, P., Xie, B., Yang, F., Shen, R., 2004, A Scalable P2P
Recommender System Based on Distributed
Collaborative Filtering, in Expert Systems with
Applications Journal, vol. 27(2).
Herlocker, J.L., Konstan, J.A., Borchers, A., Riedl, J.,
1999, An Algorithmic Framework for Performing
Collaborative Filtering, in proceedings of the SIGIR
Conference.
Miller, B.N., Konstan, J.A., Riedl, J., 2004, PocketLens:
Toward a Personal Recommender System, in ACM
Transactions on Information Systems, vol.22 (3).
Pennock, D.M., Horvitz, E., Giles, C.L., 2000, Social
Choice Theory and Recommender Systems: Analysis
of the Axiomatic Foundations of Collaborative
Filtering, in proceedings of the AAAI Conference.
Ratnasamy, S., Francis, P., Handley, M., Karp, R.,
Shenker, S., 2001, A Scalable Content-Addressable
Network, in proceedings of the SIGCOMM
Conference.
Resnick, P., Varian, H.R., 1997, Recommender Systems, in
Communications of the ACM, vol. 40(3).
Sarwar, B., Karypis, G., Konstan, J., Riedl, J., 2000,
Analysis of Recommendation Algorithms for E-
Commerce, in proceedings of the EC Conference.
Sarwar, B.M., Konstan, J.A., Riedl, J., 2001, Distributed
Recommender Systems: New Opportunities for
Internet Commerce, in “Internet Commerce and
Software Agents: Cases, Technologies and
Opportunities”, Idea Group Publishers.
Shardanand, U., Maes, P., 1995, Social Information
Filtering: Algorithms for Automating "Word of Mouth,
in proceedings of the CHI Conference.
Tveit, A., 2001, “Peer-to-Peer Based Recommendations
for Mobile Commerce”, in proceedings of the WMC
Workshop.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
98
