
A LOAD BALANCING SCHEDULING APPROACH FOR
DEDICATED MACHINE CONSTRAINT
Arthur M. D. Shr, Alan Liu
Department of Electrical Engineering, National Chung Cheng University, Chia-Yi 621, Taiwan, R.O.C.
Peter P. Chen
Department of Computer Science, 298 Coates Hall, LSU, Baton Rouge, LA 70803, USA
Keywords: Load Balancing Scheduling, Dedicated Machine Constraint, Least Slack, Resource Schedule and Execution
Matrix, Semiconductor Manufacturing.
Abstract: The constraint of having a dedicated machine for photolithography process in semiconductor manufacturing
is one of the new challenges introduced in photolithography machinery due to natural bias. With this
constraint, the wafers passing through each photolithography process have to be processed on the same
machine. The purpose of the limitation is to prevent the impact of natural bias. However, many scheduling
polices or modeling methods proposed by previous research for the semiconductor manufacturing
production have not discussed the dedicated machine constraint. In this paper, we propose the Load
Balancing (LB) scheduling approach based on a Resource Schedule and Execution Matrix (RSEM) to tackle
this constraint. The LB scheduling approach is to schedule each wafer lot at the first photolithography stage
to a suitable machine according to the load balancing factors among machines. We describe the algorithm of
the proposed LB scheduling approach and RSEM in the paper. We also present an example to demonstrate
our approach and the result of the simulations to validate our approach.
1 INTRODUCTION
Semiconductor manufacturing systems are different
from the traditional manufacturing systems, such as
a flow-shops manufacturing system in assembly
lines or a job-shops manufacturing system. In a
semiconductor factory, one wafer lot passes through
hundreds of operations, and the processing
procedure takes a few months to complete. The
operations of semiconductor manufacturing
incrementally develop an IC product layer by layer.
Figure 1 shows the concept of the process flow of a
semiconductor manufacturing system, a re-entrant
production line (Kumar, 1993) (Kumar, 1994).
One of the challenges in the semiconductor
manufacturing systems is the dedicated
photolithography machine constraint which is
caused by the natural bias of the photolithography
machine. Natural bias will impact the alignment of
patterns between different layers. The smaller the
dimension of the IC products (wafers), the more
difficult they will be to align between different
layers. The wafer lots passing through each
photolithography stage have to be processed on the
same machine. The purpose of the limitation is to
prevent the impact of natural bias and to keep a good
yield of the IC product. Figure 2 describes the
dedicated machine constraint. When wafer lots enter
each photolithography operation stage, with this
constraint, the wafer lots dedicated to machine X,
they need to wait for machine X, even if there is no
wafer lot waiting for machine Y, which is idle. On
the other hand, when wafer lots enter into other
Figure 1: The process flow of semiconductor
manufacturing, a re-entrant line.
170
M. D. Shr A., Liu A. and P. Chen P. (2006).
A LOAD BALANCING SCHEDULING APPROACH FOR DEDICATED MACHINE CONSTRAINT.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 170-175
DOI: 10.5220/0002454801700175
Copyright
c
SciTePress

operation stages, without any machine constraints,
the wafer lots can be scheduled to any machine of A,
B or C as long as they become idle.
The constraint is the most important challenge to
improve productivity and fulfill the request for
customers as well as the main contributor to the
complexity and uncertainty of semiconductor
manufacturing. If we randomly schedule the wafer
lots to arbitrary photolithography machines at the
first photolithography stage, then the load of all
photolithography machines might become
unbalanced. This load balancing issue derived
mainly from the dedicated photolithography
machine constraint. This happens because once the
wafer lots have been scheduled to one of the
machines at the first photolithography stage, they
must be assigned to the same machine in the
subsequent photolithography stages until they have
passed the last photolithography stage. Therefore,
the short time of unexpected breakdown of one
machine will cause a pile up of many wafer lots
waiting for the machine and the situation makes the
machine critical to the factory.
Therefore, the unbalanced load among
photolithography machines will mean that some of
the photolithography machines will become idle and
remain so for a while, due to the fact that no wafer
lots can be processed, and the other will always be
busy while many wafer lots in the buffer limited to
this machine are awaiting processing. As a result,
the performance of the factory will have been
decreased and impacted. The wafer lots of a load
unbalancing factory usually need to be switched
from the highly congested machines to the idle
machines. It relies on experienced engineers to
manually handle alignment problem of the wafer lots
with a different situation off-line. It is inefficient to
determine one lot at a time which wafer lot and
machine need be switched. Moreover, this method
cannot meet the fast-changing market of the
semiconductor industry.
Motivated by the issues described above, we
propose a Load Balancing (LB) scheduling approach
based on a Resource Schedule and Execution Matrix
(RSEM) to tackle the dedicated machine constraint.
By selecting a wafer lot which has the maximum
waiting step and a wafer lot which has the smallest
load, the LB method could schedule each wafer lot
at first and unconstrained photolithography stage to
a suitable photolithography machine.
The paper is organized as follows: we describe
the related research in Section 2. Section 3 depicts
the algorithm of the proposed LB scheduling
approach. An example of semiconductor factory
applying LB scheduling approach is described in
Section 4. Section 5 shows the simulation results
that validated our approach. Section 6 discuses the
conclusion.
Figure 2: Dedicated machine constraint and load balancing
2 RELATED RESEARCH
By using a queuing network model, a “Re-Entrant
Lines” model has been proposed to provide the
analysis and design of the semiconductor
manufacturing system. (Kumar, 1993) (Kumar,
1994). These scheduling policies have been
proposed to deal with the buffer competing problem
in the re-entrant production line, wherein they pick
up the next wafer lot in the queue buffers when
machines are becoming idle. Wein’s research used a
Brownian queuing network model to approximate a
multi-class queuing network model with dynamic
control to the process in the semiconductor factory
(Wein, 1998). A special family-based scheduling
rule, Stepper Dispatch Algorithm (SDA-F), is
proposed to the wafer fabrication system (Chern and
Liu, 2003). SDA-F uses a rule-based algorithm with
threshold control and least slack principles to
dispatch wafer lots in photolithography stages. A
stochastic dynamic programming model proposed
for scheduling new wafer lot release and bottleneck
processing by stage in the semiconductor factory
(Shen and Leachman, 2003). This scheduling policy
incorporates analysis of uncertainties in products'
yield and demand.
Dynamic Scheduling System is a dynamic
artificial intelligent scheduling approach that focuses
on the most urgent unsolved problem (Hildum,
1994). Another research uses the Petri Net approach
to modeling, analysis, simulation, scheduling and
the control of the semiconductor manufacturing
system (Zhou and Jeng, 1998). Two researches
developed simulations to model the
photolithography process, one of them proposed a
Neural Network approach to develop an intelligent
scheduling method according to a qualifying matrix
and the lot scheduling criteria to improve the
performance of the photolithography machines
(Arisha and Young 2004). The other one is to decide
A LOAD BALANCING SCHEDULING APPROACH FOR DEDICATED MACHINE CONSTRAINT
171
the wafer lots assignment of the photolithography
machines at the time when the wafer lots were
released to manufacturing system to improve the
load-balancing problem (Mönch, et al. 2001).
3 RESOURCE SCHEDULE AND
EXECUTION MATRIX (RSEM)
The RSEM method consists of three modules Task
Generation, Resource Calculation, and Resource
Allocation modules. The first module is to model the
tasks for the scheduling system. For example, in the
semiconductor factory, the tasks are the procedures
of processing wafer lots, starting from the raw
material until the completion of the IC products. We
generate a two-dimension matrix for the tasks that
are going be processed by machines. One dimension
is reserved for the tasks t
1
, t
2
,…, t
n
, the other is to
represent the periodical time event (or step) s
1
,
s
2
,…,s
m
. Each task has a sequential pattern to
represent the resources it needed during the process
sequence from a raw material to a product. We
define each type resource as r
1
, r
2
, …, r
o
, where it
means a particular task needs the resources in the
sequence of r
1
and r
2
following that until r
o
is gained.
Therefore, the matrix looks as follows:
s
1
s
2
. . . . . s
j
. . s
m
t
1
r
1
r
2
r
3
.. .. .. r
k
. .. .. .. ..
t
2
r
3
r
4
.. .. r
k
.. .. .. .. ..
. .. ..
t
i
r
3
r
4
.. .. r
k
..
. . .
t
n
.. .. r
k
.. .. ..
The symbol, r
k
in the Matrix[t
i
, s
j
] is to represent
the fact that the task t
i
needs of the resource
(machine) r
k
at the time s
j
. If t
i
starts to be processed
at s
j
and the total step numbers of t
i
is p, we will fill
its pattern into the matrix from Matrix[t
i
, s
j
] to [t
i
,
s
j+p-1
]. All the tasks, t
1
,…t
n
, follow the illustration
above to form a task matrix in the task generation
module. To represent the dedicated machine
constraint in the matrix for this research, the symbol
r
k
x
, a replacement of r
k
, is to represent that t
i
has
been dedicated to number x of type k machine at s
j
.
The symbol w
k
is to represent the wait situation
when the machine r
k
cannot serve t
i
at s
j
. We will
insert this symbol in the Resource Allocation
module later.
The Resource Calculation module is to
summarize the value of each dimension as the
factors for the scheduling rules of the Resource
Allocation module. For example, we can acquire
how many steps t
i
needed to be processed by
counting task pattern of t
i
dimension in the matrix.
We can also realize how many wait steps t
i
has had
by counting w
k
from start step to current step of t
i
dimension in the matrix. Furthermore, if we count
the r
k
x
in s
j
dimension, we can know how many tasks
will need the machine m
x
of resource r
k
at s
j
.
Before we can start the execution of the
Resource Allocation module, we need to generate
the task matrix, obtain all the factors for the
scheduling rules, and build up the rules. The module
is to schedule the tasks to the suitable resource
according to the factors and predefined rules. To
represent the situation of waiting for r
k
; i.e., when t
i
can not take the resource of r
k
at the time s
j
, then we
will not only insert w
k
in the pattern of t
i
, but also
need to shift the following pattern to the next step in
the matrix. Therefore, we can obtain the updated
factor for how many tasks wait for r
k
at s
j
only if we
have counted w
k
by the dimension s
j
. We can also
obtain the factor for how many wait step that t
i
has
had only if we have counted w
k
, 1
≤
k
≤
o by t
i
dimension in the matrix
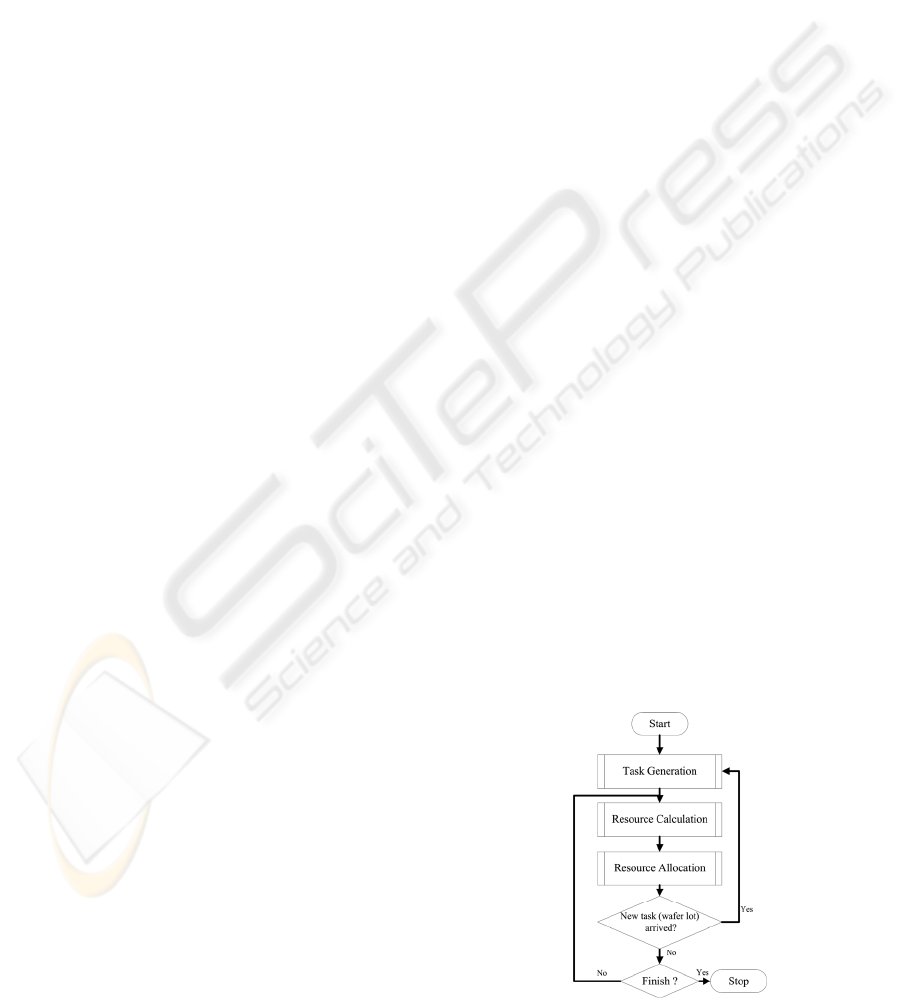
To better understand our proposed scheduling
process, the flowchart of RSEM is shown in Figure
3. The process of using the RSEM starts from the
Task Generation module and it will copy the
predefined task patterns of tasks into the matrix.
Entering the Resource Calculation module, the
factors for the tasks and resources will be brought
out at the current step. This module will update these
factors again at each scheduling step. The execution
of scheduling process is in the Resource Allocation
module. When we have done the schedule for all the
tasks for the current step, we will return to check for
new tasks and repeat the whole process again by
following the flowchart. We will exit the scheduling
process when we reaches the final step of the last
task if there is still no new task appended to the
matrix. After that, the scheduling process will restart
immediately when the new tasks arriving in the
system.
Figure 3: Scheduling flowchart.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
172

4 LOAD BALANCING
SCHEDULING APPROACH
After obtaining the process flow for customer
product from the database of semiconductor
manufacturing, we can use a simple program to
transform the process flow into our matrix
representation. There exist thousands of wafer lots
and hundreds of process steps in a typical factory.
We start from transforming the process pattern of
wafer lots into a task matrix. We let r
2
represent the
photolithography machine and r to represent non-
photolithography machines. The symbol r
2
x
in the
Matrix[i,j] is to represent the wafer lot t
i
need of the
photolithography machine m
x
at the time s
j
with
dedicated machine constraint, while r
k
x
(k
≠
2) is to
represent the wafer lot t
i
need of the machine type k
and the machine m
x
at s
j’
(j
≠
j’) without dedicated
machine constraint. There is no assigned machine
number for the photolithography machine before the
wafer lot has passed first photolithography stage.
Suppose that the required resource pattern of t
1
is as
follows: r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
2
r
4
r
5
r
6
r
7
r
8
r
9
r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
3
r
2
r
8
r
9
, and
starts the process in the factory at s
1
. We will fill its
pattern into the matrix from Matrix[t
1
,s
1
] to
Matrix[t
1
,s
25
], which indicates that the total number
of the steps for t
l
is 25. The following matrix shows
the pattern of t
1
. The wafer lot t
2
in the matrix has
the
same required resource pattern as t
1
but starting at s
3
.
The wafer lot t
i
in the matrix starts from s
8
, and then
it requires the same type resource, the
photolithography machine, but does not have the
same (number) machine at s
10
. This represents that t
2
needs the machine m
1
, while t
i
has not been
dedicated to any machine yet. Moreover, two tasks,
t
2
and t
i
might compete with the same resource r
4
at
s
11
if the resource of r
4
is not enough for them at s
11
.
The definitions and formulae of these factors for
the LB scheduling approach in the Resource
Calculation module are as follows:
W: wafer lots in process,
P: numbers of photolithography machines,
K: types of machine (resource)
(1) Required resource (machine):
(1.1) How many wafer lots will need the photolithography
machine m
x
at s
j
(with dedicated machine constraint):
PxrstMatrixsrRR
x
Wt
jij
x
i
≤≤=
∑
=
∈
1 ,],[),(
22
(1.2) How many wafer lots will need the other k type
machine at s
j
(without dedicated machine constraint):
KkkrstMatrixsrRR
k
Wt
jijk
i
1 ,2,],[),( ≤≤≠=
∑
=
∈
(2) Count step:
(2.1) How many wait steps the t
i
has had before s
j
:
KkwstMatrixtWaitStep
stepcurrent
startj
kjii
≤≤
∑
==
=
1 ,],[)(
(2.2) How many steps t
i
will have.
∑
≠=
=
stepend
startj
jii
stMatrixtSteps
""],[)(
(3) The load factor of machine m
x
, wafer lots
×
remanding
photolithography stages
∑
=
=
∈Wt
xiiijx
i
mtpmtRtsmLoad })(|)(*{),(
(3.1) How many remaining photolithography stages for t
i
:
PxrstMatrixtR
stepend
currentj
x
jii
≤≤
∑
==
=
1 ,],[)(
2
(3.2) pm(t
i
): dedicated photolithography machine number
of t
i
:
Load is defined as the wafer lots limited to
machine m multiple their remaining layers of
photolithography stage. Load is a relative parameter,
representing the load of the machine and wafer lots
limited to one machine compared to other machines.
The larger load factor means that the more required
service from wafer lots has been limited to this
machine.
The LB scheduling approach uses these factors
to schedule the wafer lot to a suitable machine at the
first photolithography stage which is the only
photolithography stage without the dedicated
constraint. Suppose we are currently at s
j
, and the
LB scheduling system will start from
photolithography machine. We check if there is any
wafer lot which is waiting for the photolithography
machines at the first photolithography stage. LB will
assign the m
x
with smallest Load(m
x
, s
j
) for them one
by one. After that, these wafer lots have been
dedicated a photolithography machine. For each m
x
,
LB will select one of the wafer lots dedicated to m
x
which has the largest WaitStep(t
i
) for it. Load(m
x
, s
j
)
of m
x
will be updated after these two processes. The
other wafer lots dedicated to each m
x
which can not
be allocated to the m
x
at current step s
j
will insert a
w
2
for them in their pattern. For example, at the step
s
10
, t
i
has been assigned to m
1
, therefore, t
i+1
will
have a w
2
being inserted into at s
10
, and then all the
following required resource of t
i+1
will shift one
step.
s
1
s
2
s
3
s
4
s
5
s
6
s
7
s
8
s
9
s
10
s
11
s
12
s
13
s
14
s
15
s
16
s
17
s
18
s
19
s
20
s
21
s
22
s
23
s
24
s
25
.. .. s
j
.. s
m
t
1
r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
2
r
4
r
5
r
6
r
7
r
8
r
9
r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
3
r
2
r
8
r
9
.
t
2
r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
2
1
r
4
r
5
r
6
r
7
r
8
r
9
r
1
r
3
r
2
r
4
r
5
r
6
r
7
r
3
r
2
r
8
r
9
t
i
r
1
r
3
r
2
r
4
r
6
r
5
.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. ..
..
.. ..
A LOAD BALANCING SCHEDULING APPROACH FOR DEDICATED MACHINE CONSTRAINT
173

The following matrix shows the situation. All the
other types of machine will have same process
without need of being concerned with the dedicated
machine constraint. Therefore, we assigned one of
the wafer lots which has the largest WaitStep(t
i
),
then the second largest one, and so on for each
machine r
k
. LB will insert a w
k
for the wafer lots do
not be assigned to machines r
k
at current step.
Therefore, WaitStep(t
i
) is to represent the delay
status of t
i
.
s
9
s
10
s
11
s
12
s
13
s
14
.. .. s
j
.. s
m
.. ..
t
i
..
r
2
1
r
4
r
5
r
6
r
7
.. ..
t
i+1’
..
w
2
r
2
1
r
4
r
6
r
5
.. .. .. ..
..
↑ → →
→ →
We assume that all the resource types for the
wafer lots will have the same process time in this
example, i.e., all the steps have the same time
duration. The assumption simplifies the real
semiconductor manufacturing system and helps us
focus on the issue of the dedicated machine
constraint. In fact, it is not difficult to approach the
real cases on a smaller scale time step. Another issue
is that the machines in the factory have capacity
limitation due to the capital invention, which is the
resource constraint. How to make the most profit for
the invention mostly depends on optimal resource
allocation techniques. However, most scheduling
polices or methods can provide neither the exact
allocation in accepted time, nor a robust and
systematic resource allocation strategy. We use the
RSEM to represent complex tasks and allocate
resources by the simple matrix calculation. This
reduces much of the computation time for the
complex problem.
Our LB scheduling system provides two kinds of
functions. One is that we can follow the predefined
rules from expert knowledge to obtain the resource
allocation result at each step quickly by the factors
summarized from task matrix. The other is that we
could predict the bottleneck or critical situation
quickly by executing proper steps forward. This can
also evaluate the predefined rules to obtain better
scheduling rules for the system at the same time.
5 SIMULATION RESULT
We have done two types of simulations for a Least
Slack (LS) time scheduling policy and our LB
scheduling method. The LS time scheduling has
been developed in the research, Fluctuation
Smoothing Policy for Mean Cycle Time (FSMCT)
(Kumar and Kumar, 2001) in which the FSMCT is
for re-entrant production lines. The entire class of
LS policies has been proven stable in a deterministic
setting (Lu and Kumar, 1991, and Kumar, 1994).
The LS scheduling policy sets the highest priority to
a wafer lot whose slack time is the smallest in the
queue buffer of one machine. When the machine is
going to idle, it will select the highest priority wafer
lot in the queue buffer to service next. However, the
simulation result shows that our proposed LB is
better than the LS method. For simplifying the
simulation to easily represent the scheduling
methods, we have made the following assumptions:
(1) Each wafer lot has the same process steps and
quantity.
(2) All photolithography and other stages have the same
process time.
(3) There is no breakdown event in the simulations.
(4) There is unlimited capacity for non-photolithography
machines.
The simulations are to use two photolithography
machines and 200 wafer lots. Each wafer lot in the
first simulation has 28 steps, and 5 of them are
photolithography stages. While each wafer lot in the
second simulation has 40 steps and 9 of them are
photolithography stages. In the following two
simulation patterns, r represents the non-
photolithography stage; and r
2
the photolithography
stage. The wafer lot t
2
starts to process in the factory
when t
1
has passed two steps (s
3
). t
3
starts when t
1
has passed three steps (s
4
) . We simulate the wafer
arrival rate between two wafer lots as a Poisson
distribution.
Simulation I: tasks matrix
s
1
,…………………………………………………………..s
m
t
1
:rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rr
t
2
: rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rr
t
3
: rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rr
:
t
200
: :
Simulation II: tasks matrix
s
1
,……………………………………………………………s
m
t
1
:rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rr
t
2
: rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rr
t
3
: rrr
2
rrrrr
2
rrrrrrrrr
2
rrrrrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rrr
2
rr
:
t
200
: :
We applied the LS and LB method for these two
photolithography machines to select the next wafer
lot to process in the simulations. When the wafer lot
needs to wait for its dedicated machine, we insert a
“w” in the process pattern of the wafer lot to
represent the situation. After completing the
simulations, we count the pattern of wafer lots to
obtain how much time they have used. The
simulation result is shown in Figure 4.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
174
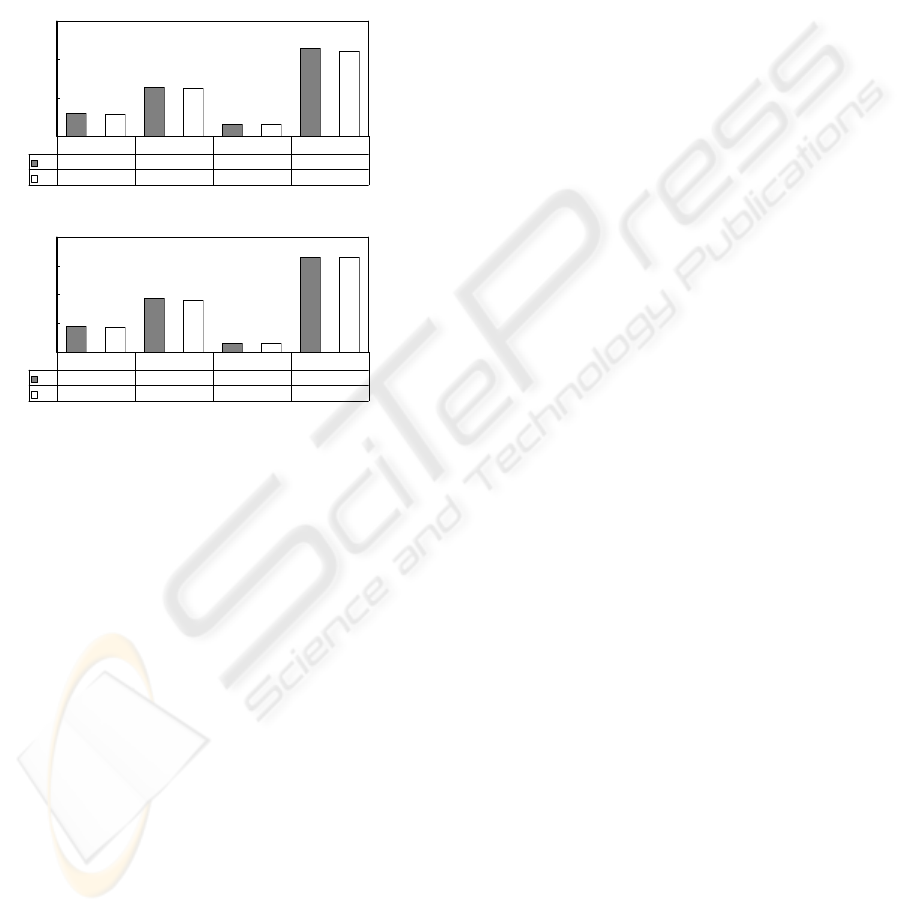
Comparing the mean of cycle time, the LS
method has an average 128.52 steps in simulation I
and 371.64 steps in simulation II. The LB method
has an average 125.63 and 356.50 steps in
simulation I and II. LB is better than LS 2.30% in
simulation I and 4.25% in simulation II. For the
deviation of steps of all wafer lots in these two
simulations, the LB approach is better than the LS
approach.
Simulation I
30
228
56.62
125.63
30
222
58.50
128.52
0
100
200
300
LS
58.50 128.52 30 228
LB
56.62 125.63 30 222
σ Mean Min Max
Simulation II
178.73
59
661
356.50
59
656
371.64
173.30
0
200
400
600
800
LS
178.73 371.64 59 661
LB
173.30 356.50 59 656
σ Mean Min Max
Figure 4: Result of simulation I & II.
Although the simulations are simplified, they
reflect the real situation we have met in the factory.
It is not difficult to extend the simulation with more
machines, wafer lots, and stages. We can use
different numbers of r
2
together, e.g., r
2
, r
2
r
2
, or
r
2
r
2
r
2
r
2
,…, for the task patterns to represent different
process time of different photolithography stages.
6 CONCLUSION
To provide the solution to the issue of dedicated
machine constraint, the proposed Load Balancing
(LB) scheduling approach has been presented. Along
with providing the LB scheduling approach to the
dedicated machine constraint, we also presented a
novel model--the representation and manipulation
method for the task patterns. The simulations also
showed that our proposed LB scheduling approach
was better than the LS method. The advantage of LB
is that we could easily schedule the wafer lots by
simple calculation on a two-dimensional matrix.
Moreover, the matrix architecture is easy for
practicing other semiconductor manufacturing
problems in the area with a similar constraint.
ACKNOWLEDGEMENTS
This research was supported in part by the Ministry
of Education under grant EX-91-E-FA06-4-4 and
the National Science Council under grant NSC-94-
2213-E-194-010 and NSC-92-2917-I-194-005. This
research was also partially supported by the U.S.
National Science Foundation grant No. IIS-0326387.
One of us, A. Shr, is grateful to Ms. Victoria Tangi
for English proof-reading.
REFERENCE
Arisha, A. and Young, P., 2004 Intelligent Simulation-
based Lot Scheduling of Photolithography Toolsets in
a Wafer Fabrication Facility. 2004 Winter Simulation
Conference, pp. 1935-1942.
Chern, C. and Liu, Y., 2003. Family-Based Scheduling
Rules of a Sequence-Dependent Wafer Fabrication
System. In IEEE Transactions on Semiconductor
Manufacturing, Vol. 16, No. 1, pp. 15-25.
Hildum, D., 1994. Flexibility in a Knowledge-based
System for Solving Dynamic Resource-Constrained
Scheduling Problem. Umass CMPSCI Technical
Report UM-CS-1994-77, University of Massachusetts,
Amherst.
Kumar, P.R., 1993. Re-entrant Lines. In Queuing Systems:
Theory and Applications, Special Issue on Queuing
Networks, Vol. 13, Nos. 1-3, pp. 87-110.
Kumar, P.R., 1994. Scheduling Manufacturing Systems of
Re-Entrant Lines. Stochastic Modeling and Analysis of
Manufacturing Systems, David D. Yao (ed.), Springer-
Verlag, New York, pp. 325-360.
Kumar, S. and Kumar, P.R., 2001. Queuing Network
Models in the Design and Analysis of Semiconductor
Wafer Fabs. In IEEE Transactions on Robotics and
Automation, Vol. 17, No. 5, pp. 548-561.
Lu, S.H. and Kumar, P.R., 1991. Distributed Scheduling
Based on Due Dates and Buffer Priorities. In IEEE
Transactions on Automatic Control, Vol. 36, No. 12,
pp. 1406-1416.
Mönch, L., et al., 2001. Simulation-Based Solution of
Load-Balancing Problems in the Photolithography
Area of a Semiconductor Wafer Fabrication Facility.
2001 Winter Simulation Conference, pp. 1170-1177.
Shen, Y. and Leachman, R.C., 2003. Stochastic Wafer
Fabrication Scheduling. In IEEE Transactions on
Semiconductor Manufacturing, Vol. 16, No. 1, pp. 2-
14 .
Wein, L.M., 1998. Scheduling Semiconductor Wafer
Fabrication. In IEEE Transactions on Semiconductor
Manufacturing, Vol. 1, No. 3, pp. 115-130.
Zhou, M. and Jeng, M.D., 1998. Modeling, Analysis,
Simulation, Scheduling, and Control of Semiconductor
Manufacturing System: A Petri Net Approach. In
IEEE Transactions on Semiconductor Manufacturing,
Vol. 11, No. 3, pp. 333-357.
A LOAD BALANCING SCHEDULING APPROACH FOR DEDICATED MACHINE CONSTRAINT
175
