
INTELLIGENT TUTORING SYSTEM: A MODEL FOR
STUDENT TRACKING
Francesco Colace, Massimo De Santo, Marcello Iacone
DIIIE-Università degli Studi di Salerno
Via Ponte Don Melillo, 1 84084 Fisciano (Sa)
Keywords: E-Learning, Student Model, Metadata, Adapted Learning path.
Abstract: Thanks to the technological improvements of recent years, distance education today represents a real and
effective tool for integrate and support the traditional formative processes. In literature it is widely
recognized that an important component of this success is related with the ability “to customize” the
learning process for the specific needs of a given learner. This ability is still far to have been reached and
there is a lot of interest in investigating new approaches and tools to adapt the formative process on the
specific individual needs. In this paper we present and discuss a model to capture information about learning
style and capabilities of students; this information is successively used to select the most suitable learning
objects and to arrange them in “adapted” learning paths.
1 INTRODUCTION
In the last years, distance learning is becoming one
of the most interesting topics in scientific literature
and researchers are starting to take a real interest in
the design of value-added services. In particular, E-
Learning environment should not only be limited to
transfer the content of the didactic units to the
student but also to support a new concept of didactic
whose final objective is to increase the contribution
of the traditional teaching thanks to Information and
Communication Technology. Among these services,
one of the most interesting is the student activities
tracking service. In fact the main criticism to E-
Learning approach is the lack of direct contact
between teachers and students: by tracking services
teachers can track and support students in their
learning process. However, new E-Learning
platforms can collect and manage a large size of data
concerning the student’s learning process. But this
very impressive number of information can bewilder
teachers that don’t use fully them. Usually a teacher
uses few information: the students’ results at the
final or end-unit tests. Obviously, this information
can not explain all the aspects of student’s
knowledge process and teachers can not support
effectively them. In this context, a set of learning
parameters has to be selected and used for tracking
operation. In literature, many papers deal with this
argument and offer several models whose target is
the identification of these parameters in E-Learning
process (Zaitseva, 2003). Some of them are based on
the tracking of the student knowledge by using the
formalism of the graphs where the nodes estimate
the student’s knowledge (Specht, 1998). Other
approaches analyze the actions of the student during
his learning process furnishing a detailed report to
the tutor (Greer, 1997)(Thomson, 1996). An
interesting approach is proposed in (Shang, 2001).
This paper describes a model that builds the best
students’ learning path starting from the analysis of
some features outlining the main pedagogical
characteristics. This approach is student-centred and
students’ parameters are selected according to three
factors:
Test performance: this parameter gives the most
direct information about the student’s knowledge.
Time performance: the time spent by student
attending the various modules.
Reviewed topics: A topic’s review score records
how many times the student has returned to review
the topic. It is based on how many times the topic is
reviewed and how much of the material is viewed
each time.
The above factors, described by an opportune
mathematical model, indicates to teachers the
learning level achieved by students. By analyzing
these indexes, moreover, it is possible to establish if
students may attend the next subject of the course.
Starting from this approach in this paper we propose
110
Colace F., De Santo M. and Iacone M. (2006).
INTELLIGENT TUTORING SYSTEM: A MODEL FOR STUDENT TRACKING.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - HCI, pages 110-115
DOI: 10.5220/0002457201100115
Copyright
c
SciTePress

a model for tracking student’s activities during his
learning process. We have selected some indexes
able to describe the student attitude during the
learning process. In particular this approach updates
the student’s profile (described according to IMS
LIP standard) in order to adapt its learning path
(Colace, 2003). This paper is organized in this way:
the problem of student’s tracking is presented in
section two. In section three the tracking indexes are
introduced and the mathematical model of the
student obtained with their combination is described.
In section four the rules used to build the best
learning path are analyzed. In section five some
experimental results are showed.
2 THE TRACKING PROBLEM
In this section we describe an approach for tracking
the student‘s preparation during his learning activity.
To this aim, it is necessary to design a method for
tracking the student in a more useful and concrete
way in order to help the docent in an effective
evaluation. The proposed approach takes into
account the difficulties that the student meets when
he faces a didactic unit and furnishes to each student
the most adapted didactic unit to his actual
knowledge. Our approach is able to watch how
much he is learning, which topics are very difficult
for him and how it is possible to give to him the
appropriate feedbacks. From this point of view, the
system helps the docent by furnishing the best
pedagogical contribution for the learning process of
each student. How it is possible to choose the best
learning path for each student? It is supposed to
know how time the student spends when he faces a
Learning Object (t
k
) and the mark he obtains in the
final test (v
k
). The time student t
k
is matched with a
reference learning time that the docent has a priori
assigned, t
r
k
., for the k-th Learning Object. This
matching is made by using an appropriate rational
function G
t
. The goal of G
t
is, by setting opportunely
its parameters, to give the right weight if the student
has spent a lot of or little time in the making use of a
lesson. Moreover, the mark student v
k
is matched
with the reference mark v
r
k
. the docent has a priori
assigned for that Learning Object by using an
appropriate rational function G
v
. In this way, if the
student has obtained a good mark, his profile is
updated and the successive adapted didactic unit is
located, otherwise a unit with the same content but
less difficult is chosen for him (also in this case it is
necessary to update the student profile). The scheme
of the process is showed in fig. 1. In the next sub-
sections we will describe in details the various
phases of our approach.
Selection
of
Learning
Object
Study of
Learning
Object
End
Module
Test
User
Profile
Updating
Start
Course
End
Course
Score
k
Score
LO
k+1
Selection
of
Learning
Object
Study of
Learning
Object
End
Module
Test
User
Profile
Updating
Start
Course
End
Course
Score
k
Score
LO
k+1
Figure 1: Reference model of the proposed Approach.
2.1 Selection of Learning Object
The opportunity of better defining a resource by
using its didactic and pedagogical characteristics
suggests representing it with a model. The idea is to
generate a “digest” of learning objects. Our aim is to
better qualify the resource, making it clear to the
software module, which interacts with the contents,
the knowledge domain to which it belongs and its
more peculiar characteristics. At the same time, a
model allows to quantify the resource making it
possible to establish a relation among metadata by
using appropriate metrics. The objective
quantification makes it possible for an intelligent
software tool to propose the contents that are
suitable to the student needs. We have therefore
implemented a software module able to model the
single described training resource through a string
vector whose components summarize specific
resource features. This representative vector is so
defined:
Didactic Resource ={Typology, Ontology, Pedagogical
educational properties, Technical requisites, Rights}
Each component of this vector is still a string vector,
and represents a particular aspect of the resource and
gathers the most important information obtained by
combining standard description fields. We have
chosen to use a vector since this structure better
organizes the information associated with the
resource allowing its easier retrieval. It is clear that
the possibility of presenting this vector
representative of learning object semantic content to
an intelligent software module, which is able to
semi-automatically infer decisions concerning the
training contents utilization, as an Intelligent
Tutoring System is able to do, improves and
optimizes its performances in the retrieval process.
We are going to explain in detail the descriptive
vector components:
{Typology}: this category gives a global and general
vision of the resource. This vector contains all useful
information for classifying the learning object.
{Ontology}: this vector has to explain in which
didactic context the resource can be inserted. This
component has to provide information in order to
INTELLIGENT TUTORING SYSTEM: A MODEL FOR STUDENT TRACKING
111

contextualize the training resource in a well defined
knowledge domain. Thanks to this vector, it will be
possible to associate each resource with other
training resources that belong to established
knowledge domains allowing in this way the
organization of training paths. Besides, this type of
representation seems to be particularly suitable for
locating and recovering the resource itself within the
domain.
{Pedagogical Educational Properties}: this vector,
describing the pedagogical and educational
characteristics, defines the resource. It is so possible
to know the interactivity level of the resource with
the user, its semantic density, and in general to
pedagogically define it.
{Technical requisites}: this vector has to describe
the technical requisites necessary to the correct
utilization of the resource. In particular, it is engaged
in defining what its technological format is, what
operating system makes it work, and what software
is necessary for its correct utilization. In addition, it
makes it possible to find the actual location of the
resource.
{Rights}: This vector describes the billing modes
and the costs associated with the resource.
Every component matches with the respective
descriptive IMS standard field. In this way we can
work with a well defined set of standard
information, which is also the most meaningful, and
we can use all descriptive fields when more detailed
information is needed.
The choice of the best training path obviously
involves the choice of the learning objects more
suitable to the student preferences. The resource,
using ontology standard description, can be chosen
taking into account the pedagogical context in which
the user attends the lesson. From the point of view of
size, light resources (in byte) should be preferred in
case of non high-quality Internet connections.
Another aspect to be considered is related to the time
that the user can dedicate to the lesson. The system
must therefore offer resources whose learning time
estimated by the teacher should not overcome the
time that the user would like to spend attending the
lesson. Our module has to acquire the following
information from the standard descriptive fields of
the user profile: Interactivity level preferred by the
student in the resource, student learning level, time
dedicated by the student to the lesson, connection
type usually used by the user, preferred user
language. In this way, we can create a vector similar
to the learning object digest vector introduced in the
previous paragraph. The information contained in
the fields of this vector will be interpreted,
manipulated and kept in a special structure, in this
case a numerical vector, which represents, from a
numerical point of view, the resource and the user
profile. The structures are so defined:
User = {Difficulty
u
; Interactivity
u
;
Size
u
;
Time
u
}
Training resource = {Difficulty
r
;
Interactivity
r
; Size
r
; Time
r
}
The Difficulty field in the vector User is closely
related to the results obtained by the user during the
courses and contains a numerical value representing
the arithmetical mean of the results obtained until
the present time. Our software module therefore uses
this numerical information to create a range of
values. The Difficulty field in the vectors’ Training
resource is obtained from the field of Pedagogical
Educational Properties of vectors that describe the
learning object. In this case this information is
manipulated and arranged in order to obtain a value
in the range of 0-10. As previously said, the vector
Pedagogical Educational Properties contains
numbers and strings related to the learning object
description. The first step is to transform each string
content in a numerical value in the range 0-10.
Obviously we manipulate only the information of
interest (for example the field description is not
useful). At the end of this phase we obtain the
difficulty field number as a weighted average of all
values. In particular, we give a greater weight to
features as difficulty and semantic density. The
Interactivity Level field contains the interactivity
level preferred by the student within a training
resource. Our module divides the interactivity level
in L
max
sub-levels (from very low level to very high
level) and assigns a numerical value (from 1 to 10)
to each level. Also in this case the system retrieves
information from the description of learning object
through the most appropriate fields of {Pedagogical
Educational Properties} (for example interactivity,
interactivity level and so on) and {technical
requisites} (for example format: in this case we give
greater values for format as video, flash animation
and lower values for format as doc, pdf, ppt and so
on). The Size field describes the connection capacity
generally used by the student. For the learning object
the information is obtained by manipulating the field
Size of the vector {Technical requisites}. The
software module executes the same operation for the
Typical Learning Time features that describes the
time usually spent by the user in attending the
lesson. In order to obtain the best correspondence
between User Resource and Training Resource, we
have calculated a correspondence index (Ind) by
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
112

using the following formula, where α, β, χ, δ are
integer values:
Ind = α|Difficulty
u
-Difficulty
r
|+β|Interactivity
u
-
Interactivity
r
|+ χ|Size
u
-Size
r
|+ δ|Time
u
-Time
r
|
As can be deduced, all the single contributions are
taken into account, opportunely evaluated by the
weight α, β, χ, δ, provided by the single
components. The α value is higher than all the
others in order to emphasize the difficulty of each
contribution since it is not appropriate to offer
training contents with a difficulty level greater than
the student profile provides. The formula gives back
value zero when the observed resource exactly
presents the same values as the user resource
obtained from his profile. The more the index values
are distant from the value zero, the more the
resource observed is distant from that student needs.
Our tool builds a lesson using a fundamental content
(the most suitable content for the user), adds some
additional contents and a final test. After the
evaluation of the final test, the user profile and the
course structure is updated.
2.2 Study of Learning Object
In this phase the student time t
k
of a single learning
object is evaluated. Eventually, the student can ask
to repeat the same lesson before he makes the test. In
this case, the following function is evaluated:
1
() ]0,1] 1,2,3,...
1(1)
k
Ti i
ai
=∈=
+−
where i indicates the number of items the student
faces the same learning object and 0<a<1 is a real
parameter. The function T
k
(i) gives to the student a
decreasing score little by little he makes use of the
same learning object.
2.3 End Module Test
In this phase the learning state of the student is
evaluated with a mark v
k
. The following parameter is
evaluated:
,
kk
k k k max
k
max
Lv
Qv vL
d
L
⎡⎤
=∈
⎢⎥
⎢⎥
⎣⎦
where L
k
indicates the difficulty level of the k-th
Learning Object, fixed a priori by the docent; d
k
indicates the actual training state of the student
about the k-th Learning Object. It is supposed that L
k
and d
k
belong to the same range [1:L
max
]. Q
k
provides detailed information about the punctual
performance of the student. The term L
k
/d
k
expresses
an adapting factor between the student state and the
selected learning object. Therefore Q
k
relates the
adapting factor to the student mark and describes
how much v
k
is reliable. For example, if a student
obtains v
k
=9, we could suddenly say he his clever;
but if we find that this mark has been reached with
L
k
=2 and d
k
=7, we can realize the proposed learning
object has not been appropriate and so v
k
does not
represent the real student’s level of knowledge.
Once Q
k
is known, the following amount can be
calculated:
1
1
1
() ,
1
1
k
pk max
k
max
q
q
Q
SQ L
L
Q
k
−
=
⎡⎤
=∈
⎢⎥
⎢⎥
⎣⎦
−
∑
that puts in relationship the student evaluation (Q
k
)
to his previous mean performance.
2.4 User Profile Updating
At the end of the test, in any case, the student profile
is updated and a report on his activity is provided. At
this point, the following evaluation function of the
student on all his activity concerning the k-th
Learning Object is considered:
10
( ) (1 )(1 log ( ( )))
v
kk pk
t
G
Score T i S Q
G
⎛⎞
=μ + −μ +
⎜⎟
⎝⎠
where:
22
2
2
()
1
()
r
kk x
t
r
x
kk
tt t
GN
t
tt
N
−−
=+ +
−+
with:
lim 1
r
kk
t
tt
G
→
=
lim 2
k
t
t
GN
→∞
=+
is the matching function between the time student t
k
and the learning time t
r
k
. fixed by the docent.
Moreover t
x
is a time parameter (also fixed by the
docent) such that in the range [t
r
k
. - t
x
, t
r
k
. + t
x
] the
student has spent a reasonable time for the lesson. If
t
k
= t
r
k
., the G
t
function has value 1 and the student is
not penalized. Otherwise, if t
k
is very far from t
r
k
.,
Score
k
decreases. The parameter N fixes how much
the student is penalised (fig. 2). Moreover:
[]
1, 1
r
kk
v
r
kk
vv
G
vv
−
=∈−
+
with:
lim 0
r
kk
v
vv
G
→
=
,
lim 1
k
v
v
G
→∞
=
,
0
lim 1
k
v
v
G
→
=−
is the matching function between the student mark v
k
and the minimum mark fixed by the docent. The
INTELLIGENT TUTORING SYSTEM: A MODEL FOR STUDENT TRACKING
113

threshold v
r
k
. is proportional to the difficulty of the
argument:
]0,1]
r
kk
vbL b=∈
In this way, if an argument is very difficult (L
k
high),
it is reasonable to raise the threshold of the test. The
G
v
function allows seeing very easily if the student
mark v
k
is satisfactory respect to the reference mark
v
r
k
.. The G
v
function is very simple. In fact, it is
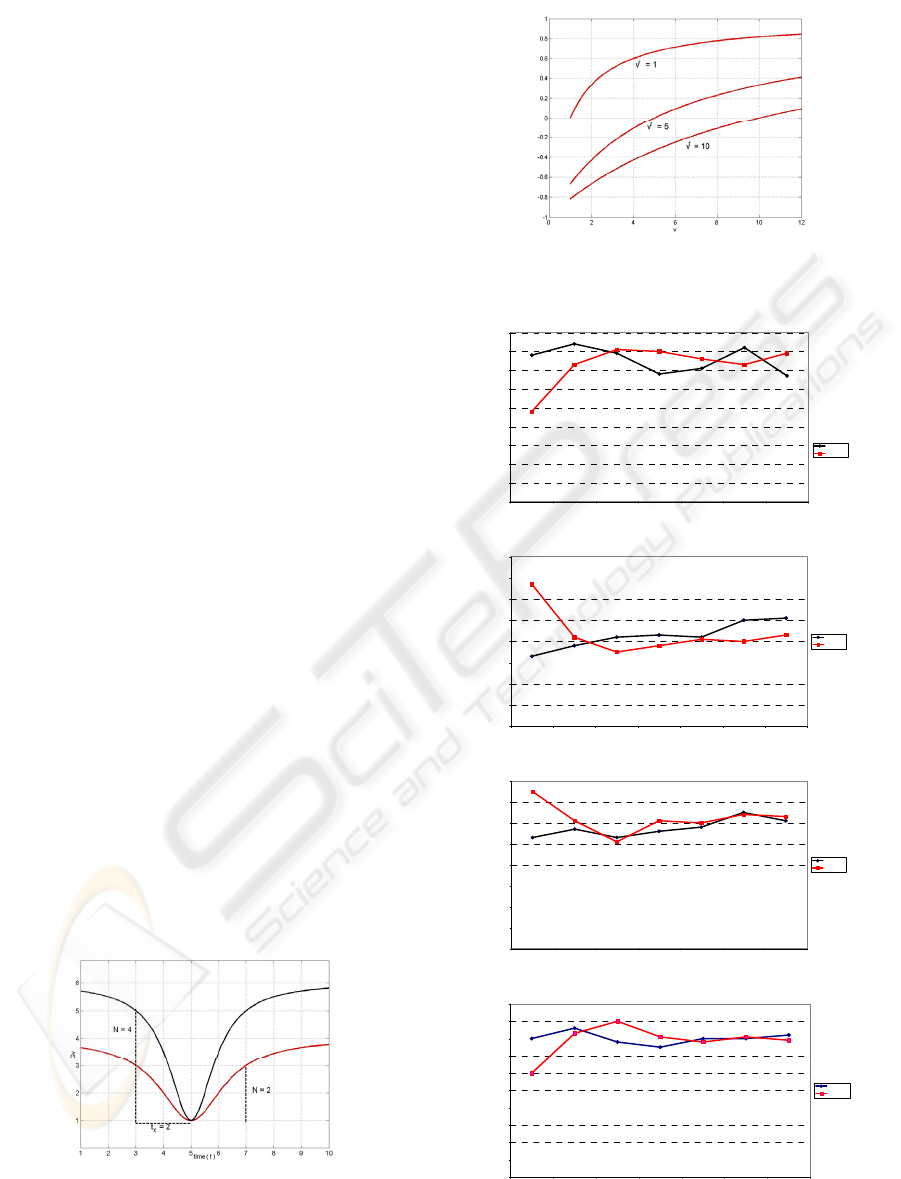
useful to see only his sign (see fig. 3):
0
0
0
r
kk v
r
kk v
r
kk v
vv G
vv G
vv G
⎧
>⇒ >
⎪
<⇒ <
⎨
⎪
=⇒ =
⎩
In (4) the real positive parameter μ makes the weight
average between the first term (T
k
(i) G
v
/G
t
) that
takes into account the actual performance of the
student and the second term, 1+Log
10
(S
p
(Q
k
)), that
takes into account the historic performance of the
student. Finally, the function Score
k
is:
22
2
2
1
1(1)
()
1
()
r
kk
r
kk
k
r
kk x
r
x
kk
vv
vv
Score
ai
tt t
N
t
tt
N
⎛⎞
⎜⎟
−
⎜⎟
⎜⎟
+
=μ +
⎜⎟
+−
−−
⎜⎟
++
⎜⎟
⎜⎟
−+
⎜⎟
⎝⎠
10
1
1
(1 ) 1 log
1
1
k
k
k
k
q
q
q
q
L
v
d
L
v
kd
−
=
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
+−μ +
⎜⎟
⎜⎟
⎜⎟
⎜⎟
−
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
[
]
0, 2∈
If v
k
<v
r
k
. a new Learning Object, defined by L
k
= L
k
- 1,
is located so that an easier argument is furnished to
the student. The maximum value of Score
k
is
obtained with the highest mark and for t
k
=t
r
k
.. Once
all Score
k
are evaluated, the global evaluation index
of the student about the didactic unit is:
1
1
M
i
i
Score Score
M
=
=
∑
if it is supposed that the learning path is formed by
M Learning Objects. Otherwise
1
M
i
i
i
Score Score
=
=γ
∑
with 0<γ<1 (for example γ=0.9). In the first formula
each Score
i
has the same weight in the student
evaluation relevant to the overall unit didactic while,
in the second one, the student score of the latest
Learning Object has a major weight respect to the
previous and so on.
3 EXPERIMENTAL RESULTS
In our experimentation we have considered the
course of “Introduction to Computer Science” at the
Foreign Literature and Language Faculty of the
University of Salerno. This course is composed by
seven modules: Introduction to PC Architecture,
Introduction to Operative System, Microsoft Word,
Microsoft Excel, Microsoft Access, Microsoft Power
Point, and Computer Network. Every module has
some sub-modules. We have created a synthetic
dataset composed by five hundred descriptions of
learning objects (related to the various modules)
according to the model previously described. All the
values needed by features of the model are simulated
through a Montecarlo method. Obviously, learning
objects belong to various modules according to the
ontology model described by the teacher. At the
same time the teacher has described the profile of
some typical students (clever, average, poor). At this
point we have simulated a course; in particular at the
end of every learning object we have simulated a
test. The results of the students are obtained through
a Montecarlo method approach based on their
profiles. In fig. 4 we can see the obtained results. In
particular, the showed values of students’ and
contents’ descriptions are the average of contents
and students in every module. The first content is
associated to the student in a random way. In the
figure we can see as our approach is able to follow
the user profile offering the more fit contents to the
students. Our approach has been simulated on about
thirty user profiles and the obtained results confirm
that the average difference between students’ and
contents’ descriptions is less than 0,8 (starting by a
first random content). Our approach is able to
furnish contents that are, in a much closed range, in
comparison with the student description.
4 CONCLUSION
In this paper we have showed a student tracking
model based on the definition of a set of features
related to the concepts, skills and attitudes the
student is expected to assimilate by the end of a unit.
Each feature is represented by means of appropriate
mathematical functions, which are combined in a
mathematical model devised to facilitate the course
characterization and comparison and to provide
support for diagnostics. In this paper we have
showed the design and implementation of a
software module for deducing the representative
“vector” of a given student starting from the
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
114
standard description of various resources (student
profiles, content descriptions and so on). We have
discussed some experimental results in using the
quoted vectors to find the most suitable set of
contents for each student profile, confirming the
effectiveness of the here proposed student model.
In the future we will extend this approach to a real
classroom in order to test his real effectiveness.
REFERENCES
Zaitseva L., Boule C., "Student Models in Computer-
Based Education", Proceedings of the third IEEE
International Conference on Advanced Learning
Technologies, 2003.
Specht M., Oppermann R., “ATS - Adaptive Teaching
System a WWW-based ITS”, Workshop Adaptivität
und Benutzermodellierung in Interaktiven
Softwaresystemen, 1998
Greer J. E., Philip T., “Guided Navigation Through
Hyperspace ”, Workshop Intelligent Educational
Systems on the Word Wide Web, 1997.
Thomson J. R., Cooke J., Greer J. E., “The MicroWeb
toolkit: Bringing the WWW to the classroom”,
Proceedings of WebNet 96 - World Conference of the
Web Society San Francisco, 1996.
Yi Shang, Hongchi Shi, Su-Shing Chen, “An Intelligent
Distributed Environment for Active Learning”,
Journal on Educational Resources in Computing
(JERIC), 1, 4, 2001.
Kent, J.J., Schuerhoff, M., “Some thoughts about a
metadata management system”, Scientific and
Statistical Database Management, Proceedings Ninth
International Conference on, Volume: 1, 1997
Colace, F.; De Santo, M.; Molinara, M.; Percannella, G.,
“An automatic learning contents selector based on
metadata standards”, Proceedings of ITRE 2003
IEEE International Conference, 2003
FIGURES
Figure 2: Two examples of Gt function with same value of
tx , different values of N and trk.=5.
Figure 3: Three examples of Gv function with three
different values of vr.
Student A
0
1
2
3
4
5
6
7
8
9
1234567
Modules
Student and Modules Description
Student
Contents
Student B
0
1
2
3
4
5
6
7
8
1234567
Modules
Student and Content Description
Student
Contents
Student C
0
1
2
3
4
5
6
7
8
1234567
Modules
Student and Content Description
Student
Contents
Student D
0
1
2
3
4
5
6
7
8
9
10
1234567
Modules
Student and Modules Description
Student
Contents
Figure 4: Examples of students’ tracking.
INTELLIGENT TUTORING SYSTEM: A MODEL FOR STUDENT TRACKING
115
