FACE RECOGNITION FROM SKETCHES USING ADVANCED

CORRELATION FILTERS USING HYBRID EIGENANALYSIS

FOR FACE SYNTHESIS

Yung-hui Li

Language Technology Institute, Carnegie Mellon Universty

Marios Savvides and Vijayakumar Bhagavatula

Department of Electrical and Computer Engineering, Carnegie Mellon University

Keywords: Face from sketch synthesis, face recognition, eigenface, advanced correlation filters, OTSDF.

Abstract: Most face recognition systems focus on photo-based (or video) face recognition, but there are many

law-enforcement applications where a police sketch artist composes a face sketch of the criminal and that is

used by the officers to look for the criminal. Currently state-of-the-art research approach transforms all test

face images into sketches then perform recognition in the sketch domain using the sketch composite,

however there is one flaw in such approach which hinders it from being deployed fully automatic in the

field, due to the fact that generating a sketch image from a surveillance footage will vary greatly due to

illumination variations of the face in the footage under different lighting conditions. This will result

imprecise sketches for real time recognition. In our approach we propose the opposite which is a better

approach; we propose to generate a realistic face image from the composite sketch using a Hybrid subspace

method and then build an illumination tolerant correlation filter which can recognize the person under

different illumination variations. We show experimental results on our approach on the CMU PIE (Pose

Illumination and Expression) database on the effectiveness of our novel approach.

1 INTRODUCTION

Face recognition has attracted much attention in

recent years and many different methods have been

proposed (Zhao, 2000). However, most of the

proposed methods focus on the problem where both

training and testing images are face images. In

practical law-enforcement scenarios, we may

encounter the situation where a police-sketch of a

suspects face image is available. For example, in

many criminal investigations there are usually one or

two human witnesses that have caught a glimpse of

the criminal or terrorist suspects and the police and

government authorities must use this vital

information as a means to catch these suspects. In

such cases, typically a professional police sketch

artist will work and co-operate with the witnesses to

develop and synthesize a police sketch of the suspect.

This sketch is then distributed among police officers

in efforts to look for the suspects at ports of entry or

other locations.

Figure 1: Examples of face and their sketch images.

In this case, we only have the drawing or sketch

image of the subject to work with. In this paper we

propose a novel approach of trying to retrieve or

synthesize a real face image that can be used by

law-enforcement personnel and more importantly by

an automatic face recognition system.

Li Y., Savvides M. and Bhagavatula V. (2006).

FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID EIGENANALYSIS FOR FACE SYNTHESIS.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - HCI, pages 11-18

DOI: 10.5220/0002457400110018

 SciTePress

Figure 1 shows a couple of examples of face

images and their corresponding sketch images. One

can easily observe that face and sketch have

different modalities. In general, sketch images are

more focused on the prominent shape parts of face

(eyes, nose, mouth). In short, information in sketch

images is much fewer than information in face

images. Therefore, performing recognition based on

sketch images is harder than doing it on face images.

1.1 Previous Work

Wang & Tang (Tang, 2002, 2003, 2004, 2005) have

tackled this approach in a different way. They divide

the task into two phases: At the first phase, they

transform all the face images in their database into

sketch images using various approaches, for

example, eigenspace (Tang, 2004) and LLE (Tang,

2005). This phase can be called “synthesis phase”.

Second, they perform all the recognition tasks on

sketch image domain using a different approach, for

(Hybrid Space)

Hybrid

Eigenvectors

Pseudo-eigensketch is the lower half of the hybrid

eigenvectors

Face images

Sketch images

Figure 2: Illustration of experimental procedure during training phase.

ICEIS 2006 - HUMAN-COMPUTER INTERACTION

example, distance metric (Tang, 2004), Bayesian,

LDA, PCA and KNDA (Tang, 2005).

2 PROPOSED METHOD

Due to the observation that information is fewer in

sketch space, we propose a new method to attach

face-sketch recognition problem which is exactly the

opposite way to the method described in (Tang,

2002, 2003, 2004, 2005). We propose a novel

algorithm to reconstruct face image from its sketch

counterpart, and by means of a powerful pattern

recognition technique, as shown in (Savvides, 2002,

2004, 2005), we can perform recognition in face

subspace even if our database for matching only

have candidate images taken in very bad

illumination condition. More importantly, our

proposed approach can be implemented into a fully

automatic system which can be easily deployed in

real life scenario.

2.1 Training Phase

Our problem in training phase can be stated as

following: Given a database consisted of face

images from many people and corresponding sketch

images, how can we derive a set of feature that can

catch the intrinsic mapping function between face

and sketch images. How do we practically calculate

those features? How can we use those features to do

the pattern matching task when there’s a new sketch

image coming in?

The state-of-the-art technique in face recognition

gives us an implication for this problem. It has been

shown that performing eigen-analysis over face

images, as stated in (Turk, 1991), can capture the

principle components in a set of face images, and

those principle components (eigenfaces) can be very

Figure 3: The comparison of eigenfaces derived from three difference spaces. The first row is the eigenfaces derived from

hybrid space. The second row is the eigenfaces derived from face images only. The third row is the eigensketch derived

from sketch images only. Note that while the pseudo-eigenface and pseudo-eigensketch images are highly correlated

among the images at first row, the eigenfaces in second row are not correlated to the eigensketch in third row. Hence,

calculating eigenface and eigensketch independently will not keep the corresponding information between each other,

while calculating eigenface in hybrid space will

FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID

EIGENANALYSIS FOR FACE SYNTHESIS

helpful later when we are interested in

reconstructing new face images.

If we decide to use eigenface approach to attack

this problem, the next question is: how are we going

to utilize eigenface technique to derive features

across both face and sketch subspace? Face and

sketch images are very different, so if we perform

eigen-analysis over face and sketch subspace

independently and get eigenface and eigensketches

respectively, and substitute the projection

coefficients from one subspace to another, basically

we are assuming the transformation between face

and sketch are linear, as stated in (Tang, 2003). But

in practice, since sketch images are drawn by artists,

it is not a linear transformation, thus we propose a

solution based on performing eigen-analysis in

hybrid subspace. By hybrid subspace, we are saying

that we create a subspace by concatenating face and

sketch images. After creating data in such

face-sketch hybrid subspace, we perform

eigen-analysis on this subspace and get the

eigenvector matrix in this hybrid subspace. The

basic flow of training is described in section 3.2,

also shown in Figure 2.

Note there is an interesting fact that if we

calculate eigenface and eigensketch independently

from our database, the resulting eigenfaces are not

correlated to resulting eigensketches, as shown in

Figure 3. But by performing eigen-analysis on

hybrid subspace, we can clearly see that the upper

half of each eigenvector is highly correlated with the

lower half of it, which means our proposed method

can capture the nonlinear mapping function between

face and sketch images.

After we get eigenvector matrix in hybrid

subspace, we retrieve the eigensketch matrix by only

keeping the lower half of each eigenvector of hybrid

subspace. Note that these eigensketch vectors we get

with this method may not be orthonormal to each

other since the orthogonality has been destroyed by

cropping out the upper half of the vector. So we

will call them “pseudo-eigensketches”.

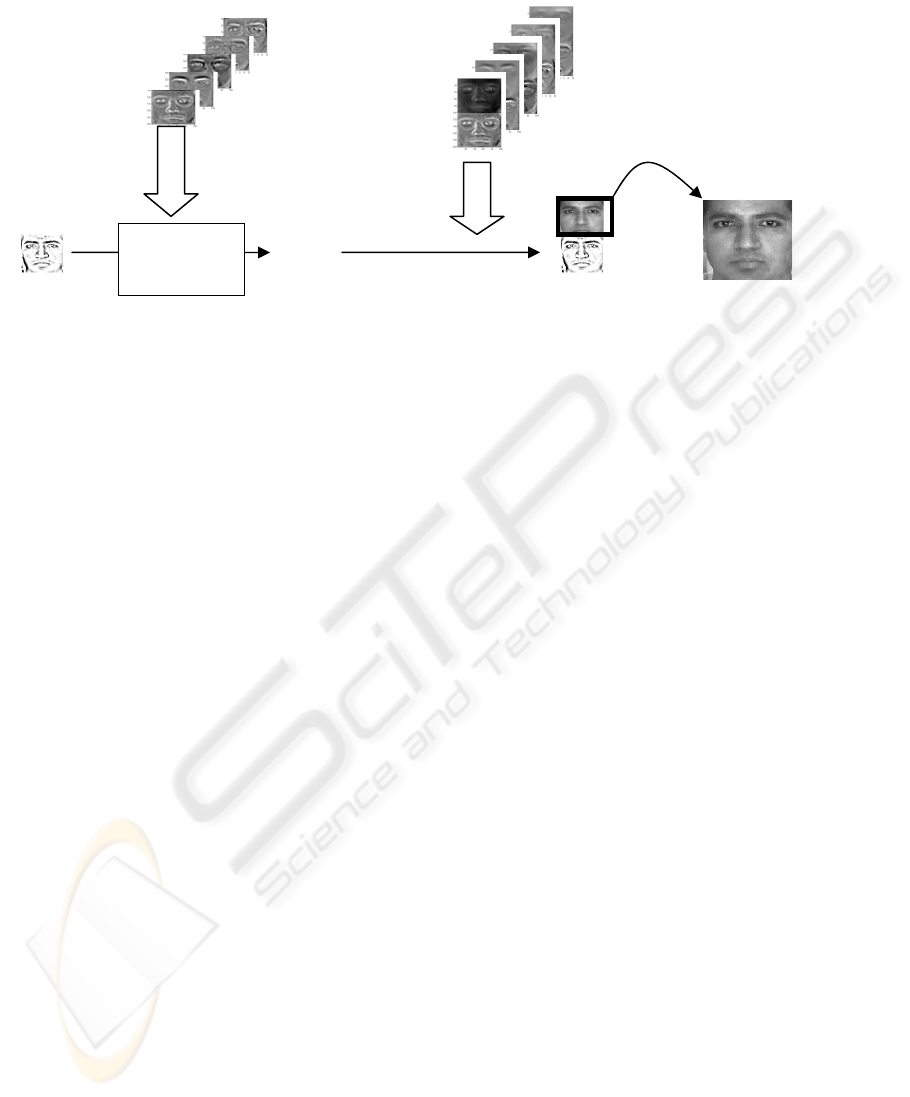
2.2 Reconstruction Phase

At testing phase, our job can be divided in two

stages: reconstruction phase and recognition phase.

At reconstruction phase, when a new sketch

image comes in, our goal is to reconstruct the

original face image corresponding to this sketch that

can be used by police officers to look for the person

and this image can also be fed into the automatic

face recognition system to look for the person in

real-time systems.

Since we already have the “pseudo-eigensketch”

computed from training phase, we follow the typical

eigenface approach to reconstruct face. First, we

compute the projection coefficients of this sketch

over pseudo-eigensketch. Since our

“pseudo-eigensketch” is not a set of orthonormal

basis, we use pseudo-inverse least squares fitting

technique to compute the projection coefficients

which produce the sketch with the least-squared

error. After we have those coefficients, we

reconstruct the facie image in hybrid subspace by

using the computed least-square projection sketch

coefficients on the pseudo-eigenfaces in hybrid

subspace.

Probe sketch

Projection

coefficient

Pseudo-eigens

ketch

Hybrid subspace

Eigenvector

Reconstructed

image in hybrid

subspace

Reconstructed face

image

Pseudo-

inverse

Figure 4: Illustration of experimental procedure during reconstruction phase.

ICEIS 2006 - HUMAN-COMPUTER INTERACTION

()

(

) ()

()

Cdevstd

CmeanC

CPCE

max −

The whole reconstruction process is illustrated in

Figure 4. Some example of pairs of original face and

reconstructed face are shown in Figure 5.

One can also notice that the reconstructed

images are a little brighter than the original ones,

this is due to some ambiguity as the sketch images

completely ignore So, if we perform recognition

with distance-based metric, like one nearest

neighbour (1NN), the distance between original

image and reconstructed ones will be very large.

Therefore, we have to use a robust pattern

recognition method which is able to handle the

illumination variation and still be able to achieve a

good recognition result. To achieve this we choose

advanced correlation filter as our recognition

approach.

2.3 Recognition Phase – Using

Advanced Correlation Filters

Advanced correlation filters (Kumar, 1992) are

advanced template-based classifiers that when

correlated with an image result in a correlation

plane. The correlation plane C measures the

correlation between the filter and the image.

Correlation of a class-specific filter with authentic

and impostor data yield very different correlation

planes. Figure 6 demonstrates this difference. These

advanced correlation filters optimize specific criteria

to obtain sharp correlation peak outputs as shown

below; this is very different from matched filters or

normalized correlation approaches which are more

common in the literature.

To quantify the difference between the two types

of correlation planes, we define a measure of

recognition called Peak to Correlation Energy

(PCE). This is a measure the sharpness of the largest

peak in the correlation output with respect to the rest

of the correlation plane.

(1)

The Minimum Average Correlation Energy

(MACE) Filter (Mahalanobis, 1987) is designed to

minimize the average energy E in the correlation

plane or Average Correlation Energy (ACE). In

the filter design h we also constrain the value of the

correlation peak at the origin to be set to 1.

Assuming that we have a matrix X which contains

the 2D Fourier transforms of training images along

the columns we can write the linear constraints as

follows:

h=u (2)

To achieve peak sharpness we must then also

minimize correlation plane energy, thus we compute

the average power spectrum of the face image which

is vectorized and placed on the diagonal of matrix D.

Our goal is to minimize E which is defined as:

DhhE

= (3)

where

denotes the conjugate transpose. The

constrained minimization of equation 2 results in the

MACE filter h

MACE.

(4)

where u is the constrained peak values (vector of

ones).

(

)

uXDXXDh

MACE

−

−+−

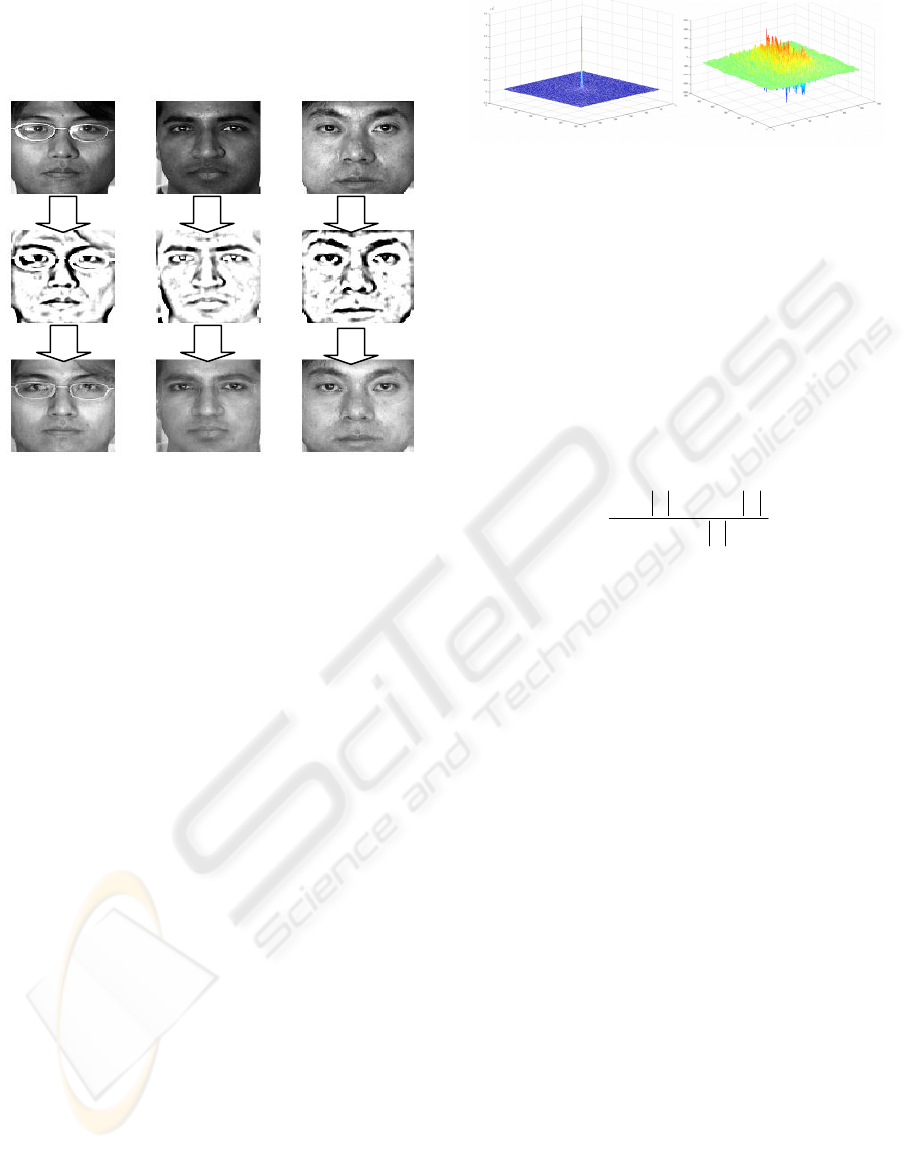
Figure 5: Examples of original face and corresponding

reconstructed face when we only have sketch images.

The images in first row are original face; the images i

second row are sketch of the face images, and the images

in third row are reconstructed face images from sketches.

Figure 6: Left: correlation plane of an authentic sample.

Right: Correlation plane of an imposter sample.

FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID

EIGENANALYSIS FOR FACE SYNTHESIS

The Unconstrained MACE (UMACE) Filter

(Mahalanobis, 1994) removes the constraint on the

peak value. By removing this constraint, we may be

able to find a better solution to the energy

minimization. Instead, we try to maximize the

average value of the peaks or Average Correlation

Height (ACH). The closed form solution to the

UMACE filter h

UMACE

= D

-1

m (5)

where m is the average of the columns of X.

We will consider generalizations of the MACE

and UMACE filters called the Optimal Tradeoff

Synthetic Discriminant Function (OTSDF) filter

(Kumar, 1994) and the Unconstrained OTSDF

(UOTSDF) filter respectively. These generalized

filters offer sharp correlation peaks and some noise

tolerance. Given a desired proportion of peak

sharpness to noise tolerance, the filter designs

OTSDF

and h

UOTSDF

are:

(6)

(7)

where T is defined as:

(8)

where C is the assumed to be white noise power

spectral density (so in this case C=I the identity

matrix). In this paper we use OTSDF (alpha=0.99)

throughout all the recognition experiments.

3 EXPERIMENTS

The database we used in our experiment is

CMU-PIE database (Sim, 2001). The PIE database

consists two datasets which we will refer to as Light

(images captured with ambient background lighting)

and NoLight(images captured without any

background lighting on). Light database contains the

pictures which were taken under sufficient

environmental lighting, so in general one can see

clear face images in all pictures in Light database.

NoLight database contains pictures taken in the

harshest illumination conditions, so the face suffers

with larger cast shadows making face recognition in

NoLight database a much harder task than in the PIE

Light database because of these harsh illumination

variations.

There are 65 people in both databases. In Light

database, each person has 22 images; in NoLight,

each person has 21 images captured under different

lighting variations. Total number of images in this

database is 2795. CMU-PIE database has following

characteristics:

z Contains both male and female faces

z Contains people from different race and

color

z Contains images of people with and

without glasses.

z Contains severe illumination variation

across images of each person, as shown in

Figure 7 and 8.

As one can imagine, due to the large variation in

gender, skin colour, the presence or absence of

eye-glasses, and illumination; this is a very

mTh

UOTSDF

1−

()

uXTXXTh

OTSDF

−

−+−

101

≤≤−+=

ααα

givenCDT

Figure 7: Examples of CMU-PIE-Light database. For each person there’re 22 images, each of which has different

orientation of illumination

Figure 8: Examples of CMU-PIE-NoLight database. For each person there’re 21 images, each of which has different

orientation of illumination

ICEIS 2006 - HUMAN-COMPUTER INTERACTION

challenging task to perform face recognition on this

database.

Since CMU-PIE database only contains face

images and not sketch images, we have to generate

corresponding sketch images for each of the face

image in database. We used one of the non-linear

sketch functions in Adobe PhotoShop® to manually

generate all corresponding sketch images for each of

the face. Examples of face and sketch images are

shown in Figure 1.

During the training phase, we selected two

images with evenly distributed illumination (i.e.

neutral frontal lighting) from every person, calculate

eigenvectors in hybrid subspace. During recognition,

we pick one sketch image, then reconstruct the face

image using algorithm described in Section 2.1.

Then from all face images of each person, we match

the reconstructed face image with all rest images (all

images except the two for training and the one for

reconstruction). The rational for doing this is to

simulate the real scenario when our system is

applied in real life where the person we are looking

for is walking under varying illumination causing

their facial appearance to vary significantly due to

lighting. The proposed method will allow us to

match the reconstructed face images with those

pictures taken from a surveillance camera. So we

believe this experiment setting will yield results

which are more strongly related with the one we

would get in real world application.

3.1 Matching Process

The procedure for training phase is illustrated in

Figure 2. Basically we can summarize it into

following steps. Given a set of face images and their

corresponding sketch images:

(1) Form a new hybrid face-sketch subspace by

appending every sketch to the end of the

corresponding face image.

(2) Perform eigen-analysis to calculate the

eigenvectors of the covariance matrix of the

face-sketch data

(3) The pseudo-eigensketches are obtained by

clipping off the upper half of eigenvectors

of the hybrid subspaces.

The procedure for reconstruction phase is

illustrated in Figure 4. Basically we can summarize

it into following steps:

(1) For each probe sketch image, we would

like to calculate the projection coefficient

when it is projected on

pseudo-eigensketch subspace. We use

least-squares fitting method to estimate

these projection coefficients given a test

face sketch.

(2) After we estimate the P

linear combination

coefficients, we use these with face

eigenvectors in hybrid subspace to

synthesize reconstructed face image in

hybrid subspace.

(3) Reconstructed face image is obtained by

keeping the upper half of the reconstructed

image in hybrid subspace.

In recognition phase, we do the following steps:

(1) Build an OTSDF correlation filter for each

reconstructed face image from the probe

sketch image.

(2) Use the CMU PIE illumination variation

face images of each person as testing face

images template and matches this OTSDF

filter with each of them to get PCE score.

(3) Classify the reconstructed image as the

person with whom the resulting PCE score

is the highest.

(4) For recognition with

one-nearest-neighbour method (1NN), we

calculate the Euclidean distance between

the reconstructed face image and testing

template, classify the reconstructed face

image as the person with whose training

image it has the shortest distance.

3.2 Result

In order to see the performance of the proposed

method, we contrast it with 1NN classifier.

Moreover, we also use different number of

eigenfaces to see if the proposed method degraded

gracefully when the quality of reconstructed images

is getting worse. In addition, all the experiment

results are based on the first rank, i.e: we only take

the one with the highest score, both OTSDF and

1NN. Figure 9 shows the result.

FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID

EIGENANALYSIS FOR FACE SYNTHESIS

Figure 9: Classification rate with OTSDF and 1NN.

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

Percentage of eigenvectors in hybrid space used for reconstruction

OTSDF on Light

1NN on Light

OTSDF on NoLight

1NN on NoLight

3.3 Conclusion

The experimental results obtained are very

encouraging. When experimenting on PIE Light

database, which is a relatively easier task, we can get

100% recognition rate with either the OTSDF or

1NN method. However, OTSDF can achieve 100%

even when only 30% of eigenvectors are used, while

the 1NN can only achieve recognition rate of

87.69%.

When experimenting on the CMU PIE NoLight

dataset, which is a much more challenging task, the

OTSDF approach clearly outperformed 1NN in all

experiments clearly showing its capabilities to

perform illumination tolerant face recognition. From

these experimental results, we can conclude that our

proposed novel face synthesis from sketch approach

coupled with advanced correlation filters for face

recognition is a successful solution to this problem

and is more feasible to work in real world system

than the latest work proposed by (Tang, 2002, 2004).

4 FUTURE WORK

We are working to evaluate our algorithm on a

larger dataset such as the Notre Dame Face

Recognition Grand Challenge (Phillips, 2004) to see

how the proposed method performs in large scale

face database.

REFERENCES

W. Zhao, R. Chellappa, A. Rosenfeld and P. J. Phillips,

“Face Recognition: A Literature Survey”, CS-Tech

Report-4167, University of Maryland, 2000.

X. Tang and X. Wang, “Face Photo Recognition Using

Sketch”, Proc. of Int. Conf. Image Processing, 2002.

X. Tang and X. Wang, “Face Sketch Recognition”, IEEE

Trans. on Circuit System and Video Technology,

Vol.14, pp.50-57, 2004.

X. Tang and X. Wang, “Face Sketch Synthesis and

Recognition”, Proc. of Int. Conf. Computer Vision,

2003.

Q. Liu, X. Tang, H, Jin, H. Lu, and S. Ma, “A Nonlinear

Approach for Face Sketch Synthesis and Recognition”,

Proc. Of. IEEE Computer Society Conference on

Computer Vision and Pattern Recognition, 2005.

M.A. Turk and A. P. Pentland, “Face recognition using

eigenfaces”, presented at Computer Vision and Pattern

Recognition, 1991. Proceeding CVPR ’91., IEEE

Computer Society Conference on, 1991.

B.V.K. Vijaya Kumar, “Tutorial Survey of Composite

Filter designs for Optical Correlators,” Applied Optics,

vol. 31, pp. 4773-4801, 1992

A. Mahalanobis, B.V.K. Vijaya Kumar, and D. Casasent,

“Minimum average correlation energy filters,”

Applied Optics, vol. 26:3633-3640, 1987.

A. Mahalanobis, B.V.K. Vijaya Kumar, S. Song, S.R.F.

Sims, and J.F. Epperson, “Unconstrained correlation

filters,” Applied Optics, vol. 33:3751-3759, 1994.

B. V. K. V. Kumar, D. Carlson, and A. Mahalanobis,

“Optimal tradeoff synthetic discriminant function

(OTSDF) filters for arbitrary devices,” Opt. Lett., vol.

19, pp. 1556–1558, 1994.

P. J. Phillips, H. Moon, P. J. Rauss, and S. Rizvi, "The

FERET evaluation methodology for face recognition

algorithms", IEEE Transactions on Pattern Analysis

and Machine Intelligence, Vol. 22, No. 10, October

2000.

P. J. Phillips, P. J. Rauss, and S. Z. Der, " FERET (Face

Recognition Technology) Recognition Algorithm

Development and Test Results", October 1996. Army

Research Lab technical report 995.

P. J. Phillips, “Face Recognition Grand Challenge”,

presented at Biometric Consortium Conference, 2004

T. Sim, S. Baker, and M. Bsat “The CMU Pose,

Illumination, and Expression (PIE) Database of

Human faces,” Tech. Report CMU-RI-TR-01-02,

Robotics Institute, Carnegie Mellon University,

January (2001)

M. Savvides, B.V.K. Vijaya Kumar and P.K. Khosla,

"Robust, Shift-Invariant Biometric Identification from

Partial Face Images", Biometric Technologies for

Human Identification (OR51) 2004.

M. Savvides, B.V.K. Vijaya Kumar and P.K. Khosla,

“Face verification using correlation filters”, Proc. Of

the Third IEEE Automatic Identification Advanced

Technologies, 56-61, Tarrytown, NY, March 2002.

M. Savvides, C.Xie, N. Chu, B.V.K.Vijaya Kumar, C.

Podilchuk, A. Patel, A. Harthattu, R. Mammone,

“Robust Face Recognition using Advanced

Correlation Filters with Bijective-Mapping

Preprocessing”, Audio-Video Based Biometric Person

Authentication (AVBPA), July 2005.

ICEIS 2006 - HUMAN-COMPUTER INTERACTION