
MERGING, REPAIRING AND QUERYING INCONSISTENT
DATABASES WITH FUNCTIONAL AND INCLUSION
DEPENDENCIES
Luciano Caroprese, Sergio Greco and Ester Zumpano
DEIS, Universit
`
a della Calabria
87030 Rende, Italy
Keywords:
Data Integration, Inconsistent Databases, Consistent Query Answers.
Abstract:
In this paper a framework for merging, repairing and querying inconsistent databases is presented. The frame-
work, considers integrity constraints defining primary keys, foreign keys and general functional dependencies.
The approach consists of three steps: i) merge of the source databases by means of integration operators or
general SQL queries, to reduce the set of tuples coming from the source databases which are inconsistent with
respect to the constraints defined by the primary keys, ii) repair of the integrated database by completing and/or
cleaning the set of tuples which are inconsistent with respect to the inclusion dependencies (e.g. foreign keys),
and iii) compute consistent answers over repaired databases which could be still inconsistent with respect to
the functional dependencies. The complexity of merging, repairing and computing consistent answers will be
show to be polynomial and a prototype of a system integrating databases and computing queries over possible
inconsistent databases will be presented.
1 INTRODUCTION
The primary task of information integration consists
in providing a uniform integrated access to multi-
ple independent information sources, which are both
distributed and potentially heterogeneous and whose
contents are strictly related. However the integrated
view, constructed by integrating the information pro-
vided by the different data sources, could potentially
contain inconsistent data, i.e. it can violate some of
the constraints defined on the data.
Example 1 Consider the database consisting of the
relation Employee(Name, Age, Salary) where the at-
tribute Name is a key for the relation. Assume there
are two different instances for the relations Em-
ployee:
{Employee(Mary,28, 20),Employee(Peter,47, 50)}
{Employee(Mary,31, 30),Employee(Peter,47, 50)}
If the integration of the two relations
Employee
1
and Employee
2
is performed by
using the union operator (i.e. by considering
the union of the tuples in both the relations)
the following integrated relation is obtained:
{Employee(Mary,28, 20),Employee(Mary,31, 30),
Employee(Peter,47, 50)}
which does not anymore
satisfy the key constraint.
As showed in the previous example, in some case
the integrated database may be not consistent with re-
spect to the integrity constraints. In such a case there
are two possible solutions which have been investi-
gated in the literature (Agarwal et al., 1995; Arenas et
al., 1999; Bry, 1997; Dung, 1996; Greco et al., 2001;
Greco and Zumpano, 2000; Lin, 1996; Lin, 1996; Lin
and Mendelzon, 1999): repairing the database by in-
serting or deleting tuples, so that the resulting data-
base is consistent, or computing consistent answers
over the inconsistent database. Intuitively, a repair of
the database consists in deleting or inserting a min-
imal number of tuples so that the resulting relation
is consistent. The second approach, considering the
computation of consistent answer, is based on the fact
that, since the data are not consistent, answers may be
certain or uncertain.
Example 2 Consider again the integrated database
Employee reported in Example 1. In this case there
are two possible repaired databases each obtained by
deleting one of the two tuples whose value of the at-
tribute Name is Mary. As regards the answer to
the query asking for the age of Peter this is consti-
tuted by the certain set {47}, whereas the answer to
the query asking for the age of Mary produces the
following set of uncertain values {28, 31}. 2
Thus, in this paper we also consider, other than the
merging of databases, the repairing of databases and
the computation of consistent answers. In our frame-
work we consider integrity constraints defining pri-
38
Caroprese L., Greco S. and Zumpano E. (2006).
MERGING, REPAIRING AND QUERYING INCONSISTENT DATABASES WITH FUNCTIONAL AND INCLUSION DEPENDENCIES.
In Proceedings of the Eighth Inter national Conference on Enterprise Information Systems - DISI, pages 38-45
DOI: 10.5220/0002458900380045
Copyright
c
SciTePress

mary keys, functional dependencies and foreign keys.
As above explained, the motivation to consider gen-
eral functional dependencies, and special forms of
functional dependencies such as primary keys, is that
primary keys are used in the merging phase, whereas
functional dependencies are used to compute consis-
tent answers. Foreign keys are used to repair the data-
base so that the resulting database satisfy them. The
process can be performed by (i) completing the data-
base, i.e. by inserting tuples, and/or (ii) by cleaning
the database, i.e. by removing tuples.
The proposed framework for merging, repairing
and querying inconsistent databases with functional
and inclusion dependencies, has been implemented
in a system prototype, developed at the University of
Calabria.
2 DATABASE INTEGRATION
AND QUERYING
Integrating and querying data from different sources
consists of three main steps: the first in which the var-
ious relations are merged together to reduce the set
of inconsistent tuples; the second in which some tu-
ples are removed or inserted into the database in or-
der to satisfy some of the integrity constraints; the
third in which the query answer, consisting of the
set of certain and uncertain tuples, is computed. Be-
fore formally introducing the problems related to the
merging, repairing and querying of inconsistent data-
bases let us introduce some basic definitions and no-
tations. Generally, a database D has associated a
schema DS = Rs, IC which defines the intentional
properties of D: Rs denotes the structure of the rela-
tions and IC contains the set of integrity constraints.
In this paper we concentrate on integrity constraints
consisting of functional dependencies, including con-
straints defining primary keys, and inclusion depen-
dencies expressing foreign keys. Thus, our set of in-
tegrity constraints IC can be partitioned into two sets:
FD, consisting of functional dependencies, and FK,
consisting of foreign keys, i.e. IC = FD ∪ FK.
Moreover, we denote with PK the subset of the func-
tional dependencies defining primary keys.
Given a relation R,afunctional dependency X →
Y over R can be expressed by a formula of the form
∀(X, Y, Z, U, V )[ R(X, Y, U) ∧ R(X, Z, V ) ⊃
Y = Z ]
where X, Y, Z, U, V are lists of variables and Y,Z
may be empty lists.
Let D be a database, R a relation of D and t a tuple
in R, then we denote by: i) attr(R) the set of attributes
of R
, ii) pkey(R) the set of attributes in the primary
key of R, iii) fd(R) the set of functional dependen-
cies of R,iv)pkey(t) the values of the key attributes
of t.
Databases Merging. The database merging prob-
lem consists in the merging of k databases D
1
=
{R
1,1
, ...R
1,n
1
}, ..., D
k
= {R
k,1
, ...R
k,n
k
}. For the
sake of simplicity we assume that all databases con-
tain the same number of relations (i.e. n
1
= ··· =
n
k
= n) and that for every 1 ≤ j ≤ k, R
1,j
, ..., R
k,j
refer to the same concept. The integrated database D
consists of n relations T
1
, ..., T
n
where every T
j
is ob-
tained by merging the relations R
1,j
, ..., R
k,j
. Thus,
the database integration problem consists in the inte-
gration of a set of relations R
1,j
, ..., R
k,j
into a rela-
tion T
j
by means of a (binary) integration operator ,
i.e. computes T
j
=(...(R
1,j
R
2,j
) ···) R
k,j
.We
assume that relations associated with the same class
of objects have been homogenized with respect to a
common ontology, i.e. attributes denoting the same
concepts have the same name (Yan and Ozsu, 1999).
We say that two homogenized relations R and S, as-
sociated with the same concept, are overlapping if
pkey(R)=pkey(S). In the following we assume
that relations associated with the same class of objects
are overlapping.
Several merge operators have been proposed in the
literature. We recall here the Match Join operator
(Yan and Ozsu, 1999), the Merging by Majority oper-
ator (Lin and Mendelzon, 1999), the Merge operator
(Greco et al., 2001), the Prioritized Merge operator
(Greco et al., 2001). Before presenting, in an informal
way, these operators we introduce some preliminary
definition and formally define desirable properties of
integration operators.
Definition 1 Given two relations R and S such that
attr(R) ⊆ attr(S) and two tuples t
1
∈ R and t
2
∈
S, we say that t
1
is less informative than t
2
(t
1
t
2
)
if for each attribute A in attr(R), t
1
[A]=t
2
[A] or
t
1
[A]=⊥, where ⊥ denotes the null value. Moreover,
given two relations R and S, we say that R S if
∀t
1
∈ R, ∃t
2
∈ S s.t. t
1
t
2
. 2
Definition 2 Let R and S be two relations, a binary
operator such that: (i) attr(R S)=attr(R) ∪
attr(S), (ii) RS R S, (iii) (R R)=
R (idempotency). is called integration or merge op-
erator. Moreover, an integration operator is said to
be (i) commutative,ifR S = S R. (ii) associa-
tive,if(R S) T = R (S T ). (iii) complete
(or lossless), if for all R and S, R (R S) and
S (R S)
;(iv)dependency preserving, if for all R
and S,is(R S) |=(fd(R) ∩ fd(S)); (v) correct if
∀t ∈ R S ∃t
s.t. (t
∈ R or t
∈ S) and t
t 2
Informally, if an integration operator is both correct
and complete it preserves the information provided by
MERGING, REPAIRING AND QUERYING INCONSISTENT DATABASES WITH FUNCTIONAL AND INCLUSION
DEPENDENCIES
39

the sources. In fact, it could modify some input tuples
by replacing null values with not null ones, but all the
associations of not null values which were contained
in the source relations will be inserted into the result
(completeness) and no association of not null values
which was not contained in the source relations will
be inserted into the result (correctness). Moreover,
note that integrating more than two relations by means
of a not associative integration operator, may give dif-
ferent results, if the integration operator is applied in
different orders. Thus, even if the associative property
is desirable, it is not satisfied by several operators de-
fined in the literature.
Repairing inconsistent databases. Let us first in-
troduce the formal definition of consistent database
and repairs.
Definition 3 Given a database schema DS =
Rs, IC and a database instance D over Rs, we say
that D is consistent if D |= IC, i.e. if all integrity
constraints in IC are satisfied by D, otherwise it is
inconsistent. 2
Example 3 The database of Example 1, derived from
the union of the two source databases, is inconsistent
as the functional dependency
∀(K, A
1
,S
1
,A
2
,S
2
)[ Employee(K, A
1
,S
1
) ,
Employee(K, A
2
,S
2
) ⊃ A
1
= A
2
,S
1
= S
2
]
stating that K is a key for the relation Employee is
not satisfied. 2
Informally, a repair R for a (possibly inconsistent)
database D is a minimal, consistent set of insert and
delete operations (denoted, respectively, by R
+
and
R
−
) which makes D consistent. Given a repair R,
R
+
denotes the set of tuples which will be added to
the database whereas R
−
denotes the set of tuples of
D which will be deleted.
Given two pairs of sets of atoms S =(S
+
,S
−
) and
R =(R
+
,R
−
), we say that S ⊆ R if both S
+
⊆ R
+
and S
−
⊆ R
−
. We also say that S ⊂ R if S = R and
S ⊆ R.
Definition 4 (Arenas et al., 1999) Let DS =
Rs, IC be a database schema and D be a (possi-
bly inconsistent) database over Rs, then a repair for
D is a pair of sets of atoms (R
+
,R
−
) such that: (i)
R
+
∩R
−
= ∅; (ii) D ∪R
+
−R
−
|= IC and (iii) there
is no repair (S
+
,S
−
) ⊂ (R
+
,R
−
) .
The database R(D)=D∪R
+
−R
−
, obtained from
the application of R to D, will be called the repaired
database. 2
Thus, repaired databases are consistent databases
which are derived from the source database by means
of a minimal set of insertion and deletion of tuples.
Example 4 Assume we are given the database D =
{p(a),p(b),q(a),q(c)}, with the inclusion depen-
dency: (∀ X)[p(X) ⊃ q(X)]. D is incon-
sistent since p(b) ⊃ q(b) is not satisfied. The
repairs for D are R
1
=({q(b)}, ∅) and R
2
=
(∅, {p(b)}) producing, respectively, the repaired data-
bases R
1
(D)={p(a),p(b),q(a),q(c),q(b)} and
R
2
(D)={p(a),q(a),q(c)}. 2
Queries over inconsistent databases. A (rela-
tional) query over a database defines a function from
the database to a relation. It can be expressed by
means of alternative equivalent languages such as re-
lational algebra, ‘safe’ relational calculus or ‘safe’
non-recursive Datalog (Abiteboul and al., 1994; Ull-
man, 1998) (i.e., safe Datalog without disjunction,
classical negation and recursion). Thus, a query is
a pair (g, P), where P is an expression of the query
language and g is a predicate symbol specifying the
output (derived) relation.
Definition 5 Given a database schema DS =
Rs, IC and a database D over Rs, an atom A is
true (resp. false) with respect to (D, IC) if A belongs
to all repaired databases (resp. there is no repaired
database containing A). The set of atoms which are
neither true nor false are undefined. 2
Thus, true atoms appear in all repaired databases
(Arenas et al., 1999), whereas undefined atoms ap-
pear in a proper subset of repaired databases.
Definition 6 Given a database schema DS =
Rs, IC and a database D over Rs, the application
of IC to D, denoted by IC(D), defines three distinct
sets of atoms: the set of true atoms IC(D
)
+
, the set
of undefined atoms IC(D)
u
and the set of false atoms
IC(D)
−
. 2
Definition 7 Given a database schema DS =
Rs, IC, a database D over Rs and a query Q =
(g, P), the consistent answer of the query Q on the
database D, denoted as Q(D, IC), gives three sets,
denoted Q(D, IC)
+
, Q(D, IC)
−
and Q(D, IC)
u
,
containing, respectively, the sets of g-tuples which are
true (i.e. belonging to Q(D
) for all repaired data-
bases D
), false (i.e. not belonging to Q(D
) for all
repaired databases D
) and undefined (i.e. set of tu-
ples which are neither true nor false). 2
3 DATABASE INTEGRATION
The Match Join Operator. The Match Join opera-
tor,
, proposed in (Yan and Ozsu, 1999), manufac-
tures tuples in the integrated relation by performing
the outer-join of the ValSetof each attribute, where
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
40

the ValSetof an attribute A is the union of the pro-
jections of each overlapping relations on {K, A}.
Example 5 Consider the following two overlapping
relations S
1
and S
2
:
K Title Author
1 Moon Greg
2 Money Jones
3 Sky Jones
S
1
K Title Author Year
3 F lowers Smith 1965
4 Sea Taylor 1971
7 Sun Steven 1980
S
2
and suppose the attribute Author is functionally de-
pendent on the attribute Title, i.e. Title → Author.
The relation obtained T by applying the Match Join
operator to the relations S
1
and S
2
, i.e. T = S
1
S
2
,
is the following:
K Title Author Year
1 Moon Greg ⊥
2 Money Jones ⊥
3 Sky Jones 1965
3 Sky Smith 1965
3 F lowers Smith 1965
3 F lowers Jones 1965
4 Sea Taylor 1971
7 Sun Steven 1980
T
where ⊥ denotes the null value.
The Match Join operator is complete, but it is not
correct, since it mixes values coming from different
tuples with the same key in all possible ways. As a
consequence, when applying the Match Join operator
to S
1
and S
2
we obtain an integrated view T violating
the functional dependency Title → Author. Thus
the Match Join operator produces tuples containing
associations of values that may be not present in any
original relation and the integration process may gen-
erate a relation which is not anymore consistent w.r.t.
the functional dependency.
The Merging by Majority Operator. The Merging
by Majority operator, proposed in (Lin and Mendel-
zon, 1999) tries to remove conflicts taking into ac-
count the majority view of the knowledge bases, i.e. it
maintains the (not null) value which is present in the
majority of the knowledge bases. Thus the operator
constructs an integrated relation containing general-
ized tuples, i.e. tuples where each attribute value is a
simple value, if the information respects the majority
criteria, or a set, if the technique doesn’t resolve the
conflict.
Example 6 Consider the database consisting of the
relation Bib(Author, T itle, Y ear) which collect in-
formation regarding author, title and year of publica-
tion of papers. Assume to have the following three
database instances:
{Bib(John, T
1
, 1980),Bib(Mary, T
2
, 1990)},
{Bib(John, T
1
, 1981),Bib(Mary, T
2
, 1990)},
{Bib(John, T
1
, 1980),Bib(F rank, T
3
, 1990)}.
From the integration of the above three
databases we obtain the database Bib.
{Bib(John, T
1
, 1980),Bib(Mary, T
2
, 1990),Bib(
Frank,T
3
, 1990)}.
Note that, the Merging by Majority operator re-
moves the conflict about the year of publication of the
paper T
1
written by the author John observing that
two of the three source relations, that have to be in-
tegrated, store the value 1980; thus the information
that is maintained is the one which is present in the
majority of the knowledge bases.
However, the Merging by Majority technique does
not resolve conflicts in all cases since information is
not always present in the majority of the databases
and, therefore, it is not always possible to choose
among alternative values. In this case the integrated
database contains generalized tuples.
For instance, the merging of the two relation S
1
and S
2
of Example 6 gives the “nested” relation
{Bib(John,T
1
, {1980, 1981}),Bib(Mary, T
2
, 1990),
Bib(Frank,T
3
, 1990)}.
Here the first tuple states that the year of publica-
tion of the book written by John with title T
1
can be
one of the values belonging to the set {1980, 1981}.
Thus the Merging by Majority approach could fail
when, for a field, the database majority does not agree
on a value. In this case, for each of this field, a set of
possible values is associated in the integrated data-
bases. The Merging by Majority operator is correct,
but it is not complete.
The Merge Operator. Given two overlapping rela-
tions S
1
and S
2
, the Merge operator, introduced in
(Greco et al., 2001), applied to S
1
and S
2
, S
1
S
2
,
produces a relation S obtained by completing the in-
formation coming from each input relation with that
coming from the other one. More specifically, it com-
putes the full outer join and extends tuples coming
from S
1
(resp. S
2
) with the values of tuples of S
2
(resp. S
1
) having the same key.
Example 7 Consider the relations S1 and S2 re-
ported in the Example 5. The relation T , obtained
by merging S
1
and S
2
through the merge operator,
i.e. T = S
1
S
2
, is the following:
K Title Author Year
1 Moon Greg ⊥
2 Money Jones ⊥
3 Sky Jones 1965
3 F lowers Smith 1965
4 Sea Taylor 1971
7 Sun Steven 1980
T
MERGING, REPAIRING AND QUERYING INCONSISTENT DATABASES WITH FUNCTIONAL AND INCLUSION
DEPENDENCIES
41
Note that the integrated relation does not violate the
functional dependency Title → Author. 2
The Merge operator is correct and complete. More-
over, on the contrary of the Match Join operator ,
which mixes values coming from different tuples with
the same key in all possible ways, it only tries to de-
rive unknown values so that number of integrated tu-
ples violating the key constraint is reduced.
The Prioritized Merge Operator. The Prioritized
Merge operator, , introduced in (Greco et al., 2001),
is an asymmetric operator which, if conflicting tuples
are detected, gives preference to data coming from the
source on which the user expressed preference. More
specifically, given two source relations, S
1
and S
2
,
the prioritized merge operator applied to S
1
and S
2
,
S = S
1
S
2
, produces a relation S which includes
all tuples of the left relation and only the tuples of the
right relation whose key does not identify any tuple in
the left relation. Moreover, only tuples ‘coming’ from
the left relation are extended since tuples coming from
the right relation, joining some tuples coming from
the left relation, are not included. Thus, when inte-
grating relations conflicting on the key attributes, the
prioritized merge operator gives preference to the tu-
ples of the left side relation and completes them with
values taken from the right side relation.
Example 8 Consider the source relations S
1
and S
2
of Example 5. The relation T = S
1
S
2
is:
K Title Author Year
1 Moon Gr eg ⊥
2 Money Jones ⊥
3 Sky J ones 1965
4 Sea Taylor 1971
7 Sun Steven 1980
T
The merged relation obtained in this case differs
from the one of Example 7 because it does not contain
the tuple (3,Flowers,Smith,1965) coming from
the right relation S
2
. 2
Obviously, the prioritized merge operator is correct,
but it is not complete as in the presence of conflicting
tuples it holds the values coming from the left rela-
tion. Moreover, given two overlapping relations S
1
and S
2
, then (i) S
1
S
2
⊆ S
1
S
2
, (ii) S
1
S
2
=
(S
1
S
2
) ∪ (S
2
S
1
) and (iii) S
1
S
1
= S
1
.
More General Techniques. In some cases the use
of predefined operators does not satisfy the intended
integration strategy. Thus, we present a more general
merging strategy allowing to specify for each attribute
A the integration task to be performed. Given a set of
homogenized relations S
1
, ..., S
n
,areconciled rela-
tion S is s.t.: i) attr(S)=
n
i=1
attr(S
i
), ii) it con-
tains all tuples t ∈ S
i
, 1 ≤ i ≤ n, completed with
⊥ for all attributes belonging to attr(S) − attr(S
i
).
Thus, starting from the reconciled relation S, we con-
sider a more general strategy based on i) the collection
of tuples with the same value for the key attributes
into a ‘nested’ tuple where each non key attribute, say
A, contains the list [a
1
, ..., a
n
] of the values of the at-
tribute A present in the tuples of S which have to be
merged and ii) the application of a polynomial func-
tion f
i
to [a
1
, ..., a
n
]. The specialization of the func-
tions f
i
permits us to express most of the integration
operators defined in literature. For instance, the merg-
ing by majority technique is obtained by specializing
all f
i
to select the element which occurs a maximum
number of times in the list. In other cases the function
f
i
computes a value such as the maximum, minimum,
average, etc.
Fact 1 The complexity of constructing the merged
database by means of an integration operators is
polynomial time. 2
4 COMPUTING DATABASE
REPAIRS
In this section we consider the computation of repairs
with respect to a set of inclusion dependencies.
An inclusion dependency is an integrity constraint
of the form ∀(X, Y )[p(X, Y ) ⊃∃Zq(X, Z)] whose
meaning in that if there exists a tuple (x, y) in p, then
there must exist a tuple (x, z) in q for some value z.
In order to repair a database not satisfying an inclu-
sion dependency of the above form, two solutions can
be performed. In more details, for every tuple (x, y)
of p such that there is no tuple (x, z) (for all possi-
ble values z)inq i) delete the tuple (x, y) from p or
insert a tuple (x, ⊥
1
) into q where ⊥
1
is a null value
if the corresponding attribute is not a foreign key or
a new value different from all values present in the
database. In the first case we say that the database is
cleaned, as we consider the inconsistent data as not
correct, whereas, in the second case we say that the
database is completed, as we consider the data which
are inconsistent (with respect to inclusion dependen-
cies) as correct.
Proposition 1 Let D be a database, Q =(g, P) a
query and IC a set of inclusion dependencies. Then,
(i) a repair for D always exists, (ii) the computation
of a repair, selected nondeterministically, can be done
in polynomial time. 2
The above proposition can be easily proved as a
cleaning repair always exists and it can be computed
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
42
by deleting tuples, one-at-time, non satisfying inclu-
sion dependencies.
Theorem 2 Let D be a database and IC a set of in-
clusion dependencies defining foreign keys. Then, (i)
a completing repair for D always exists, (ii) the com-
putation of a completing repair, can be done in poly-
nomial time. 2
5 QUERYING INCONSISTENT
DATABASES
Given a query Q = g,P and a consistent data-
base D, the answer to the query Q applied to D is
Q(D)={t|g(t) ∈P(D)}, returns the set of g-tuples
belonging to the result obtained from the evaluation
of P over D. Clearly, in this case the query Q(D)
defines a function from the database to a relation.
The answer to a query Q over a database D
which may be inconsistent with respect to a set of
integrity constraints is Q(D, IC)={{t|g(t) ∈
P(R(D))}|∃R ∈R(D)}, where R(D) is the set
of repairs of D and R(D) is the repaired database
w.r.t R. Thus, in this case we may have more than
one outcome, as we evaluate the query over all pos-
sible repaired databases. Therefore, in this case the
Q(D, IC) defines a multi-valued function from the
database to a set of relations.
A deterministic answers can be obtained by con-
sidering either the union or the intersection of the
sets in Q(D, IC). More specifically, the certain
answer consists of the tuples belonging to all sets
in Q(D, IC), whereas the possible answer consists
of the tuples belonging to some set in Q(D, IC).
Therefore, the certain answer is Q(D, IC)
c
=
M∈Q(D,IC)
M, whereas the possible answer is
Q(D, IC)
p
=
M∈Q(D,IC)
M. As a consequence,
the uncertain answer is Q(D, IC)
u
= Q(D, IC)
p
−
Q(D, IC)
c
.
For instance, in Example 4, the set of true tuples are
those belonging to the intersection of the two models,
that is p(a), q(a) and q(c), whereas the set of unde-
fined tuples are those belonging to the union of the
two models and not belonging to their intersection.
Example 9 Consider the integrated rela-
tion Employee of Example 1. There
are two alternative repairs which make
the database consistent: R
1
= {},
{Employee(Mary,28, 20)} which deletes from
the database the tuple Employee(Mary,28, 20)
and R
1
= {}, {Employee(Mary,31, 30)}
which deletes from the database the tuple
Employee(Mary,31, 30). The query ask-
ing for name and age of every employee re-
turns {(Peter,47)} as certain answer and
{(Mary,28), (Mary,31)} as uncertain answer. 2
Although the computation of certain (and possible
or uncertain) answers may be computationally expen-
sive for general constraints, for simple classes of in-
tegrity constraints the computation can be very effi-
cient.
Theorem 3 Let D be a database, FD a set of func-
tional dependencies over D, and Q a query. Then,
Q(D, FD) can be computed in polynomial time. 2
6 A SYSTEM PROTOTYPE
The framework for merging, repairing and querying
inconsistent databases with functional and inclusion
dependencies, presented in the previous sections has
been implemented in a system prototype, developed
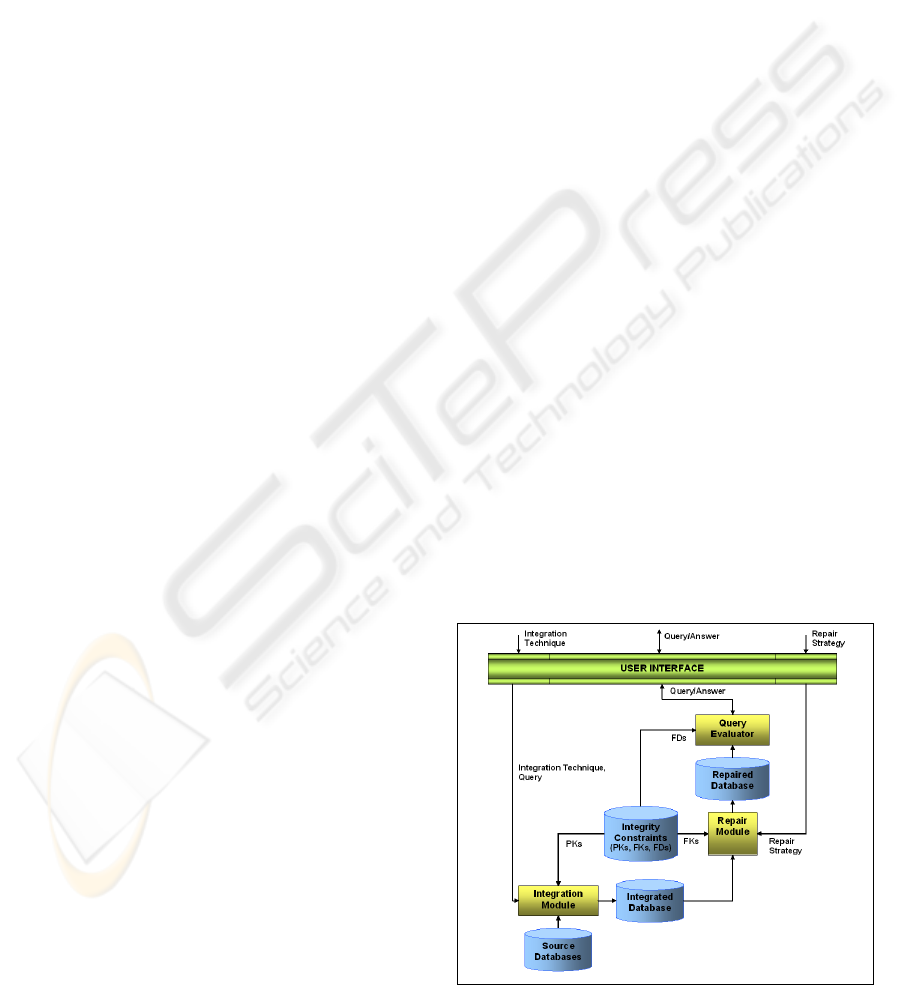
at the University of Calabria. The overall architecture
is reported in Figure 1. This system receives in input
an Integration Technique IT , consisting of a prede-
fined operator or a set of SQL queries, a query Q and
a repairing strategy RS (completing or cleaning) and
outputs the answer Ans. The answers is partitioned
into two parts: certain answers (set of tuples which
are always true) and uncertain answers. The system
is currently able to implement many of the integration
operators, proposed in literature, such as the match
join, the merging by majority, the merge and the pri-
oritized merge operator. In more details, the integra-
tion methodology can be selected among the merging
operators, defined in the literature, or most flexibly,
the user can specify SQL queries, reflecting real user
needs.
Figure 1: System architecture.
MERGING, REPAIRING AND QUERYING INCONSISTENT DATABASES WITH FUNCTIONAL AND INCLUSION
DEPENDENCIES
43

In the following we describe the main modules
composing the system.
User Interface (UI). This module receives an Inte-
gration technique IT , (i.e. a predefined operator
or a set of SQL queries), a query Q and a repair
strategy RS (completing or cleaning) and outputs
the answer Ans.
Integration Module (IM). This module receives
in input the Integration Technique or a set of
SQL queries, and a (possible empty) query Q and
constructs the corresponding integrated database
(IDB). In particular if both the query Q and the
integration technique IT is provided the Integrated
Database is constructed w.r.t. the set of relations
directly or even indirectly involved in Q. If just an
integration technique IT is provided in input the
Integrated Database is constructed w.r.t. the Source
Databases.
Repairing Module (RM). This module is respon-
sible of solving foreign key inconsistencies using
the strategy specified by the input parameter RS
(cleaning or completing). In more details, it imple-
ments the repair strategy depicted in Section 4, by
completing or cleaning the inconsistent database so
that obtain a database consistent w.r.t the set of for-
eign keys.
The database obtained by cleaning or completing
the IDB is called CDB.
Query Evaluator Module (QEM). This module
receives the query Q and the set of functional de-
pendencies and returns the answer, Ans, to the user
interface. In particular, this module, implements
the technique for managing inconsistent database,
presented in Section 5, so that providing an answer
evidencing the set of certain and uncertain tuples.
6.1 Implementing Merge Operators
In this section we show how to express integration
operators. We consider two relations S
1
(K, A, B)
and S
2
(K, A, C) where K, A, B and C denotes sets
of attributes. In particular, K = {K
1
, ..., K
m
} =
pkey(S
1
)=pkey(S
2
) denotes the key of the two re-
lations, A = {A
1
, ..., A
n
} = attr(S
1
)∩attr(S
2
)−K
is the set of shared attributes not belonging to the key,
B = {B
1
, ..., B
p
} = attr(S
1
) − attr(S
2
) and C =
{C
1
, ..., C
q
} = attr(S
2
) − attr(S
1
) denote the set of
attributes appearing in only one of the two relations.
For the sake of brevity, we often use the set attributes
K, A, B and C instead of the single attributes; for in-
stance, we use S
1
.K = S
2
.K to denote the equality
condition S
1
.K
1
= S
2
.K
1
∧···∧S
1
.K
m
= S
2
.K
m
.
Moreover, in the following we will use use NULL(B)
to assign null values to the attributes in B and the
standard operator COALESCE(A
1
, ..., A
n
) to select the
first not null value in the sequence.
The Match Join operator. The Match Join opera-
tor can be easily expressed by means of the following
SQL statement:
CREATE VIEW S(K, A, B, C) AS
SELECT K, A, B, NULL(C) FROM S
1
UNION
SELECT K, A, NULL(B),C FROM S
2
;
for each X
i
∈ A ∪ B ∪ C
CREATE VIEW T
i
(K, A
i
) AS
SELECT K, X
i
FROM S
WHERE X
i
IS NOT NULL
SELECT T
1
.K, T
1
.X
1
, ..., T
m
.X
n+m+q
FROM T
1
OUTER JOIN T
2
ON T
1
.K = T
2
.K...
OUTER JOIN T
n
ON T
n−1
.K = T
n
.K;
The Merging by Majority Operator. The SQL
statement expressing the Merging by Majority oper-
ator is the following:
CREATE VIEW S(K, A, B, C) AS
SELECT K, A, B, NULL(C) FROM S
1
UNION
SELECT K, A, NULL(B),C FROM S
2
;
for each X
i
∈ A ∪ B ∪ C {
CREATE VIEW W
i
(K, X
i
, Counter) AS
SELECT K, X
i
, COUNT(∗) FROM S
GROUP BY (K, X
i
);
CREATE VIEW T
i
(K, X
i
) AS
SELECT K, X
i
FROM W
i
WHERE NOT EXISTS(
SELECT
*
FROM W
i
AS W
i
WHERE W
i
.K = W
i
.K AND
W
i
.Counter < W
i
.Counter); }
SELECT T
1
.K, T
1
.X
1
, ..., T
n+p+q
.X
n+p+q
FROM T
1
, ..., T
n+p+q
WHERE T
1
.K = T
2
.K AND ...
AND T
n+p+q−1
.K = T
n+p+q
.K;
The Merge operator. The Merge operator can be
easily expressed by means of the following SQL state-
ment:
SELECT S
1
.K, S
1
.B, COALESCE(S
1
.A
1
,S
2
.A
1
), ...,
COALESCE(S
1
.A
n
,S
2
.A
n
),S
2
.C
FROM S
1
LEFT OUTER JOIN S
2
ON S
1
.K = S
2
.K
UNION
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
44

SELECT S
2
.K, S
1
.B, COALESCE(S
2
.A
1
,S
1
.A
1
), ..,
COALESCE(S
2
.A
n
,S
1
.A
n
),S
2
.C
FROM S
1
LEFT OUTER JOIN S
2
ON S
1
.K = S
2
.K
The Prioritized Merge operator. The Prioritized
Merge operation S
1
S
2
, can be easily expressed by
means of an SQL statement, as follows:
SELECT S
1
.K, S
1
.B, COALESCE(S
1
.A
1
,S
2
.A
1
), ..,
COALESCE(S
1
.A
n
,S
2
.A
n
),S
2
.C
FROM S
1
LEFT OUTER JOIN S
2
ON S
1
.K = S
2
.K
UNION
SELECT S
2
.K, NULL(B),S
2
.A, S
2
.C
FROM S
2
,S
1
WHERE S
2
.K NOT IN (SELECT S
1
.K FROM S
1
)
6.2 Computing Consistent Answer
Given a query Q the computation of the consistent
answer, Consistent
Ans, is performed as follows:
i) firstly, the relation Ans, obtained by evaluating the
query Q over the (partial) repaired database and con-
taining both “certain” and “undefined” tuples is con-
structed; ii) secondly, the relation Inconsistent
Ans
containing the tuples of Ans which do not sat-
isfy some of the functional dependency involv-
ing attributes in Q, is constructed; iii) finally, the
Consistent
Ans, is carried out by selecting tuples
of Ans which are not in Inconsistent
Ans. Con-
sider, for instance, the Example 1 with the functional
dependency Name → Age, Salary and suppose to
perform a query asking for the name and the age of
Employees. The relation Ans is obtained by trivially
selecting Name and Age from Employee, whereas
the relation Inconsistent
Ans can be obtained by
means of the following SQL view:
CREATE VIEW Inconsistent Ans AS
SELECT Ans.∗ FROM Ans, Employee E
WHERE Ans.Name = E.Name
AND Ans.Age <>E.Age
The consistent answer, Consistent R, can be ob-
tained by means of the following SQL view:
CREATE VIEW Consistent Ans AS
SELECT ∗ FROM Ans
EXCEPT
SELECT ∗ FROM Inconsistent
Ans
REFERENCES
Abiteboul, S., Hull, R., Vianu, V. Foundations of Data-
bases. Addison-Wesley, 1994.
Agarwal, S., Keller, A. M., Wiederhold, G., Saraswat,
K., Flexible Relation: an Approach for Integrating
Data from Multiple, Possibly Inconsistent Databases.
ICDE, 1995.
Arenas, M., Bertossi, L., Chomicki, J., Consistent Query
Answers in Inconsistent Databases. Proc. PODS
1999, pp. 68–79, 1999.
Baral, C., Kraus, S., Minker, J., Combining Multiple
Knowledge Bases. IEEE-TKDE, 3(2): 208-220 (1991)
Breitbart, Y., Multidatabase interoperability. Sigmod
Record 19(3) (1990), 53–60.
Bry, F., Query Answering in Information System with In-
tegrity Constraints,IICIS, pp. 113-130, 1997.
Cali, A., Calvanese, D., De Giacomo, G., Lenzerini, M.,
Data Integration under Integrity Constraints. CAiSE,
pp. 262-279, 2002.
Dung, P. M. ,Integrating Data from Possibly Inconsistent
Databases. COOPIS, pp. 58-65, 1996.
Grant, J., Subrahmanian, V. S., Reasoning in Inconsistent
Knowledge Bases. IEEE-TKDE, 7(1): 177-189, 1995.
Greco, S., Zumpano, E., Querying Inconsistent Database
LPAR, pp. 308-325, 2000.
Greco, G., Greco, S., Zumpano, E., A Logic Programming
Approach to the Integration, Repairing and Querying
of Inconsistent Databases. ICLP pp. 348-364, 2001.
Greco, S., Pontieri, L., Zumpano, E., Integrating and Man-
aging Conflicting Data. Ershov Memorial Conference
pp. 349-362, 2001.
Levy, A., Rajaraman, A., Ordille, J., Querying heteroge-
neous nformation sources using source descriptions.
VLDB, pp. 251–262, 1996.
Lin, J., Mendelzon, A. O., Knowledge Base Merging by
Majority, in R. Pareschi and B. Fronhoefer (eds.), Dy-
namic Worlds, Kluwer, 1999. Kluwer, 1999.
Lin, J., A Semantics for Reasoning Consistently in the Pres-
ence of Inconsistency. AI, 86(1), pp. 75-95, 1996.
Lin, J., Integration of Weighted Knowledge Bases. Artificial
Intelligence, Vol. 83, No. 2, pages 363-378, 1996.
Pradhan, S., J. Minker, J., Subrahmanian, V.S., Combining
Databases with Prioritized Information JIIS, 4(3), pp.
231-260, 1995.
Subrahmanian, V. S., Amalgamating Knowledge Bases.
ACM-TODS, Vol. 19, No. 2, pp. 291-331, 1994.
Yan, L.L., Ozsu, M. T., Conflict Tolerant Queries in Aurora
Coopis, pp. 279-290, 1999.
Ullman, J. D., Principles of Database and Knowledge-
Base Systems, Vol. 1, Computer Science Pressingness,
1998.
Wiederhold, G., Mediators in the architecture of future
information systems. IEEE Computer 25(3): 38–49,
1992.
MERGING, REPAIRING AND QUERYING INCONSISTENT DATABASES WITH FUNCTIONAL AND INCLUSION
DEPENDENCIES
45
