A FORMAL APPROACH TO DETECTING SHILLING

BEHAVIORS IN CONCURRENT ONLINE AUCTIONS

Yi-Tsung Cheng and Haiping Xu

Computer and Information Science Department

University of Massachusetts Dartmouth

North Dartmouth, MA 02747

Keywords: Concurrent online auctions, Shilling behaviors, Model checking, Linear temporal logic (LTL).

Abstract: Shilling behaviors are one of the most serious fraud problems in online auctions, which make winning

bidders have to pay more than what they should pay for auctioned items. In concurrent online auctions,

where multiple auctions for the same type of items are running simultaneously, shilling behaviors can be

even more severe because detecting, predicting and preventing such fraudulent behaviors become very

difficult. In this paper, we propose a formal approach to detecting shilling behaviors in concurrent online

auctions using model checking techniques. We first develop a model template that represents two concurrent

online auctions in Promela. Based on the model template, we derive an auction model that simulates the

bidding processes of two concurrent auctions. Then we use the SPIN model checker to formally verify if the

auction model satisfies any questionable behavioral properties that are written in LTL (Linear Temporal

Logic) formulas. Thus, our approach simplifies the problem of searching for shilling behaviors in concurrent

online auctions into a model checking problem. Finally, we provide a case study to illustrate how our

approach can effectively detect possible shill bidders.

1 INTRODUCTION

In traditional economic theory, auction can be used

to determine the value of a commodity that is

difficult to tag a price. The commodity can be a

physical product, such as artwork and antiques; or it

can be a virtual product, for example, spectrum

licenses and procurement contracts. The most

commonly used types of auctions include English

auction, Dutch auction, sealed first-price auction,

and sealed second-price auction. Among them, only

English auction is adopted in online auction houses.

In an English auction, participants can openly

observe other people’s bids and then bid against

each other. The following bidding price must be

higher than the previous one. The auction ends

when the bidding reaches a point where no one

wants to beat the current highest price. So, in an

English auction, a bidder can bid multiple times

while the bidding price ascends. The seller of the

auctioned item can set a pre-determined reserve

price. If the final bidding price is lower than the

reserve price, the seller can reserve the right of not

selling the auctioned item.

The characteristic of multiple bids and ascending

bidding price in English auctions has made this

auction type very popular, but it also makes shilling

behaviors very common in online auctions.

There are two main kinds of shilling behaviors:

reserve price shilling and competitive shilling

(Kauffman and Wood, 2000). In reserve price

shilling, a seller sets a low reserve price and pretends

to be normal bidders to put in bids, in order to drive

up the bidding price to his own evaluation of the

item. Usually the lower reserve price the seller sets

the cheaper fee he has to pay to the auction house. In

this case, the seller can avoid paying higher reserve

price fee. In competitive shilling, a seller also

pretends to be normal bidders, and constantly

monitors the bidding process and puts in fake bids to

drive up the bidding price; however, the objective of

doing this is to make potential buyers pay extra

money to win their bids instead of paying less

reserve price fee. Although the objectives of these

two behaviors are different, their distinction is not

always very clear. For example, a reserve-price-

shilling seller might still want to drive up the

bidding price, even after it has already reached the

375

Cheng Y. and Xu Computer H. (2006).

A FORMAL APPROACH TO DETECTING SHILLING BEHAVIORS IN CONCURRENT ONLINE AUCTIONS.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - ISAS, pages 375-381

DOI: 10.5220/0002460803750381

 SciTePress

seller’s own evaluation of the item. Notice that

normally the reserve price shilling only affects the

auction houses; while the competitive shilling affects

all bidders in the market. It is obvious that the

competitive shilling causes a greater harm to the

auction market than the reserve price shilling. In

addition, shilling behaviors involved in concurrent

online auctions, where multiple auctions for the

same type of items are running simultaneously, are

much more difficult to detect than shilling behaviors

occur in a standalone auction. Thus, in this paper, we

focus on studying competitive shilling behaviors in

concurrent online auctions.

There is very little previous work on shill

detection for online auctions. Wang and his

colleagues showed that private value English

auctions with shill bidding can result in a higher

expected seller profit than other auction formats

(Wang et al., 2002). This explains why in online

auction houses like eBay, shilling behaviors have

become a very serious problem that cannot be

ignored. The authors proposed a commission fee

mechanism in which the auctioneer charges the

seller a commission fee based on the difference

between the winning bid and the seller’s reserve

price. This approach can make shill bidding un-

profitable, but it could be unfair to sellers’ interests,

especially when the sellers are not shilling at all.

Kauffman and Wood used a statistical approach

to detecting shilling behaviors and showed that how

the statistic data of a market would look like if

opportunistic behaviors do exist. They also showed

how to use an empirical model to test for

questionable behaviors (Kauffman and Wood, 2000).

However, their approach suffers from a few

problems, for example, it needs to review multiple

auctions over a long period of time (Gupta and

Bapna, 2002). Furthermore, the statistical approach

could not deal with the shilling problem directly.

In this paper, we propose to use model checking

technique to detect shilling behaviors in two

concurrent online auctions. Our approach can

directly detect shilling behaviors based on the latest

auction data, and then suggest shill suspects, if any.

The rest of this paper is organized as follows:

Section 2 introduces the pattern-based model

checking technique. Section 3 first presents a

motivation example for shill detection using model

checking. Then it introduces a model template and

shows how to build an auction model based on

auction data from two concurrent auctions. Section 4

provides a case study for how to use our approach to

detect shilling behaviors. Finally, in Section 5, we

provide conclusions and our future work.

2 PATTERN-BASED MODEL

CHECKING TECHNIQUE

2.1 The SPIN Model Checker

There is a wide variety of model checking tools

available, such as SPIN, NuSMV2, Java Pathfinder

and M

ARIA. Among them, the SPIN model checker

provides a friendly user interface and accepts model

specifications written in Promela (PROcess MEta

Language) (Holzmann, 1997). Promela is a CSP-like

language mainly used to describe abstract level

concurrent software system. Like any other

programming languages, Promela supports variables,

arrays and user-defined data types as well as control

flow statement. In addition, Promela supports

symbolic constants, message channels, processes,

selection and repetition, atomic sequence and

deterministic steps.

2.2 LTL and Patterns

The SPIN model checker supports specification of

system properties using Linear Temporal Logic

(LTL) (Pnueli, 1977), which is a formal method to

specify temporal relationships of statements. LTL

has been proven to have good expressivity and more

natural language like statements for verification.

LTL consists only a few logic operators, such as G

(always), F (eventually), U (until), W (unless, or

weak until) and O (next). Combining with Boolean

operators, i.e., && (and), || (or), ! (negation), →

(logical implication) and ↔ (logical equivalence),

LTL is capable of describing many key properties of

a concurrent software system.

On the other hand, like many other formal

specification and verification methods, writing a

LTL formula is not easy and error prone. Even a

person who has expertise in LTL may still have a

difficult time in understanding the semantic of a

LTL formula, such as

[]((Q&&!R&&<>R)→(P→

(!R U (S&&!R))) U R)

. To solve this problem,

Dwyer and his colleagues proposed a pattern-based

approach to helping software engineers to specify

requirements properties without having to worry

about the complexity and potential traps (Dwyer et

al., 1999).

There are quite a few patterns proposed in

previous work (Dwyer et al., 1999). Before we

present some of the patterns that we use in this

paper, we first introduce a notation called pattern

scope, which represents the extent of a program

execution over which the pattern must hold.

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

376

Global

Before

After

Between

and

After

until

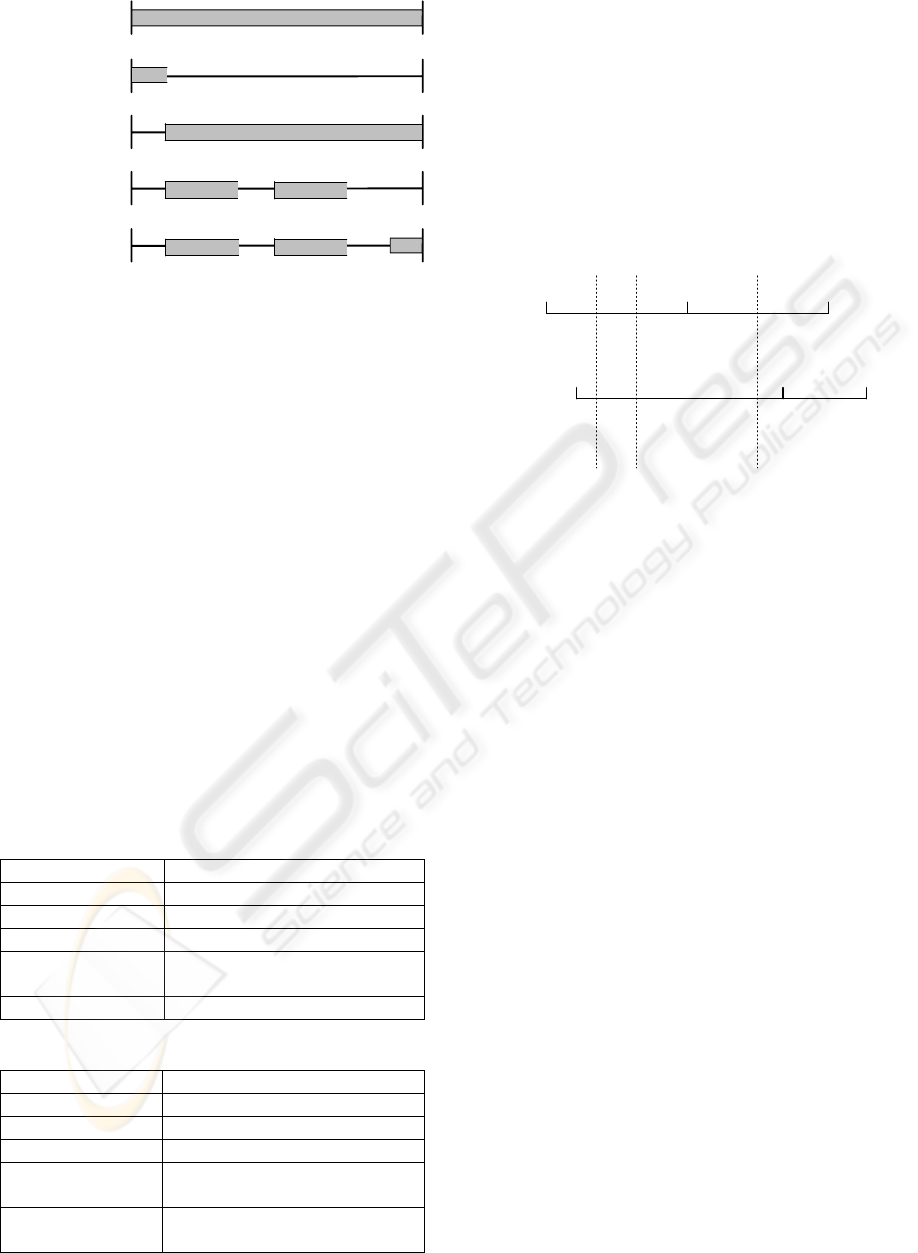
Figure 1: Pattern scopes for pattern-based LTL.

Figure 1 is an illustration of pattern scopes

adapted from (Dwyer et al., 1999). The capital

letters Q and R stand for events. Every pattern can

be assigned with one of the five scopes, in which

during the extent of the specified scope, a pattern

must hold. It should be clarified that all these pattern

scopes are defined as closed-left and open-right. For

example, if the scope is “Between Q and R”, then Q

is included in the scope but R is excluded.

In Table 1 and Table 2, we list two patterns that

are used in this paper. For example, the Absence

pattern in pattern scope “Before R” is described by

the formula

<>R → (!P U R). It specifies that

during the extent of the starting state and event R,

event P must be false. Similarly, the Existence

pattern in pattern scope “Between Q and R” is

described by the formula

[](Q && !R→(!R W (P

&& !R))), which specifies that during the extent of

event Q and event R, event P must become true.

For more LTL pattern definitions, please refer to

previous work (Dwyer et al., 1999).

Table 1: Absence patterns (event P is false).

Pattern Scope Formula

Globally [](!P)

Before R <>R → (!P U R)

After Q [](Q → [](!P))

Between Q and R []((Q && !R && <>R) →

(!P U R))

After Q until R [](Q && !R → (!P W R))

Table 2: Existence patterns (event P becomes true).

Pattern Scope Formula

Globally <>(P)

Before R !R W (P && !R)

After Q [](!Q) || <>(Q && <>P))

Between Q and R [](Q && !R→(!R W (P

!R)))

After Q until R [](Q && !R → (!R U (P

&& !R)))

3 MODELING CONCURRENT

ONLINE AUCTIONS

3.1 A Motivation Example

The basic idea of our approach is to automatically

generate an auction model based on auction data

from two concurrent auctions, and verify if the

auction model satisfies certain bidders’ behavioral

properties. The following figure (Figure 2) shows an

example of two concurrent auctions.

Auction 0

Auction 1

Start of Auction

Price is lower

User A bids

Price is lower

User A bids

Reach Reserve Price End of Auction

Start of Auction Reach Reserve Price End of Auction

TTT T

TTTTTTTT

Figure 2: An example of two concurrent auctions.

To simplify matters, we assume that the auction

that starts first is always Auction 0, and the one that

starts later is always Auction 1. In Figure 2, “T”

stands for “True”, and for each auction it has two

predicates, i.e., “Price is lower” and “User A bids”.

If any predicate becomes “T” at a certain point of

time in the process of any one of the two auctions, it

means that the event happens at that time. For

example, if “Price is lower” is “T” at a point in

Auction 0, it means that at that time, the bidding

price is lower in Auction 0. Similarly, if “User A

bids” is “T” at a point in Auction 1, it means that at

that time User A puts in his/her bid in Auction 1.

We use an example to show how to write a

pattern-based LTL formula for a certain behavioral

property. For instance, we want to detect the

following shilling behavior:

While two auctions are running concurrently, a

user bids in the auction that has higher bidding

price rather than lower bidding price.

Suppose Auction 0 starts first and also ends first.

Then we need to verify the following: after “start of

Auction 1” until “end of Auction 0”, does “(User A

bids in Auction 0 && price is lower in Auction 1) or

(User A bids in Auction 1 && price is lower in

Auction 0) become true?” The formula can be

composed using the Existence pattern with “After Q

until R” scope. If we use “S1” to represent “start of

Auction 1”, “E0” to represent “end of Auction 0”,

“P” to represent “User A bids in Auction 0 && price

is lower in Auction 1”, and “S” to represent “User A

bids in Auction 1 && price is lower in Auction 0”,

A FORMAL APPROACH TO DETECTING SHILLING BEHAVIORS IN CONCURRENT ONLINE AUCTIONS

377

the formula can be written as

([](S1 && !E0 ->

(!E0 U(P && !E0)))) || ([](S1 && !E0 ->

(!E0 U(S && !E0))))

From Figure 2, we can see that the behavior

specified above becomes true for three times

(denoted by three vertical dotted lines). Thus, the

LTL formula must be valid.

3.2 Preprocessing the Auction Data

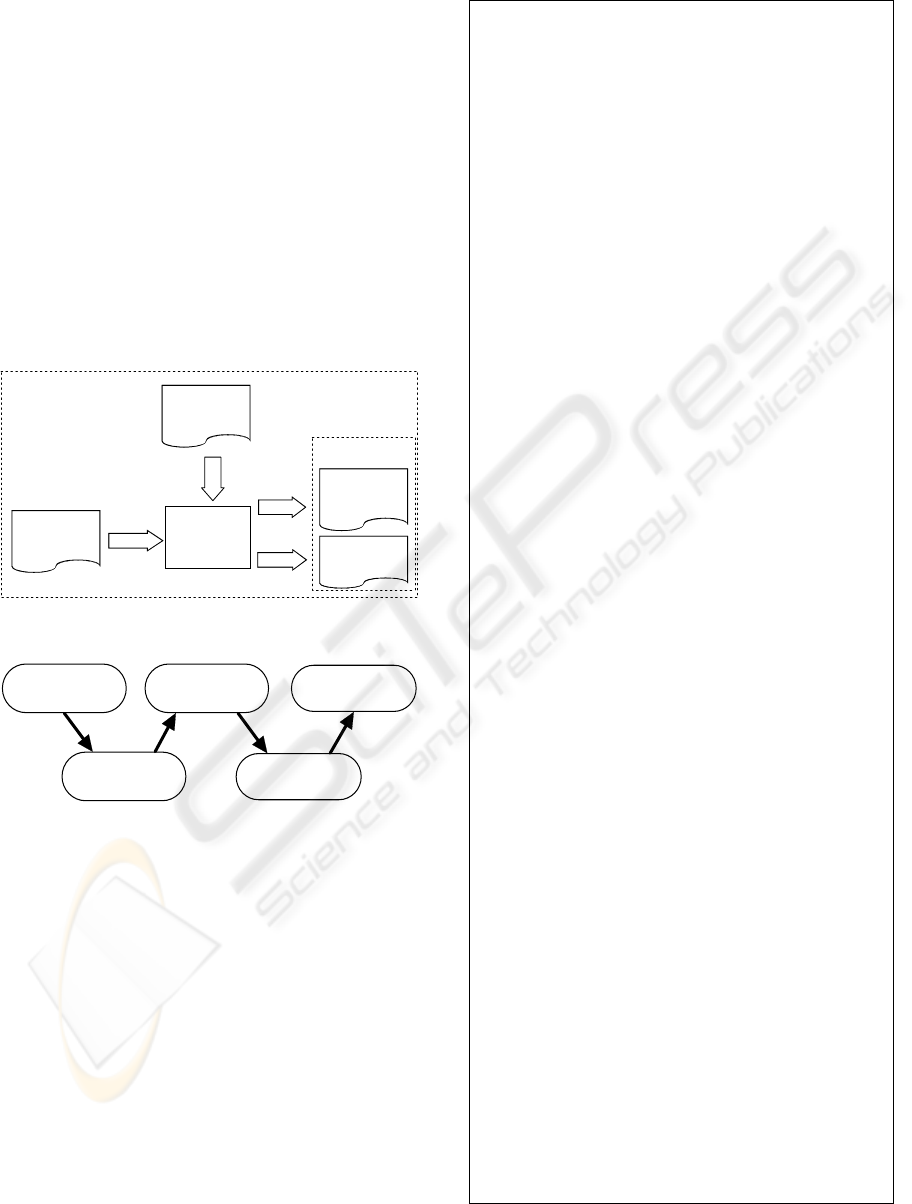
The first step to build an auction model is to

preprocess the auction data. As shown in Figure 3,

this task is accomplished by the Preprocessor, which

extracts numeric data from two concurrent auctions

and substitutes them into a model template to

produce a specific auction model.

Output

Input

Preprocess

Output

Preprocessor

Model Template

(template.txt)

Two Auctions

Data

Symbol

Definitions

(de finitions.txt)

Auction Model

Code (pan_in)

Model

Figure 3: Preprocessing the auction data.

Calculate Data Size

Code Generator

Parse User List

Re-arrange Data

Definition Generator

Figure 4: Preprocessor’s major tasks.

The generated auction model consists of a

Promela model code with an LTL symbol definition

file. The major sub-tasks in preprocessing of auction

data are illustrated in Figure 4, which consists of 5

steps, namely “Calculate Data Size”, “Parse User

List”, “Re-arrange Data”, “Generate Code”, and

“Generate Symbol Definitions”.

3.3 The Auction Model Template

The auction model template is written in Promela

code. The template allows us to generate different

Promela code for auction models based on different

extracted numeric auction data.

Table 3: Auction model template code.

int finalRound=…;

byte bidSeq[…];

byte flag0[…];

byte flag1[…];

int reservePrice0=…;

int reservePrice1=…;

int currentHighestBid0=…;

int currentHighestBid1=…;

int previousHighestBid0=…;

int previousHighestBid1=…;

int increment0[…];

int increment1[…];

typedef Auction{

int dataSize;

int timeInterval[…];

byte userIDs[…];

int bidAmount[…];

};

Auction auction0,auction1;

int timeElapse0, timeElapse1;

bit startPoint0=0;

bit startPoint1=0;

bit reservePoint0=0;

bit reservePoint1=0;

bit endPoint0=0;

bit endPoint1=0;

int roundCount=0;

proctype ModelChecker(){

checkingState:

::(roundCount < finalRound) ->

d_step{

startPoint0=0;

startPoint1=0;

reservePoint0=0;

reservePoint1=0;

endPoint0=0;

endPoint1=0;

::(bidSeq[roundCount]==0)->

::(flag0[roundCount]==1)->

startPoint0=1;

::(flag0[roundCount]==2)->

reservePoint0=1;

::else -> skip;

fi;

...

::(bidSeq[roundCount]==1)->

...

::(bidSeq[roundCount]==7)->

...

fi;

roundCount++;

}

:: else ->

goto endState;

od;

endState:

skip;

}

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

378

init{

bidSeq[0]=0;

...

auction0.dataSize=…;

auction0.agentIDs[0]=…;

auction0.bidAmount[0]=…;

auction0.timeInterval[0]=…;

...

flag0[0]=…;

...

run ModelChecker();

}

As shown in Table 3, we first define the global

variables in the auction template (line 1~19), which

will be initialized with values extracted from the

auction data in the

init procedure (line 67~78).

These global variables can be used to define symbols

to compose LTL formula. In line 20~28, we define

the local variables that can only be used by the

model checker.

The code between line 30-66 represents the state

transitions of the bidding process. When each

auction round starts, all flags are cleared (line

36~41). Then according to different bid sequences

that represent different bidding situations, the model

runs differently. For example, when the bid

sequence is “0”, it means that a bidder placed a bid

in Auction 0; while at the same time no one was

bidding in Auction 1. To handle this case, we first set

up the flags, and then all the old values from the

previous bid of the relevant variables are updated to

the new values that represent the current bid.

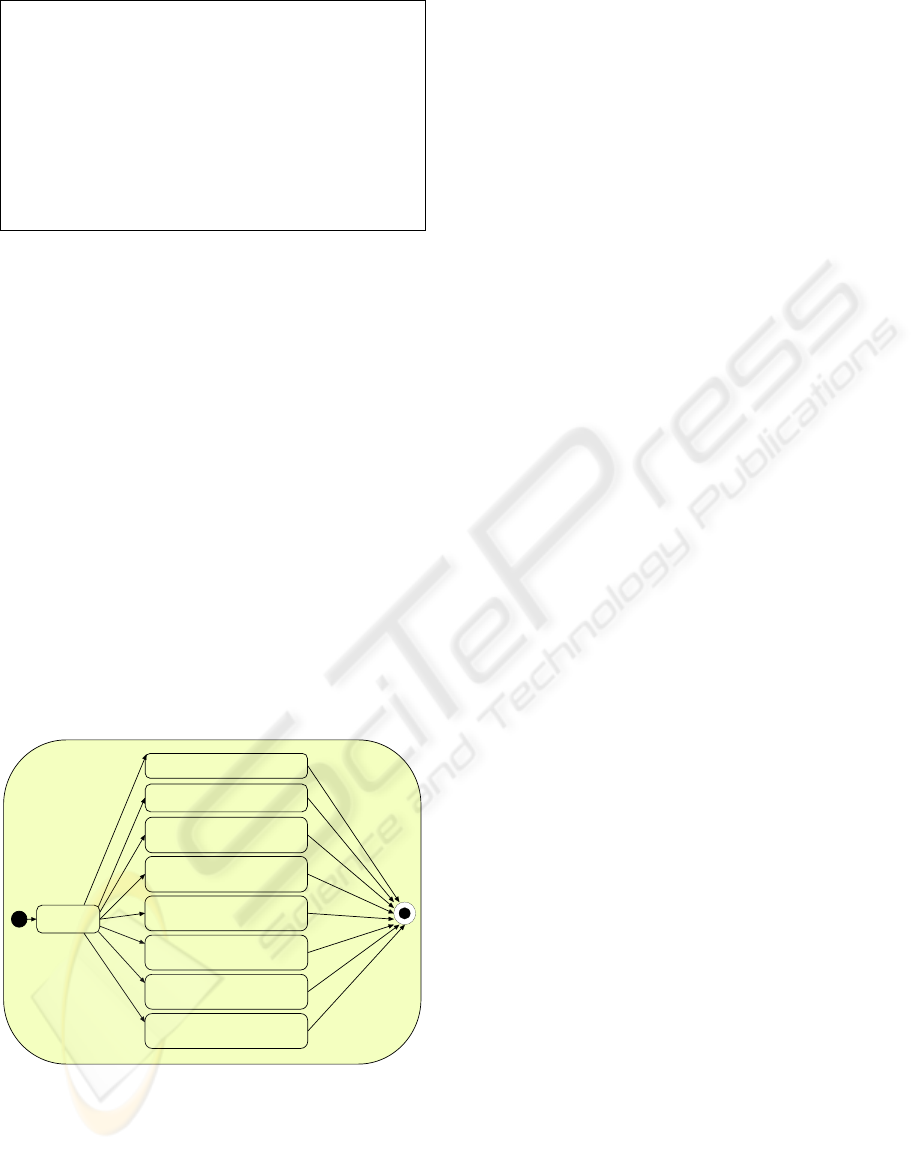
Clean A ll Flag s

Case 0: Auction 0 is bidding

Case 1: Auction 1 is bidding

Case 2: Both auctions are bidding at

the same time

Case 3: Auction 0 is bidding, and

Auction 1 has reached end of auction

Case 4: Auction 1 has reached end of

auction

Case 5: Auction 0 has reached end of

auction

Case 6: Auction 0 has reached end of

auction, and Auction 1 is bidding

Case 7: Both auctions have reached

end of auction at the same time

Figure 5: Different bidding situations.

In Figure 5, we show 8 different biding situations

in a UML state diagram that correspond to different

bidding sequences. Since each auction can be in one

of the following states: “bidding”, “not biding” and

“end”, we shall have 9 combinations for two

concurrent auctions. However, one of the cases (i.e.,

“not bidding, not bidding”) can be excluded from

consideration because when it happens, both

auctions must have already ended.

3.4 Symbol Definitions for LTL

In order to verify properties specified in LTL

formulas, we need to define symbols that can be

used in formula composition. We define most of the

terms to be self-explanatory. For example, “start0”

(“start1”) denotes the start of Auction 0 (Auction 1);

while “end0” (“end1”) denotes the end of Auction 0

(Auction 1). Similarly, the symbol “reserve0”

(“reserve1”) denotes that the reserve price of

Auction 0 (Auction 1) is reached. However, for a

term like “bid00”, the first “0” denotes Auction 0,

and the second “0” denotes the bidding behavior of

User 0. Thus, if a user numbered 16 bids on Auction

0, then it should be represented by the symbol

“bid016”.

Symbol definitions, combining with LTL

formulas, can ease the task of writing LTL formulas.

In practical use, users can also develop their own set

of symbol definitions.

3.5 The Model Checking Process

After the auction model has been created, the model

checking process becomes simple. The model

checking process consists of the following steps.

1. Duplicate the symbol definition file called

“definitions.txt” and name it as “pan.ltl”.

2. Type in the LTL formula. The formula will be

translated to “never claim” that can be used to

match either finite or infinite behaviors.

3. Append the generated “never claim” to the

“pan.ltl” file.

4. Use the SPIN to generate a model verifier (pan)

from both the Promela model code (“pan_in”)

and the file “pan.ltl”. The file “pan.ltl” should

contain both a “never claim” and symbol

definitions.

5. Compile the verifier source code (pan) using

“gcc” to produce an executable file “pan.exe”.

6. Execute the model verifier. After the execution

of the auction model, the model verifier will

show whether the result is valid or invalid. An

invalid result indicates that during the

verification process, the model verifier

encountered errors. If any errors are

encountered, the model we developed violates

the LTL formula that we specified. In this case,

the behavior we specified does not exist in the

model being checked.

A FORMAL APPROACH TO DETECTING SHILLING BEHAVIORS IN CONCURRENT ONLINE AUCTIONS

379

4 A CASE STUDY

In this section, we use a case study to show how

potential shills can be detected. The auction data was

collected from the eBay, but to protect users’

privacy, we have changed all user IDs (due to page

limitation, the auction data is not presented in this

paper). The titles for the two auctions are the same,

which is “HP/COMPAQ PRESARIO LAPTOP CD-

RW BURNER DVD WIRELESS”. Both auctions

are held by the same seller and the description to

these two auction items is shown in Table 4.

Table 4: Description of auctioned items.

Item Specifics - PC Laptops

Brand:

Compaq

Hard Drive Cap:

60 GB

Chip Type:

Screen Size:

15 inches

Model:

OS Included:

Yes

Processor

Speed:

1.4 GHz

Primary Drive:

CD-RW/DVD

Combo

Memory

512 MB

Condition:

To simplify our verification process, we have

made a few adjustments for the auction data. We

erased all currency symbols and time zone

abbreviations to make them appear simpler. We

rounded up all bidding prices that have decimals. In

addition, we added a user’s bidding price by 1 if the

user’s bidding price is the same as the previous bid.

Note that each user name is associated with a

numeric value in parentheses, which represents the

user’s feedback score.

Since the eBay does not provide any information

about the reserve price for each auction, as well as

whether the seller has set up a reserve price, we

assume the reserve prices for both auctions are $500.

The value of $500 is very close to both winning bids

($630 and $620), but sill gives us good ranges (from

$500 to $630 and from $500 to $620) for checking

bidding behaviors. We define overbid and deliberate

bid as follows.

Definition If the price difference between the

previous bid and the current bid is over 10 dollars, it

is considered as an overbid (a bid in large

increment).

Definition If the time gap between the current

bid and the previous bid is over 7200 seconds (2

hours), it is considered as a deliberate bid.

The reason we set 10 dollars as the boundary is

based on our observation, since most bid increments

are less than this number. Similarly, we set the 2

hours boundary for deliberate bid because 2 hours is

a reasonable period of time for a bidder to make a

deliberate decision. In practical, these two values

should be defined and adjusted according to auction

administrator’s experiences and observations.

In the two concurrent online auctions, there are

totally 35 users, among which we selected the

following four users for investigation: “paperchen”,

“benniten23”, “andy293” and “yass3d”. We chose

these four users because they are the only bidders

who are involved in both of the two concurrent

online auctions, and thus, they are more likely to be

shills.

After the auction data has been preprocessed, the

data is re-arranged. We then determine the auction

data’s overlapping style as shown in Figure 7.

Auction 0

Auction 1

Figure 7: Overlapping style for the two auctions.

We now use model checking techniques to verify

the following behavioral properties that are related

to shilling behaviors.

Property 1: User places a deliberate overbid before

R0 in Auction 0 or before R1 in Auction 1, but

doesn’t bid at all after R0 or R1.

Patterns Used: (1) Existence, before R (2) Absence,

after Q

Formulas:

For Auction 0:

((!reserve0 W ((action0) &&

!reserve0)))&&([](reserve0->

[](!action1

))) i.e., (((!reserve0 U

((action0

)&&!reserve0))||([]!reserve0))

)&&([](reserve0->[](!action1

)))

For Auction 1: ((!reserve1 W ((action0)&&

!reserve1)))&&([](reserve1->

[](!action1

))) i.e., (((!reserve1 U

((action0

)&&!reserve1))||([]!reserve1))

)&&([](reserve1->[](!action1

)))

Actions: For Auction 0: (overBid06 && deliBid0),

(overBid014 && deliBid0), (overBid016 &&

deliBid0) and (overBid017 && deliBid0) for

action0

; bid06, bid014, bid016 and bid017 for

action1. For Auction 1, the same rule applies.

Note: deliBid0 means the time interval between

currently placed bid and previous bid is longer than

the limit we have set, so the bid is considered as a

deliberate bid. The formula (overBid06 &&

deliBid0) means “paperchen” (numbered 6) is

placing a deliberate overbid.

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

380

Table 5: Model checking results for Property 1.

Auction

User

Auction 0 Auction 1

paperchen (5) Valid Valid

benniten23 (1) Invalid Invalid

andy293 (12) Invalid Invalid

yass3d (12) Invalid Invalid

Explanation: This property implies that a user

places an overbid to stimulate the bidding when he

notices that it has been a while since previous bid

was placed, and he stops bidding after the bid

reaches the reserve price. This behavior is highly

suspicious for shilling. From Table 5, we find that

only “paperchen” has such behavior, so he is very

likely a shill.

Property 2: After S1 until E0, user bids in auctions

that have higher bidding price.

Patterns Used: Existence, After Q until R

Formulas:

For Auction 0:

([](start1&&!end0->(!end0 U

((action

)&&!end0))))

For Auction 1: ([](start1&&!end0->(!end0 U

((action

)&&!end0))))

Actions: (bid06 && p1Lower), (bid014 &&

p1Lower), (bid016 && p1Lower), (bid017 &&

p1Lower) for Auction 0. The same rule applies to

Auction 1.

Note: The variable p1Lower means the bidding

price in Auction 1 is lower than that in Auction 0. So

(bid06&&p1Lower) means “paperchen” is bidding

on Auction 0 when Auction 1 has lower bidding

price.

Table 6: Model checking results for Property 2.

Auction

User

Auction 0 Auction 1

paperchen (5) Invalid Valid

benniten23 (1) Valid Valid

andy293 (12) Valid Invalid

yass3d (12) Valid Invalid

Explanation: Since during the time the two auctions

overlap, anyone who doesn’t bid on the auction that

has the cheaper bidding price is suspicious. From

Table 6, we notice that the results for the user

“benniten23” were valid for both auctions, which

suggest that the user might not be a normal bidder.

Based on the above analysis, we can conclude

that the user “paperchen” and “benniten23” are

possible shills because both of them attempted to

drive up the bidding price and one of them

(“paperchen”) stopped bidding after the price

reached the reserve price. When a certain amount of

time has passed after the last bid, “paperchen” tried

to create a competitive bidding atmosphere by

placing overbids. Notice that our approach can

effectively detect and suggest shill suspects;

however, it is not guaranteed that suspects must be

shills. Based on the model checking results, we can

easily track the suspects’ bidding history and draw

conclusions if the suspects are actually shills.

5 CONCLUSIONS AND FUTURE

WORK

In this paper, we introduced a model checking

approach to detecting shilling behaviors in

concurrent online auctions. We proposed an auction

model template that supports automatic generation

of auction models based on auction data. With our

pattern-based model checking approach, we can not

only easily write specifications for bidding

behaviors, but also directly detect suspicious shills in

concurrent online auctions. Our approach can be

easily extended to support more than two concurrent

online auctions. To provide tool support for

automatic generation of specifications of shilling

behaviors envisions our future research work.

REFERENCES

Dwyer, M. B., Avrunin, G. S., and Corbett, J. C., 1999.

Patterns in property specifications for finite-state

verification. In Proceedings of the 21st International

Conference on Software Engineering (ICSE 99), Los

Angeles, pp. 16-22.

Gupta, A. and Bapna, R., 2002. Online mercantile

processes: a closer look at B2C online auctions. In

Handbook of Electronic Commerce in Business and

Society, P. B. Lowry, R. J. Watson, and J. O.

Cherrington eds., St. Lucie Press, pp. 85-98.

Holzmann, G. J., 1997. The model checker SPIN. IEEE

Transactions on Software Engineering, Volume 23,

No. 5, pp. 279-295.

Kauffman, R. J., and Wood, C. A., 2000. Running up the

bid: modeling seller opportunism in Internet auctions.

In Proceedings of the Sixth Americas Conference on

Information Systems (AMCIS 2000), M. Chung (ed.),

Long Beach, CA, pp. 929-935.

Pnueli, A., 1977. The temporal logic of programs. In

Proceedings of the 18th IEEE Symposium on

Foundations of Computer Science, IEEE Computer

Society Press, pp. 46-67.

Wang, W., Zoltán, H., and Whinston, A. B., 2002. Shill

bidding in multi-round online auctions. In Proceedings

of the 35th Hawaii International Conference on

System Sciences (HICSS’02), Hawaii, USA.

A FORMAL APPROACH TO DETECTING SHILLING BEHAVIORS IN CONCURRENT ONLINE AUCTIONS

381