
USING SHADOW PRICES FOR RESOURCE ALLOCATION IN A
COMBINATORIAL GRID WITH PROXY-BIDDING AGENTS
Michael Schwind
Institute of Information Systems, J. W. Goethe University
Mertonstrasse 17, D-60054 Frankfurt, Germany
Oleg Gujo
Institute of Information Systems, J. W. Goethe University
Mertonstrasse 17, D-60054 Frankfurt, Germany
Keywords:
Resource allocation, combinatorial auction, grid computing, agent-oriented programming.
Abstract:
Our paper presents an agent-based simulation environment for task scheduling in a distributed computer sys-
tems (grid). The scheduler enables the simultaneous allocation of resources like CPU time, communication
bandwidth, volatile, and non-volatile memory while employing a combinatorial resource allocation mecha-
nism. The resources are allocated by an iterative combinatorial auction with proxy-bidding agents that try to
acquire their desired resource allocation profiles with respect to limited monetary budget endowments. In order
to achieve an efficient bidding process, the auctioneer provides information on resource prices to the bidding
agents. The calculation of explicit resource prices in a combinatorial auction is computationally demanding,
especially if the the bid bundles exhibit complementarities or substitutionalities. We therefore propose a new
approximate pricing mechanism using shadow prices from a linear programming formulation for this purpose.
The efficiency of the shadow price-based allocation mechanism is tested in the context of a closed loop grid
system in which the agents can use monetary units rewarded for the resources they provide to the system
for the acquisition of complementary capacity. Two types of proxy-bidding agents are compared in terms of
efficiency (received units of resources, time until bid acceptance) within this scenario: An aggressive bidding
agent with strongly rising bids and a smooth bidding agent with slowly increasing bids.
1 INTRODUCTION
We present an agent-based simulation environment
for resource allocation in a distributed computer sys-
tem that employs shadow prices as an information en-
tity to optimize the allocation process. Our environ-
ment allows the simulation of a mechanism for the
simultaneous allocation of resources like CPU time,
communication bandwidth, volatile and non-volatile
memory in the distributed computer system. In con-
trast to traditional grid allocation approaches, our al-
location process considers production complementar-
ities and substitutionalities for these resources making
the resulting resource usage much more efficient. The
central scheduling instance of our system is compara-
ble to an auctioneer that performs an iterative com-
binatorial auction in which proxy-agents try to ac-
quire the resources needed in computational tasks for
the provision of information services and informa-
tion production (ISIP)
1
by submitting package bids
1
Examples for ISIP tasks are e.g. the provision of Web
services, the customized retrieval and replication of cus-
for the resource combinations. The proxy-agents’
willingness-to-pay (W2P) for these bundles is con-
straint by limited budgets of a virtual currency they
are endowed with. The allocation system simulates a
closed-loop grid economy in which the agents gain
monetary units for resources they provide to other
grid system participants via auctioneer. The earned
virtual currency can be used for the acquisition of
complementary resource capacity by submitting com-
binatorial bids. The simulation environment allows
the utilization and benchmarking of different proxy-
bidding strategies in various system load situations.
Two main bidding strategies are compared in this pa-
per:
• An aggressive bidding agent that submits combina-
torial bids while trying to achieve quick bid accep-
tance by using a fast inclining bid pricing strategy.
• A smooth bidding agent that submits multiple bid
bundles to the auctioneer waiting for bid accep-
tance of some of the alternative bids while increas-
tomized stock chart data or the broadcast of a public event
to viewers via TCP/IP protocol.
11
Schwind M. and Gujo O. (2006).
USING SHADOW PRICES FOR RESOURCE ALLOCATION IN A COMBINATORIAL GRID WITH PROXY-BIDDING AGENTS.
In Proceedings of the Eighth Inter national Conference on Enterprise Information Systems - SAIC, pages 11-18
DOI: 10.5220/0002461500110018
Copyright
c
SciTePress

ing the bid prices only slowly.
The bidding strategies are compared with each
other regarding their allocation-related efficiency,
which is measured in terms of received resource units
per virtual currency unit spent by the agents and in
terms of time to bid acceptance in the auction process.
2 COMBINATORIAL AUCTIONS
FOR RESOURCE ALLOCATION
IN DISTRIBUTED COMPUTER
SYSTEMS
Various auction protocols have been proposed for re-
source allocation in distributed computer systems in
the last decades. The transfer of economic principles
to resource attribution in grid systems, like the price
controlled resource allocation (PCRA)
2
used in our
scenario, allows flexible implementation of allocation
mechanisms in decentralized systems (Buyya et al.,
2001).
Combinatorial auctions are a suitable tool to allo-
cate interdependent resources because they can take
their substitutionalities and complementarities into
account. The production process for information ser-
vices in distributed systems comprises an allocation
problem with strong complementarities. For exam-
ple, if an information service such as the provisioning
of a video conference service via the web or the off-
line calculation of distributed database jobs has to be
processed on different computers and acquires CPU
time without obtaining communication network ca-
pacity between the computers at the same time, the
acquired CPU time is worthless. The application of
combinatorial auctions for resource allocation in dis-
tributed computer systems is still in its infancy despite
its excellent applicability to grid computing. A com-
binatorial auction-based mechanism for resource allo-
cation in a SensorNet testbed was presented by (Chun
et al., 2004) in a recent approach. The devices in
this mechanism feature different capabilities in vari-
ous combinations. The periodically performed com-
binatorial sealed-bid auction is implemented within
the microeconomic resource allocation system (MI-
RAGE). The system uses a very simple combinatorial
allocation mechanism to achieve sufficient real time
performance. MIRAGE users have accounts based on
a virtual currency enabling a bartering process for the
SensorNet resources. A consequent continuation of
this work is the grid computing environment Bella-
gio by (AuYoung et al., 2004). Each bidder has a
budget of a virtual currency available for task pay-
2
The price is used as a control variable for the schedul-
ing mechanism, requests with higher W2P are prioritized.
ment purposes. The assignment of the required re-
sources to the particular tasks is done by a combi-
natorial second-price auction, which comes close to
a strategy proof mechanism. In several experiments,
the system is tested for scalability, efficiency, and fair-
ness. Due to the simple greedy algorithm used in this
system, the efficiency of the resulting resource alloca-
tion is not satisfying.
3 AN AGENT-BASED
SIMULATION ENVIRONMENT
FOR COMBINATORIAL
RESOURCE ALLOCATION
Our combinatorial grid scheduling environment, real-
ized in JADE 3.3, goes beyond the recent approaches
in several points:
• The system allows the usage of several winner de-
termination algorithms like simulated annealing,
genetic programming, and integer programming
methods according to the users’ requirements in
terms of allocation quality and computation time
3
.
• The simulator provides tools to investigate various
bidding behaviors of the proxy agents in the re-
sources acquisition process. We will concentrate
on this aspect in this paper.
• The framework can simulate changing resource ca-
pacities to test the combinatorial grid scheduler’s
response with respect to allocation efficiency and
system stability.
3.1 Scenario for a PCRA in a
Combinatorial Grid Scheduler
This section gives a brief overview on the resource al-
location scenario for ISIP provision used in our work.
The scenario includes four resource types:
• Central processing units (CPU) that are mainly re-
sponsible for the data processing in the ISIP tasks.
• Volatile memory capacity (MEM) which is neces-
sary to store short-term processing data for the cen-
tral processing units.
• Non-volatile storage capacity (DSK) which is nec-
essary to keep mass data on databases and to pro-
vide program codes for the execution of the ISIP
processes.
3
For algorithm description see (Schwind et al., 2003).
ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING
12
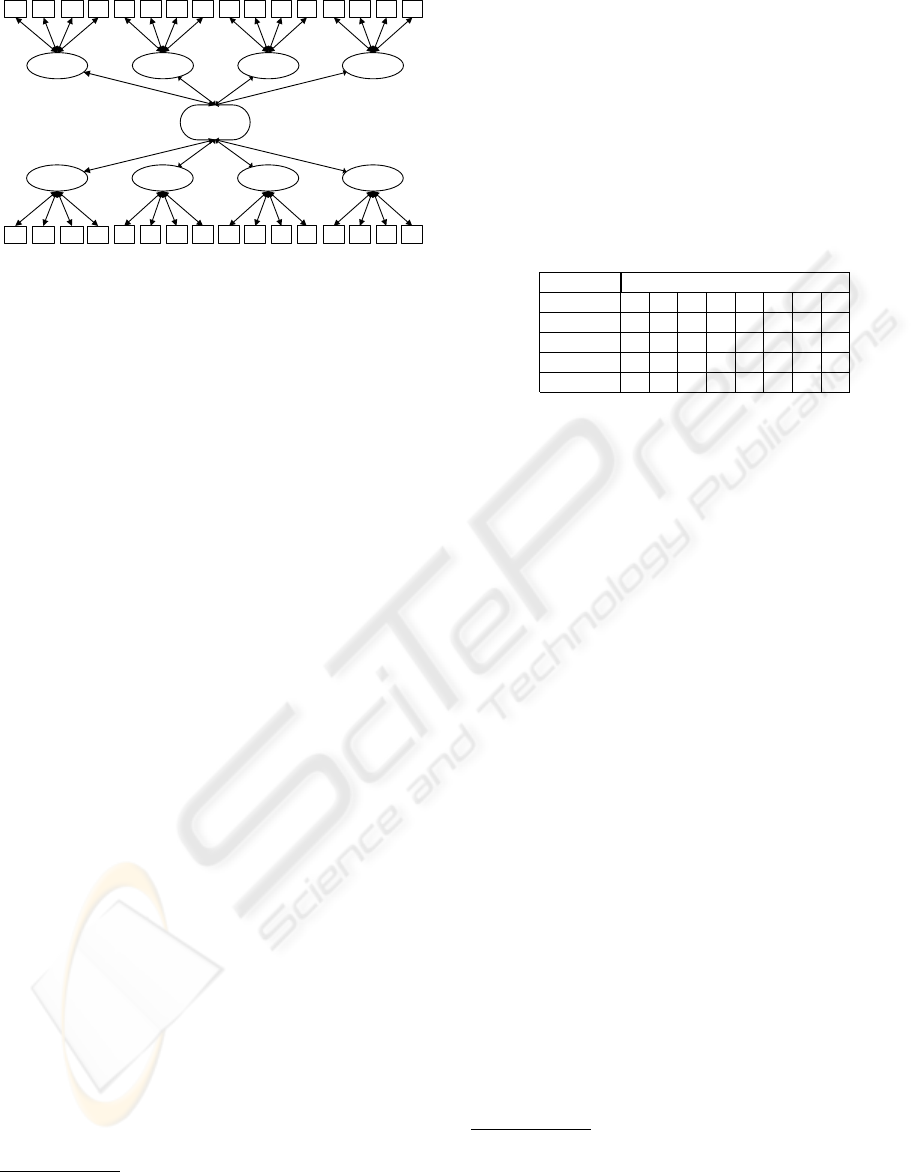
(Distributed-)
Market
Mediator(s)
Task
Agent 1
Task
Agent 4
Task
Agent 3
Task
Agent 2
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
Resource
Agent 1
Resource
Agent 4
Resource
Agent 3
Resource
Agent 2
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
MEM
CPU
NET
DSK
Figure 1: Scenario for the allocation of ISIP resources.
• Network bandwidth (NET) that is required for data
interchange among the grid computer units
4
.
The general PCRA scenario used within the com-
binatorial grid simulator is constructed as follows:
• Task agents (bidders) are engaged in acquiring the
resources needed to process the ISIP task in the dis-
tributed computer system on behalf of real world
clients. They do this by bidding for the required
resource combination via the mediating agent.
• A mediating agent (auctioneer) receives the re-
source bids and calculates an allocation profile for
the available resources managed by the resource
agents according to the allocation mechanism. Af-
ter a successful auction process, bidders are in-
formed about the acceptance of their bids.
• Resource agents collect information about avail-
able resources on their particular host IT systems
through a network of distributed computers and
provide this information to the market mediator.
The resource agents offer the available capacities to
the task agents via the mediating agent. If a bid is
accepted via the auctioneer, the acquired resources
are reserved for the corresponding winning agent
in advance.
Figure 1 depicts the ISIP allocation scenario. Re-
source agents administrate available MEM, CPU,
NET, and DSK capacities on their particular host
computers systems on the supply side. On the de-
mand side, task agents collect the required resource
combinations including MEM, CPU, NET, and DSK
capacity needed to accomplish their production tasks.
Between resource and task agents, there is a mar-
ket mediator that allocates the resources employing
a combinatorial auction. For the formal representa-
tion of the bids, a two-dimensional bid-matrix (BM)
4
Network connections themselves exhibit complemen-
tarities due to their peering character. For simplicity rea-
sons, we assume that NET capacity can be managed as one
single system resource.
is used. One dimension of the BM describes the
time t ∈{1,...,T} at which the resource is required
within the request period T
5
. The other dimension
r ∈{1,...,R} denotes the resource types MEM,
CPU, NET, DSK. The request for a quantity of an in-
dividual resource r at time t is then denoted by a ma-
trix element q(r, t). A price p is assigned to each BM
expressing the agent’s W2P for the resource bundle.
Table 1: Example for a structured bid matrix BM submitted
by a task agent.
BM
struc.
Time Slot t
Resources 1 2 3 4 5 6 7 8
r
1
2 2 3 3 3
r
2
1 1 1
r
3
2 2 1 1 1 1
r
4
3 3 2 2
In addition to the BM , two other matrix types play
an important role within our grid simulation frame-
work:
• The allocation matrix (AM) describes the awarded
allocation q(r, t) for resources r and time slots t
within the following ISIP provision period T .
• The constraint matrix (CM) expresses the maxi-
mum quantity q
max
(r, t) of resource r the auction-
eer can assign to the task agents at time t. The max-
imum possible resource load of the CM represents
the aggregated resource availability for the follow-
ing time slots.
q
bmax
denotes the maximum resource load that can
be requested by a bidder for a single BM element
q
i,j
(r, t). In our matrix instances each entry in a BM
is occupied with probability p
tso
.
3.2 The Combinatorial Scheduling
Auction
In the following paragraph, the course of the com-
binatorial grid auction is described in the light of an
UML sequence diagram based on the FIPA definition
of the English auction (steps are denoted in )
6
:
1. The auctioneer requests the resource agents to eval-
uate the available resource capacities and informs
the bidders about the bidding terms. Then he an-
nounces the start of the auction. Additionally,
the auctioneer awards an initial budget to the task
agents.
5
Time period T is divided into equidistant intervals
(time slots t) within the simulation model. The time pe-
riod T is identical to a following production time span t
pro
at which the ISIP provision takes place.
6
See foundation for intelligent physical agents www.
fipa.org/specifications/fipa00031D.
USING SHADOW PRICES FOR RESOURCE ALLOCATION IN A COMBINATORIAL GRID WITH
PROXY-BIDDING AGENTS
13

2. Following the auctioneer’s call-for-proposal, the
task agents create their bids according to the de-
sired resource combination. Bidders compute the
associated bid price dependent on their actual pric-
ing policy, their budget level, and the latest re-
source prices.
3. The auctioneer receives the bids and calculates the
return-maximizing combinatorial allocation. He
informs the task agents about any bid accep-
tance/rejection and requests the resource agents to
reserve the awarded resources.
4. Resource agents inform the auctioneer about the
status of the task execution.
5. The auctioneer propagates any task status informa-
tion to the task agents, and the agents’ accounts
are debited with the bid prices of the awarded bids.
Then a call-for-proposal for the next round is is-
sued.
6. Task agents can renew their bids in the next round
in case of non-acceptance or non-execution. The
agents’ bid pricing follows rules defined in the sub-
sequent paragraph.
7. The process is repeated until the auctioneer an-
nounces the end of the auction.
In the following, the three crucial elements of the
combinatorial grid scheduling system are described in
more detail: the budget management mechanism, the
combinatorial auctioneer, and the task agents’ bidding
behavior.
3.2.1 The System’s Budget Management
Mechanism
Each of the task agents a
i
holds a monetary budget
BG
i
that is initialized with a fixed amount BG
ini
of
monetary units (MUs) at the start of the system. At
the beginning of each round k, the task agents’ bud-
gets are refreshed (see figure 2, 1) with an amount
of MUs enabling them to acquire the resource bun-
dles b
i,j
required for their ISIP provision task. The
agents’ budget refill can be done in two ways in our
grid economy:
• A fixed amount BG
inc
that is defined by the system
user is added to the agents’ budgets independently
of the production capacity they provide to the grid
system. This case, where task agents only behave
as consumers, is denoted as an open grid econ-
omy. The resource agents which own the resources
act independently from the task agents providing
only resource availability and resource usage in-
formation to the auctioneer. The resource agents
are compensated by the auctioneer for the capacity
provided proportionately to the auctioneers income
Inc
acc
.
auctioneer
resource agent
request-resource-info 1
provide-resource-info
X
X
not-understood (m>0)
task agent
inform-start-of-auction
initAuction ()
n1
n
1
n
call-for-proposal 1
computeBidPrice ()
createBids ()
X
not-understood (m>0)
propose
computeAllocation ()
computeResourceCap ()
request-resource
bookResource ()
executeTask ()
inform-task-execution
X
not-understood / task-failure (m>0)
l
nl
n
m
l
m
l
l
m
n
l
l
l
X
reject-proposal
accept-proposal
l
X
inform-end-of-auction
call-for-proposal 2
n
n
initBudget ()
refreshBudget ()
debitBidPrice ()
request-resource-info 2
n
1
2
3
5
7
4
6
Figure 2: FIPA AUML diagram for the iterative combinato-
rial scheduling auction.
• Task and resource agents act as a unit of consumer
and producer both owning the resources of their
peer system. This means a task and a resource
agent reside simultaneously on each peer computer
in the grid. The resource agent does the reporting of
resource usage and provisioning for the task agent
owning the peer computer resources (see figure 2,
1,4)
7
. The agents on the peer computer are com-
pensated for the resources provided to the system.
The compensation process is organized by the auc-
tioneer. Starting with the initial budgets BG
ini
the
amount of MUs circulating in the system is kept
constant for the closed grid economy.
The accounting of the agents’ budgets in the grid sys-
tem is done by the combinatorial auctioneer (see fig-
ure 2, 1,5).
3.2.2 The Combinatorial Auctioneer
The combinatorial auctioneer controls the iterative al-
location process of the grid system. For this purpose,
the auctioneer awaits the XOR-bundled bids b
i,j
that
have been submitted by the task agents a
i
for the cur-
rent round. The bids that are submitted in the form
of BM s are shown in Table 1. They represent the
task agents requests for resource capacity q
i,j
(r, t) at
7
In Figure 1 this implies that resource agent 1 and task
agent 1 reside on the same peer computer.
ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING
14

a particular point of time t. After having received
all alternative BM s submitted by the task agents,
the auctioneer has to solve the combinatorial auc-
tion problem (CAP) which is NP-hard (Parkes and
Ungar, 2000; Fujishima et al., 1999). The CAP is
often denoted as the winner determination problem
(WDP), according to the traditional auctioneers task
of identifying the winner. The formal description of
the CAP could be considered as a special variant of
the weighted set packing problem (WSPP) (Vries and
Vohra, 2001) and is formulated as:
max
I
i=1
J
j=1
p
i,j
x
i,j
subject to
I
i=1
J
j=1
q
i,j
(r, t) x
i,j
≤ q
max
(r, t),
where r ∈{1,...,R},t∈{1,...,T} and
J
j=1
x
i,j
≤ 1, where i ∈{1,...,I}.
(1)
Resources: r ∈ N
Time slots: t ∈ N
Resource requests: q
i,j
(r, t) ∈ N
Price for bid b
i,j
: p
i,j
∈ R
+
Acceptance variable: x
i,j
∈{0,1}
Bid j of agent i: b
i,j
∈ B
Income for all accepted bids: Inc
acc
∈ R
+
The goal is to maximize the auctioneers income.
q
max
(r, t) is the maximum capacity of resources at
time t available to the auctioneer and B is the set of
all bids b
i,j
. Furthermore, we refer to the set of ac-
cepted bids as I
+
(with I
+
⊆ B).
3.2.3 Shadow Price Calculation
For an efficient bidding process it is necessary to pro-
vide preferably exact information about the actual
auctioneer’s valuation of the resources to the proxy-
agents. However, it is not possible to calculate unam-
biguous prices (anonymous prices) for the individual
resources in a combinatorial auction due to the non-
linearities in the bidders’ valuations (Xia et al., 2004).
In many cases, explicit resource prices can only be
calculated for each individual bid. (Kwasnica et al.,
2005) describes a pricing scheme for all individual
goods in a combinatorial auction by approximating
the prices in a divisible case based on a linear pro-
gramming (LP) approach first proposed by (Rassenti
et al., 1982). Like in a similar approach by (Bjørndal
and Jørnsten, 2001), they use the dual solution of the
relaxed WDP which is used to calculate the shadow
prices (SP). In our simulation model we adopt the
dual LP approach of (Kwasnica et al., 2005) including
accepted bids as well as rejected bids
8
:
min z =
r t
q
max
(r, t) · sp
r,t
(2)
subject to
r t
q
i,j
(r, t) · sp
r,t
= p
i,j
∀b
i,j
∈ I
+
(3)
r t
q
i,j
(r, t) · sp
r,t
+ δ
i,j
≥ p
i,j
∀b
i,j
∈ I
−
(4)
Accepted bid set: I
+
⊆ B
Rejected bid set: I
−
⊆ B
Reduced cost: δ
i,j
∈ R
+
0
Shadow price acceptance: sp
r,t
∈ R
+
0
We use the primal solution of the LP problem deliv-
ered from open source LP solver LPSOLVE 5.5
9
to the
appointment of sets I
+
and I
−
. As described above,
our matrix has R × T elements, i.e. for every resource
r ∈ R there are T time slots. We group the results as
follows:
SP
r
(k)=
T
t=1
sp
r,t
∀r ∈ R (5)
Shadow price: SP
r
(k) ∈ R
+
0
In general bid prices are not assumed to be linear in
our framework. This means that shadow prices SP
cannot be calculated by the auctioneer for each round,
i.e. there is no solution to the LP problem, or reduced
costs equal to zero for a number of bids (Bjørndal and
Jørnsten, 2001). In such cases we rely on an approx-
imate shadow price calculation based on pricing his-
tory (H
sp
)
10
:
SP
r
(k)=
h
sp
|H
sp
|
∀h
sp
∈ H
sp
(6)
h
sp
=
SP
r
(k) if SP
r
(k) =0 ∧ k =1
0 if k =1
(7)
Now we can investigate the market value of a resource
unit while we use the shadow prices and form the
sums of each resource r ∈ R and each time slot t ∈ T
for all accepted bids:
8
The result of the following formula is denoted as re-
duced shadow prices. By omitting the rejected bids in
the calculation of dual prices, the result would be higher
(Bjørndal and Jørnsten, 2001).
9
http://www.geocities.com/lpsolve/
10
(Xia et al., 2004) propose an iterative price adaption
process for those cases to achieve an approximate solution
anyway. Due to time criticality of our system we stick to
the pricing history solution.
USING SHADOW PRICES FOR RESOURCE ALLOCATION IN A COMBINATORIAL GRID WITH
PROXY-BIDDING AGENTS
15

v
r
(k)=
SP
r
(k)
t
i j
q
i,j
(r,t)
∀b
i,j
∈ I
+
if I
+
=0
∧ SP
r
(k) =0,
h
sp
t
i j
q
i,j
(r,t)
∀b
i,j
∈ I
+
if I
+
=0,
0 otherwise
(8)
Market value of a resource unit: v
r
(k) ∈ R
+
0
3.2.4 The Task Agents’ Bidding Model
The task agents’ bidding behavior is determined by
two factors:
• At each round, o new bids b
i,j
are generated for
each task agent a
i
. The structure of the new gen-
erated BM s varies according to the matrix types
defined in section 3.1. The proxy-agents a
i
have
the possibility to submit bids b
i,j
as exclusively el-
igible bundles. The eligibility is defined such that
mBMsare treated as XOR bids
11
.
• Task agents repeat bidding for rejected bids in the
following round while changing the W2P with re-
spect to the actual resource supply/demand situa-
tion.
In our simulation environment we use different
types of new BM s generated by the task agents
12
.
The BM s used in this paper have a structured pat-
tern: bidder agents require resources with the same
intensity for a longer period of time (up to t
max
slots).
This results in continuous bids of varying lengths that
are close to realistic demand structures in distributed
ISIP systems.
Based on the resource occupancy q
i,j
(r, t) in
the BM s that are requested by the ISIP provision
process, the proxy-agents have to formulate their as-
sociated W2P for the bids. Two cases have to be dis-
tinguished (see equation 10):
• In the first round, no estimation of the prices can
be given to the bidders. For this reason, bidders
formulate the W2P for their first bids with respect
to the initial budget BG
i
and their bidding strategy.
This is done by calculating a mean bid price that
guarantees the proxy bidder’s budget to last for the
next l rounds if o bids are added in each round.
• In the following rounds, the task agents’ calculate
their W2P for the new submitted bids employing
market values for the resources given in equation
8. A factor P
ini
i
is included into the calculation of
11
For the definition of OR, XOR, and other variants
of bid connections within bidding languages see (Nisan,
2005).
12
See (Schwind et al., 2003) for the BM type definitions.
the initial bids. By setting P
ini
i
to e.g. 0.8, task
agents are prompted to submit initial bids slightly
lower than resource market price or above market
level for e.g. P
ini
i
=1.2. For the rejected bids,
task agents show the following behavior. The ac-
tual price for a bid b
i,j
of task agent a
i
in the actual
round of a bid is calculated by using the market val-
ues of the resources derived from the shadow prices
of the preceding round. In order to control the price
adaption process, a price acceleration factor ∆P is
introduced rising P
inc
i
by multiplying ∆P with the
actual number of rounds of the particular bid b
i,j
:
P
inc
i
= P
ini
i
+(round of bid · ∆P ) (9)
The bidding for rejected bids is repeated for the
following production time span t
pro
for the next l
rounds until the bid is accepted, otherwise the bids
are discarded. The agents bidding behavior is lim-
ited by the task agents’ budget. If the agents budget
is exhausted, no further bids are formulated until
the budget is refreshed in the next round k.
p
i,j
(k)=
BG
i
l·o
for k =1
S
r=1
N
t=1
v
r
(k − 1) · q
i,j
(r, t) · P
inc
i
for k>1
(10)
The bidding behavior of the task agents can be
modified by varying parameters like ∆P, o, l and m.
4 TESTING DIFFERENT
BIDDING STRATEGIES
In this section we will have a closer look at two differ-
ent economically motivated bidding strategies defined
by the task agents’ parameters described above. The
bidding strategies evaluated in this paper only differ
in ∆P:
• An aggressive bidding agent that submits combi-
natorial bids while trying to achieve the bid accep-
tance by using a fast inclining bid pricing strategy.
The economic motivation of this behavior can be
a proxy agent that bids for the execution of time
critical tasks in an ISIP provisioning system. A
good example of this is the performance of a video
conference in the distributed system. The confer-
ence is scheduled for a narrow time window. The
proxy agents have to bid for a prompt fulfillment
of the resource usage tasks. Therefore, it is useful
that proxy agents quickly raise their bids to market
level.
ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING
16
0,50 1,00 1,50
delta price increment
1,00
1,25
1,50
1,75
2,00
a
c
c
e
p
t
a
n
c
e
t
i
m
e
a
g
e
n
t
2
0,50 1,00 1,50
delta price increment
1,00
1,25
1,50
1,75
2,00
a
c
c
e
p
t
a
n
c
e
t
i
m
e
a
g
e
n
t
1
delta price increment
1,30,90,50,10
mean round time
2,0
1,8
1,5
1,3
1,0
0,50 1,00 1, 50
delta price increment
1,00
1,25
1,50
1,75
2,00
p
r
i
c
e
p
e
r
u
n
i
t
r
e
s
o
u
r
c
e
2
0,50 1,00 1, 50
delta price increment
1,00
1,25
1,50
1,75
2,00
p
r
i
c
e
p
e
r
u
n
i
t
r
e
s
o
u
r
c
e
1
delta
p
rice increment
1,30,90,50,10
mean resour ce price
2,0
1,8
1,6
1,4
1,2
1,0
,8
Figure 3: Mean round time (up) and price per resource unit (below) for smooth (agent 2) and aggressive bidder (agent 1) in
dependency of price increment ∆P .
• A smooth bidding agent that submits multiple bid
bundles to the auctioneer waiting for bid accep-
tance of some of the alternative bids while increas-
ing the bid prices slowly. The economic rationale
for this type of proxy agent strategy can be the fact
that it bids for resources required for the fulfillment
of an ISIP task that is not time-critical. An exam-
ple of this may be the computation of large time-
consuming database jobs on a distributed system
that have to be done in a very relaxed time win-
dow. A plausible strategy for the proxy bidding
task agent is then to try to acquire the required re-
source capacity bundles at low market values with
bids with slightly increasing W2P.
For construction of the closed-loop grid economy
in our experiments we assumed the same produc-
tion function for all task agents leading to equal
payoff Inc
acc
/I of the auctioneer’s income Inc
acc
(BG
ini
= 200MUs). The applied strategy was either
increasing the ∆P for the rejected bids by a constant
0.2 as described in equation (9) for the smooth bid-
ding agents or varying the bidding strategy in a range
from ∆P =0.1 to 1.5 (see Table 2) for the aggressive
bidding agents. Beginning with one bundle contain-
ing three XOR bids (m =3) in round one, both types
of agents generated three additional bids (o =3)in
each further round k. The bids were held and in-
creased by ∆P over a maximum of l =5rounds in
case of non-acceptance. The pattern of the new gener-
ated bids was identical to the structured BM type de-
scribed in Table 1 (q
bmax
=3,p
tso
=0.333,t
max
=
4). The auctioneer could allocate a maximum load of
q
max
=8per resource while T was ten time units
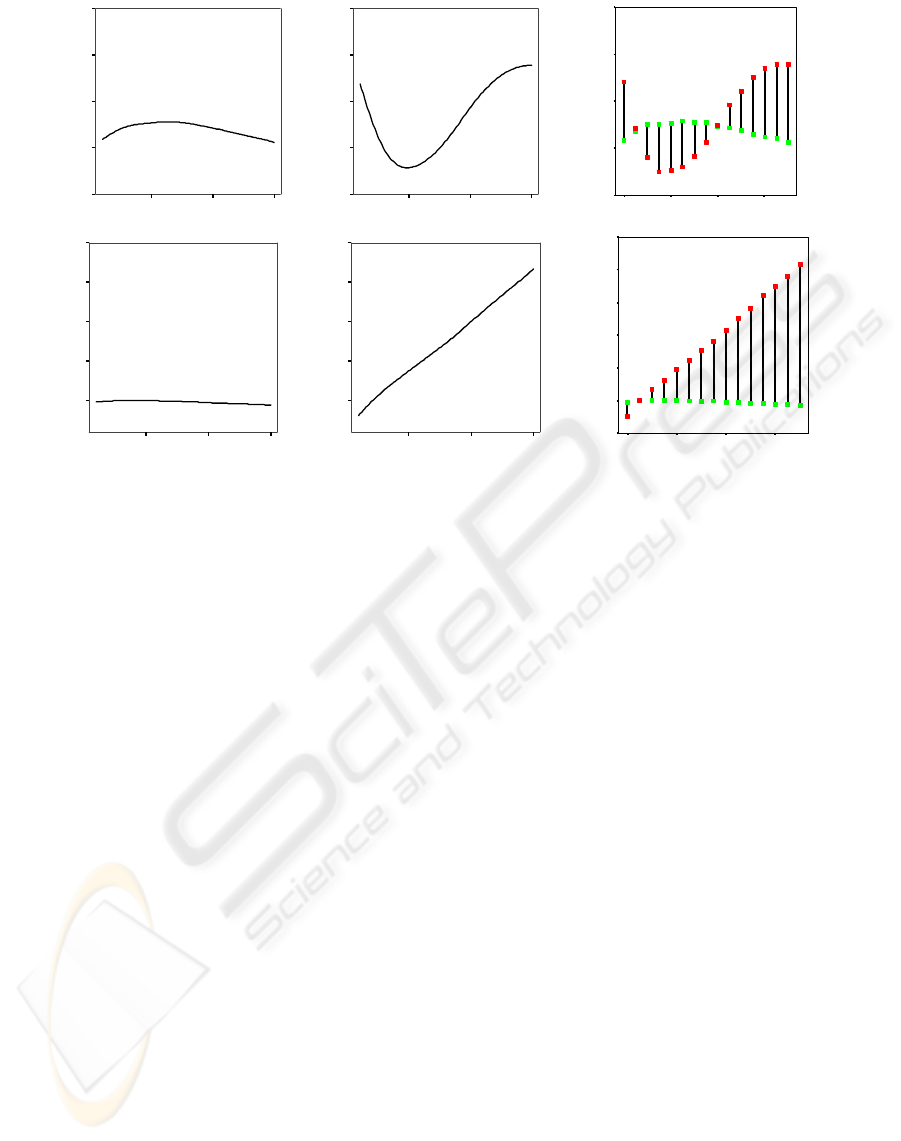
for the length of the AM . Figure 3 shows the results
of the strategy simulations, 100 runs for each ∆P in
0.1 steps. The aggressive bidder competes fiercely
against three smooth bidders. In the upper part of Fig-
ure 3, the mean round time until bid acceptance can be
seen, whereas the lower part depicts a mean of budget
spending per acquired resource unit. For an increas-
ing aggressive agent the mean acceptance time
¯
k
acc
aggr
is reduced by 0.25 for ∆P =0.4, 0.5 and 0.6 com-
pared to, the average acceptance time
¯
k
acc
smoo
of the
smooth bidder (See Table 2.). While rising ∆P , the
average acquisition price ∆¯p per resource unit (over
all resource types) increases linear for the aggressive
bidder (See Figure 3 lower part.). As illustrated in Ta-
ble 2, the optimal strategy for the aggressive bidder
is a price increment of ∆P =0.4 resulting in
¯
k
acc
aggr
reduced by ∆
¯
k
acc
=0.25 with an average resource
price increment of ∆¯p =0.12 if the agents’ utility is
defined by U
aggr
= −
¯
k
acc
− 0.1 · ∆¯p yielding 0.23.
U
aggr
is a trade-off between fast bid acceptance and
high resource costs in favor of short acceptance time.
5 CONCLUSION
We presented an agent-based simulation environment
for a grid scheduler that enables the simultaneous al-
location of resources in a grid-like computer system.
USING SHADOW PRICES FOR RESOURCE ALLOCATION IN A COMBINATORIAL GRID WITH
PROXY-BIDDING AGENTS
17

Table 2: Efficiency of two competing bidding strategies (smooth, aggressive) in terms of mean price per acquired resource
unit ¯p and average round time
¯
k
acc
until bid acceptance.
price increment ∆P
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5
¯p
smoo
0.99 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.99 0.99 0.98 0.98 0.98 0.98 0.97
¯p
aggr
0.90 1.00 1.07 1.13 1.19 1.25 1.31 1.36 1.43 1.51 1.57 1.64 1.70 1.76 1.83
¯
k
acc
smoo
1.30 1.34 1.38 1.38 1.38 1.40 1.39 1.39 1.37 1.36 1.35 1.33 1.31 1.30 1.28
¯
k
acc
aggr
1.60 1.36 1.20 1.13 1.13 1.15 1.21 1.28 1.37 1.48 1.56 1.63 1.67 1.69 1.69
∆¯p -0.09 0.0 0.07 0.12 0.19 0.25 0.31 0,36 0.43 0.52 0.58 0.66 0.72 0.79 0.86
∆
¯
k
acc
0.31 0.01 -0.18 -0.25 -0.25 -0.25 -0.18 -0.11 0.0 0.12 0.21 0.30 0.36 0.39 0.41
U
aggr
-0.29 -0.01 0.16 0.23 0.21 0.20 0.12 0.04 -0.09 -0.22 -0.33 -0.43 -0.51 -0.55 -0.59
Allocation is done by a combinatorial auction in our
economically inspired approach where proxy-agents
try to acquire optimal resource bundles with respect
to limited budgets. The system allows the provi-
sion of price information for the resources required
to perform various information services and informa-
tion production tasks in the grid. This is done by
calculating shadow prices in connection with solving
the NP-hard winner determination problem of the
combinatorial auction by an integer programming ap-
proach. The efficiency of the shadow price-based al-
location was tested in a closed loop grid system where
the agents can use monetary units rewarded for the
resources they provide to the system for the acqui-
sition of complementary capacity. Two types of bid-
ding agents have been compared in terms of efficiency
(average resource price payed and waiting time until
bid acceptance): An aggressive bidding agent with
strongly rising bids and a smooth bidding agent us-
ing low bid increments. While searching the strategy
space by varying the bidding behavior of the aggres-
sive agent from smooth to very aggressive in a com-
petitive environment with multiple smooth bidders, it
turns out that there is a bidding strategy where trade-
off between bid acceptance time and average resource
price paid is optimal. Future research will address
system behavior in resource failure situations and the
question of incentive compatible bidding. Addition-
ally, the question of alternative definitions of the util-
ity function for the different agent types should be dis-
cussed.
REFERENCES
AuYoung, A., Chun, B. N., Snoeren, A. C., and Vahdat,
A. (2004). Resource allocation in federated distrib-
uted computing infrastructures. In Proceedings of the
1st Workshop on Operating System and Architectural
Support, San Francisco, USA.
Bjørndal, M. and Jørnsten, K. (2001). An analysis of a com-
binatorial auction. Technical Report 2001-11, Depart-
ment of Finance and Management Science, Norwe-
gian School of Economics and Business Administra-
tion, Bergen, Norway.
Buyya, R., Stockinger, H., Giddy, J., and Abramson,
D. (2001). Economic models for management of
resources in peer-to-peer and grid computing. In
Proceedings of the SPIE International Conference
on Commercial Applications for High-Performance
Computing, Denver, USA.
Chun, B. N., Buonadonna, P., AuYoung, A., Ng, C., Parkes,
D. C., Shneiderman, J., Snoeren, A. C., and Vahdat, A.
(2004). Mirage: A microeconomic resource allocation
system for sensornet testbeds. In Proceedings of the
2nd IEEE Workshop on Embedded Networked Sensors
(EmNetS-II); Sidney, Australia.
Fujishima, Y., Leyton-Brown, K., and Shoham, Y. (1999).
Taming the computational complexity of combinato-
rial auctions: Optimal and approximate approaches.
In Proceedings of the 16th International Joint Confer-
ence on Artificial Intelligence 1999 (IJCAI-99), Stock-
holm, Sweden, pages 548 – 553.
Kwasnica, A. M., Ledyard, J., Porter, D., and DeMartini,
C. (2005). A new and improved design for multi-
objective iterative auctions. Management Science,
51(3):419–434.
Nisan, N. (2005). Bidding languages. In Steinberg, R.,
Shoham, Y., and Cramton, P., editors, Combinatorial
Auctions. MIT-Press.
Parkes, D. C. and Ungar, L. H. (2000). Iterative combina-
torial auctions: Theory and practice. In Proceedings
of the 17th National Conference on Artificial Intelli-
gence (AAAI-00), pages 74–81.
Rassenti, J. S., Smith, V. L., and Bulfin, R. L. (1982). A
combinatorial auction mechanism for airport time slot
allocation. Bell Journ. of Economics, 13(2):402–417.
Schwind, M., Stockheim, T., and Rothlauf, F. (2003). Op-
timization heuristics for the combinatorial auction
problem. In Proceedings of the Congress on Evolu-
tionary Computation CEC 2003, pages 1588–1595.
Vries, S. D. and Vohra, R. (2001). Combinatorial auc-
tions: A survey. INFORMS Journal on Computing,
15(3):284–309.
Xia, M., Koehler, G. J., and Whinston, A. B. (2004). Pricing
combinatorial auctions. European Journal of Opera-
tional Research, 154(1):251–270.
ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING
18
