
FILTERING UNSATISFIABLE XPATH QUERIES
Jinghua Groppe, Sven Groppe
Digital Enterprise Research Institute (DERI), University of Innsbruck, Institute of Computer Science, AT-6020 Innsbruck
Keywords: Queries, XML, XPath, satisfiability tester, query optimization.
Abstract: Empty results of queries are a hint for semantic errors in users’ queries, and erroneous and unoptimized
queries can lead to highly inefficient processing of queries. For manual optimization, which is prone to
errors, a user needs to be familiar with the schema of the queried data and with implementation details of
the used query engine. Thus, automatic optimization techniques have been developed and have been used
for decades in database management systems for the deductive and relational world. We focus on the
satisfiability problem for the queries formulated in the XML query language XPath. We propose a schema-
based approach to check whether or not an XPath query conforms to the constraints given in the schema in
order to detect semantic errors, and in order to avoid unnecessary evaluations of unsatisfiable queries.
1 INTRODUCTION
XPath (W3C, 1999) (W3C, 2003) is either a
standalone XML query language or is embedded in
other XML languages (e.g. XSLT, XQuery, XLink
and XPointer) for specifying node sets in XML
documents. Different from the query languages for
relational databases, XPath supports complex
navigational paths and qualifiers. Thus, it is not
trivial to develop efficient XPath evaluators and
many current implementations of XPath evaluators
have a high runtime complexity (Gottlob et al.,
2002). There has been work on physical
optimization of XPath expressions, i.e. efficient
algorithms for XPath evaluation, e.g. the XPath
evaluator proposed in (Gottlob et al., 2002), which
considers bottom-up processing of XPath
expressions, indexing techniques (Rao et al., 2004)
(Wang et al., 2003) and structural join algorithms
(Jiang et al., 2003) (Bruno et al., 2002). Many
research efforts focus on the minimization of XPath
expressions (Amer-Uahis et al., 2001) (Ramanan,
2002) since the size of XPath expressions
significantly impacts the processing of queries. The
study on the minimality of XPath actually relates to
the issues of the equivalence and containment with
respect to two XPath queries (Miklau et al., 2002)
(Wood, 2000). Currently, logical rewriting and
optimization of XPath expressions attract more
attention (Olteanu et al., 2002) (Benedikt et al. 2003)
(Chan et al., 2004). The satisfiability problem of
XPath queries is another important determinant of
XPath evaluation. An XPath query is satisfiable if
there exists a document on which the evaluation of
the XPath query returns a non-empty result.
Therefore, using the satisfiability test can avoid the
submission and unnecessary computation of an
unsatisfiable XPath query, and thus saves users’ cost
and evaluation time. One of our contributions is to
show how we can detect unsatisfiable queries based
on schema information.
Since schemas impose the constraints of the
structure and vocabulary of XML documents,
schemas provide an additional dimension for the
satisfiability check of XPath. Our approach supports
the recursive as well as non-recursive schemas and
all XPath axes. The most widely used schema
languages are XML Schema (W3C, 2004) and DTD
(W3C, 1998), but only DTDs are used in the existing
work. In this paper, we focus on XML Schema for
the definition of schemas. An XML Schema can
express more restrictions than a DTD. Thus, a DTD
can be easily transformed into an XML Schema
representation, but in general, an XML Schema
definition cannot be transformed into a DTD.
A common XPath evaluator is typically constructed
to evaluate XPath queries on XML documents. Our
approach modifies the common XPath evaluator in
order to evaluate XPath queries on XML Schema
definitions rather than the instance documents of the
schemas. Since the satisfiability test for the class of
XPath queries supported by our approach in the
presence of schemas is undecidable (Benedikt et al.,
2005), we present a fast, but incomplete satisfiability
tester, i.e. for the satisfiability test of XPath queries,
our approach computes to one of the following
157
Groppe J. and Groppe S. (2006).
FILTERING UNSATISFIABLE XPATH QUERIES.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 157-162
DOI: 10.5220/0002465001570162
Copyright
c
SciTePress

results: {unsatisfiable, maybe satisfiable}. Whereas
we are sure that the XPath query is unsatisfiable,
whenever our satisfiability tester returns
unsatisfiable, we cannot be sure that the XPath
query is satisfiable if our satisfiability tester returns
maybe satisfiable.
Related Work. Several contributions focus on
the satisfiability problem of XPath queries.
(Benedikt et al., 2005) theoretically studies the
complexity problem of XPath satisfiability in the
presence of DTDs, and shows that the complexity of
XPath satisfiability depends on the considered
subsets of XPath expressions and DTDs. We present
a practical algorithm for testing the satisfiability of
XPath queries. (Hidders, 2003) investigates the
problem of satisfiability of XPath expressions in the
absence of schemas. (Lakshmanan et al., 2004)
examines the test of satisfiability of tree pattern
queries (i.e. reverse axes are not considered) with
respect to non-recursive schemas. (Kwong et al.,
2002) suggests an algorithm to test the satisfiability
of XPath queries, but allows only non-recursive
DTDs and does not support all XPath axes. We
support recursive schemas and all XPath axes.
(Groppe et al., 2006) filters the unsatisfiable XPah
queries by a set of simplification rules while we use
the constraints given by an XML Schema definition
to check the satisfiability of XPath. (Groppe, 2005)
extends the applications of satisfiability testers to
optimizations for XML query reformulation and
shows how to reduce the containment and
intersection test of XPath expressions to the
satisfiability test.
The rest of the paper is organized as follows. Section
2 defines the XML Schema subset and XPath subset
supported by our approach. Section 3 develops a
data model of XML Schema for evaluating XPath
queries on an XML Schema definition. Section 4
presents our approach, the XSchema-XPath
evaluator, including the satisfiability test of XPath
expressions. This paper ends up with the summary
and conclusions in Section 5.
2 XML SCHEMA AND XPATH
Due to space limitations, we do not introduce XML
Schema here, but we refer readers to the
specification (W3C, 2004). We support the subset of
the XML Schema language, which contains the most
important language constructs to express XML
Schema definitions, where a given XML Schema
definition must conform to the following rules
defined in Extended Backus Naur Form (EBNF).
XSchema::= <schema> (elemD|attrGD|groupD|compTD)*
</schema>.
elemD::= <elem name='N' occurs? (type=’T’)?>
<compT (mixed='true')? (ref='N')?>
compT? </compT> (attrR|attrD)* </elem>.
groupD::= <group name='N'> compT? </group>.
compTD::= <compT name='N'> compT </compT>.
compT::= <all occurs?> compT? </all> | <seq occurs?>
compT? </seq> | (elems | groupR)*.
elems::= (elemD | <elem ref='N' occurs? />)*.
groupR::= <group ref='N'/>.
attrR::= <attrG ref='N'/>.
attrGD::= <attrG name='N'> (attrD)* </attrG>.
attrD::= <attr name='N' type=’T’ (use=’required’)?/>
occurs::= minO=num maxO=(num|'unbounded').
where T is a simple type, N is a name and num is a
number. Furthermore, we use
elem as short name for
element, compT for complexType, seq for sequence, attrG
for
attributeGroup, attr for attribute, minO for minOccurs and
maxO for maxOccurs.
Example 1: Figure 1 presents an example of an
XML Schema definition bib.xsd.
(D1) <schema> <group name='jArticle'> <seq>
(D2) <elem name='article' minO='1' maxO='1'>
(D3) <compT> <seq>
(D4) <elem name='year' minO='0' maxO='1’ type='string'/>
(D5) <elem name='ref' minO='0' maxO='1'>
(D6) <compT> <group ref='jArticle' minO='0'
maxO='unbounded'/> </compT> </elem>
</seq></compT></elem></seq></group>
(D7) <elem name='bib'>
(D8) <compT><group ref='jArticle' minO='0'
maxO='unbounded'/> </compT> </elem>
</schema>
Figure 1: An XML Schema definition bib.xsd.
In this paper, we consider the basic properties of the
XPath language. Due to space limitations, we do not
introduce XPath here, but we refer readers to the
specifications (W3C, 1999) and (W3C, 2003). Let e
be an XPath expression, q be a predicate expression
of XPath and C be a literal, i.e. a string or a number.
The abstract syntax of the supported XPath subset is
defined in EBNF as follows:
e::= e|e | /e | e/e | e[q] | axis::nodetest.
q::= e | e=C | e=e | q and q | q or q | not(q) | (q) | true() | false().
axis::= child | attr | desc | self | following | preceding | parent |
ances | DoS | AoS | FS | PS.
nodetest::= tagname | ∗ | node() | text().
where we write DoS for descendant-or-self, AoS for
ancestor-or-self, FS for following-sibling and PS for
preceding-sibling. Furthermore, we use attr as short
name for
attribute, desc for descendant and ances for
ancestor.
3 DATA MODEL FOR XML
SCHEMA
Based-on the data models for the XML language
given by (Wadler, 2000) and (Olteanu et al., 2002),
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
158

we develop a data model for XML Schema for
identifying the navigation paths of XPath queries on
an XML Schema definition. The transitive closure f
+
and reflexive transitive closure f* of a relationship
function f:T→Set(T) are defined as follows:
f
n
(x) = { z | y∈f
n-1
(x) ∧ z∈f(y) }, where f
0
(x) = {x}, f
1
(x) = f (x)
f
+
(x)
= ∪
n=1
∞
f
n
(x) and f *(x) = ∪
n=0
∞
f
n
(x)
An XML Schema definition is a set of nodes of type
Node.
There are four specific Node types in XML
Schema definitions, which are associated with
instance nodes of the schema:
root, iElem, iAttr and
iText.
Accordingly, we define four functions of
Node→Boolean to test the type of a node: isRoot, isiElem,
isiAttr, and isiText, which return true if the type of the
given node is a root node, is of type
iElem, iAttr or iText
respectively, otherwise false.
Definition 1 (instance nodes): The instance nodes
of an XML Schema definition are
• <elem name=N> (which is of type iElem),
• <attr name=N> (which is of type iAttr),
• <compT mixed= ‘true’>
(which is of type iText),
• <elem type=T> (which is of type iText), where T is
a
simpleT.
Definition 2 (succeeding nodes): A node N2 in an
XML Schema definition is a succeeding node of a
node
N1 in the XML Schema definition if
• N2 is a child node of N1, or
• N1=<elem type=N> and N2=<compT name=N> with
the same
N, or
• N1=<elem ref=N>
and N2=<elem name=N> with the
same
N, or
• N1=<group ref=N> and N2=<group name=N> with the
same
N, or
• N1=<attrG ref=N> and N2=<attrG name=N> with the
same
N.
Definition 3 (preceding nodes): Node N1 in an
XML Schema definition is a preceding node of a
node
N2 in the XML Schema definition if N2 is a
succeeding node of
N1.
Figure 2 defines the relation functions of
Node→Set(Node), which relate a schema node to other
schema nodes. For instances,
root(x) returns the root
node of the document in which
x occurs; iChild relates
a node to its instance child nodes. For computing
iChild(x), an auxiliary function S(x) is defined, which
relates the node
x to the self node and all the
descendant nodes of
x, which occur before the
instance child nodes of
x in the document order. iDesc
relates a node to all its instance descendant nodes
and is defined to be the transitive closure
iChild
+
. The
relation function
iSibling(x) relates the node x to its
instance sibling nodes.
iBranch(x) relates node x to all
the instance element nodes excluding any ancestors
and descendants of the node
x. iPS(x) relates the node
x to its instance sibling nodes that occur before node
x in the document order, and iPreceding(x) relates node
x to its instance branch nodes that occur before node
x in the document order. We write y<<x to indicate
that the node
y occurs before the node x in the
document order of an instance document. The
document order is computed from an XML Schema
definition in the following way: if a set of elements
is declared as
seq with the attribute maxO set to 1, the
document order of elements is the order in which
they are defined; if it is declared as
all or as seq with
the attribute
maxO set to a number greater than 1, any
element of this set of elements can occur before any
other elements of this element set in an instance
document.
root(x) = { y | isRoot(y)}
succeeding(x) = { y | y is a succeeding node of x }
preceding(x) = { y | y is preceding node of x }
S(x) = ∪
i=0
∞
S
i
, where S
0
= {x}, S
i
= { z | y∈S
i-1
∧
z∈succeeding(y) ∧ ¬isiElem(z) ∧ ¬isiAttr(z) }
P(x) = ∪
i=0
∞
P
i
, where P
0
= {x}, P
i
= { z | y∈P
i-1
∧
z∈preceding(y) ∧ ¬isiElem(z) ∧ ¬isiAttri(z) }
iChild(x) = { z | y∈S(x) ∧ z∈succeeding(y) ∧
( isiElem(z) ∨ isiText(z) ) }
iAttribute(x) = { z | y∈S(x) ∧ z∈succeeding(y) ∧ isiAttr(z) }
iParent(x) = { z | y∈P(x) ∧ z∈preceding(y) ∧ isiElem(z) }
iDesc(x) = {z | z∈iChild
+
(x)}
iAnces(x) = {z | z∈iParent
+
(x)}
iDoS(x) = {z | z∈iChild
∗
(x)}
iAoS(x) = {z | z∈iParent
∗
(x)}
iSibling(x) = {y | z∈iParent(x) ∧ y∈iChild(z)}
iBranch(x) = {y | y∈iChild
+
(root(x)) ∧ y ∉iParent
∗
(x) ∧
y ∉iChild
+
(x) ∧ ¬isiAttr(y)}
iPS(x) = {y | y∈iSibling(x) ∧ y << x}
iFS(x) = {y | y∈iSibling(x) ∧ x << y}
iPreceding(x) = {y | y∈iBranch(x) ∧ y << x }
iFollowing(x) = {y | y∈iBranch(x) ∧ x << y}
Figure 2: Used relation functions.
Let nodeTest be the type of the node tests of XPath.
An auxiliary function
attr(x, name) retrieves the value
of the attribute
name of the node x. The function NT,
which tests a schema node against a node test of
XPath, is defined as:
NT: Node × NodeTest → Boolean
• NT(x, tagname) = ( isiElem(x) ∧ (attr(x, name)=tagname)
)
∨ ( isiAttr(x) ∧ (attr(x, name)=tagname) )
• NT(x, ∗) = isiElem(x) ∨ isiAttr(x)
• NT(x, node()) = true
• NT(x, text()) = isiText(x)
4 XSCHEMA-XPATH
EVALUATOR
As a variant of a common XPath evaluator, our
XSchema-XPath evaluator evaluates XPath
expressions on an XML Schema definition rather
than XML instance documents. Instead of
FILTERING UNSATISFIABLE XPATH QUERIES
159

computing the node set of a given instance XML
document, our XSchema-XPath evaluator computes
a set of schema paths to the possible nodes specified
by a given XPath query when the XPath query is
evaluated by a common XPath evaluator on XML
instance documents. If an XPath query cannot be
evaluated completely, the schema paths for the
XPath query are computed to an empty set of
schema paths, i.e. the XPath query is unsatisfiable
according to the schema.
Definition 4 (Schema paths): A schema path is a
sequence of pointers to either the records <XP’, N, z, lp,
f>
or the records <o, {f, …, f}>, where
• XP’ is an XPath expression,
• N is a node in an XML Schema definition,
• z is a set of pointers
• lp
is a set of schema paths,
• f is a schema path list, or a predicate
expression without location steps, and
• o is a keyword.
XP’ is the part of a given XPath expression, which
has been evaluated;
N is a resultant node of a schema
whenever XP’ is evaluated by our XSchema-XPath
evaluator on the schema definition; z is a set of
pointers to the records in which the schema node is
the parent of the schema node of the current record.
Note whenever a record is the first record of a loop,
the record has more than one possible parent record.
lp represents loop schema paths; f represents either a
schema path list computed from a predicate
q that
test the node N, or the predicate expression q itself
from which no schema paths can be computed like
true() or false(), but also including self::node()=C. o
represents operators like or, and and not.
4.1 Computing Schema Paths
We use the technique of the denotational semantics
(Schmidt, 1994) to describe our XSchema-XPath
evaluator, and define the following notations. Let
z
be a pointer in a schema path and
d is a field of a
schema record, we write
z.d to refer to the field d of
the record to which the pointer
z points. We use the
letter S to represent the size of a schema path p, thus
p(S) to represent the last pointer, p(S-1) the pre-last
pointer, and so on.
Figure 3 defines the denotational semantic
L of the
XSchema-XPath evaluator. The function
L takes an
XPath expression and a schema path as the
arguments and yields a set of new schema paths, and
is defined recursively on the structure of XPath
expressions. For evaluating each location step of an
XPath expression, our XSchema-XPath evaluator
first computes the axis and the node test of the
location step by iteratively taking the schema node
p(S).N from each schema path p in the path set as the
context node. The path set is computed from the part
xp’’ of the XPath query, which has been evaluated by
the XSchema-XPath evaluator. For each resultant
node r selected by the current location step
xp
f
, a new
schema path is generated based on the old path
p.
The auxiliary function ϑ(r, g) generates a new schema
path record e=<xp’, r, g, -, ->, adds a pointer to e at the
end of the given schema path
p and returns a new
schema path, where xp’=xp’’/xp
f
and g is a set of
pointers.
In the case of recursive schemas, it may occur
that the XSchema-XPath evaluator revisits a node
N
of the XML Schema definition without any progress
in the processing of the query. We call this a loop. A
loop might occur when an XPath query contains the
axis
desc, ances, preceding or following, which are boiled
down to the recursive evaluation of the axis child or
parent respectively. We detect loops in the following
way: let
r be a visited schema node when evaluating
the part
xp’ of an XPath expression with p(S).N as the
context node. If there exists a record
p(i) in p, such
that
p(i).N=r, and p(i).XP’=xp’, a loop is detected and the
loop path segment is
lp = (p(i), …,p(S)). lp will be
attached to the schema node
p(i).N where the loop
occurs. For computing
L⎡desc::n⎦(p), we first compute
p
i
| p
i
∈L⎡child::*⎦(p
i-1
) where p
1
=L⎡child::*⎦(p). If no loop is
detected in the path p
i
, i.e. ∀i∈{1, ..., S-1}: p
i
(i).N≠p
i
(S).N
∧ p
i
(i).XP’≠p
i
(S).XP’, L’⎡self::n⎦(p
i
) is then computed in
order to construct a possible new path from
p
i
. If a
loop is detected in the path
p
i
, i.e. ∃k∈{1,.., S-1}:
p
i
(k).N=p
i
(S).N ∧ p
i
(k).XP’=p
i
(S).XP’, a loop path segment,
i.e.
{p
i
(k), …, p
i
(S-1)} is identified. The function X
modifies the record, which is the head of the loop,
by adding the loop path into the record, i.e.
X(p
i
(k),
(p
i
(k),..,p(S-1))), and returns true. Furthermore,
although the schema nodes in two records are the
same, i.e.
p
i
(k).N=p
i
(S).N, these two nodes have
different parents, i.e,
p
i
(k).z ≠ p
i
(S).z. Therefore, the
new parent
p
i
(S).z has to be recorded and this is done
by the function
Z, which adds a parent pointer to the
record
p
i
(k), i.e. Z(p
i
(k), p
i
(S).z), and returns true.
The schema paths of a predicate are attached to
the context node of the predicate. The function
A(F, i,
p) writes F into the field p(i).f and returns the modified
schema path
p. The parameter F = {f
1
,..,f
k
} is computed
from a set of predicates
q
1
,..q
k
. f
i
is either a schema
path list computed from a predicate
q
i
, or is the
predicate expression
q
i
itself when q
i
does not contain
location steps. The node
p(i).N is the context node of
these predicates.
q
i
is evaluated to false if q
i
is
computed to the empty schema paths with the
exception of
not(q), which is computed to true. For
instance,
L⎡e[q
1
and q
2
]⎦(p) is computed to empty paths
if
q
1
or q
2
are evaluated to false. When computing the
schema paths of a predicate, the XSchema-XPath
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
160
evaluator initializes a schema path variable
f with
null, which is logically concatenated with the main
path
p, denoted by p+f, for the need of both finding
the context node of the predicate and finding the
nodes specified by reverse axes in the predicate,
which occur before the context node of the predicate
in the document order.
L: XPath expression × schem path → set(schem path)
• L⎡e1|e2⎦(p) = L⎡e1⎦(p) ∪ L⎡e2⎦(p)
• L⎡/e⎦(p) = L⎡e⎦(p
1
) ∧ p
1
=( </,/,-, -, - > )
• L⎡e1/e2⎦(p) = { p
2
| p
2
∈L⎡e2⎦(p
1
)
∧ p
1
∈L⎡e1⎦(p) }
• L⎡self::n⎦(p) = { ϑ(p(S).N, p(S).z) | NT(p(S).N, n) }
• L⎡child::n⎦(p) = {ϑ(r, p(S)) | r∈iChild(p(S).N) ∧ NT(r,n) }
• L⎡attr::n⎦(p) = { ϑ(r, p(S)) | r∈iAttr(p(S).N) ∧ NT(r,n) }
• L’⎡self::n⎦(p) = { p | NT(p(S).N, n) }
• L⎡desc::n⎦(p) = { p’ | p’∈∪
i=1
∞
L’⎡self::n⎦(p
i
) ∧
∀k∈{1, …, S-1 }: p
i
(k).N≠p
i
(S).N ∧ p
i
(k).XP’≠p
i
(S).XP’
where p
i
∈L⎡child::∗⎦(p
i-1
)
∧ p
1
∈L⎡child::∗⎦(p), or
p’∈∪
i=1
∞
L’⎡self::n⎦(p
i-1
)
∧ X(p
i
(k), (p
i
(k),..,p(S-1))) ∧
Z(p
i
(k), p
i
(S).z)) ∧ ∃k∈{ 1,.., S-1 }:
p
i
(k).N=p
i
(S).N ∧ p
i
(k).XP’=p
i
(S).XP’,
where p
i
∈L⎡child::∗⎦(p
i-1
)
∧ p
i-1
∈ L⎡child::*⎦(p
i-2
) ∧
p
1
∈L⎡child::∗⎦(p).
• L⎡DoS::n⎦(p)= L⎡self::n⎦(p) ∪ L⎡desc::n⎦(p)
• L⎡parent::n⎦(p) = { ϑ(r, x)| r=Z1.N ∧ Z1∈p(S).z ∧ x=Z1.z ∧
NT(r,n) }
• L⎡ances::n⎦(p) = { p’ | p’∈∪
i=1
∞
L’⎡self::n⎦(p
i
) ∧
∀k∈{1,.., S-1}: p
i
(k).N≠p
i
(S).N ∧ p
i
(k).XP’≠p
i
(S).XP’,
where p
i
∈L⎡parent::∗⎦(p
i-1
) ∧ p
1
∈L⎡parent::∗⎦(p)
,
or
p’∈∪
i=1
∞
L’⎡self::n⎦(p
i-1
)
∧ X(p
i
(k), (p
i
(k),..,p(S-1))) ∧
Z(p
i
(k), p
i
(S).z)) ∧ ∃k∈{1,.., S-1}:
p
i
(k).N=p
i
(S).N ∧ p
i
(k).XP’=p
i
(S).XP’,
where p
i
∈L⎡parent::∗⎦(p
i-1
) ∧ p
i-1
∈L⎡parent::*⎦(p
i-2
) ∧
p
1
∈L⎡parent::∗⎦(p).
• L⎡AoS::n⎦(p) = L⎡self::n⎦(p) ∪ L⎡ances::n⎦(p)
• L⎡FS::n⎦(p) = { ϑ(r, p(S).z) | r∈iFS(p(S).N) ∧ NT(r,n) }
• L⎡following::n⎦(p) = L⎡AoS:: ∗/FS :: ∗/DoS::n⎦(p)
• L⎡PS::n⎦(p) = { ϑ(r, p(S).z) | r∈iPS(p(S).N) ∧ NT(r,n) }
• L⎡preceding::n⎦(p) = L⎡AoS:: ∗/PS :: ∗/DoS ::n⎦(p)
• L⎡e[q]⎦(p) = A( {L⎡q⎦(p’+f)}, S, p’ ), where f=∅ ∧ p’∈L⎡e⎦(p)
• L⎡e[q
1
[q
2
]]⎦(p) = A( {L⎡q
1
[q
2
]⎦(p’+f)}, S, p’ ),
where f=∅ ∧ p’∈L⎡e⎦(p)
• L⎡e[self::node()=C]⎦(p) = A( {‘self::node()=C’}, S, p’ ),
where p’∈L⎡e⎦(p)
• L⎡e[q = C]⎦(p) = L⎡e[q[self::node()=C]]⎦(p)
• L⎡e[q
1
][q
2
]⎦(p) = A( {A( {L⎡q
2
⎦(p’+f
2
), L⎡q
1
⎦(p’+f
1
)}, S, f)}, S, p’),
where p’∈L⎡e⎦ (p) ∧ f=(<‘and’, ->) ∧ f
1
=∅ ∧ f
2
=∅.
• L⎡e[q
1
and q
2
]⎦(p) = L⎡e[q
1
][q
2
]⎦(p)
• L⎡e[q
1
or q
2
]⎦(p) = A( {A ({L⎡q
2
⎦(p’+f
2
), L⎡q
1
⎦(p’+f
1
)}, S, f)}, S, p’),
where p’∈L⎡e⎦(p) ∧ f=(<‘or’, ->) ∧ f
1
=∅ ∧ f
2
=∅.
• L⎡e[q
1
= q
2
]⎦(p) = A( {A ({L⎡q
2
⎦(p’+f
2
), L⎡q
1
⎦(p’+f
1
)}, S, f)}, S, p’),
where p’∈L⎡e⎦(p) ∧ f=(<‘=’, ->) ∧ f
1
=∅ ∧ f
2
=∅.
• L⎡e[not(q)]⎦(p) = A( {L⎡q
1
⎦(p’+f
1
)}, S, f) , where
f=(<‘not’, ->) ∧ p’∈L⎡e⎦ (p) ∧ f
1
=∅.
Figure 3: Formulas for constructing the schema paths.
Example 2: Our XSchema-XPath evaluator
evaluates an XPath query
Q in Figure 4 on the XML
Schema definition of Figure 1 and computes a
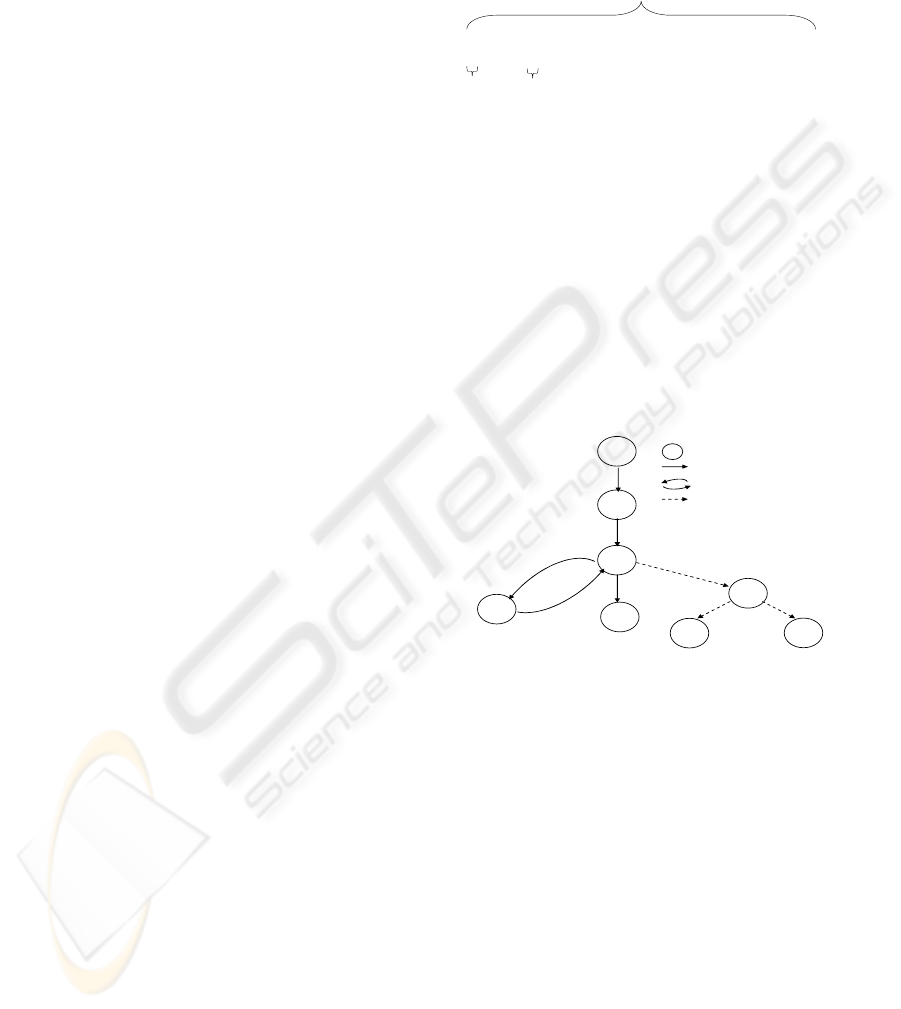
schema path (cf. Figure 5). Figure 6 is the graphical
representation of Figure 5, in which we only present
the schema node item of records of the schema path.
Figure 4: XPath query Q and its subexpressions.
(R1) { (</, /, -, -, -> ,
(R2) <S1, D7, {R1}, -, ->,
(R3) <S2, D2, {R2, R4},
(R4) {(<S2, D5, {R3}, -, ->)},
(R5) (<‘and’,
(R6) {(<S3, D4, {R3}, -, ->),
(R7) ‘true()’} > ) >,
(R8) <Q, D5, {R3}, -, -> )}
Figure 5: Schema paths of the query Q.
Figure 6: Graphical representation of the schema paths of
Figure 5.
4.2 Satisfiability Test
Definition 5 (Satisfiability of XPath querys): A
given XPath query
Q is satisfiable according to a
given XML Schema definition
XSD, if there exists an
XML document
D, which is valid according to XSD,
and the evaluation of
Q on D returns a non-empty
result. Otherwise
Q is unsatisfiable according to XSD.
Proposition 1 (Unsatisfiable XPath querys): A
given XPath query
Q is unsatisfiable according to a
given XML Schema definition
XSD if the evaluation
of
Q by the XSchema-XPath evaluator on XSD
generates an empty set of schema paths.
Proof. The XSchema-XPath evaluator is constructed
in such a way that the XSchema-XPath evaluator
returns an empty set of schema paths, if the
constraints given in
Q and the constraints given in
/bib//article[year][not(self::node()[editor]/AoS::node()[self::node()=‘bib’])]/parent::ref
S1
S2
S3
D7
/
D2
D5
‘and’
‘true()’
D4
D5
main schema path
loop schema path
predicate schema path
schema record
FILTERING UNSATISFIABLE XPATH QUERIES
161

XSD exclude the constraints of the other. Thus, there
does not exist a valid XML document according to
XSD, where the application of Q returns a non-empty
result.
If the XSchema-XPath evaluator computes a
non-empty set of schema paths for a given XPath
query
Q, the XPath query is only maybe satisfiable,
since the satisfiability test of XPath expressions
formulated in the supported subset of XPath is
undecidable (Benedikt et al., 2005).
5 SUMMARY AND
CONCLUSIONS
We have proposed a fast satisfiability tester of
XPath queries, the XSchema-XPath evaluator, which
evaluates XPath queries on recursive and non-
recursive XML Schema definitions. We have
developed a data model of the XML Schema
language to identify the node relationships parent-
child and next-sibling of declared XML nodes in
XML Schema definitions so that we can support all
XPath axes. Based on the data model, the
XSchema-XPath evaluator evaluates given XPath
queries on an XML Schema definition and generates
a set of schema paths. Whenever the set of schema
paths is computed to an empty set, the XPath query
is unsatisfiable, otherwise the XPath query is maybe
satisfiable.
The experimental results of our prototype (which we
do not present here due to space limitations) show
that our approach can significantly optimize the
evaluation of XPath queries by filtering unsatisfiable
XPath queries. A speed-up factor up to several
magnitudes is possible.
We will investigate how to support a bigger subset
of XPath in our future work.
ACKNOWLEDGEMENTS
This material is based upon works supported by the
EU funding under the Adaptive Services Grid
project (FP6 – 004617). Furthermore, this material is
based upon works supported by the Science
Foundation Ireland under Grant No.
SFI/02/CE1/I131.
REFERENCES
S. Amer-Uahis, S. Cho, L.K.S. Laksmanan, D. Srivastava,
2001. Mininization of tree pattern queries. In
SIGMOD’01.
M. Benedikt, W. Fan and G. M. Kuper, 2003. Structural
properties of XPath fragments. In ICDT’03.
M. Benedikt, W. Fan and F. Geerts, 2005. XPath
Satisfiability in the presence of DTDs. In PODS’03.
N. Bruno, N. Koudas, and D. Srivastava, 2002. Holistic
twig joins: optimal XML pattern matching. In
SIGMOD’02.
C.Y. Chan, W. Fan, and Y. Zeng, 2004. Taming XPath
Queries by Minimizing Wildcard Steps. In VLDB’04.
G. Gottlob, C. Koch, and R. Pichler, 2002. Efficient
Algorithms for Processing XPath Queries. In
VLDB’02.
S. Groppe, 2005. XML Query Reformulation for XPath,
XSLT and XQuery. Sierke-Verlag, Göttingen,
Germany. ISBN 3-933893-24-0.
S. Groppe, S. Böttcher and J. Groppe, 2006. XPath Query
Simplification with regard to the Elimination of
Intersect and Except Operators. In XSDM’06 in
conjunction with ICDE’06.
J. Hidders, 2003. Satisfiability of XPath Expressions,
DBPL’03, LNCS 2921, pp. 21 – 36.
H. Jiang, W. Wang, H. Lu and J. X. Yu, 2003. Holistic
twig joins on indexed XML documents. In VLDB’03.
L. Lakshmanan, G. Ramesh, H. Wang and X. Zhao, 2004.
On Testing Satisfiability of Tree Pattern Queries. In
VLDB’04.
A. Kwong and M. Gertz, 2002. Schema-based
optimization of XPath expressions. Techn. Report
University of California, California, USA.
G. Miklau and D. Suciu, 2002. Containment and
equivalence for an XPath fragment. In PODS’02.
D. Olteanu, H. Meuss, T. Furche, and F. Bry, 2002.
XPath: Looking Forward, XML-Based Data
Management (XMLDM), EDBT Workshops.
P. Ramanan, 2002. Efficient algorithms for minimizing
tree pattern queries. In SIGMOD’02.
P. Rao and B. Moon, 2004. PRIX: indexing and querying
XML using Prufer sequences. In ICDE’04.
D.A. Schmidt, 1994. The structure of Typed programming
languages. MIT Press, Cambridge, MA, USA.
P. Wadler, 2000. Two semantics for XPath. Tech. Report.
H. Wang, S. Park, W. Fan and P.S. Yu, 2003. ViST: a
dynamic index method for querying XML data by tree
structures. In SIGMOD’03.
P. T. Wood, 2000. On the equivalence of XML patterns.
In LNCS 1861, pages 1152-1166. Springer.
W3C, 1999. XML Path Language (XPath) Version 1.0,
W3C Recommendation, www.w3.org/TR/xpath/.
W3C, 2003. XML Path Language (XPath) Version 2.0,
W3C Working Draft, www.w3.org/TR/xpath20/.
W3C, 1998. Extensible Markup Language (XML) 1.0.
W3C Recommendation, www.w3.org/TR/REC-xml.
W3C, 2004. XML Schema Part 1: Structures Second
Edition. W3C Recommendation,
www.w3.org/TR/xmlschema-1.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
162
