
AUTOMATIC FEEDBACK GENERATION
Using Ontology in an Intelligent Tutoring System for both Learner
and Author Based on Student Model
Pooya Bakhtyari
Department of Computer Science, Tehran Polytechnic University, Hafez Ave., Tehran, Iran
Keywords: Intelligent Tutoring System, feedback, ontology, Student Model.
Abstract: Presenting feedback to learner is one of the essential elements needed for effective learning. Feedback can
be given to learners during learning but also to authors during course development. But producing valuable
feedback is often time consuming and makes delays. So with this reason and the others like incomplete and
inaccurate feedback generating by human, we think that it’s important to generate feedback automatically
for both learner and author in an intelligent tutoring system (ITS). In this research we used ontology to
create a rich supply of feedback. We designed all components of the ITS like course materials and learner
model based on ontology to share common understanding of the structure of information among other
software agents and make it easier to analyze the domain knowledge. With ontologies in fact, we specify the
knowledge to be learned and how the knowledge should be learned. In this paper we also show a
mechanism to make reason from the resources and learner model that it made feedbacks based on learner.
1 INTRODUCTION
No Learning would occur unless some type of
feedback mechanism was at work. Feedback can
increases motivation for learning and lets learners to
know the accuracy of their response to an
instructional question. It can compare the response
to some performance standard or provide further
guidance. Feedback provides information on
correctness, precision, comparisons, motivational
aspects, visual presentation, and guidance on
sequence of lessons. During the specification and
development of course material, many mistakes and
errors can be made. With these features, feedback
could also be helpful for author who presents the
lessons and correct his bugs in designing and
structuring the courses.
Emerging technologies have created new
possibilities for designing instructional feedback.
However, effective feedback depends on
pedagogical and psychological considerations.
Students need appropriate feedback on
performance to benefit from courses. When getting
started, students need help in assessing existing
knowledge and competence and need frequent
opportunities to perform and receive suggestions for
improvement. They also need chances to reflect on
what they have learned, what they still need to
know, and how to assess themselves.
In a classroom learners and teachers can easily
interact, i.e. students can freely ask questions and
teachers usually know whether their students
understand (basic) concepts or problem solving
techniques. Feedback is an important component of
this interaction. But there is a frequent lack of
feedback in electronic learning environment (or
eLearning) courses in higher education (Murray,
1999).
In our research, we want to develop generic,
domain and task independent feedback mechanisms
that produce semantically rich feedback to learners
and authors during learning and authoring. We will
develop generic feedback mechanisms where
ontologies are arguments of the feedback engine.
This is important, because the development of
feedback mechanisms is time consuming and
specialist work, and can be reused for different
ontologies. Besides generic feedback mechanisms
we will also develop mechanisms by means of
which authors can define domain and/or task
specific feedback.
This article is structured as follows: In Section 2,
we will compare our approach with related work. In
116
Bakhtyari P. (2006).
AUTOMATIC FEEDBACK GENERATION - Using Ontology in an Intelligent Tutoring System for both Learner and Author Based on Student Model.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - HCI, pages 116-123
DOI: 10.5220/0002466901160123
Copyright
c
SciTePress

Section 3, explains the designed student model and
the features that we considered in it for better
feedback generation. Section 4,5, presents the idea
for feedback generation to learner and author.
Section 6, introduces schema analysis and the
reasoning rules.
2 RELATED WORK
Although many authors underline the necessity of
feedback in authoring systems (Aroyo and Dicheva,
2004a; Aroyo and Mizoguchi, 2004c; Murray,
1999), we have found little literature about feedback
and feedback generation in authoring systems. Jin et
al. (Jin and Chen, 1999) describe an authoring
system that uses a domain as well as task ontology
to produce feedback to an author. The ontologies are
enriched with axioms, and on the basis of the axioms
the models developed can be verified and messages
of various kinds can be generated when authors
violate certain specified constraints. The details of
the techniques used are not given, and it is not clear
to us how general the techniques are. Our
contribution is the introduction of schema analysis
as a general technique to produce messages about
errors of structural aspects of course material.
Aroyo et al. (Aroyo and Dicheva (2004a, 2004b);
Aroyo and Mizoguchi, 2004c) describe a common
ontology (web) based authoring framework. The
framework contains a domain as well as task
ontology and supports an authoring process in terms
of goals, and primitive and composite tasks. Based
on ontologies, the framework monitors and assesses
the authoring process, and prevents and solves
inconsistencies and conflicting situations. Their
requirements for authoring support are: (1) help in
consistently building courseware, (2) discovery of
inconsistencies and conflicting situations, (3)
modularization of authoring systems (reusability),
(4) production of feedback, hints and
recommendations, and (5) allow accepting or
rejecting the proposed solutions. We think that our
framework satisfies all these requirements. Schema
analysis as a technique could be positioned in (1),
(2) and (4).
Stojanovic et al. (Stojanovic and Staab and
Studer, 2001) present an approach for implementing
eLearning scenarios using the semantic web
technologies XML and RDF, and make use of
ontology based descriptions of content, context and
structure. A high risk is observed that two authors
express the same topic in different ways
(homonyms). This problem is solved by integrating
a domain lexicon in the ontology and defining
mappings, expressed by the author itself, from terms
of the domain vocabulary to their meaning defined
by the ontology. In our approach these mappings are
analyzed automatically.
In the Authoring Adaptive Hypermedia
community the importance of feedback mechanisms
in authoring systems has been recognized (Cristea,
2004). Although we have found an impressive
amount of authoring tools for adaptive hypermedia
(Brusilovsky, 2003), we have not found descriptions
of technologies used for providing feedback to
authors. We expect our results will be useful for
authoring adaptive hypermedia as well.
3 STUDENT MODEL AND ITS
FEATURES
Student Model is an ITS component which keeps
track of specific information related to each
individual student, such as his mastery or
competence of the material being taught, and his
misconceptions. In effect, it stores the computer
tutor’s beliefs about the student. This information is
used by the pedagogical module to tailor its teaching
to the individual needs of the student.
Based on the subject of the domain, the
information stored in student models could be
divided into two major groups: domain specific
information and domain independent information.
The model of domain-specific information which is
named Student Knowledge Model (SKM)
(Brusilovsky, 1994), represents a reflection of the
student's state and his skills. Some of this
information could be:
• Student’s prior knowledge about the domain
• Records of learning behavior (number of
lectures taken, number of helps asked, frequency of
mistakes made while solving problems,
reaction/answering time while solving problems)
• Records of evaluation /assessment (qualitative
and quantitative scores).
A student model also needs to cover a certain
amount of domain-independent information in
addition to the student’s current knowledge level.
The domain-independent information about a
student may include learning goals, cognitive
aptitudes, measures for motivation state, preference
about the presentation method, factual and historic
data, etc.
AUTOMATIC FEEDBACK GENERATION - Using Ontology in an Intelligent Tutoring System for both Learner and
Author Based on Student Model
117
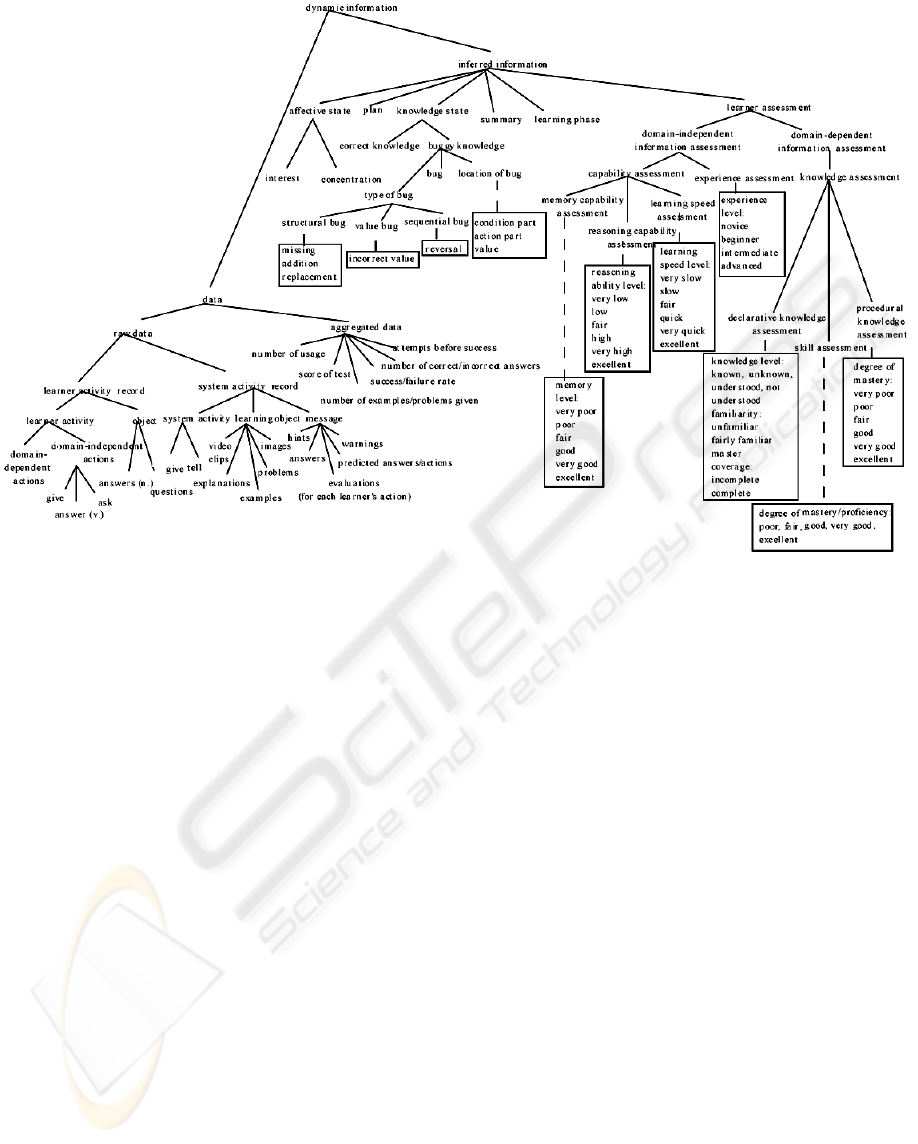
Figure 1: Part of Ontology based Student Model.
Our stress for better feedback generation is on
both cognitive aptitudes and learning styles
information and we think that these two information
type could help us respect to the others.
Shute (Shute, 1995) identified a number of
specific cognitive aptitudes besides student's general
attributes:
• General knowledge (GK)
• Inductive reasoning skill (IR)
• Working memory capacity (WM)
• Procedural learning skill (PL)
• Information processing speed (IPS)
• Associative learning skill (AL)
• Reflectivity
• Risk-taking.
The most important part of student preferences is
the learning style that is correlated with multiple
intelligence. Howard Gardner’s most current
research (Lane, 1998) defines eight distinct
intelligence forms stated as follows:
Verbal/linguistic intelligence
Logical/mathematical intelligence
Visual/spatial intelligence
Musical/rhythmic intelligence
Bodily/kin aesthetic intelligence
Intra-personal intelligence
Interpersonal intelligence
Naturalist intelligence
Gardner suggested that everyone possesses all
above form of intelligence but in varying capacity,
consequently one can show low ability in a domain
area but high ability in another domain. According
to the multiple intelligence theory, intelligent
educational system should be individualized so that
every student can be guided to achieve his or her
maximum potential (Lane, 2000).
With these two factors and the features that we
mention above, we introduce a student model based
on ontology (Figure 1) which included all of these
features.
In this designed ITS we have both student model
in individual and group form. The group student
model in many cases corrects the individual model
and also helps the author for presenting courses and
the contents based on each student and verifies them
better. This group student model is needed for both
student and author feedback generation and we
could produce feedbacks more accurately. Some
features from the student model that we consider as
aspects of the feedback generation, listed here:
• Student's Study Goal
• Cognitive Aptitudes
• Student Non-Domain Related Experiences
• Student Preferences
• Student Learning Style
• Student Study Time for Content Sections
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
118
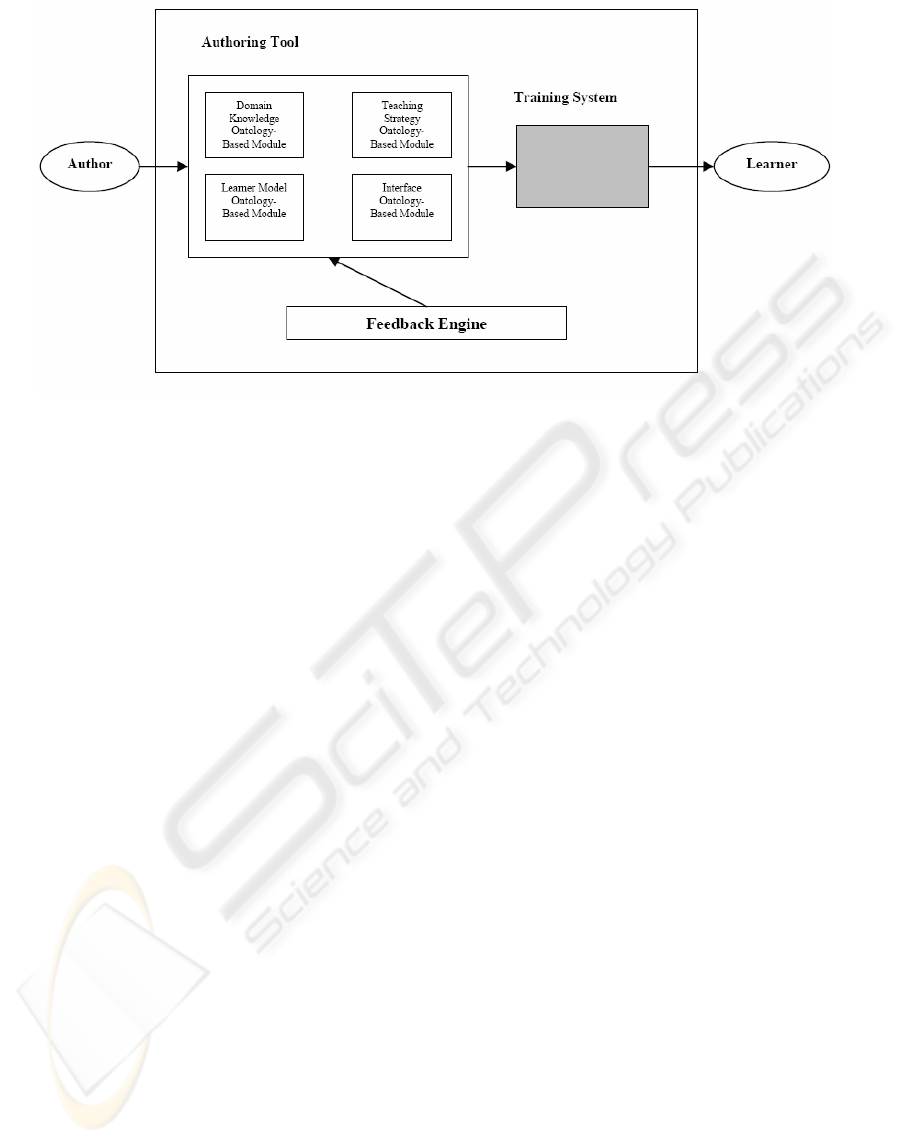
Figure 2: An ITS structure supported feedback generation module.
4 FEEDBACK GENERATION TO
LEARNER
To produce semantically rich feedback the system
should contain several types of knowledge and in
order to represent this knowledge we make use of
ontologies. At this moment, we distinguish
knowledge about:
• Domain – presents the contents of the ITS.
(Domain Knowledge Module)
• Student Model – presents the diagnosis of
system from student. (Learner Model Module)
• Education – For example: concept learning,
problem solving, examples and definitions.
(Teaching Strategy module)
• Feedback – presents the different types of
feedback and patterns/phases during dialogs.
Figure 2 gives the architecture of an ITS that
supports a generic feedback mechanism.
The Intelligent Tutoring environment consists of
three main components: a training system for the
learner, an authoring tool, a feedback engine, and
takes a set of ontologies as argument. The Training
System consists of a design and learning
environment in which a learner can learn concepts
and solve problems.
The authoring tool consists of an authoring
environment where the author develops and
maintains courses and course related materials like
ontologies, examples and feedback patterns. The
feedback engine automatically produces feedback to
learners as well as to authors. The learner receives
different types of feedback, for example
corrective/preventive feedback, critics and guiding
customized to the learning style of the learner.
The feedback engine produces generic feedback
and specific feedback. Generic feedback is
independent of the ontologies used. Specific
feedback is defined by the author and can be course,
domain or student knowledge specific. To construct
feedback, the feedback engine uses the four
argument ontologies. Since the ontologies are
arguments, the feedback engine doesn’t have to be
changed if the ontology is changed for another.
The feedback engine can produce the three above
mentioned types of feedback. To produce student
and author feedback, student and author activities
are observed and matched against the ontologies
mentioned. To produce group feedback information
of a number of students working on a particular
course is given to the author of the course. Using
this information, an author may be able to optimize
his/her course.
5 FEEDBACK GENERATION TO
AUTHOR
In order to help the author prepare teaching material
efficiently, Authoring Tool provides task ontology
for workflow. When the goal of training is for
example to teach the operator how to recover from
an accident, the training procedure is a sequence of
recognition, judgment and actions. This sequence is
called a workflow.
AUTOMATIC FEEDBACK GENERATION - Using Ontology in an Intelligent Tutoring System for both Learner and
Author Based on Student Model
119

Corresponding to each specific mistake, the
author has a teaching strategy in his mind. With
training task ontology, he models his strategy into a
sequence of teaching behaviors. The modeling
process is made up of two levels: the first is to
model the knowledge in his mind into a sequence of
abstract steps (sub-tasks). The second is to model the
subtasks to a sequence of concrete teaching actions
on teaching materials.
With the goal of making the student recognize an
error, the procedure usually includes the following
six steps:
1) teaching the student to recognize the
existence of an error
2) teaching the student the cause of the error
3) giving further explanation about the error
4) teaching underlying knowledge for deep
understanding
5) giving explanations on the contradiction in
the student’s answer
6) pointing out the error directly
At a relatively higher level, teaching strategies
are modeled into frameworks with goals and sub-
goals. Along with the sub-goals in the author’s
mental agenda are teaching behaviors with materials
such as concrete examples, hints, demonstrations
and simulations to be used to attain the sub-goals.
As the sub-goals become concrete, they finally can
correspond to a sequence of teaching behaviors. But
how to help the author to represent the behaviors is
still a difficult problem. We need a facility to model
these behaviors, and that is the training task
ontology we are developing. In the training task
ontology, we define vocabulary, which can be used
by the author to represent his/her behaviors
explicitly. With the help of the training task
ontology, the author can model his/her teaching
behaviors into a series of verb-object phrases.
Furthermore, the author arranges the teaching
materials according to such behaviors, in order to get
a sequence of well-arranged material which will be
shown to the students.
To determine the quality of a course, we want to
detect whether or not the following properties hold
for a course. If such a property holds, this may
signal (the absence of) a potential mistake:
• Completeness: Are all concepts that are used
in the course defined somewhere?
• Timely: Are all concepts used in a course
defined on time?
• Recursive concepts: Are there concepts
defined in terms of it self?
• Correctness: Does the definition of a concept
used in the course correspond to the definition of the
concept in the ontology?
• Synonyms: Are there concepts with different
names but exactly the same definition?
• Homonyms: Are there concepts with multiple,
different definitions?
Since a course and course related material are
represented by means of schema languages such as
RDF, we can use schema analysis techniques to
answer the above questions, and to produce
feedback about possible mistakes for authors. We
have implemented the mentioned analyses as six
distinct schema-analyses, which we show at work in
simple course structure and domain ontology.
6 SCHEMA ANALYSIS AND THE
REASONING RULES TO
DETERMINE FEEDBACKS
As we mentioned, the domain ontology represents
by RDF and the course structure is modified by
XML. So use of these tools facilitates the reasoning
process and sharing information between different
types of components. We used from Description
Logic as method for ontology reasoning and we
generate feedbacks by this means.
Description Logic (DL) allows specifying a
terminological hierarchy using a restricted set of first
order formula. The equivalence of OWL (Ontology
Web Language, like RDF) and DL allows OWL to
exploit the considerable existing body of DL
reasoning fulfill important logical requirements.
These requirements include concept satisfiability,
class subsumption, class consistency, and instance
checking. Table 1 shows a subset of reasoning rules
that support OWL entailed semantics.
Table 1: Parts of OWL reasoning rules.
TransitiveProperty
(?P rdf:type owl:TransitiveProperty)
^ (?A ?P ?B) ^ (?B ?P ?C) Î(?A ?P
?C)
subClassOf
(?a rdfs:subClassOf ?b) ^ (?b
rdfs:subClassOf ?c) Î(?a
rdfs:subClassOf ?c)
subPropertyOf
(?a rdfs: subPropertyOf ?b) ^ (?b
rdfs: subPropertyOf ?c)
Î(?a rdfs: subPropertyOf ?c)
disjointWith
(?C owl:disjointWith ?D) ^ (?X
rdf:type ?C) ^ (?Y rdf:type ?D)
Î(?X owl:differentFrom ?Y)
inverseOf
(?P owl:inverseOf ?Q) ^ (?X ?P ?Y)
Î(?Y ?Q ?X)
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
120

We used the above reasoning for feedback
generation to student from his/her student model.
For detecting authoring problems, we used Schema
analysis. Schema analysis techniques are based,
amongst others, on mathematical results about fixed
points. Since these results are not widely known, we
will explicitly show how to use them in the context
of schema analyses. Schema analyses will be
expressed in the functional, declarative,
programming language Haskell; since this allows us
to stay close to the mathematical results we use
(Haskell, 2005). We give some examples of schema-
analyses that determine whether or not certain
properties hold. The results of these analyses form
the basis of feedback to the author. The analyses
take the schemata as input. In this paper we perform
two types of analyses: 1) the analysis of structural
properties of a schema, for example the recursive
property, and 2) the comparison of a schema with
one or more other schemata, for example to test the
correctness of a definition.
6.1 Solving Authoring Problems
with Schema Analysis
In this section we describe six algorithms (four
briefly and two in more detail), which can be used to
signal the (possible) mistakes listed in section 5.
Completeness − we distinguish three kinds of
(in) completeness: (1) within a course, (2) within
domain ontology and (3) between a course and
domain ontology. If a concept is used in a course,
for example in a definition or an example, it has to
be defined elsewhere in the course. The undefined
concepts in a course are calculated in three steps: (1)
determine the set of concept id’s that appear in the
right- and left hand sides of concepts within
examples and all concept id’s that appear in the right
hand side of concepts within definitions (used
concepts), (2) determine the concept id’s that appear
in the left-hand side of concepts in definitions
(defined concepts) and (3) check that each of the
used concepts appears in the set of defined concepts.
A course is complete if all concepts used appear in
the set of defined concepts. Completeness can also
be applied to (domain) ontology, and between a
course and ontology. The first one check whether all
used concepts in the ontology are defined in the
same ontology, the second one if all used concepts
in a course are defined in the ontology. The same
three steps are performed in both functions.
Timely − A concept can be used before it is
defined. This might not be an error if the author uses
an inductive instead of a deductive strategy to
teaching, but issuing a warning is probably helpful.
Furthermore, there may be a large distance
(measured for example in number of pages,
characters or concepts) between the definition and
the use of the concept, which is probably an error.
We define the function timely to determine whether
or not concepts in a course are defined in time and a
function outOfOrderConcepts to list the concepts
that appear to be out of order.
timely::Course → Bool
timely = null.outOfOrderConcepts
In function outOfOrderConcepts, function
extractActivities returns for every activity in the
course the tuple (Strategy, [Extra_p]) and puts these
tuples in a list activities. Then, using functions inits
and tails every [Extra_p] list is split as follows: for
every element x in the list [Extra_p] the list is
subdivided into a left part (epl), which contains all
elements to the left of element x, and a right part
(epr), which contains element x as and all elements
to the right of x. For example, for the input list [e, d]
we get [([], [e, d]), ([e], [d]), ([e, d], [])], where e is
example and d is definition. Finally, function intime
tests the timely constrains for all tuples (es, (epl,
epr)): if the first element of epr is a definition and
the educational strategy is deductive, then: 1) a
related example appears after the definition, and 2)
no related example appears before the definition
(tested by elemBy eqConcept c in the code below).
In case of an inductive activity, a related example
appears before the definition and no related example
appears after the definition. Function intime is
always true if epr is empty or the first element of epr
is an example.
outOfOrderConcepts::Course → [Extra_p]
outOfOrderConcepts c =
let activities = extractActivities c
split = [(es, s) | (es, eps) <-
activities, s <- zip (inits eps) (tails
eps)]
in [head epr | (es, (epl, epr)) ←
split, not (intime (es, epl, epr))]
intime (_, _, []) = True
intime (_, _, Ex (j, c, cs, r) :_) =
True
intime (Deductive, epl, Def (j, c, cs):
epr) = elemBy eqConcept c epr && not
(elemBy eqConcept c epl)
intime (Inductive, epl, Def (j, c, cs):
epr) = elemBy eqConcept c epl && not
(elemBy eqConcept c epr)
eqConcept id (Def (i, c, cs)) = False
eqConcept id(Ex(i, c, cs, r)) = id == c
Recursive concepts − A concept can be defined
in terms of itself. Recursive concepts are often not
desirable. If a concept is recursive, there should be a
AUTOMATIC FEEDBACK GENERATION - Using Ontology in an Intelligent Tutoring System for both Learner and
Author Based on Student Model
121

base case that is not recursive. Recursive concepts
may occur in a course as well as in ontology. We
define two functions: recursiveOntology and
recursiveCourse which take ontology respectively a
course as argument. Both first extract all concept
definitions, and use function recursiveConcepts. We
show the definition of recursiveOntology.
recursiveOntology::Ontology → Bool
recursiveOntology =
not.null.listRecursiveConceptsOntology
listRecursiveConceptsOntology::
Ontology → [Id]
listRecursiveConceptsOntology =
recursiveConcepts.xtractAllConceptsOnt
Function recursiveConcepts calculates for every
concept all reachable concepts. Every concept in
reachables is checked for recursiveness: a concept is
recursive if the concept’s Id is a member of the set
of reachable concepts. The recursive concepts are
collected in a list.
recursiveConcepts::
[(Id, RelatedConcepts)] → [Id]
recursiveConcepts allConcepts =
let nonTerminalConcepts =
filter (not. null. snd) allConcepts
reachables = reachable
nonTerminalConcepts allConcepts
in [x |(x, y) ← reachables, elem x y]
Synonyms − Concepts with different names may
have exactly the same definition. For example,
concept a, with concept definition (a, [c, d]), and
concept b, with concept definition (b, [c, d]), are
synonyms. In general, given a set productions, two
concepts x and y are synonyms if their identifiers are
different, Id
x
≠Id
y
, and (reachableTerminals
productions x) equals (reachableTerminals
productions y).
We define function synonyms to check for
synonyms in ontology: for all concepts in the
ontology all reachable terminal concepts are
determined. Concepts with the same reachable
terminal concepts and different concept id’s are
collected in a list.
Homonyms − A concept may have multiple,
different definitions. If for example concept “a” has
definitions (a, [b, c]) and (a, [d, f]), then these two
definitions are homonyms. To list the homonyms in
an ontology, we calculate the concepts that appear at
least twice in the left hand side of a definition.
Correctness − the concepts in a course should
correspond to the same concepts in its domain
ontology. To determine whether or not this is the
case, for every concept in a course all reachable
terminal concepts are determined by function
reachableTerminals. The set of productions contains
the course’s concepts completed with the concepts
of the ontology for concepts that are not defined in
the course. The result of this calculation is compared
against the reachable terminal concepts of the same
concept defined in the ontology.
7 CONCLUSION
Feedback is crucial in education: it is an essential
element needed for effective learning. Semantically
rich feedback is sparse in most eLearning systems.
In this paper we present our ideas about an
Intelligent Tutoring system that produces
semantically rich feedback for learners as well as for
authors. The system we imagine consists of a
generic feedback engine: different ontologies can be
plugged in, i.e. they are the arguments of the
feedback engine. This is important because
mechanisms for automatically generating feedback
are involved, and should be reused for different
ontologies. The system supports the generation of
generic as well as domain specific feedback.
The most important aspect of this idea is that it
uses student model and its features that we
considered in it for better automatic feedback
generation. We defined feedback patterns based on
ontologies for educational elements such as certain
types of questions, examples, definitions, etc. So all
the parts of this designed system is ontology based.
REFERENCES
Aroyo, L., Dicheva, D., 2004. Authoring support in
concept-based web information systems for
educational applications, in Int. J. Cont. Engineering
Education and Lifelong Learning, Vol. 14, No. 3.
Aroyo, L., Dicheva, D., 2004. The new challenges for e-
learning: The educational semantic web, Educational
technology & Society, 7 (4), 59 – 69.
Aroyo, L., Mizoguchi, R., 2004. Towards Evolutional
authoring support systems, Journal of interactive
learning research 15(4), 365-387, AACE, USA.
Brickley, D., Guha, R.V., 1999. Resource Description
Framework (RDF) Schema Specification. Proposed
Recommendation, World Wide Web Consortium:
http://www.w3.org/TR/PR-rdf-schema.
Brusilovsky, P., 1994. The construction and application of
student models in intelligent tutoring systems. Journal
of Computer and System Sciences International, 32(1),
70-89.
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
122

Brusilovsky, P., 2003. Developing adaptive educational
hypermedia systems: From design models to authoring
tools. In: T. Murray, S. Blessing and S. Ainsworth
(eds.): Authoring Tools for Advanced Technology
Learning Environment. Dordrecht: Kluwer Academic
Publishers, 377-409.
Cristea, A., 2004. Authoring of Adaptive Hypermedia:
Adaptive Hypermedia and Learning Environments,
book chapter in "Advances in Web-based Education:
Personalized Learning Environments", Sherry Y. Chen
and Dr. George D. Magoulas. IDEA publishing group.
Davey, B., Priestly, H., 2001. Introduction to lattices and
order, 2nd
edition, Cambridge University Press.
Haskell, 2005. http://www.haskell.org
Hendler, J., McGuinness, D.L., 2000. The DARPA Agent
Markup Language. IEEE Intelligent Systems 16(6): 67
- 73.
Holt, P., 1994. The state of student modeling, In: Greer,
G., McCalla, G. Eds. Student Modelling: The Key to
Individualized Knowledge-Based Instruction, Spring -
Verlag, 3-35.
Ikeda, M., et al., 1997. Task ontology makes it easier to
use authoring tools, In: Proc. Of IJCAI’97, Nagoya,
342 -347.
Jeuring, J., Swierstra, D., 1995. Constructing functional
programs for grammar analysis problems, In
Conference Record of FPCA '95, SIGPLAN-
SIGARCH-WG2.8 Conference on Functional
Programming Languages and Computer Architecture,
pages 259 - 269.
Jin, L., et al., 1997. Role explication of simulation in
intelligent training systems by training task ontology.
In: Proc. Of AIED97.
Jin, L., Chen, W., Hayashi, Y., Ikeda, M., Mizoguchi, R.,
1999.An ontology-aware authoring tool, Artificial
intelligence in Education, IOS Press.
Lane, C., 1998. Gardner’s multiple Intelligence.
http://www.tecweb.org/eddevel/gardner.html.
Lane, C., 2000. Learning styles and multiple intelligences
in distributed learning/IMS projects. 31 Segovia, San
Clemente, CA 92672 (949) 369-386, The Education
Coalition (TEC).
Mizoguchi, R., et al., 1992. Task ontology and intelligent
training system use in a task analysis interview
system--Two-level mediating representation in
MULTIS. In: Proc. Of the JKAW92, 185-198.
Mizoguchi, R., et al., 1995. Ontology for modeling the
world from problem solving perspectives, In: Proc. Of
IJCAI Workshop on Basic Ontological Issues in
Knowledge sharing, Montreal.
Murray, T., 1998. Authoring knowledge base tutors: tools
for content, instructional strategy, Student Model, and
Interface Design. J. Of the Learning Sciences, 7, 1, 5-
64.
Murray, T., 1999. Authoring intelligent tutoring systems:
An analysis of the state of the art. International Journal
of AI in education, 10, 98 - 129.
Passier, H., Jeuring, J., 2004. Ontology based feedback
generation in design-oriented e-learning systems,
Proceedings of the IADIS International Conference-
Society 2004, Avila, Spain.
Russell, S, Norvig, P., 1995.Artificial intelligence, A
modern approach, Prentice Hall Int. editions.
Shute, V.J., 1995. SMART: student modeling approach for
responsive tutoring. User Modeling and User-Adapted
Interactions 5: 1-44, Kluwer Academic Publisher.
Stojanovic, L., Staab, S., Studer, R., 2001. ELearning
based on the semantic web, in WebNet 2001 – World
conference on the www and internet, Orlando, Florida,
USA.
AUTOMATIC FEEDBACK GENERATION - Using Ontology in an Intelligent Tutoring System for both Learner and
Author Based on Student Model
123
