Improved Singular Value Decomposition for Supervised

Learning in a High Dimensional Dataset

Ricco Rakotomalala

and Faouzi Mhamdi

ERIC Laboratory - University of Lyon 2

Bron, France

URPAH - University of Tunis

Tunis, Tunisie

Abstract. Singular Value Decomposition (SVD) is a useful technique for di-

mensionality reduction with a controlled loss of information. This paper makes

the very simple but worth-while observation that many attributes that contain no

information about the class label, may thus be selected erroneously for a super-

vised learning task. We propose to ﬁrst use a very tolerant ﬁlter to select on a

univariate basis which attributes to include in the subsequent SVD. The features,

“the latent variables”, extracted from relevant descriptors allow to build a better

classiﬁer with a signiﬁcant improvement of the generalization error rate and less

cpu time. We show the efﬁciency of this combination of feature selection and

construction approaches on a protein classiﬁcation context.

1 Introduction

Data preprocessing is a crucial step when we have to analyze an unstructured dataset.

Indeed, it is not possible to handle directly the native description of data to run a ma-

chine learning algorithm when we treat images, text, or in our case, when we want to

predict proteins families from their primary structure. The learning process is thus pre-

ceded by two data preprocessing operations: extract descriptors from the native format

of data in order to build an attribute value table; build features from these descriptors in

order to produce an efﬁcient classiﬁer

The direct use of all descriptors extracted from the unstructured representation as

features for the learning algorithm is in general not a good strategy. Their number is

very high, which induces drawbacks: the computing time is very high and the quality of

the learning classiﬁer is often poor because we have a sparse dataset, and it is difﬁcult

to estimate in a reliable way the probability distribution (”The curse of Dimensionality

Problem”). In a protein discrimination process from their primary structures [1], the

native description of a protein is a succession of characters representing amino acids.

It is not possible to run directly a learning algorithm. We then generated a Boolean

In this paper, we call ”descriptors” the attributes which are extracted from the native data

format, i.e., n-grams in our context; we call ”features” the attributes which are presented to

the supervised learning algorithm.

Rakotomalala R. and Mhamdi F. (2006).

Improved Singular Value Decomposition for Supervised Learning in a High Dimensional Dataset.

In 6th International Workshop on Pattern Recognition in Information Systems, pages 38-47

DOI: 10.5220/0002472600380047

 SciTePress

attribute-value table by checking the presence or absence of 3-grams (a sequence of

3 consecutive characters) for each protein. Because there are 20 kinds of characters

(amino acids), we can produce 8000 descriptors for 100 examples, the quality of the

classiﬁer on all descriptors is often bad.

To solve these disadvantages, we are interested in the creation of intermediate fea-

tures from the descriptors. The goal is to produce a new representation space which

preserves the properties of the initial space, in particular by preserving the proximity

between the examples. These new features, which will be provided to the learning al-

gorithm, must have the following qualities: they must represent a good summary of the

original data; they must be easy to interpret so that we can understand the inﬂuence of

each descriptors; they must be relevant for a supervised learning task; a small number

of them must be sufﬁcient to learn classiﬁer efﬁciently. The singular value decomposi-

tion (SVD) seems to answer in an adequate way these speciﬁcations. Indeed it aims to

transform raw data to a new co-ordinate system, where the axes of the new space repre-

sent “factors” or “latent variables” which reveal the underlying structure of the dataset.

This approach, very popular in high dimensional data processing, presents nevertheless

a drawback in the context of supervised learning: a lot of initial descriptors are irrele-

vant for the supervised learning task. To take them into account in the construction of

features (factors) considerably reduced the relevance of these features.

In this paper, we propose to insert a phase of descriptor selection before building

the latent variables with the singular value decomposition. This phase of selection must

only take account of the relevance of the descriptors and not of their redundancy, it

must be rather permissive so that information necessary to discriminate is preserved.

Only the selected descriptors will then be presented to the SVD, thus making it possi-

ble to produce an effective reduced space of representation for discrimination. In our

protein discrimination context, the results show that it is sufﬁcient to keep 5 factors.

Another advantage, although that was not our ﬁrst goal in this work, is that the reduc-

tion of the number of descriptors presented to the SVD algorithm allows one to reduce

dramatically the computing time.

Section 2 introduces the SVD process and our improvement in the context of su-

pervised learning in high dimensional dataset. The protein discrimination problem and

results of experiments are presented in Section 3. Section 4 describes some further ex-

periments which allows us to better evaluate the behavior of our approach. We conclude

in Section 5.

2 The Singular Value Decomposition for Supervised Learning

2.1 The Singular Value Decomposition Process

SVD produces a new representation space of the observations starting from the ini-

tial descriptors by preserving the proximity between the examples. These new features

known as ”factors” or ”latent variables” have several very advantageous properties: (a)

their interpretation very often allows to detect patterns in the initial space; (b) a very

reduced number of factors allows to restore information contained in the data; (c) the

new features form an orthogonal basis, learning algorithms such as linear discriminant

analysis work well [2]. This process is often used in microarray data analysis [3] or text

retrieval [4], ﬁelds where the initial number of descriptors is very high and where the

dimensionality reduction is crucial before data analysis.

There are numerous theoretical presentations of the SVD. Roughly speaking, we

produce from an initial description space ℵ = {X

, . . . , X

} of J descriptors (and n

examples), a new space of J features Ψ = {F

, . . . , F

} with the following constraints:

Ψ is an orthogonal basis; the factor F

is built from a projection vector P

(kP

k = 1)

so as to maximize the variance of F

, v

= Var (F

); the second factor F

is built from

a projection vector P

(kP

k = 1) so as to maximize the variance v

= Var (F

), and

must be independent (perpendicular) to F

, etc. In the two spaces, the proximity

between two individuals is preserved, and more interesting, in the subspace p (p <

J) of Ψ, the distance between two examples is roughly respected, the quality of the

approximation can be measured using the sum of variance of p ﬁrst selected factors

j=1

There is a mathematical relation between SVD and PCA (Principal Component

Analysis) when the descriptors are standardized. If ℵ

′

is the transpose of ℵ, the square

matrix (ℵ

′

ℵ) is a correlation matrix: v

is its ﬁrst eigenvalue and P

is the associated

eigenvector. Thus, the sum of variance of the ﬁrst p selected factors is the proportion of

explained variance with these factors (E

In addition to the dimensionality reduction which improves the efﬁciency of the

supervised learning algorithm, this process allows to detect and extract the true patterns

in the data, the last factors express the noisy information in the dataset. From this point

of view, the SVD is an effective data cleaning process, by selecting the p best factors,

we reject negligible information contained in the data. Thus, it is possible to reconstruct

an approximate version of original data from the selected factors and projection vectors.

About the implementation, the challenge was considerable. It was not possible to

use diagonalization techniques from the 8000 × 8000 correlation matrix in order to

extract eigenvalue and eigenvectors. It was thus necessary to consider the direct extrac-

tion of the singular values from the standardized matrix ℵ with a powerful algorithm,

the computing time and the memory requirement are major constraints. We used the NI-

PALS implementation [5] which interprets the singular value extraction as successive

orthogonal regressions: the ﬁrst one produces the ﬁrst factor F

, using the residuals of

this regression, we perform a new regression in order to produce the second factor F

etc. This approach allows to reduce computations considerably since we can stop calcu-

lations as soon as the ﬁrst p factors were generated. In our experiments, from a n = 100

examples and J = 7000 descriptors, the ﬁrst 5 factors are generated in 10 seconds on

a standard personal computer running under Windows (Pentium III – 1 Ghz – 512 MB

RAM). We use the TANAGRA [6], an open source data mining software, source code

is available on the website of the authors (http:\\eric.univ-lyon2.fr\˜ricco\tanagra).

2.2 SVD and Irrelevant Descriptors

If the SVD is a very interesting process for dimensionality reduction by controlling the

loss of information, it has a major drawback in a protein classiﬁcation framework: the

SVD is an unsupervised process. In fact, to build the factors, it used all the descriptors,

including the irrelevant one for a supervised learning task.

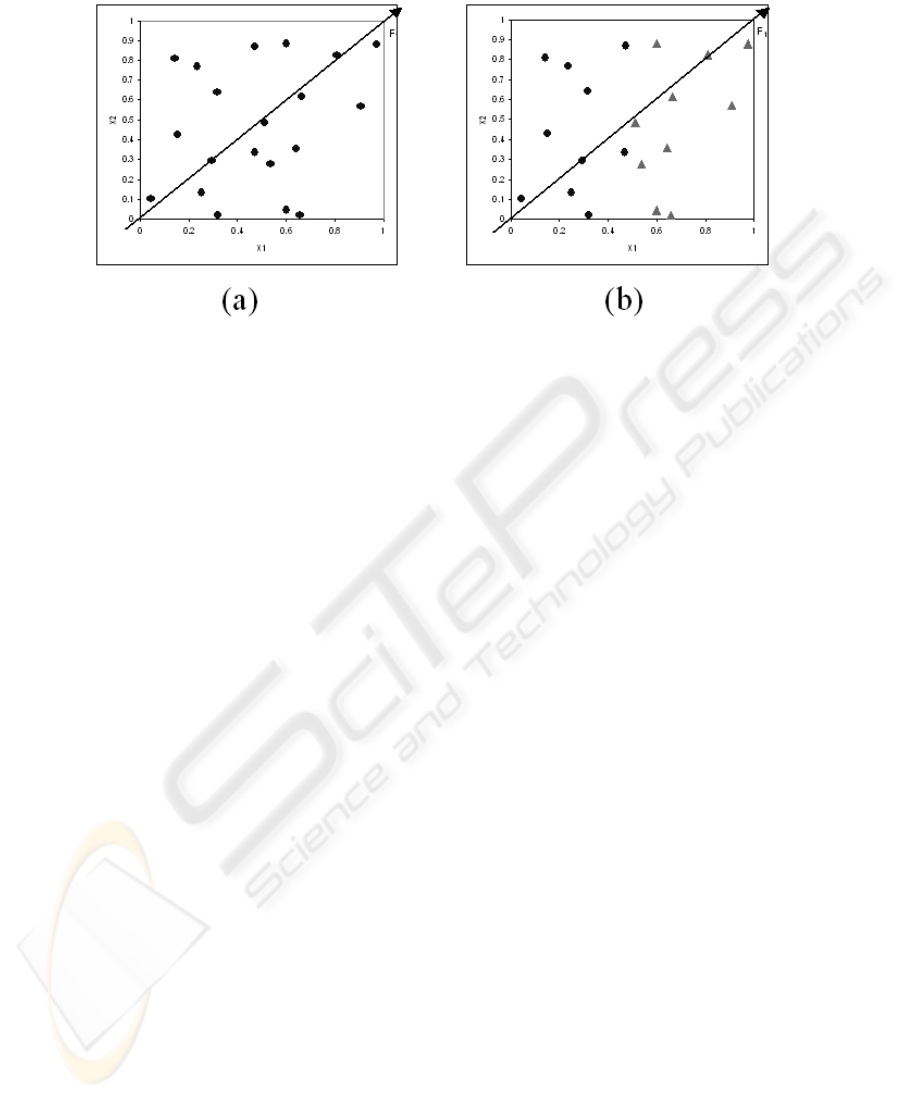
Fig.1. SVD on unsupervised (a) and supervised (b) tasks.

To illustrate this drawback, we show the same situation on an artiﬁcial two-dimen–

sional dataset (Figure 1). On the unlabeled dataset (Figure 1.a), the ﬁrst extracted factor

seems appropriate, but on the labeled dataset (Figure 1.b), we see that the descriptor

is irrelevant for the learning task, however the SVD extracts the same factor F

In this paper, we propose to perform ﬁrst a descriptor selection before building

the factors with SVD. We call this combination FS-SVD (Feature Selection - Singular

Value Decomposition). The goal of the selection is not to produce the most powerful

subspace for the prediction like in classical feature selection process [7] but rather to

eliminate the irrelevant descriptors before the SVD process. In this point of view, we

use a very simple ﬁlter algorithm: we rank the descriptors according to the correlation

coefﬁcient criterion and keep the 50 best for SVD (the correlation coefﬁcient computed

on 0/1 attribute is similar to χ

criterion on Boolean true/false attribute) [8]. Of course,

some selected descriptors are redundant but it is does not matter because the features

obtained with the SVD are orthogonal.

We propose the following framework for protein classiﬁcation:

– Extract descriptors from native format of proteins sequences;

– Select the 50 most correlated descriptors with the class-attribute (protein family);

– Build and select the 5 ﬁrst (best) features with the SVD process;

– Use these features in a supervised learning algorithm, we use a nearest neighbor

classiﬁer (3-NN) because it is very sensitive to irrelevant descriptors and allows

us to evaluate our data preprocessing framework, especially the preservation of

the proximity between the examples [2]. We plan to test other supervised learning

algorithms in the near future.

The chosen parameters in our study (50 descriptors and 5 features) are deﬁned in

an approximate way and are appropriate for all cases that we treated. Actually, in the

majority of cases, the ﬁrst 2 factors are sufﬁcient, but we preferred to make a simpli-

ﬁed choice and avoid ﬁne tuning parameters which is always problem dependent and a

Fig.2. Native description of proteins.

source of overﬁtting, especially when we use a cross validation error rate estimate. This

is particularly true in our case where we have a small number of examples compared to

a large number of descriptors.

3 Experiments on a Protein Classiﬁcation Problem

3.1 The Protein Classiﬁcation Problem

In this paper, we use the text mining framework for a protein classiﬁcation problem

from their primary structures. The analogy with text classiﬁcation is relevant in our case,

indeed the original description of the dataset is very similar. A protein is described by

a series of characters which represents amino acids. There are 20 possible amino acids.

We show an example of a ﬁle describing a few proteins (Figure 2).

However, unlike the text classiﬁcation, there is no ”natural” separation in the char-

acter sequences, it is not possible to extract ”words” for which we can easily attach

semantics properties. Therefore, we have used the n-grams, a sequence of n consecu-

tive characters, in order to produce descriptors.

Previous works showed that the choice of n = 3 (3-grams) and boolean descriptors

give a good compromise to produce accurate classiﬁer [1]. We obtain a Boolean at-

tribute - value dataset with several thousands of descriptors (Figure 3). The theoretical

maximum number of 3-grams for a protein classiﬁcation problem is 20

= 8000. Of

course, all 3-grams are not present in a dataset but experiments showed that we were

close to this value. Numerous of 3-grams are irrelevant, others also are redundant. The

main challenge of the feature reduction is to build appropriate features for a supervised

learning task. There are several reasons for this dimensionality reduction: (1) machine

learning algorithms work badly when the dataset is too sparse; selecting a subset of

relevant features often improves the classiﬁer performance; (2) the complexity of the

learning algorithms always depends on the number of input features; the elimination

of useless attributes allows to a considerable improvement in computing time; (3) a

reduced number of features provides a better understanding of the classiﬁer.

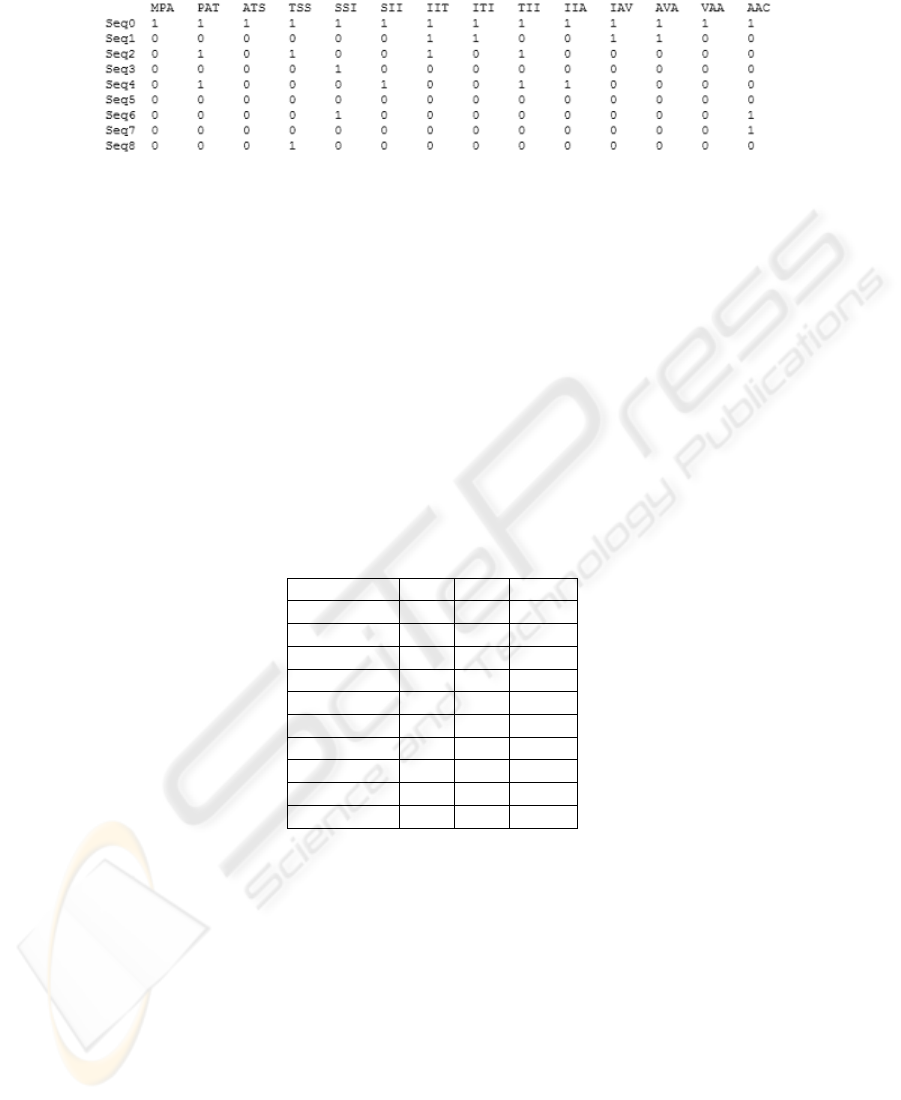
Fig.3. Boolean 3-grams attribute-value table from native description.

3.2 Experimental Results

Five protein families have been randomly extracted from the data bank SCOP [9], the

aim being to discriminate each pair of proteins. We use the bootstrap-plus error rate

estimate [10] instead of the standard cross-validation or leave-one out error rate estimate

because they can suffer of high-variability in certain cases.

In this paper, we compare 3 approaches: (ALL) we run the nearest neighbor al-

gorithm on all descriptors; (SVD) we run the learning algorithm on the 5 ﬁrst factors

extracted from all descriptors; (FS-SVD) we perform a selection of 50 best descriptors

and run the learning algorithm on the 5 ﬁrst factors extracted using a SVD from these

descriptors. The results are available in Table 1.

Table 1. Estimated error rate on each protein discrimination problem.

Proteins pairs ALL SVD FS-SVD

0.1778 0.0445 0.0024

0.1728 0.0015 0.0045

0.1293 0.0189 0.0035

0.1664 0.0083 0.0019

0.2593 0.1653 0.0308

0.1113 0.0731 0.0276

0.1496 0.1301 0.0213

0.2073 0.0805 0.0310

0.2328 0.1111 0.0568

0.1441 0.1685 0.0387

The results suggest some interesting comments:

– Running the learning algorithm on all descriptors is an inefﬁcient approach, the

high dimensionality deteriorates the results, because there are many irrelevant de-

scriptors, but also because the nearest neighbor works poorly when we have a sparse

dataset.

– The SVD approach improves the performance of the classiﬁer, the dimensionality

reduction allows the learning algorithm to work well. Let us note that in the ma-

jority of the problems studied, the ﬁrst 5 factors restore 15% of the information

contained in the data. We will further study below the inﬂuence of the number of

selected factors on the performance of the classiﬁer.

– Descriptor selection before building the factors is an efﬁcient way to improve the

classiﬁer performance. In all cases, FS-SVD outperforms SVD, removing irrelevant

descriptors helps the singular value decomposition technique to build more relevant

features (factors) for the learning algorithm.

Even if that were not our ﬁrst goal in this work, it nevertheless were interesting

to compare the computing times between the two approaches (SVD and FS-SVD): we

noted that, on average, the descriptor selection allows to reduce 15 times the execution

time of the protein classiﬁcation problems.

4 Discussion: Further Experiments

4.1 The Inﬂuence of the Number of Factors

On the FS-SVD process, a detailed study of the results showed that very often the ﬁrst

2 factors are sufﬁcient to produce powerful classiﬁer. We can use a feature selection

process to individually evaluate each factors. Because they are orthogonal, an evaluation

of their relevance can be independently used but we think that it is not decisive in our

case, this is why we make the default choice of 5 factors.

More interesting was the choice of the number of factors for the SVD process. The

choice of 5 factors allows us to compare the two approaches but we have seen that in

this case, the loss of information is nevertheless signiﬁcant. For the F

problem (Table

1) , we set several values of extracted factors with the SVD approach, we measure the

explained variance and the error rate of the learning classiﬁer (Table 2). We see that the

trade-off between the quality of the representation (explained variance on the selected

factors) and efﬁciency of the learning algorithm (which suffers of the increase of the

representation space) is not easy to ﬁnd. To introduce a ﬁne adjustment of the number

of selected factors in order to optimize the error rate is at the opposite of our approach,

moreover that would increase the risks of overﬁtting.

Table 2. Explained variance and error rate of the classiﬁer for the F

problem.

Selected factors (%) variance Error rate

5 15 0.0805

10 24 0.0801

20 38 0.1100

50 67 0.2063

100 95 0.2129

4.2 Feature Construction vs. Feature Selection

Select relevant and non redundant features leads to improved classiﬁcation accuracy.

In this paper, the descriptor ranking allows to eliminate irrelevant descriptors, the SVD

process allows to build orthogonal features from the relevant descriptors.

In order to improve the classiﬁer performance, another solution is to perform a more

aggressive descriptor selection which combines the detection of the relevance and the

elimination of redundancy. The correlation based approach seems a promising way in

this domain, especially in the microarray data analysis. The FCBF method [11] can

make the best trade-off between relevance and redundancy. It is important in this paper

to verify, in the ﬁrst time, if this approach leads to better classiﬁer, and in the second

time, to consider the respective advantage of the two approaches, feature construction

from SVD and redundancy based descriptor selection.

Table 3. Number of the selected descriptors and error rate with FCBF. Comparison with FS-SVD.

Proteins pairs Err. (FS-SVD) Descriptors (FCBF) Err. (FCBF)

0.0024 28 0.0048

0.0045 30 0.0022

0.0035 30 0.0028

0.0019 23 0.0020

0.0308 5 0.0476

0.0276 13 0.0272

0.0213 6 0.0702

0.0310 9 0.0376

0.0568 6 0.0649

0.0387 12 0.0262

Roughly speaking, FCFB ranks the features using a correlation measurement. It

selects a feature (1) if its correlation with class attribute is upper than δ (a parameter

of the algorithm); (2) if it is predominant i.e. its correlation with the class attribute is

upper than its cross-correlation to the all other features. In our experiment, it is clear that

FCBF is heavily parameter dependent. The δ parameter which allows to control the size

of selected descriptors subset is very hard to adjust. We use the standard δ = 0.3 which

seems a good compromise for our ﬁles, experiments results are reported in Table 3. It

seems that FCBF gives similar results to our approach, in 4 dataset FCBF outperforms

FS-SVD, the dimensionality reduction is effective. It is even possible to obtain better

results by adjusting the parameter; in this case, the number of selected descriptors can

be modiﬁed without signiﬁcant improvement of the classiﬁer performance.

But a detailed study of the results calls into question theses results. Indeed, in our

dataset the descriptors are automatically generated from an unstructured data format,

the choice of 3-grams is a compromise in order to obtain a efﬁcient classiﬁer, the elim-

ination of the redundant descriptors is a purely mechanical process, it masks the con-

comitant action of two or several descriptors. For instance, for the discrimination of

”Tool Like Receptor” protein family, experts know that the 4-gram ”LDLS” is a signiﬁ-

cant descriptor. Because we use 3-grams, we obtain ”LDL” and ”DLS”, the redundancy

based methods eliminates one of them, thus preventing any thorough interpretation of

the results.

The SVD offers several kind of visualization of the results. Its advantages in protein

discrimination are interesting: we can at the same time study our data as well from the

point of view of the coordinate of individuals in the new representation space, as the

point of view of the evaluation of the inﬂuences of the descriptors in the construction

of the ”latent variables”. This ”pattern detection” property of SVD can be very useful

in the search of more powerful and interpretable descriptors than the simple 3-grams.

We can for instance build a 4-grams from 2 compatibles 3-grams which are highly

correlated with the ﬁrst factor. We manually did it for the moment, but it appears that it

is a promising approach if we ﬁnd a strategy to automatize this process.

5 Conclusion

In this paper we show that elimination of irrelevant descriptors allows the singular value

decomposition to produce more efﬁcient factors for the protein classiﬁcation context

where we have a high dimensional boolean dataset. The classiﬁer accuracy is improved

signiﬁcantly. In the same time, the computing time is dramatically reduced. Our ap-

proach is rather robust because we can avoid any ﬁne tuning of the parameters, the risks

of overﬁtting are reduced.

These results open new perspectives. Indeed, the singular value decomposition of-

fers powerful tools for interpretation of results which make it possible for the expert to

improve his knowledge of the domain and to propose some explorations which can, in

particular, lead to the creation of more powerful and understandable descriptors.

In this paper, we see that combining feature selection and SVD allows to increase

the performances of K-NN which is very sensitive to high dimensionality. In a future

work, it will be interesting to study the behavior of this data processing on more robust

learning algorithms such as linear support vector machine and try to characterize the

context where this approach is the most powerful.

References

1. Mhamdi, F., Elloumi, M., Rakotomalala, R.: Text-mining, feature selection and data-mining

for proteins classiﬁcation. In: Proceedings of International Conference on Information and

Communication Technologies: From Theory to Applications, IEEE Press (2004) 457–458

2. Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining,

Inference, and Prediction. Springer (2001)

3. Wall, M., Rechtsteiner, A., Rocha, L.: Singular Value Decomposition and Principal Com-

ponent Analysis. In: A Practical Approach to Microarray Data Analysis. Kluwer (2003)

91–109

4. Husbands, P., Simon, H., Ding, C.: On the use of the singular value decomposition for

text retrieval. In: Proceedings of 1st SIAM Computational Information Retrieval Workshop.

(2000)

5. Wold, S., Esbensen, K., Geladi, P.: Pricnipal component analysis. Chemometrics and Intel-

ligent Laboratory Systems 2 (1987) 37–52

6. Rakotomalala, R.: Tanagra: une plate-forme d’exp

erimentation pour la fouille de donn

ees.

Revue MODULAD (2005) 70–85

7. Guyon, I., Elisseeff, A.: An introduction to variable and feature selection. Journal of Machine

Learning Research 3 (2003) 1157–1182

8. Duch, W., Wieczorek, T., Biesiada, J., Blachnik, M.: Comparison of feature ranking methods

based on information entropy. In: Proceedings of International Joint Conference on Neural

Networks (IJCNN), IEEE Press (2004) 1415–1420

9. Murzin, A., Brenner, S., Hubbard, T., Chothia, C.: Scop: a structural classiﬁcation of proteins

database for the investigation of sequences and structures. Journal of Molecular Biology

(1995) 536–540

10. Efron, B., Tibshirani, R.: Improvements on cross-validation: The 0.632+ bootstrap method.

JASA 92 (1997) 548–560

11. Yu, L., Liu, H.: Redundancy based feature selection for microarray data. In: KDD ’04:

Proceedings of the 2004 ACM SIGKDD international conference on Knowledge discovery

and data mining, New York, NY, USA, ACM Press (2004) 737–742