How Style Checking Can Improve

Business Process Models

Volker Gruhn and Ralf Laue

Chair of Applied Telematics / e-Business

⋆

Computer Science Faculty, University of Leipzig, Germany

Abstract. Business process analysts prefer to build business process models

(BPM) using graphical languages like BPMN or UML Activity Diagrams. Sev-

eral researchers have presented validation methologies for such BPMs. In order

to use these veriﬁcation techniques for BPMs written in graphical languages, the

models must be translated into the input language of a model checker or simu-

lation tool. By analyzing 285 BPMs (modelled as Event driven Process Chains

(EPC)), we found that checking restrictions for ”good modeling style” before

starting the translation process has three positive effects: It can make the transla-

tion algorithm much easier, can improve the quality of the BPM by substituting

”bad constructs” automatically and can help to identify erroneous models.

1 Introduction and Related Work

The correctness of a BPM is critical for the automation of business processes. It should

be possible to eliminate errors in a BPM at speciﬁcation time. Simulation and model

checking are two possible techniques that can be used to identify errors. In order to

apply these techniques, it is necessary to translate the BPM into the input language of a

model checker or simulation tool.

Several authors have published algorithms for translating high-level descriptions of

BPMs into something that can be understood by model-checkers or simulation tools

(usually Petri nets or ﬁnite-state automata).

For example, the Petri-net based tool Woﬂan[1] can interface with several workﬂow

management systems and check important properties of workﬂow models. Matousek[2]

translates business process models deﬁned in the XPDL language into the input lan-

guage of the SPIN model checker. UML activity diagrams are analyzed by Eshuis[3]

who uses the model checker NuSMV to verify properties and by Barjis et al.[4] who

transform them into a simulation model. Van Dongen et al. [5,6] use reduction rules

and Petri-Net analysis for verifying event driven process chain-models. (Note that this

list of papers on formal veriﬁcation of BPM is by far not complete.)

All these authors use algorithms for translating BPMs into Petri nets or ﬁnite-state

automata. These algorithms are intended to translate every BPM that is syntactically

correct. In contrast to this, we suggest to check restrictions for ”good modeling style”

before starting the translation and disallow models which failed the tests.

⋆

The Chair of Applied Telematics / e-Business is endowed by Deutsche Telekom AG

Gruhn V. and Laue R. (2006).

How Style Checking Can Improve Business Process Models.

In Proceedings of the 4th International Workshop on Modelling, Simulation, Veriﬁcation and Validation of Enterprise Information Systems, pages 47-56

DOI: 10.5220/0002474200470056

 SciTePress

In the following chapters, we will introduce a set of style rules and see that the

models which follow them are not just easier to understand, the suggested approach can

also help to identify common errors in the model.

In Sect. 2, we brieﬂy introduce the modeling language EPC that is used in this

paper. Semantical problems that arise from the so-called non-locality of OR-joins are

discussed in Sect. 2.2. In Sect. 3, we formulate style rules. There are rules for checking

good modeling style and also transformation rules for correcting common errors au-

tomatically, as discussed in Sect. 4. Sect. 5 gives some quantitative information about

how well our approach works with ”real-life models” we have collected from several

sources.

2 Event Driven Process Chains

2.1 Informal Semantics

Event driven Process Chains (EPC) are a popular technique for business process mod-

eling. Unfortunately, their initial authors did not deﬁne their precise semantics. Instead,

the informal semantics is given roughly as follows:

EPCs consist of three kinds of elements: functions (activities which need to be ex-

ecuted, depicted as rounded boxes), events (pre- and postconditions before / after a

function is executed, depicted as hexagons) and connectors (which can split or join the

ﬂow of control between the elements). Arcs between these elements represent the con-

trol ﬂow. Each EPC has one or more start events which carry a token (called process

folder) when the EPC becomes enabled and ”starts to run”. These tokens are propagated

through an EPC. Events and functions have at most one incoming and at most one out-

going arc, and the tokens are simply propagated from the incoming arc to the outgoing

arc.

Connectors are used to model parallel and alternative executions. There are six types

of connectors:

AND-connectors (depicted as

∧

) are used to model parallel execution. The and-

split connector propagates a token from its incoming arc to all its outgoing arcs. The

corresponding AND-join connector waits until a token has arrived on all of its incoming

arc before sending a token to the outgoing arc.

XOR-connectors (depicted as ×) can be used to model alternative execution:

A XOR-split has multiple outgoing arcs, but an incoming token will be propagated to

exactly one of them. The corresponding XOR-join waits for an incoming token on one

of its incoming arcs and propagates it to the outgoing arc.

Finally, OR-connectors (depicted as ∨) are used to model parallel execution of

one or more ﬂows. An OR-split propagates an incoming token to one or more of its

outgoing arcs. The corresponding OR-join waits until a token arrives on each of those

incoming arcs that can deliver a token and propagates it to the outgoing arc.

Of course, the above informal description is insufﬁcient and imprecise. However,

the informal description is sufﬁcient to interpret the meaning of the majority of EPC

diagrams.

check

references

read CV

references

checked

CV read

read

publications

read

Fig.1. Example EPC with OR-join.

There are several proposals for a formalization of the semantics of EPCs: [7] gives

a mapping from EPCs without OR-connectors onto Petri nets. [8] translates EPCs for

which certain well-formedness rules must hold onto Petri nets as well. Other papers on

deﬁning formal semantics include [9], [10] and [5].

2.2 Problems with OR-Joins

While the informal semantics discussed in 2.1 lead to a straightforward mapping of

functions, events, split connectors and XOR- and AND-join connectors to Petri nets or

other semantically well-founded models[7], there are serious problems with OR-join

connectors.

The easiest (and most common) usage for this connector is depicted in Fig. 1 which

shows a part of the process of recruiting and selecting academic staff. One, two or all

branches after the OR-split may be processed (by sending tokens). The corresponding

OR-join must wait until all tokens have arrived.

However, the decision whether more tokens can arrive on one of the incoming arcs

cannot be made locally at the OR-join. As the OR-split can send tokens to one, two

or all three outgoing arcs it is not even known whether the OR-join has to wait for

one, two or three incoming tokens. As the ”ﬁring condition” cannot be checked locally

at the OR-join, the semantics of this connector is called non-local. This non-locality

leads to serious problems when the formal semantics of the OR-join has to be deﬁned.

A detailed discussion of these problems is beyond the scope of this paper. We refer the

reader who is interested in this topic to [7,8, 11,12, 9,13]. The non-locality of OR-joins

can even raise problems to the effect that it is impossible to deﬁne a formal semantics

of EPCs that is fully compliant with the informal semantics. [14] gives a nasty example

(called the vicious circle), an EPC with two OR-joins in a feedback loop, each of them

waits for the other to complete ﬁrst. For this EPC, it is not possible to deﬁne a formal

semantics in a satisfying way.

Some authors, for example Kindler[14, 9, 13], interpret the meaning of an XOR-join with non-

local semantics as well. We follow the approach suggested by van der Aalst[7] instead and

assume that an XOR-join has local semantics and forwards every token that arrives.

From a theoretical point of view, these problems have been solved: Kindler[9] uses

techniques from ﬁxed point theory in order to deﬁne a semantics for EPCs (taking into

account that there are EPCs for which no suitable semantics exist.[14]). [12] and [13]

use backward marking and state space exploration techniques for calculating the en-

abledness of an OR-join. Both approaches calculate the semantics of moderately sized

models in a reasonable time. They aim to ﬁnd the semantics for every EPC where a

suitable semantics exists. Obviously this is the best possible solution from a theoretical

point of view. We argue, however, that in practice, it is not really desirable to compute

the semantics of every EPC model. If a BPM is modelled in a hard-to-read style, it is

very unlikely that domain experts who use this model as a basis for communication will

ﬁnd it useful.

For this reason, we asked for which kind of models it is difﬁcult to deﬁne the seman-

tics of the OR-join. As we will show in section 3, the answer was that these problems

occur for such models that have been modeled in what we call ”bad modeling style”.

Unfortunately, such models are not uncommon. One reason for this is that EPC (and

other business process modeling languages as well) do not require proper nesting, i.e.

splits and joins does not have to occur pairwise. This is comparable with programming

languages that do not only allow structured loops (like repeat...until etc.) but

also arbitrary GOTO-jumps. Not without a reason, [15] writes that ”the current unstruc-

tured style of business process modeling, which we can call spaghetti business process

modeling, leads to similar problems as spaghetti coding”.

Motivated by these observations, we wondered whether it would be possible to ﬁnd

a small number of rules for ”good modeling style” that...

1. do not ”forbid” existing EPCs for which domain experts would agree on their cor-

rectness and agree on their semantics.

2. do not seem to be ”artiﬁcal” or ”surprising”. (In contrast, good modelers should

already follow these rules intuitively.)

3. can easily be checked.

4. and (as a result of their ”structuredness”) ensure that models that follow the rules

can be translated into Petri-nets using an easy-to-implement algorithm (in particular

this means that these models have a well-deﬁned semantics).

The next section describes a set of rules meeting these requirements.

3 Style Rules

By analyzing EPCs from several sources (see section 5), we identiﬁed a set of ”style

rules” for OR-constructs. OR-constructs that follow these rules can be translated into

formally founded languages (like Petri nets), and our rules do not unnecessarily reject

too many EPCs as being not well-formed.

These style rules can be summarized in the following recursive deﬁnition for well-

structured OR-constructs. (In this deﬁnition, we abstracted away from functions and

events in the EPC, because the critical part is in the connectors):

Deﬁnition 1 (well-structured OR-constructs):

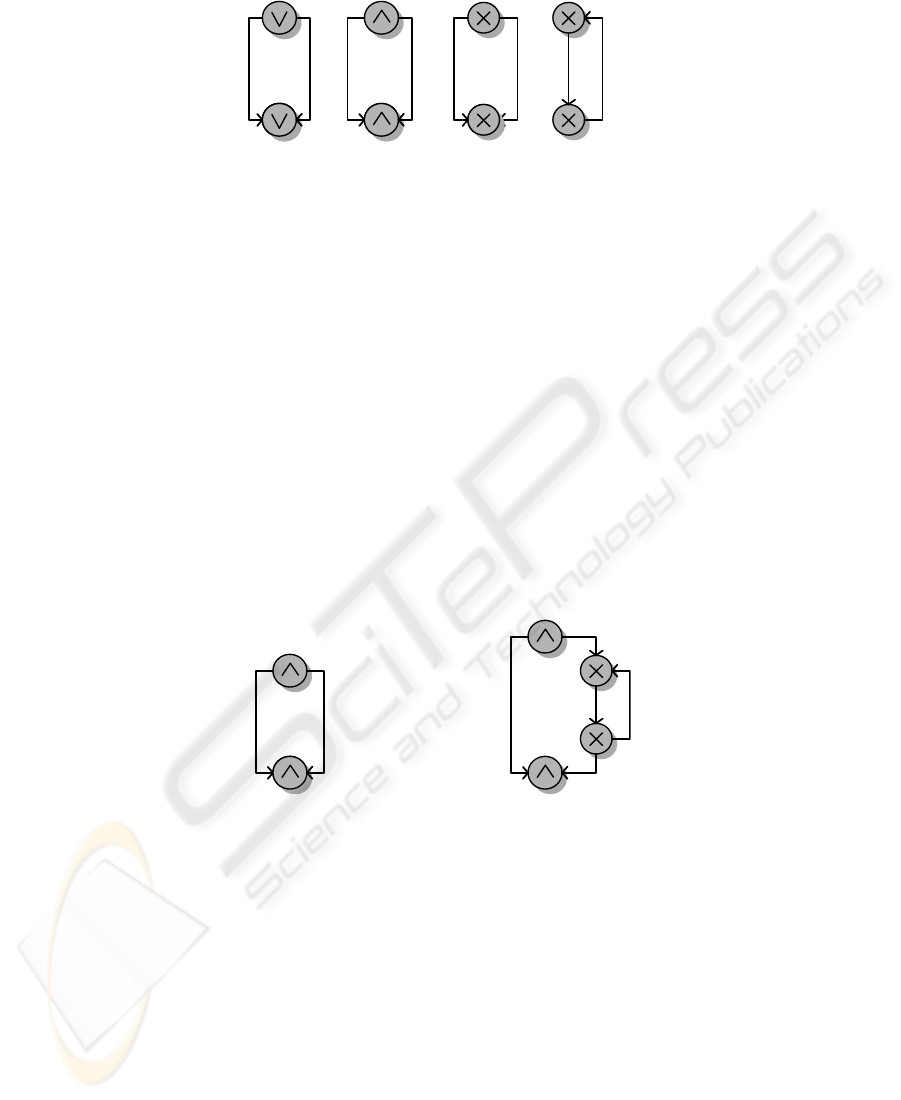
OR-construct AND-construct

(parallel flow)

XOR-construct

(alternative threads)

Iteration

a) b) c) d)

Fig.2. Workﬂow Constructs.

1. The workﬂow constructs shown in Fig. 2 are well-structured. While Fig. 2 a)-c)

shows only connectors with exactly 2 outgoing/incoming arcs, it is also allowed

that there are more than 2 arcs between the split connector and the join connector.

2. If a well-formed construct is ”inserted into an arc” of a well-structured construct

(see Fig. 3), the resulting construct is well-structured.

3. If an additional split is ”inserted into an arc” of a well-structured construct (see

Fig. 4, but note that the split does not have to be a XOR-split), the resulting con-

struct is well-structured.

4. If an arc of a well-structured construct is replaced by an event (to model termina-

tion of the ﬂow of control at this point, see Fig. 5), the resulting construct is well-

structured if the graph made by the arcs, functions and events is still a connected

graph.

a well-structured

construct:

Inserting another

well-structured construct

into one of its arcs

results in a well-

structured construct again:

Fig.3. Deﬁnition, part 2.

Roughly speaking, rules 1 and 2 make sure that each join-node corresponds to a

split-node. Rule 3 allows to ”jump out of a split-join construct”, but it is not allowed

to ”jump into a split-join construct”. Please note that it follows from the deﬁnition that

every join node has a corresponding split node of the same type, in particular every

OR-join must have a preceeding OR-split.

It is important to mention that the well-structuredness criterion must hold for every

construct between an OR-split and the corresponding OR-join, but not for the complete

EPC. For a given EPC, the validity of the above rules can be checked statically (i.e. no

simulation is needed).

jumped out of the

OR-construct

Fig.4. Deﬁnition, part 3.

STOP

Fig.5. Deﬁnition, part 4.

4 Correcting Common Errors Automatically

If a model fails the test of the style rules, often we can use the results of its analysis in

order to ﬁx it automatically. In our analysis of existing EPCs, we found a surprisingly

large number of models with common errors that can (and should) be improved auto-

matically based on the results of a static analysis. Fig. 6 shows these common errors

and their correction.

is corrected to:

b) c)

something

happens

is corrected to:

something

happens

is corrected to: is corrected to:

Fig.6. Common errors and their corrections.

In particular, we found that often modelers used OR-joins when a XOR-join or an

AND-join should be used. (See Fig. 6a)-c), where we have omitted functions and events,

because the error lies in the use of connectors only). Another common error was to use

OR-split/joins instead of XOR-constructs in order to model optional execution (Fig. 6

d)).

While the ”bad” constructs would be allowed according to the informal semantics,

they should be changed into models with an AND / XOR-join anyway. Note that these

corrections can change a construct that is not well-structured into a well-structured one

without changing its (yet informal) semantics. However, even if the semantics of the

model remains the same, the corrected one is more explicit and less likely to become

the source of misunderstandings and wrongful implementation.

Static analysis can also detect other errors that cannot be automatically ﬁxed. While

in this paper, we restrict our focus to errors that are related to OR-joins, we note that

similar style rules can be deﬁned for ﬁnding other classes of errors (for example con-

structs that start with an XOR-split but end with an AND-join which will result in a

deadlock).

5 Case Study

We have collected 285 EPCs from different sources (23 Masters thesises, 2 term papers,

4 PhD thesises, 5 textbooks, 30 scientiﬁc papers, lecture notes from a university course,

the SAP reference model and one of our own projects – the full list of sources can be

found on the web[16]). We tolerated EPCs with small syntactical errors, but 9 graphics

called an EPC in our sources had such signiﬁcant syntactical problems that we would

not regard them as being an EPC, we ignored them in the further analysis.

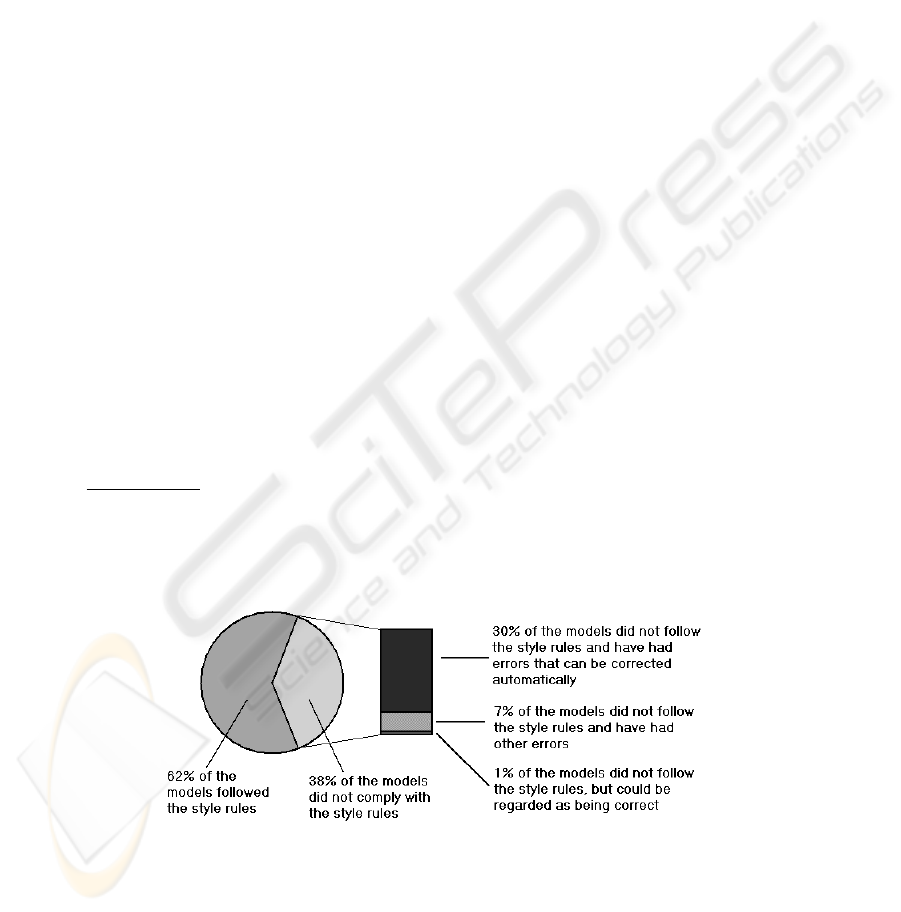
For the 276 remaining EPCs, we found that:

– 190 EPCs did not use OR-joins at all.

– The remaining 86 EPCs with OR-joins contained 151 OR-join connectors. 94 of

these connectors were either used in the trivial way (with a corresponding OR-split

and without any other connectors between the OR-split and the OR-join) or in a

well-structured way according Def. 1.

The most interesting result was the analysis of the remaining 57 OR-joins from not

well-structured constructs: 45 of them fell into one of the cases depicted in Fig. 6, i.e.

they should be replaced by another join node. For 10 other not well-structured models

with OR-joins, a closer inspection revealed that the model was faulty

, and the error

cannot be corrected automatically. This means that syntactically correct models that do

not pass our modeling style rules are most likely erroneous, and applying the style rules

can help to identify the errors almost immediately when the model has been drawn.

”Faulty” means here that either the model has structural defects like deadlocks or it has an

error in the business logic. In the latter case, the problem can only be identiﬁed manually,

because understanding the business process is necessary.

Fig.7. Results of the case study.

There were only 2 EPCs which could be regarded as being correct (i.e. the busi-

ness process would come to the desired result), but failed to comply with the well-

structuredness rules. However, these EPCs were also modelled in a unsatisfactory way,

in particular the soundness property as deﬁned in [17] was violated for these models.

Both models would proﬁt from a re-design.

Fig. 7 shows the results of our case study in a diagram.

6 Conclusion

From the above ﬁgures we conclude that almost all correct EPCs we have collected

followed the style rules. Moreover, if the analysis found that an EPC did not comply

with the style rules, in the vast majority of cases, this meant that in fact this model was

erroneous. Interestingly, the most of these errors could be corrected automatically as

the result of the static analysis.

We would like to stress that the fact that there were only 2 models that were correct

but failed the style check anyway is a result of our approach: We studied existing models

from various sources before formulating the style rules. For this reasons, the coverage of

our rules for well-structuredness is much better than in existing approaches, in particular

[8]. The problem with the restrictions posed on EPCs in [8] is that they exclude too

much existing EPCs from being regarded as well-formed. Too many models that are

well-modelled and can be used successfully in practice would be regarded as being

invalid. It seems to us that the well-formedness restrictions in [8] have been introduced

to ﬁt the theorists’ requirements for deﬁning an elegant algorithm for translating the

EPC into a Petri net, while they do not ﬁt the desires of those persons who actually use

EPC diagrams.

While our style rules are less restrictive than the ones published in [8], we can still

use the idea from [8] to translate EPC models that follow the style rules into a Boolean

net, a Petri net variant (or formally spoken: to deﬁne the semantics of the EPC). The

translation into a Boolean net is a generalization from the algorithm published in [8],

details can be found in [18].

We found that requiring and checking additional restrictions for ”good modeling”

as described in Sect. 3 has three positive effects:

1. The algorithm for the translation of the model into another (formally founded)

model that can be used in model-checkers or simulation tools becomes easier (com-

pared with algorithms like the ones from [19] or [13]).

2. The model can be improved automatically by correcting common errors (see Sect.

4).

3. Failing the style checks most likely means that the model is erroneous. This fact

helps us to detect errors immediately after the model has been drawn (and correct

them manually).

The usage of style rules for detecting possible errors in a BPM is somewhat heuris-

tic compared with other formal methods. However, this heuristic approach allows us

to identify problems that are not detected by other methods. In particular, this was the

case for the models that did not comply with the style rules but could not be ﬁxed auto-

matically. Most of them had an error in the business logic. An example in an EPC from

one of our own projects was an electric meter that was modelled as being working and

being out of order at the same time. Finding such ﬂaws requires the understanding the

underlying business process. Existing tools that check technical properties of a model

(like absence of deadlocks etc.) are unable to ﬁnd such errors. While human action is

required to ﬁnd the errors in the business logic, checking the style rules can guide us

which models should be inspected manually because they most likely contain an error.

We emphasize that the proposed approach of applying additional well-formedness

checks to business process models is not restricted to EPCs. For example, some ideas

from Sect. 3 can be directly applied to YAWL[20] models. Other languages will re-

quire other style checking rules. For example, the syntax for UML Activity Diagrams

allows syntactically correct but absolutely useless constructions[21]. Performing a style

check on such UML diagrams before using them will help to detect errors and sources

for misunderstandings in an early stage of a project. Such style checks can be inte-

grated into a BPM editor and used in a similar way as style checkers for software

like Splint (www.splint.org), JLint (jlint.sourceforge.net) or FindBugs

(findbugs.sourceforge.net) which are known for enhancing the code quality

of software.

References

1. Aalst, W.: Woﬂan: a Petri-net-based workﬂow analyzer. Syst. Anal. Model. Simul. 35 (1999)

345–357

2. Matousek, P.: Veriﬁcation of Business Process Models. PhD thesis (2003)

3. Eshuis, R.: Semantics and Veriﬁcation of UML Activity Diagrams for Workﬂow Modelling.

PhD thesis, University of Twente, Enschede (2002)

4. Barjis, J., Shishkov, B., Dietz, J.L.: Validation of business components via simulation. In:

proceedings of the 4th International Eurosim 2001 Congress. (2001)

5. van Dongen, B.F., Aalst, W., Verbeek, H.M.W.: Veriﬁcation of EPCs: Using reduction rules

and Petri nets. In: CAiSE. (2005) 372–386

6. van Dongen, B.F., Jansen-Vullers, M.H.: EPC veriﬁcation in the ARIS for MySAP refer-

ence model database. In: BETA Working Paper Series, WP 142, Eindhoven University of

Technology, Eindhoven. (2005)

7. Aalst, W.: Formalization and veriﬁcation of event-driven process chains. Information &

Software Technology 41 (1999) 639–650

8. Langner, P., Schneider, C., Wehler, J.: Relating event-driven process chains to boolean petri

nets. Report (1997)

9. Kindler, E.: On the Semantics of EPCs: A Framework for Resolving the Vicious Circle. In:

Business Process Management. (2004) 82–97

10. Dehnert, J., Aalst, W.: Bridging The Gap Between Business Models And Workﬂow Speciﬁ-

cations. Int. J. Cooperative Inf. Syst. 13 (2004) 289–332

11. Rittgen, P.: Quo vadis EPK in ARIS? Wirtschaftsinformatik 42 (2000) 27–35

12. Wynn, M.T., Edmond, D., Aalst, W., ter Hofstede, A.H.M.: Achieving a General, Formal

and Decidable Approach to the OR-Join in Workﬂow Using Reset Nets. In: ICATPN. (2005)

423–443

13. Cuntz, N., Freiheit, J., Kindler, E.: On the Semantics of EPCs: Faster calculation for EPCs

with small state spaces. In: EPK 2005, Gesch

aftsprozessmanagement mit Ereignisges-

teuerten Prozessketten. (2005) 7–23

14. Aalst, W., Desel, J., Kindler, E.: On the semantics of EPCs: A vicious circle. In: EPK 2004,

Gesch

aftsprozessmanagement mit Ereignisgesteuerten Prozessketten. (2002) 71–79

15. Holl, A., Valentin, G.: Structured business process modeling (SBPM). In: Information Sys-

tems Research in Scandinavia (IRIS 27) (CD-ROM). (2004)

16. Laue, R.: ebus.informatik.uni-leipzig.de/∼laue (2005)

17. Aalst, W.: The Application of Petri Nets to Workﬂow Management. The Journal of Circuits,

Systems and Computers 8 (1998) 21–66

18. Gruhn, V., Laue, R.: Einfache EPK-Semantik durch praxistaugliche Stilregeln. In: EPK

2005, Gesch

aftsprozessmanagement mit Ereignisgesteuerten Prozessketten. (2005) 176–189

19. Cuntz, N., Kindler, E.: On the semantics of EPCs: Efﬁcient calculation and simulation. In:

EPK 2004: Gesch

aftsprozessmanagement mit Ereignisgesteuerten Prozessketten, Proceed-

ings. (2004) 7–26

20. Aalst, W., Hofstede, A.: YAWL: Yet another workﬂow language. Technical Report FIT-TR-

2002-06, Queensland University of Technology, Brisbane (2002)

21. St

orrle, H.: Semantics of UML 2.0 Activities. In: Symposium on Visual Languages - Human

Centric Computing (VL/HCC’04, Proceedings), IEEE (2004) 235–242