
An N-gram Based Distributional Test for
Authorship Identification
Kostas Fragos
1
and Christos Skourlas
2
1
Department Of Computer Engineering, NTUA,
Iroon Polytexneiou 9, 15780 Athens GREECE
2
Department Of Computer Science, TEIA,
Ag. Spyridonos 12210 Athens GREECE
Abstract. In this paper, a novel method for the authorship identification
problem is presented. Based on character level text segmentation we study the
disputed text’s N-grams distributions within the authors’ text collections. The
distribution that behaves most abnormally is identified using the Kolmogorov -
Smirnov test and the corresponding Author is selected as the correct one. Our
method is evaluated using the test sets of the 2004 ALLC/ACH Ad-hoc
Authorship Attribution Competition and its performance is comparable with the
best performances of the participants in the competition. The main advantage of
our method is that it is a simple, not parametric way for authorship attribution
without the necessity of building authors’ profiles from training data. Moreover,
the method is language independent and does not require segmentation for
languages such as Chinese or Thai. There is also no need for any text pre-
processing or higher level processing, avoiding thus the use of taggers, parsers,
feature selection strategies, or the use of other language dependent NLP tools.
1 Introduction
A variety of methods (and programs) have been proposed in the literature for the
authorship attribution problem. Programs based on statistical techniques were
effective in discriminating authors. Statistical methods make the assumption that the
text of an author is characterized by a probability distribution. A number of statistical
tests have been developed checking for significant variances of various distributional
features [2], [10], [12]. Naïve Bayesian probabilistic classifiers make the “naïve”
assumption that the occurrence of a word is conditionally independent of all other
words if the category is known. McCallum and Nigam [5] have applied a classifier for
text categorization. They made the above mentioned assumption and used the joint
probability of words and text categories to estimate the probability of categories.
Neural networks were used to model the style of an author using the frequency of five
function words, normalized to zero mean and unit variance [4]. Multi-layer
perceptions were used by Tweedy [11] to attribute authorship to the disputed
Federalist papers. The normalized frequency of eleven common function words was
used as input to the neural network. The k-nearest neighbour classification classifies a
Fragos K. and Skourlas C. (2006).
An N-gram Based Distributional Test for Authorship Identification.
In Proceedings of the 3rd International Workshop on Natural Language Understanding and Cognitive Science, pages 139-148
DOI: 10.5220/0002474701390148
Copyright
c
SciTePress

new document finding the k nearest neighbours among the training documents. The
resulting classification is a kind of majority vote of the categories of these neighbours
[4]. Support vector machines try to find a model that minimizes the true error (the
probability to make a classification error) and are based on the structural risk
minimization principle [1]. Machine learning techniques and shallow parsing have
been used in a methodology for authorship attribution by Luyckx and Daelemans [7].
All the above methods, except the statistical tests, are called semi-parametric models
for classification, as they model the underlying distribution with a potentially infinite
number of parameters selected in such a way that the prediction becomes optimal.
The above authorship attribution systems have several disadvantages. First of all,
these systems invariably perform their analysis at the word level. Although word level
analysis seems to be intuitive, it ignores various morphological features which can be
very important to the identification problem. Therefore, the systems are language
dependent and techniques that apply for one language usually could not be applicable
for other languages. Emphasis must also be given to the difficulty of word
segmentation in many Asian languages. These systems, also, usually involve a
feature elimination process to reduce dimensionality space by setting thresholds to
eliminate uninformative features [8]. This fact could be extremely subtle, because
although rare features contribute less information than common features, they can still
have an important cumulative effect [9].
To avoid these undesirable situations, many researchers have proposed different
approaches, which work in a character level segmentation [13], [14]. Fuchun et al.
[14], have shown that the state of the art performance in authorship attribution can be
achieved by building N-gram language models of the text produced by an author.
These models play the role of author profiles. The standard perplexity measure is then
used as the similarity measure between two profiles. Although these methods are
language independent and do not require any text pre-processing, they still rely on a
training phase during which the system has to build the author’s profile using a set of
optimal N-grams. This may be computationally intensive and costly, especially when
larger n-grams are used.
In this paper, we apply an alternative non parametric approach to solve the authorship
identification problem using N-grams at a character level segmentation (N-
consecutive characters). We compare simple N-grams distributions with the normal
distribution avoiding thus the extra computational burden of building authors’
profiles. For a text with unknown authorship, for all the possible N-grams in the text
we calculate their distributions in each one of the authors’ collection writings. These
distributions are then compared to the normal distribution using the Kolmogorov -
Smirnov test. The author, whose the derived distribution is behaved more abnormally
is selected as the correct answer for the authorship identification problem. We expect
the n-grams of the disputed text to be more biased against the correct and should be
distributed more abnormally in the correct author’s collection writing, than the other
authors’ writings. Such an abnormality is caught by the Kolmogorov-Smirnov test.
Our method is language independent and does not require segmentation for languages
such as Chinese or Thai. There is no need for any text pre-processing or higher level
processing, avoiding thus the use of taggers, parsers, feature selection strategies, or
other language dependent NLP tools. Our method is also simple, not parametric
without the necessity of building authors’ profiles from training data.
140

The use of N-grams, in Natural Language Processing tasks, is presented in section 2.
In section 3 the Kolmogorov - Smirnov test is discussed. The proposed algorithm and
an example of using it are presented in section 4 and 5. In section 6 some
experimental results are given. We conclude this paper with a discussion of the
proposed algorithm.
2 The Use of N-grams
An N-gram is a sequence of length N. We could be looking at sequences of N
characters, N words or tokens within texts, but the idea is much more general. The use
of N-grams is a simple yet effective traditional tool of studying important aspects in
Natural Language Processing as well as in many other applications, such as speech
recognition, biology, etc. Character level N-gram models have been successfully used
in text compression [13], text mining [16] and text classification problems [17].
An N-gram is like a moving window over a text, where N is the number of text items
(character, words, etc) in the window. For two consecutive items the N-gram is called
bigram, for three consecutive items trigram, for four consecutive items quadrigram,
and so on.
As it was aforementioned, in this work we use N-grams at a character level
segmentation. If our text contains M characters, totally, then the number of possible
N-grams derived from the text is:
1
+
−= NMNgramsPossible
(1)
For example, for the text passage “author name” consisting of M=11 characters we
have the following 7 5-grams (N=5):
“autho”, “uthor”, “thor ”, “hor n”, “or na”, “r nam”, “ name”.
Just counting the appearances of all the possible N-grams of the disputed text within
the author’s known text collection we compute the empirical N-gram distribution for
this particular author. These N-gram distributions are then compared with the normal
distribution to decide for the correct author. How this is done is described in the
following section.
3 Testing for Normality
In statistics, the Kolmogorov-Smirnov test (KS-test) is used to determine whether
there is a difference between two underlying probability distributions based on finite
samples or whether an underlying probability distribution differs from a hypothesized
one [3]. The main use of the test is for testing goodness of fit with the normal and
uniform distributions. It is a more powerful alternative to chi-square goodness-of-fit
tests when its assumptions are met.
The KS-test is an ideal test for capturing abnormalities within a data sample. That is
why we use this test to study the distributions of N-grams within the authors’ text
writings. Moreover, the KS-test has the advantage of making no assumption about the
distribution of the data sample (the disputed text in our authorship identification
141

problem). Technically speaking it is non-parametric and distribution free, whereas t-
test for example makes the strong assumption that the data is distributed normally
which is no true in the case of text N-grams.
The essence of the test is very simple. The application of the KS-test comprises the
following basic steps:
• Calculation of the cumulative frequency distribution function (normalized by the
sample size) of the observations in the data sample as a function of the data classes.
• Calculation of the cumulative frequency for a true distribution, most commonly the
normal distribution.
• Finding of the greatest discrepancy between the observed and expected cumulative
frequencies, which is called the "D-statistic". This value of discrepancy is then
compared against the "critical D-statistic" for that sample size. If the calculated D-
statistic is greater than the critical one, then we reject the hypothesis (null hypothesis)
that the distribution is of the expected form.
The KS-test is based on the empirical distribution function (ECDF). Given N order
data points y
1
,y
2
,..,y
N
the ECDF is defined as
NinF
N
/)(= (2)
where n(i) is the number of points less than y
i
and the y
i
’s are ordered from smallest to
largest value. This is a step function that increases by 1/N at the value of each ordered
data point.
The D-statistic is given by:
)max( FFD
N
−= (3)
Where F is the cumulative frequency for the hypothesized distribution (usually the
normal distribution).
The computed D is compared to a table of critical values of D in the Kolmogorov-
Smirnov One-Sample Test, for a given sample size [3].
The KS-test is only applied on continuous hypothesized normal distributions, such as
normal, weibull, etc. For the normal distribution, the expected sample mean and
sample standard deviation must be specified in advance.
4 The Proposed Method for Authorship Identification
Our approach is based on byte level N-grams. It calculates the empirical distribution
from the sample and compares it with the normal distribution for capturing
abnormalities. For a piece of text whose authorship is unknown (disputed text), we
form all the possible N-grams (N consecutive characters) the number of which is
given by equation (1). For each N-gram we count the frequency of appearance within
the authors’ text writings, forming thus an empirical distribution of the N-grams for
each author collection. We expect that the distribution which corresponds to the
correct author should behave differently in comparison with the other authors’
distributions. To capture this differentiation we compare the distributions with the
normal distribution using the KS-test. The author whose distribution is behaved more
abnormally is selected as the correct author of the disputed text. To form the possible
N-grams we take into account all the printable characters in the disputed text,
included punctuation marks, numbers and generally every legal typographic character,
142

as we believe these represent the richness of the author’s vocabulary and help our
algorithm to deal with the whole linguistic device the author uses to produce his text.
The proposed algorithm is figured out below:
proc main
For a given N (e.g., for bigrams use N=2), form all the
possible N-grams in the disputed text.
Calculate the empirical distribution of these N-grams in
each one of the authors’ text writing collections.
Perform the Kolmogorov-Smirnov test for normality for
each one of the calculated distributions in the previous
step.
Choose as correct author of the disputed text, the
author whose corresponding distribution has the lower D-
statistic value from the test.
endproc
5 An Example and the Related Discussion
To clarify our method let us focus on a specific example and discuss how our
algorithm is working.
We used real data from the contest materials of the 2004 “Ad-hoc Authorship
Attribution Competition” [6], (see subsection 6.1 for a description of this test sets).
For disputed text we used the file Atrain01-1. The letter A in the file name denotes a
text document from the problem A of the competition, the substring train denotes that
this text could be used for the training of the algorithm, the 01 is the number of
author who wrote the text and the final digit is the number of training sample for this
particular author. For authors’ collection text writings we used the files Atrain01-2
and Atrain01-3 for Author 1, Atrain02-2 and Atrain02-3 for Author 2 and finally the
files Atrain03-1 and Atrain03-2 for Author 3.
The disputed text Atrain01-1 has a file size of about 3 Kbytes in disk. The Authors’
collection writings have file size of about 9, 9 and 11 Kbytes for Author 1, Author 2
and Author 3 respectively.
The number of all possible bigrams in the disputed text is 2,477 included all the
characters in the text. Counting the occurrences of these bigrams within an author’s
text writing we form the empirical bigram distribution for this particular author.
In the figure 1 below, the histograms of occurrences of these bigrams within each
Authors’ text collection writing are shown.
143
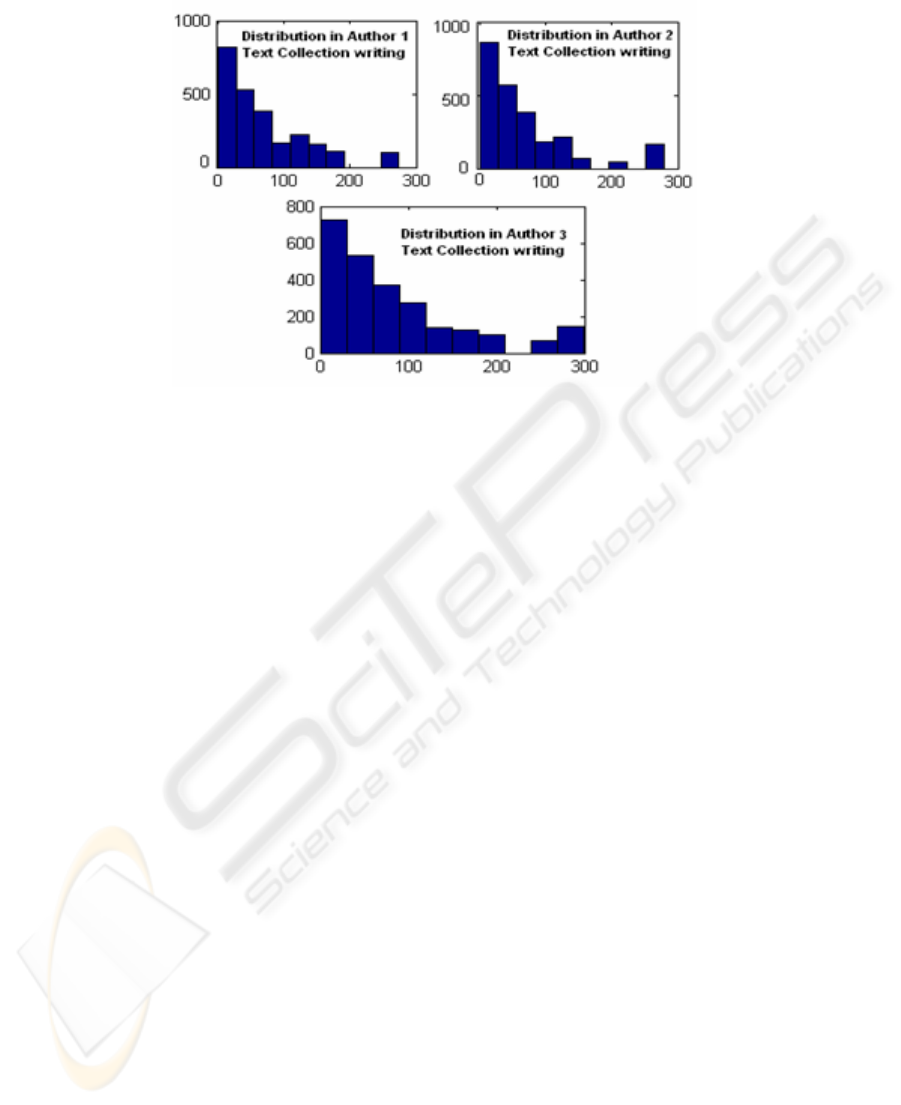
Fig. 1. Histograms of occurrences of the 2,477 bigrams of the disputed text in the three
Authors’ text writing collections (from the demonstration example of section 5).
For the three distributions we perform the KS-test for normality. The calculated D-
Statistic values are:
For the distribution in Author 1’s collection the value of D-Statistic is 0.14273, for the
distribution in Author 2’s collection is 0.16725 and finally for the distribution in
Author 3’s collection is 0.14979. The distribution with the smaller D-Statistic value
is the distribution in the Author 1’s text collection writing. Hence the correct Author
of the disputed text is the Author 1. This is true for our example data.
6 Evaluation
In this section we describe the experimental dataset used for this work as well as the
evaluation results of the proposed algorithm.
6.1 The Experimental Data
In July 2004, the ALLC/ACH conference hosted an “Ad-hoc Authorship Attribution
Competition” [6]. The main contribution of this competition was to provide a
standardized test corpus for authorship attribution. Contest materials included thirteen
problems, in a variety of lengths, styles, genres, and languages, mostly gathered from
the Web but including some materials specifically gathered to this purpose. The
participants tested their algorithms upon the materials and returned their attributions
to be graded and evaluated against the known correct answers. The specific problems
presented included the following:
• Problem A (English): Fixed-topic essays written by thirteen Duquesne students
during fall 2003.
144

• Problem B (English): Free-topic essays written by thirteen Duquesne students
during fall 2003.
• Problem C (English): Novels by 19th century American authors (Cooper, Crane,
Hawthorne, Irving, Twain, and ‘none-of-the-above’), truncated to 100,000 characters.
• Problem D (English) First act of plays by Elizabethan/ Jacobean playwrights
(Johnson, Marlowe, Shakespeare, and ‘none-of-the-above’).
• Problem E (English) Plays in their entirety by Elizabethan/Jacobean playwrights
(Johnson, Marlowe, Shakespeare, and ‘none-of-the above’).
• Problem F ([Middle] English) Letters, specifically extracts from the Paston letters
(by Margaret Paston, John Paston II, and John Paston III, and ‘none-of-the-above’ )
• Problem G (English) Novels, by Edgar Rice Burrows, divided into “early” (pre-
1914) novels, and “late” (post-1920).
• Problem H (English) Transcripts of unrestricted speech gathered during committee
meetings, taken from the Corpus of Spoken Professional American-English.
• Problem I (French) Novels by Hugo and Dumas (pere).
• Problem J (French) Training set identical to previous problem. Testing set is one
play by each, thus testing ability to deal with cross genre data.
• Problem K (Serbian-Slavonic) Short excerpts from The Lives of Kings and
Archbishops, attributed to Archbishop Danilo and two unnamed authors (A and B).
Data was originally received from Alexsandar Kostic.
• Problem L (Latin) Elegiac poems from classical Latin authors (Catullus, Ovid,
Propertius, and Tibullus).
• Problem M (Dutch) Fixed-topic essays written by Dutch college students, received
from Hans van Halteren.
In each of these thirteen problems the data is grouped into two categories: The
training data sample and the test data sample. The training data sample contains for
each of the Authors in the problem a small number of text documents (usually 4-8),
representative for this Author’s writing style. The test data sample contains a text
document for each Author. The test texts are given to the participants in the
competition anonymized, that is, they do not know the name of the correct Author
who wrote the text. The participants are asked to attribute the text to the correct
Author.
6.2 Performance
We decided to evaluate the proposed algorithm upon the training part of the
evaluation data. In each problem the training data has the same structure as in the
testing part. For each author, a suitable number of text documents are given which
describes this author’s text writing profile. From all the authors’ text documents we
selected the first document as the disputed text and the remaining documents as the
author’s text writing collection.
The Authors’ text writing collections were truncated to the smallest size of the text
collections to make the collections equally sized.
In all the experiments, before we apply KS-test for capturing abnormalities we
transformed the N-gram frequencies using the logarithmic transformation to make the
distributions more (nearly) normal.
145

The evaluation results for each one of the above problems are shown in the table 1 for
the cases of N=4 (qutrigrams) and N=5 (fivegrams).
Table 1. Precision of the proposed algorithm using N-gram distributions (for N=4,5). Problems
A to M of the 2004 ALLC/ACH Ad-hoc Authorship Attribution Competition.
Problem Performance
4-grams(N=4) 5-grams(N=5)
Problem A 7/13 (53.85%) 8/13 (61.54%)
Problem B 5/13 (38.46%) 5/13 (38.46%)
Problem C 3/5 (60%) 5/5 (100%)
Problem D 3/3 (100%) 3/3 (100%)
Problem E 3/3 (100%) 3/3 (100%)
Problem F 2/3 (66.67%) 2/3 (66.67%)
Problem G 1/2 (50%) 0/2 (0%)
Problem H 2/3 (66.67%) 2/3 (66.67%)
Problem I 1/2 (50%) 2/2 (100%)
Problem J 1/2 (50%) 2/2 (100%)
Problem K 2/3 (66.67%) 3/3 (100%)
Problem L 2/2 (100%) 1/2 (50%)
Problem M 4/8 (50%) 5/8 (62.5%)
Summary Results 850.377% 945.83%
To make a comparison with the participant systems of the 2004 ALLC/ACH
competition, we give in table 2 the total performance results attained by the systems
in the competition.
Table 2. Evaluation results of the 13 participants in the 2004 ALLC/ACH Ad-hoc Authorship
Attribution Competition.
Name Total result
1. Baronchelli 745.88%
2. Coburn 803.57%
3. Halteren 861.47%
4. Hoover1 738.18%
5. Hoover2
975.32%
6. Juola 850.58%
7. Keselj1
896.52%
8. Keselj2 612.97%
9.L. Amisano1 208.33%
10.LAmisano2 125.00%
11. Rudner 491.67%
12. Schler
917.95%
13. Stamatatos 755.17%
146

7 Conclusion and Further Work
In this work we presented a novel method for computer-assisted authorship
attribution. This method is working on a character level segmentation comparing the
distribution of all the possible N-grams of the disputed text with the normal
distribution. The Author whose distribution is behaved more abnormally is then
selected as the correct Author for the disputed text. The method does not require any
training for building Authors’ profiles. The Kolmogorov-Smornov test was selected to
be used as the goodness of fit test for testing the normality of the empirical
distributions because this test makes no assumption about the distribution of the
disputed text’s data.
An interesting direction for future work could be to use an alternative to the normal
distribution for testing the empirical distributions. We could estimate a distribution
from the Author’s text writing collection and then compare the estimated distribution
with the empirical distribution of the disputed text using the same test. This may
improve the performance of the proposed algorithm.
Acknowledgements
This work was co-funded by 75% from the E.U. and 25% from the Greek
Government under the framework of the Education and Initial Vocational Training
Program – Archimedes.
References
1. Derich, J., et al.: Authorship attribution with support vector machines. Applied Intelligence,
19(1-2): (2003) 109-123.
2. Goel, L. A.: Cumulative sum control charts. In S.Kotz and N. Johnson, editors,
Encyclopedia of Statistics, volume 2, Wiley (1982) 233-241.
3. Neal, D. K.: Goodness of Fit Tests for Normality, Mathematica Educ. Res. 5, 23-30.
Massey, F. J. Jr., 1951. The Kolmogorov-Smirnov test of goodness of fit, Journal of the
American Statistical Association, Vol. 46 (1996).
4. Lowe D. and Mattews R.: Shakespeare vs. Fletcher: A stylometric analysis by radial basis
functions, Computers and the Humanities, 29: (1995) 449-461.
5. McCallum and Nigam K.: A comparison of event models for naive Bayes text
classification. In AAA-98 Workshop on Learning for Text Categorization (1998).
6. Juola, P.: Ad-hoc authorship attribution competition. In Proc. of Joint International
Conference of the Association for Literary and Linguistic Computing and the Association
for Computers and the Humanities, Goteborg, Sweden ALLC/ACH (2004).
7. K. Luyckx and W. Daelemans: Shallow Text Analysis and Machine Learning for
Authorship Attribution. In: Proceedings of the Fifteenth Meeting of Computational
Linguistics in the Netherlands (2005).
8. Scott S. and Matwin S.: Feature engineering for text classification. In Proceedings ICML-
99, Florida (1992).
9. Aizawa A.: Linguistic techniques to improve the performance of automatic text
categorization. In Proceedings 6th NLP Pac. Rim Symp. NLPRS-01 (2001).
147

10. Thisted B. and Efron R.: Did Shakespeare write a newly discovered poem? Biometrika,
74:445-55 (1987).
11. Tweedie J. F., Singh S. and Holmes I. D.: Neural network applications in stylometry: The
Federalist papers. Computers and the Humanities, 30:1-10 (1996).
12. Valenza R. J.: Are the Thisted-Efron authorship tests valid? Computers and the
Humanities, 25:27-46 (1991).
13. Keselj V.: Perl package Text N-grams. http://www.cs.dal.ca/~vlado/srcperl/Ngrams or
http://search.cpan.org/author/VLADO/Text-Ngrams-0.03/Ngrams.pm, (2003).
14. Fuchun P., Schuurmans D., Keselj V. and Wang, S.: Automated authorship attribution with
character level language models. In Proceedings of the 10th Conference of the European
Chapter of the Association for Computational Linguistics, Budapest, Hungary, April 12-17
EACL (2003).
15. Bell, T. Cleary J. and Witten I.: Text Compression. Prentice Hall. (1990).
16. Mahoui M., Witten I., Bray Z. and Teahan W.: Text mining: A new frontier for lossless
compression. In Proceedings of the IEEE Data Compression Conference DCC (1999).
17. Cavnar W. and Trenkle, J.: N-gram-based text categorization. In Proceedings SDAIR-94
(1994).
148
