Prediction of Protein Tertiary Structure Class from

Synchrotron Radiation Circular Dichroism Spectra

Andreas Procopiou

, Nigel M. Allinson

, Gareth R. Jones

, David T. Clarke

Department of Electrical and Electronic Engineering, The University of Sheffield,

Mappin Street, Sheffield, UK

CCLRC Daresbury Laboratory, Warrington, UK,

Abstract. A new approach to predict the tertiary structure class of proteins from

synchrotron radiation circular dichroism (SRCD) spectra is presented. A

protein’s SRCD spectrum is first approximated using a Radial Basis Function

Network (RBFN) and the resulting set is used to train different varieties of

Support Vector Machine (SVM). The performance of three well known multi-

class SVM schemes are evaluated and a method presented that takes into

account the properties of spectra for each of the structure classes.

1 Introduction

Synchrotron radiation circular dichroism (SRCD) [1] spectroscopy provides a simple

and relatively fast experimental procedure for revealing the secondary structure of

proteins and their folding motifs. It can be exploited for almost any size of

macromolecule and can even assist in the determination of some elements of a

protein’s tertiary structure. Proteins are classified into five main structural groups

according to their domains: α, β, α + β, α/β and unordered or denatured proteins that

have little ordered structure [2]. The circular dichroism (CD) spectra of proteins

exhibit unique characteristics depending on these five classes [3]. The CD spectra of

α proteins exhibit strong double minima at 222 nm and 208 – 210 nm as well as a

stronger maximum at 192 – 194 nm. The β proteins produce spectra that usually have

a single negative and a single positive band; however the positions of these bands

vary and their intensities are much lower than those of α proteins. For α + β and α/ β

proteins, the intensities of spectra are more similar to the alpha helix structure since

usually it dominates over those of beta sheets. The CD spectra of other proteins have

a strong negative band between 198 – 200 nm.

The first attempt to relate CD spectra to the tertiary structure involved the visual

examination of the spectra together with several other criteria for determining the

class [4]. A mathematical technique of cluster analysis was proposed in [5], and was

able to identify α, α/β proteins but performed very poorly when tested on

polypeptides which were wholly α-helical or β-sheet, identifying them both as

belonging to the α/ β class.

Procopiou A., M. Allinson N., R. Jones G. and T. Clarke D. (2006).

Prediction of Protein Tertiary Structure Class from Synchrotron Radiation Circular Dichroism Spectra.

In 6th International Workshop on Pattern Recognition in Information Systems, pages 58-67

DOI: 10.5220/0002478200580067

 SciTePress

In this paper we use a Radial Basis Function Network (RBFN) and various Support

Vector Machines (SVM) to classify proteins into the five classes according to their

SRCD spectra. When an SRCD spectrum is presented to the system, the RBF network

provides a set of basis functions that are used as inputs to an SVM, which decides the

class of the test protein. The SVM was chosen as they have several attractive

characteristics as they are statistically-based models rather than loose analogies of

natural learning systems, and they have some theoretical guarantee of performance

[6]. They are designed for two-class problems as they seek to find a hyperplane in the

feature space that maximally separates the two target classes.

The remainder of the discussion is organized as follows – the task is placed in its

context by providing some background on the structural organization of proteins,

outlining both RBF networks and SVMs, and then details of the experimental

procedures. This is followed by a discussion of the results when different varieties of

SVM are used.

2 Protein Structure

All structural and functional properties of the proteins derive from the chemical

properties of their polypeptide chains. There are four levels of protein structural

organization: primary, secondary, tertiary and quaternary.

The primary structure of a protein is the sequence of amino acids from which it is

constructed [7]. The secondary structure refers to the arrangement of the amino acids

that are close together in a chain. There are three common secondary structures in

proteins, namely alpha helices, beta sheets and turns [2]. Those that cannot be

cataloged as one of these standard three classes are usually grouped into a category

called other. A beta sheet is constructed from beta strands form different regions of

the polypeptide chain; in contrast to an alpha helix, which is formed from one

continuous region. Thus beta sheets are composed of two or more straight chains that

are hydrogen-bonded side by side. If the amino termini are at the same end, the sheet

is termed parallel, and if the chains run in the opposite directions (amino termini at

opposite ends), the sheet is termed antiparallel. Turns are the third of the three main

secondary structures with approximately one-third of all residues in globular proteins

contained in turns that reverse the direction of the polypeptide chain.

Tertiary structure refers to the complete three-dimensional structure of the

polypeptide units of a given protein. Included in this description is the spatial

relationship of different secondary structures to one another within a polypeptide

chain and how these secondary structures themselves fold into the three-dimensional

form of the protein. For small globular proteins of 150 residues or fewer the folded

structure involves a spherical compact molecule composed of secondary structural

motifs with little irregular structure. For larger proteins the tertiary structure may be

organized around more than one structural unit, each of these called a domain.

However those interactions are fewer than the interactions of the secondary structural

elements within a domain [2].

Finally the highest level of proteins structural organization is the quaternary

structure. It results from the association of independent tertiary units through surface

interaction to form a functional protein.

The two main classification schemes that categorize proteins according to their

structure are the Structural Classification of Proteins (SCOP) [8] and the CATH [9].

The SCOP system currently shows 1028 unique folds although CATH shows 709. In

the SCOP proteins are classified into five main structural classes: α structures where

the core is build up mainly from alpha helices; β structure which comprise mainly

beta sheets; α+β structures, where proteins have alpha helices and beta sheets often in

separated domains, and α/β structures, where proteins have intermixed segments that

often alternate along the polypeptide chain. The fifth class refers to unordered or

denatured proteins that have little ordered structure. In the CATH the classes α+β and

α/β are combined to one class, the rest of them are the same.

3 Introduction to Employed Pattern Recognition Methods

3.1 Radial Basis Function Network

The Radial Basis Function Network is a widely used fast learning algorithm, first

introduced by Broomhead and Lowe [10]. RBF networks can perform both

classification and function approximation. For classification, the attraction of RBFs

can be explained by Cover’s theorem on the separability of patterns. This theorem

states that nonlinearly separable patterns can be separated linearly if the pattern is cast

nonlinearly into a higher dimensional space. Concerning function approximation,

theoretical results on multivariate approximation constitute the basic justifying

framework. In this paper, RBFs are only introduced as a technique for function

approximation.

The essential form of the RBF neural networks mapping is given by:

= w

(x)

i=1

∑

+ b

(1)

where w are the weight parameters and

is the basis function [11]. There are several

forms of basis function with the most common being the Gaussian:

(x) = e

−

x −

(2)

where x is the n-dimensional input vector with elements

and

is the vector

determining the centre of the basis function.

Training Radial Basis Function Network

Four parameters are adjusted during training. Namely, the number of basis functions

M, the width parameters,

, the centre locations,

and the weights, w

. The optimal

number of centers, M, for a given set is found by using a series of trial values and

computing the corresponding prediction error which is estimated using various model

selection criteria such as generalized cross validation (GCV)[12, 13]. The number

with the minimum prediction error is chosen as the optimal i.e. the estimated

prediction error is the smallest.

The location of the centers can be found in a variety of ways. The simplest is to

choose the centers as a subset of the data points. The choice can be random or linearly

spread along the data set. Unsupervised techniques can be used to cluster the input

vector and then using the centers of the clusters as the centers of the basis functions.

The most common algorithm used is the well-known K-means algorithm. The width

parameter is usually chosen to be the same for all basis functions and its value to be

some multiple of the average spacing between the basis functions. This ensures that

the basis functions are overlapping to some degree and hence give a relatively smooth

representation of the distribution of the training data.

Given the width and the centers of the basis functions, the weights

can be

calculated. As derived in [12] the weights are found using:

w = A

−1

(3)

where H is an N x M matrix such that

) , and is called the design

matrix.

−1

, the variance matrix, is given by A

−1

= H

H +Λ

⎛

⎝

⎜

⎞

⎠

⎟

−1

. The elements of

the matrix Λ are all zero except for the regularization parameters along its diagonal.

3.2 Support Vector Machines

Support Vector Machine is one kind of learning machines based on statistical learning

theory. It was firstly introduced by Vapnik [14]. This paper only considers the use of

SVMs for pattern classification, although they have also been applied to other areas

such as regression and novelty detection. The basic idea of applying an SVM to

pattern classification can be stated briefly as following: First, map the input vectors

into one feature space (possible at a higher dimension), either linearly or nonlinearly,

which is relevant with the selection of the kernel function. Then, within the feature

space from the first step, seek an optimized linear division, i.e., construct a

hyperplane that separates the two classes (this can be extended to multi-class). SVM

training always seeks a global optimized solution and avoids overfitting, so it has the

ability to deal with a large number of features.

For a two-class classification problem consider the data set x of N samples

< x

, y

>,...,< x

, y

> . Each sample is composed of a training example

of length

k, with elements

=< x

, x

,..., x

> , and target value y

∈{−1, 1} . The decision

function implemented by the SVM can be written as:

f (x) = s ign

i=1

∑

K(x

, x) + b

⎛

⎝

⎜

⎞

⎠

⎟

(4)

Where the coefficients

are the Lagrange multipliers and are obtained by solving

the following convex Quadratic Programming (QP) problem [6]:

Maximize

i=1

∑

−

j =1

∑

i=1

∑

K(x

, x

)

(5)

Subject to

0 ≤

≤ C

1=1

∑

= 0

(6)

The coefficients

are equal to zero for all the training samples, expect the support

vectors (i.e. the samples that lies on the hyperplane). In the above formulation the

regularization parameter, C, is a constant determining the trade-off between two

conflicting goals, maximizing of the margin and minimizing the misclassification

error.

The kernel,

K(x

, x

) , computes the inner product in feature space as a direct

operation upon the data samples in their original space [15]. If the feature-space is of

much higher dimension than the input space, this implicit calculation of the dot-

product removes the need to explicitly perform calculation in feature space.

Consequently, if an effective kernel is used, finding the separating hyperplane can be

done without any significant increase in computation time. Typical kernel functions

are:

K(x

, x

) = (x

⋅ x

)

(7)

K(x

, x

) = e

− x

−x

(8)

Equation (7) is the polynomial kernel function of degree d, which will revert to a

linear function when d is set to one. Equation (8) is a Gaussian kernel with a single

parameter σ.

For a given dataset, only the kernel function and the regularization parameter C are

selected to specify a SVM. The latter is varied through a wide range of values and the

optimal value is found using cross-validation. The choice of kernel and its parameters

is important since if they are poorly chosen the hypothesis modeling the data can be

oversimplify or too complex leading to poor generalization. The best way to make

the appropriate choice is using cross-validation since the choice is validated by

numerous independent tests. However a large data set is required for this method.

Various methods for estimating the kernel parameter, based on theoretical arguments

without the use of additional validation data have been proposed, with the most

economical approach is to use the leave-one-out cross validation procedure [6].

Multi-class SVM

SVM are inherently binary classifiers so techniques are needed to extend the method

to handle multiple classes. The goal of such techniques is to map the generalization of

the binary classifiers to a multi-class domain.

One vs. One Classifier

The One vs. One classifier system was proposed by Friedman [16] and has become

the most popular and successful multi-class SVM method. This classifier creates a

binary SVM for each combination of classes possible. Then for each unseen example,

each binary SVM assigns one vote to one of the two competitive classes and the

example is assigned to the class with the higher overall votes.

DAGSVM

DAGSVM stands for Directed Acyclic Graph SVM. This method was proposed by

Platt [17]. It employs exactly the same training phase as in “One vs. One” method

described above. However it characterizes itself in the classification phase by

constructing a rooted tree structure. Each node on the tree is a binary SVM for a pair

of classes. At the lowest level the number of leaves corresponds to the number of

classes. Every non-leaf node has two edges one that corresponds to not being the first

class and the other corresponds to not being the second class.

One Vs Rest Classifier

This method requires the building of many binary SVMs as the number of different

classes. Each attempts to construct a decision boundary separating one class from the

rest. Creating the models is accomplished by assigning the label “+1” to one class and

the label, “-1”, to all remaining classes.

The advantage of this method is that there are few SVMs involved, resulting in

much faster evaluation than the previous schemes. However, since all classes are

involved in each SVM, training of the SVMs can be time-consuming.

4 Method for Predicting the Protein Tertiary Structure Class

The reference set consisted from 28 proteins, as shown in the Table 1. According to

the SCOP system, eight of them belong to class α, five to class β, six to class α+β

five to class α/β and four to class “others”. Each CD spectrum has wavelength range

of 168 – 260 nm with values been recorded every 0.5 nm.

RBFs were used to approximate each spectrum as described above. The input data

were the wavelength values, which of course is the same for all spectra. The target

values were the intensity values for each of the spectra. The form of basis function

used was the Gaussian as it is the most commonly used function. Since the input data

are linearly spread from 168 to 260 at steps of 0.5, then there is no requirement to use

any algorithm to determine the location of the centers. Instead the centers are linearly

spread across the above range at constant steps depending on the number of centers.

The width parameter was chosen to be the same for all basis functions. Its value was

set to be equal to the spacing between the basis functions. Finally the optimal value

for the number of centers, M, had to be found. For this, the generalized cross

validation (GCV) was used. The GCV was calculated from three centers up to and

including 40 centers, keeping all other parameters the same. The graph of M against

the GCV value is shown in Fig 1.

Table 1. Protein refernce set.

Name Code Name Class

Chymotrypsin

CHYM

Cytochrome C CYTC

Elastase

ELAS

Haemoglobin HAEM

Lactate

Dehydrogenase

LADH

αβ

T4 lysozyme

LYSO

αβ

Myoglobin MYOG

Papain

PAPN

αβ

Ribonuclease

RIBO

αβ

Flavodoxin

FLAV

αβ

Glyceraldehyde-3-

phosphate

dehydrogenase

GPDH

αβ

Prealbumin

PREA

Subtilisin BPN

SUBN

αβ

Ttriosephosphate

isomerase

TPIS

αβ

R1 from E. coli

ECOR

αβ

Poly-glu PGAC

Poly-glu (random) PGAR other

Hen lysozyme

LYSM

αβ

Thermolysin

THML

αβ

Poly-glu (random) PGAS other

Poly-glu (random) PGAL other

Polylysine (random) PLYS other

Concanavalin a

CNCA

Beta-LG

BLAC

Human Serum Albumin HSA

Calmodulin CALMOD

Melittin MELI

Tropomyosin TROPO

GCV

100

120

Number of centers

3 8 13 18 23 28 33 38

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

21 22 23 24 25 26 27 28 29

CHYM

CYTC

ELAS

HAEM

LADH

LYSO

MYOG

PAPN

RIBO

FLAV

GPDH

PREA

SUBN

TPIS

ECOR

PGAC

PGA

LYSM

THML

PGAS

PGAL

PLYS

CNC

BLAC

Fig. 1. Graph of GCV as function number of RBF centers for all proteins.

The graph shows that most M values have a minimum value at about 25. Thus this

value was chosen for all spectra. Having chosen all parameters the RBF network was

trained for each of the spectra. The regularization parameter λ was estimated for each

of the spectra. The output of the network was the weights, w, which is a vector with

25 values.

The new input space, W, is a matrix combining the weights of all the spectra and is

used to train different multi-class SVMs. The first approach uses the “One vs. One”

method, the second one is the “One vs. Rest”, and the third is the DAGSVM. Finally

the last method takes into account the properties of the spectra for each of the classes.

For each method the optimum kernel and the corresponding parameters values are

found using the Leave-One-Out cross validation process. This procedure consists of

removing from the training data one element, constructing the decision rule on the

basis for the remaining elements and then testing on the removed element. This

method produced an almost unbiased estimator [18].

To apply the “One vs. One” method, ten binary classifiers have to be constructed.

The optimal kernel was found to be the RBF function with the width parameter set to

0.0031 and the regularization parameter C set to 100. However, the results were not

very satisfactory as only 60% of the proteins are classified correctly.

The DAGSVM requires the same number of binary classifiers; however it

produced much better results. For this method, again the kernel was chosen to be the

RBF function but with the width parameter set to 0.05 and C set to 100. The results

show that 80% of all proteins were correctly classified. In addition, all of the β and

“others” proteins are correctly classified.

Applying the “One vs. Rest” multi-class scheme to the data produced even better

results and only five binary classifiers are needed. The optimum kernel was found to

be again the RBF function with the width parameter set to 0.0016 and C set to 100.

Only three of the proteins where misclassified (90% correctly classified). As in the

DAGSVM method, all the proteins that belong to either β or “others” class were

correctly classified.

In the last method, the combined properties of the CD spectra were taken into

account. As mentioned at the introduction the three classes α, α + β, α/β have similar

spectra, thus one binary classifier was employed to distinguish them from “others”

proteins and the β proteins. A second classifier was used to distinguish β proteins,

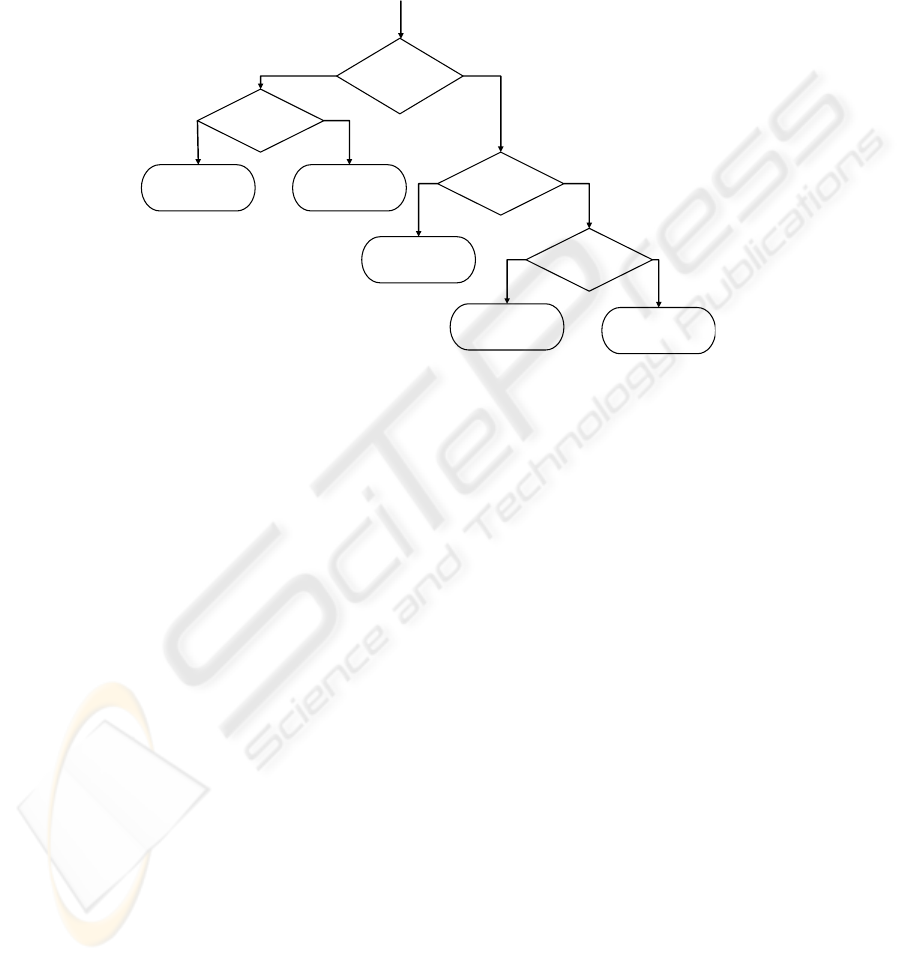
from the “others” proteins. The third classifier was employed to separate the proteins

belonging in class α/β. Thus the last one is used to separate the classes α and α + β

Thus this method only uses four binary classifiers. Fig. 4 summaries the above

procedure.

Fig. 2. Flow chart for classifying proteins using SRCD spectra.

The two first SVM binary classifiers are linear with C set to 1. The third one is a

non-linear classifier. The kernel function was chosen to be a Gaussian function and

the optimal width parameter was found to be 0.1 and C is again set to 100. The last

classifier is also non-linear but with the kernel function chosen to be polynomial in

the power of 11.

This method produced the best results with only two proteins misclassified. The

first one is the T4 lysozyme (LYSO), which is α + β protein but it is classified as α

protein. This is due to the fact that although the T4 lysozyme is very helical at 67%,

there are some β-sheets (10%). This protein is classified as α protein in the CATH

database, thus it is marginal. In addition there is no other similar protein in the

training set. The system was also unable to classify the Cytochrome C (CYTC), which

is α protein. The protein falls on the hyperplane separating the classes α and α + β.

This is due to its relatively small value of alpha helix fraction and also again there is

not a similar protein in the set.

5 Conclusion

This paper presents a new approach to predict the tertiary structure class of proteins

from synchrotron radiation circular dichroism (SRCD) spectra. The three most

commonly used multi-class SVM schemes were employed. Good results were

achieved using the “One vs. Rest” method where only three proteins where

misclassified. However the results were improved further when we take into account

Is it in class

“others” or

eta?

Is it in class

β?

Test protein belongs

to class “others”.

Test protein belongs

to class β.

Test protein

Is it in class

α/β?

Is it in class

α+β or in α?

Test protein belongs

to class α/β.

Test protein belongs

to class α+β.

Test protein belongs

to class α.

the properties of the spectra in each class. With this method only four binary

classifiers were employed and only two proteins where misclassified. In addition the

system was able to classify correctly all of the proteins belong to either β, or α/β or

“others” class. The experimental determination of additional protein CD spectra is in

progress. This will, hopefully, provide a more balanced training set and so enable

more accurate prediction of protein structures.

References

1. Wallace, B.A. and R.W. Janes, Synchrotron radiation circular dichroism spectroscopy of

proteins: secondary structure, fold recognition and structural genomics. Current Opinion in

Chemical Biology, 2001. 5(5): p. 567-571.

2. Whitford, D., Proteins : structure and function. 2005, Chichester, West Sussex, England ;

Hoboken, NJ: John Wiley & Sons c2005.

3. Fasman Gerald, D., Circular dichroism and the conformational analysis of biomolecules.

1996, New York ; London: Plenum Press.

4. Manavalan, P. and W.C. Johnson, Sensitivity of Circular-Dichroism to Protein Tertiary

Structure Class. Nature, 1983. 305(5937): p. 831-832.

5. Venyaminov, S.Y. and K.S. Vassilenko, Determination of Protein Tertiary Structure Class

from Circular Dichroism Spectra. Analytical Biochemistry, 1994. 222(1): p. 176.

6. Scholkopf, B. and A.J. Smola, Learning with kernels : support vector machines,

regularization, optimization, and beyond. Adaptive computation and machine learning.

2002, Cambridge, MA ; London: MIT Press.

7. Branden, C. and J. Tooze, Introduction to protein structure. 1999, New York: Garland

c1999.

8. Murzin, A.G., et al., SCOP: A Structural Classification of Proteins Database for the

Investigation of Sequences and Structures. Journal of Molecular Biology, 1995. 247(4): p.

536.

9. Pearl, F., et al., The CATH Domain Structure Database and related resources Gene3D and

DHS provide comprehensive domain family information for genome analysis. Nucleic

Acids Research, 2005. 33(Supp): p. D247-D251.

10. Broomhead, D.S. and D. Lowe, Multi-Variable Function Interpolation and Adaptive

network. Complex System, 1988: p. 2:321.

11. Bishop, C.M., Neural networks for pattern recognition. 1995, Oxford: Clarendon Press

c1995.

12. Orr, M.J.L., Introduction to Radial Basis Function Networks. 1996, University of

Edinburgh: Edinburgh, Scotland, UK.

13. Orr, M.J.L. Optimising the Widths of RBFs Radial Basis Functions. in Fifth Brazilian

Symposium on Neural Networks. 1998. Belo Horizonte, Brazil.

14. Vapnik, V., The nature of statistical learning theory. 1995, New York ; London: Springer.

15. Shawe-Taylor, J. and N. Cristianini, Kernel methods for pattern analysis. 2004, Cambridge,

UK ; New York: Cambridge University Press.

16. Friedman, J., Another approach to polychotomous classification. Technical report Stanford

University, UA, 1996.

17. Platt, N.C.J. and J. Shawe-Taylor, Large magin dags for multiclass classification. Technical

report, Microsoft Research, Redmond, US, 1999.

18. Chapelle, O., et al., Choosing Multiple Parameters for Support Vector Machines. Machine

Learning, 2001. 46(1/3): p. 131-160.