Modeling Deceptive Action in Virtual Communities

Yi Hu and Brajendra Panda

Computer Science and Computer Engineering Department

University of Arkansas, Fayetteville, AR 72701 USA

Abstract. Trust and shared interest are the building blocks for most

relationships in human society. A deceptive action and the associated risks can

affect many people. Although trust relationship in virtual communities can be

built up more quickly and easily, it is more fragile. This research concentrates

on analyzing the Information Quality in the open rating systems; especially

studying the way deceptive data spread in virtual communities. In this paper,

we have proposed several novel ideas on assessing deceptive actions and how

the structure of the virtual community affects the information flow among

subjects in the web of trust. Furthermore, our experiments illustrate how

deceptive data would spread and to what extent the deceptive data would affect

subjects in virtual communities.

1 Introduction

Trust aggregation and propagation are attracting much attention in research in open

rating systems [1, 2, 3, 4, 7, 10, 11, 12]. We consider the problem of modeling

deceptive action in the web of trust, which forms the base for the online virtual

community. In such a community, a rumor or deceptive data may affect a group of

people with the spreading of the data. The situation can become worse, when an

adversary subject accumulates reputation gradually and later deliberately releases

some deceptive data, say a rumor about some merchandise. The deleterious effect

may not only be contained in a small range of the network. It may spread among

many other individuals in web of trust. A rumor circulated in a grocery store in a

small town may slowly affect local patrons, while the communication speed and the

number of affected people for the same information in an online community can be

much higher.

One can think of web of trust as a big network as well as a labeled directed graph

where the numerically labeled edges indicate the trust levels between two

corresponding subjects. Although the web of trust can generally be considered as a

connected graph, it has its own characteristics. For example, if we consider all trust

relationships among all subjects in epinions.com as the web of trust, we would find

many different communities based on people who are interested in different

categories of merchandises and who express ratings on them.

This work was supported in part by US AFOSR under grant FA9550-04-1-0429

Hu Y. and Panda B. (2006).

Modeling Deceptive Action in Virtual Communities.

In Proceedings of the 4th International Workshop on Security in Information Systems, pages 125-134

 SciTePress

Evaluation of the effect of deceptive data in order to prevent the trust network from

becoming unusable is critical for the normal operation of the semantic web or simply

an e-commerce web site. This paper addresses the analysis model based on the

structure of the web of trust and shared interest among people. In this paper, we

assume that information flow network is the same as the web of trust. The reason is

that, although generally speaking, information flow network can be totally different

from the web of trust network, the information flow policy then becomes too broad

and less useful in practice. For example, although a rumor releaser can send email to

anyone in the web of trust (in this case unrestricted information flow policy), if people

do not know him personally they will simply discard the email without even further

investigation. Although there’s an exception to this, for example, if the system

administrator of an online community sends out some rumor, almost every user will

believe him. But in this case, it is a role-based trust relationship. In this research, we

do not consider role-base trust or information flow. Interested users may refer to the

research on restricted lattice-based information flow policy [6].

2 Structural Property of the Web of Trust

In order to analyze the spread of deceptive data in the web of trust, a web of trust and

the information flow policy/network are needed. To quantitatively decide the exact

range of the spread of deceptive data, a full specification of web trust is needed. That

is, for each trust relationship, we need to know the exact trust rating. Even this

information is available, because different people have different trust propensity and

trust scales, for instance, “subject A trusts subject B 70%” does not mean the same

degree of trust as “subject C trusts subject D 70%”, it’s very difficult for trust ranking

on an information flow path.

In this paper, we propose a model for qualitatively estimating different affected

areas of the web of trust under the effect of deceptive data. The model only needs the

structural properties of web of trust and shared interest; subjective parameters of web

of trust such as trust ratings and individual trust thresholds are not used.

2.1 The Hierarchical Structure of the Web of Trust

The idea of trust hierarchies is based on the real-word relationship among human

beings. In web of trust, the most trusted ones are his acquaintance, i.e., family

members, closed friends, coworkers, etc. They share many common interests. Also,

each individual may belong to some community. For example, people from one

country may have their own community. All users belonging to the member of an

online forum compose the virtual community. Some people in the same community

share common interests. Each subject in the community has an interest circle for each

topic he is interested in (and we say this subject is the owner of the interest circle).

This interest circle contains all subjects in the community that are interested in this

topic and a message on this particular topic can be flowed to all these subjects directly

or indirectly from the owner of the interest circle. Outside the community, each

individual may belong to some meta-community. For example, people interested in

126

different communities must go along one of these few edges. Thus, the edges

connecting communities will have high edge betweenness.

Fig. 2. Communities in the Web of Trust.

The method for finding the community structure as defined by Girvan and

Newman can only reflect the hierarchical relationship of the vertices in the graph. It

cannot derive the number of communities present in the graph and, thus, is not ideal

for large complex graphs. We observed that the edge betweenness of an inter-

community edge is significantly greater than that of any edge inside the communities.

Based on this property, we designed the following algorithm for detecting the

communities in the web of trust. By using different thresholds, we can also identify

meta-community structures.

Algorithm: Find_Communities

1. Calculate the edge betweenness for all edges in the web of trust.

2. IF there is any edge deleted during community finding procedure

3. Pvalue = the edge betweenness of the deleted edge

4. Cvalue = the highest edge betweenness of the current graph

5. IF (Cvalue/Pvalue > threshold)

6. Delete the edge with the highest edge betweenness

7. ELSE

8. Return connected sub-graphs as communities

9. ELSE

10. Delete the edge with the highest edge betweenness

11. GOTO Step 2.

3 Model for the Spread of Deceptive Data

In the web of trust, when a malicious subject releases any deceptive data, we propose

to identify the spread of the data qualitatively as follows. The first step is to find out

the community/meta-community the malicious subject belongs, this can be achieved

based on the algorithm Find_Communities which is based on the edge betweeness. By

using different threshold in the algorithm, we can identify communities and meta-

communities. Once this structural information is available, we can identify the spread

range of the rumor as per following four hierarchies.

128

1. The acquaintance: The subjects who most easily would be affected are the

acquaintance, which are immediate neighbors of the rumor releaser in the web of

trust. They have the highest possibility of being affected.

2. The interest circle: Rumors with different topics have different spread range.

How the structural property of the web of trust and different topics affect the spread

range is our main concern. We will illustrate this in detail in the following sub-

sections.

3. The community: The community represents the group of densely connected

nodes in the web of trust. Because the formation of trust is based on shared interests

among human beings, the more densely nodes are connected, we can imagine that

more interests they share with each other. Thus the community is the next possible

range for the spread of the rumor.

4. The meta-community: The meta-community represents connected sub-graphs

each of which itself is densely connected. Very often, people in these sub-

communities share interests at a higher level. For example, home electronics meta-

community has digital camera community, home theater community, and others in it.

Thus, rumor can be spread to meta-community, but with the least likelihood.

Fig. 3. Information Flow Based on Interest Propagation.

According to the study of information flow in social groups [5], while viruses tend

to be indiscriminate in infecting any susceptible individual, information is selective

and passed by its host only to individuals the host thinks would be interested in it.

Based on this observation, we propose that in the web of trust, the spread of deceptive

data/rumor is different from the spread of epidemic disease or computer virus. It is

also different from the random walker phenomenon used in many trust ranking

algorithms. For example, in Figure 3, α

releases a rumor to θ, in reality θ will not

blindly send information to all of β

, β

and β

, nor will he forward this rumor

randomly to one of them. When θ receives this information, he may only forward the

information to the subject that is interested in it provided that θ thinks this rumor

might be true. Say θ knows that only β

is interested in this topic, in real world most

likely θ will propagate this information to β

only

3.1 Interest Propagation and Dynamic Interest Vector Tables

Since information is selective, in case some rumor releaser releases deceptive data in

the web of trust, this rumor will seldom be spread and as well trusted by every

subjects in the community where the rumor releaser belongs to. In this research, one

of our primary goals is to find out to what extent the rumor spreads in the community.

129

In order to estimate the worst-case scenario in spread of the rumor, following data

structures are employed.

Every subject has a list of topics that he is interested in and as well as his

acquaintances are interested in. We use I

, t

, …, t

> to represent all the topics

that subject i and i’s acquaintances are interested in. I

is maintained for each subject

in the web of trust. Dynamic Interest Vector Table T

< v

, v

, …, v

> is a table in

which v

is an interest vector which lists all subjects that are interested in t

and a

message on topic t

can be flowed to them directly or indirectly from node i. All nodes

in v

form an Interest Circle of node i on topic t

. Thus, for each topic t

, node i has a

corresponding interest circle. Table 1 illustrates dynamic interest vector tables of the

nodes in Figure 3.

Table 1. Dynamic Interest Vector Tables.

We assume that every node trusts its acquaintance 100% in order to get a

maximum possible spread range. We also assume that every node will send

information only to its acquaintances that are interested in it. It must be noted that for

the same rumor, the spread range will be different for different sender nodes.

The following algorithm is proposed to find out the interest circle, which is

actually the interest vector corresponding to a particular topic. Since each node, N

only communicates with its acquaintance, in its dynamic interest vector table against

each topic it lists all its neighboring nodes that are interested in that topic; if N

itself

is also interested in the topic, N

is also added to the list. In order for node N

to know

what topics other nodes are interested in directly or indirectly, our algorithm will

propagate its interested vector table to all its neighboring nodes. It must be noted that

the whole table need not be propagated; only the topics that the neighboring node

interested in will be propagated. After its neighboring nodes get this table, each of

them will update their local interest vector table by adding subjects interested in

certain topic in its interest list. This procedure runs for every node periodically, thus

after a certain period, node N

will know which other people can be reached if N

sends

out a message on topic t

. Also, we expected that each node’s interests may change

over time, i.e., each node may develop more interests on some other topics, or lose

interest in some previous topics. Following is the algorithm for finding out the interest

circle.

Algorithm: Find_Interest_Circle

1. Initialize I

, t

, …, t

> for node i to contain a list of topics t

, t

, …, t

that i

is interested in.

InterestVec(α

, 1)

InterestVec(α

, 2)

…

InterestVec(α

, m)

InterestVec(

, 1)

InterestVec(α

, 2)

…

InterestVec(α

, n)

InterestVec(

, 1)

InterestVec(θ, 2)

…

InterestVec(θ, i)

InterestVec(

, 1)

InterestVec(β

, 2)

…

InterestVec(β

, j)

…

130

2. Initialize T

< v

, v

, …, v

> for node i, where v

= <i> for 1≤ t ≤ m.

3. Broadcast I

, t

, …, t

> to all neighboring nodes of node i.

4. Broadcast T

, v

, …, v

> to all neighboring nodes of node i.

5. Wait for incoming I

, t

, …, t

> and T

, v

, …, v

> sent from any node j

of node i’s neighboring node.

6. After node i received I

, t

, …, t

> and T

, v

, …, v

> from node j, do

operation:

//add j’s interested topic to I

, t

, …, t

> = I

, t

, …, t

> ∪ {t

| t

∈ I

- I

∩I

and j ∈ v

} .

//add a new interest vector containing j to T

for each of j’s interest topic is

not yet in T

For each t

∈{t

| t

∈ I

- I

∩I

and j ∈ v

, v

, …, v

> = T

, v

, …, v

> ∪ { j }

//add a subject that’s not i’s neighbor but interested in i or j’s interest topics

For each row v

∈ T

, v

, …, v

> where 1≤ k ≤ m

If (t

= t

), then v

= v

∪ v

, where 1≤ k ≤ n

//if j is no longer interested in certain topics, remove j from v

in T

For each row v

∈ T

, v

, …, v

> where 1≤ k ≤ m

If (j ∈ v

) and t

∉ I

, t

, …, t

= v

- {j}.

7. Goto step 3

Note: At any run time of the algorithm, v

contains all currently found subjects in

the interest circle of node i based on topic t

. This interest circle is the maximum

possible spread range for the rumor on topic t

sent by node i.

3.2 Experimental Results

Our experiments are conducted in a web of trust testbed which models trust and

interest decay among the nodes. The interest decay represents the average percentage

of interests not shared between a node and its neighboring nodes. That is, if node i to

node j’s interest decay is 15%, then node i shares 85% interest topics with node j. In

order to observe the extent to which the different community structure and interest

decay affect the spread of deceptive data, we use some baseline parameter in Table 2

for modeling our base model of web trust. By changing one parameter at a time, we

got some interesting results on spreading of deceptive data.

Our experiments proceeded as follows. In each test, a node is randomly selected as

rumor releaser. It knows its neighbors’ interest topics and only sends the rumor to its

neighbors that might be interested in the rumor. Once a neighbor receives the rumor,

he will give it a trust ranking. If the trust ranking is above the trust threshold, the

rumor will be sent to his neighbors that are interested in the rumor. Otherwise, he will

discard it. In order to estimate the maximum spread range, in our simulation, we

assume that each subject fully trusts its neighbors.

131

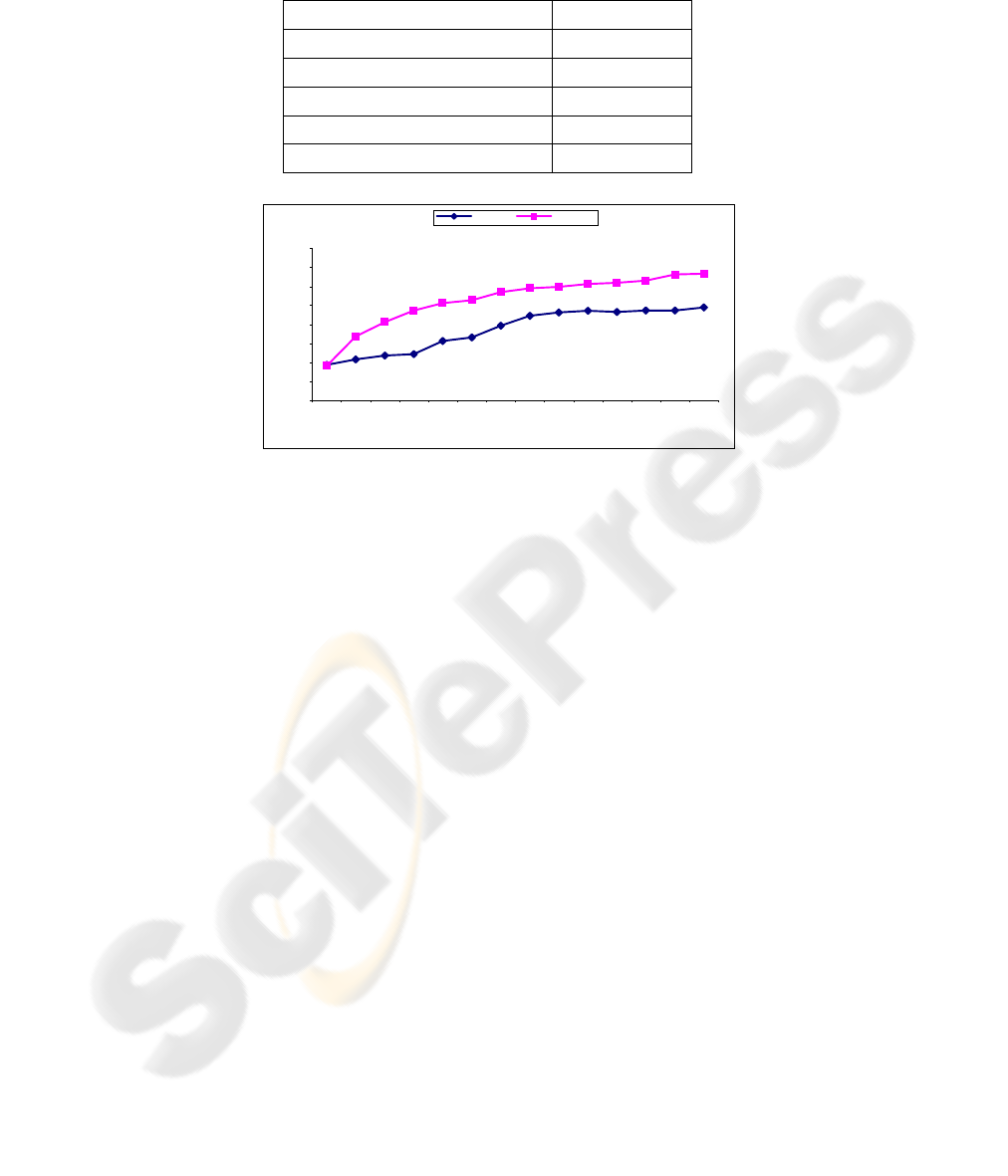
Table 2. Baseline Parameters for Our Web of Trust Test Bed.

Parameter Values

indegree 5

outdegree 5

interest-decay 30%

outdegree of rumor releaser 3

Number of Nodes 5000

100

200

300

400

500

600

700

800

1 2 3 4 5 6 7 8 9 10 25 50 75 100

Outdegree of rumor releaser

Number of nodes affected

1000 nodes 5000 nodes

Fig. 4. Relationship between Number of Nodes Affected and Outdegree of Rumor Releaser.

Misconception 1: In order to significantly increase the spread of the deceptive data,

simply send the rumor to as many people as you know. The number of people

affected by the rumor increases linearly with the increase in the number of the

neighbors of the rumor releaser.

Our experiment proved that the about misconception is not true. Although

increased outdegree of the rumor releaser can contribute to the augment of affected

nodes, the result depends on the average degree of the nodes in the web of trust. In

Figure 4, when the outdegree of the rumor releaser increases from 1 to average node

outdegree (which is 5 in our experiment), it does cause the affected nodes to increase

almost linearly (actually, this also depends on interest decay). However, if the

outdegree of the rumor releaser continues to increase, the spread range only increases

very slowly. For example, the difference in the number of affected nodes from 10-

outdegree and 100-outdegree rumor releasers is only 18 for a 1000-node community.

Misconception 2: The number of affected nodes increases linearly with the

increase of the number of nodes in the community.

Figure 4 and Figure 5 show that misconception 2 is only partially true. With all

other parameters remaining the same, the increase in the number of nodes in the

community only contributes insignificantly to the number of affected nodes. For

instance, as Figure 4 depicts, with the outdegree of the rumor releaser being 10, the

difference in number of affected nodes is only 141 between a 1000-node community

and a 5000-node community. Figure 5 also shows that by simply adding number of

nodes in a community without changing other parameters, the number of affected

nodes change insignificantly. Figure 6 illustrates that only when interest decay is very

132

low, e.g. 10%, the number of nodes affected increases significantly with the increase

of the number of nodes in a community.

100

150

200

250

300

12345678910

Average outdegree of all nodes

Average number of nodes affected

1000 nodes 5000 nodes

Fig. 5. Relationship between Number of Nodes Affected and Average Outdegree of all Nodes.

1000

2000

3000

4000

5000

6000

0% 10% 20% 30% 40% 50% 60% 70% 80% 90%

Interest decay

Number of nodes affected

1000 nodes 5000 nodes

Fig. 6. Relationship between Number of Nodes Affected and Interest Decay.

Fact: How actively each member involves in the community activity and whether

they have similar interests is the number one important factor when evaluating the

spread of rumor in the community.

Figure 6 shows that when the interest topics people share with each other in a

community increases, i.e., the interest decay decreases, the effect of the rumor

becomes more significant. It can be seen from Figure 6 that in a 5000-node

community, the number of affected nodes is 1254 with the interest decay value of

20%. Whereas, when the interest decay is 10%, the number of affected nodes in the

community is 4483, a 260% increase.

4 Conclusions

This paper studies the problem of evaluating the spread of deceptive data based on

structural property of web of trust and the shared interest between subjects in the web

of trust. Our model proposed structural characteristics of web of trust such as meta-

community, community, and interest circle to illustrate how the structural analysis of

133

web of trust can help evaluate the effect of spreading deceptive data. Our experiments

show that the amount of similar interests the members in the community have and the

amount of their active involvement in the community are the primary factors in

deciding the range of spread of the rumor.

Acknowledgements

We are thankful to Dr. Robert. L. Herklotz for his support, which made this work

possible.

References

1. M. Richardson, R. Agrawal, and P. Domingos. Trust Management for the Semantic Web.

In Proceedings of 2

International Semantic Web Conference, USA, October 20-23, 2003.

2. R. Guha. Open Rating Systems. http://tap.stanford.edu/wot.pdf.

3. R. Guha, R. Kumar and P. Raghavan and A. Tomkins. Propagation of Trust and Distrust. In

Proceedings International WWW Conference, New York, USA, 2004.

4. B. Friedman, P. Kahn, and D. Howe. Trust Online. Communications of the ACM.

December 2000/Vol. 43, Issue 12.

5. F. Wu, B. Huberman, L. Adamic, and J. Tyler. Information Flow in Social Groups. In

Proceedings of CNLS conference on Networks, Santa Fe, NM, May 2003.

6. D. Denning. A Lattice Model of Secure information Flow. Communications of the ACM,

May 1976/Vol.19, Issue 5.

7. L. Xiong and L. Liu. PeerTrust: Supporting Reputation-based Trust for Peer-to-Peer

Electronic Communities. IEEE Transaction on Knowledge and Data Engineering, Vol. 16,

No. 7, July 2004.

8. M. Girvan and M. Newman. Community Structure in Social and Biological Networks. In

Proceedings of National Academy of Sciences, 2001.

9. L. Freeman. A Set of Measures of Centrality Based on Betweenness. Sociometry 40, page

35-41, 1977.

10. B. Yu and M. P. Singh. An Evidential Model of Distributed Reputation Management. In

Proceedings of the first international joint conference on Autonomous agents and

multiagent systems, 2002.

11. B. Yu and M. P. Singh. Searching social networks. In Proceedings of the 2nd International

Joint Conference on Autonomous Agents and MultiAgent Systems. (AAMAS), July 2003.

12. D. Dutta, A. Goel, R. Govindan, and H. Zhang. The Design of A Distributed Rating

Scheme for Peer-to-peer Systems. In Workshop on Economics of Peer-to-Peer Systems,

2003.

134