Requirements-Driven Automatic Configuration of

Natural Language Applications

Dan Cristea

1,2

, Corina Forăscu

1,3

, Ionuţ Pistol

University “Al. I. Cuza” of Iaşi, Faculty of Computer Science

Institute for Computer Science, Romanian Academy, Iaşi – Romania

Institute for Artificial Intelligence, Romanian Academy, Bucharest – Romania

Abstract. The paper proposes a model for dynamical building of architectures

intended to process natural language. The representation that stays at the base of

the model is a hierarchy of XML annotation schemas in which the parent-child

links are defined by subsumption relations. We show how the hierarchy may be

augmented with processing power by marking the edges with names of

processors, each realising an elementary NL processing step, able to transform

the annotation corresponding to the parent node onto that corresponding to the

child node. The paper describes a navigation algorithm in the hierarchy, which

computes paths linking a start node to a destination node, and which

automatically configures architectures of serial and parallel combinations of

processors.

1 Introduction

In this paper we propose a methodology that allows for the automatic configuration of

architectures of serial and parallel combinations of natural language (NL) processors,

each able to perform an elementary transformation to an input file. The input and

output of the modules (between the processing steps) are XML annotated files.

GATE [1], [2] is an extremely versatile environment for building and deploying

NLP software and resources. It allows for the integration of a large amount of built-

ins in new processing pipelines that can be put to work on single documents or

corpora. In order to assemble a pipeline the user is instructed to select the modules

(called resources in GATE) needed as parts of the processing chain, in the correct

processing order, and to instantiate their parameters. When all these are done, the

configured chain of processes may be put to work on an input file, with the result of

obtaining an output file, XML annotated. The model we propose is able to automatise

the process of assembling architectures of modules, which is manually performed in

GATE. The automatically configured architecture will combine processing steps and

filtering steps. The processing steps add information while filtering steps remove

information. Conforming to the proposed model, the input and output annotation

schemas can be automatically classified on a pre-existing hierarchy, their places

triggering the whole computation of the steps involved in the transformation.

Our approach further extends the Cristea and Butnariu’s model of operators based

on a hierarchy of annotation schemas [3]. In their model, XML annotation schemas

Cristea D., For

ascu C. and Pistol I. (2006).

Requirements-Driven Automatic Conﬁguration of Natural Language Applications.

In Proceedings of the 3rd International Workshop on Natural Language Understanding and Cognitive Science, pages 47-56

DOI: 10.5220/0002481200470056

 SciTePress

are nodes in a directed acyclic graph, in which the hierarchical links are subsumption

relations between schemas. The model allows classification, simplification and

merging operations to be performed on files observing the restrictions of the

annotation schemas that are included in the hierarchy.

We describe how the graph of annotation schemas may be augmented with

processing power by marking edges, linking parent nodes to child nodes, with names

of processors, each realising an elementary NL processing step. On the augmented

graph, three operations are defined: simplification, pipeline and merge. We present

then a navigation algorithm in this hierarchy, which computes paths between a start

node, corresponding to an input file, and a destination node corresponding to an

output file. These computed paths correspond to sequences of operations, which are

equivalent to architectures of serial and parallel combinations of NL processors.

When an input file is given to a system that implements these principles, and the

requirements of an output annotation are specified as the destination node, first the

XML annotation schema of the input file is determined, then this schema is classified

onto the hierarchy, becoming the start node, then the expression of operations

corresponding to the minimum paths linking the start node to the destination node is

computed (the architecture), and finally the input file is given to this architecture,

resulting in the expected output file.

Section 2 of the paper reviews the hierarchical model of annotation schemas, while

section 3 presents the hierarchy augmented with processing power. In section 4, the

operations associated to the augmented graph are defined. Section 5 presents the

algorithm that computes the sequence of operations, displays some examples and

briefly describes an implementation of the algorithm. In section 6 the feasibility of the

approach in practical settings is discussed.

2 The Graph Representation of Annotation Schemas

In [3], different layers of annotation over a corpus are represented as a hierarchy. A

node in the hierarchy is an annotation schema. It contains a list of XML tags, each

characterised by a name, a list of attributes, and possible restrictions encumbered by

identifying attributes values of different tags in the hierarchy. The parenthood

relationship places the schemas described in this way in a hierarchy, which is a

directed acyclic graph whose node names are unique symbols. If a node A is directly

linked to a node B, then it is said that A subsumes B in the hierarchy (therefore B is

a descendent of A). This happens if and only if:

- any tag-name of A is also in B;

- any attribute in the list of attributes of a tag-name in A is also in the list of

attributes of the same tag-name of B;

- any restriction which holds in A also holds in B.

The subsumption relation indicates that each node in the hierarchy inherits all

features (seen here as tags and their attributes) of all of its parents. So, if A subsumes

B, B is an annotation schema which is more informative than A and/or defines more

constraints. In general, either B has at least one tag-name which is not in A, and/or

there is at least one tag-name in B such that at least one attribute in its list of attributes

is not in the list of attributes of the homonymous tag-name in A, and/or there is at

least one constraint which holds in B but which doesn’t hold in A. The subsumption

relation is transitive, reflexive and asymmetrical.

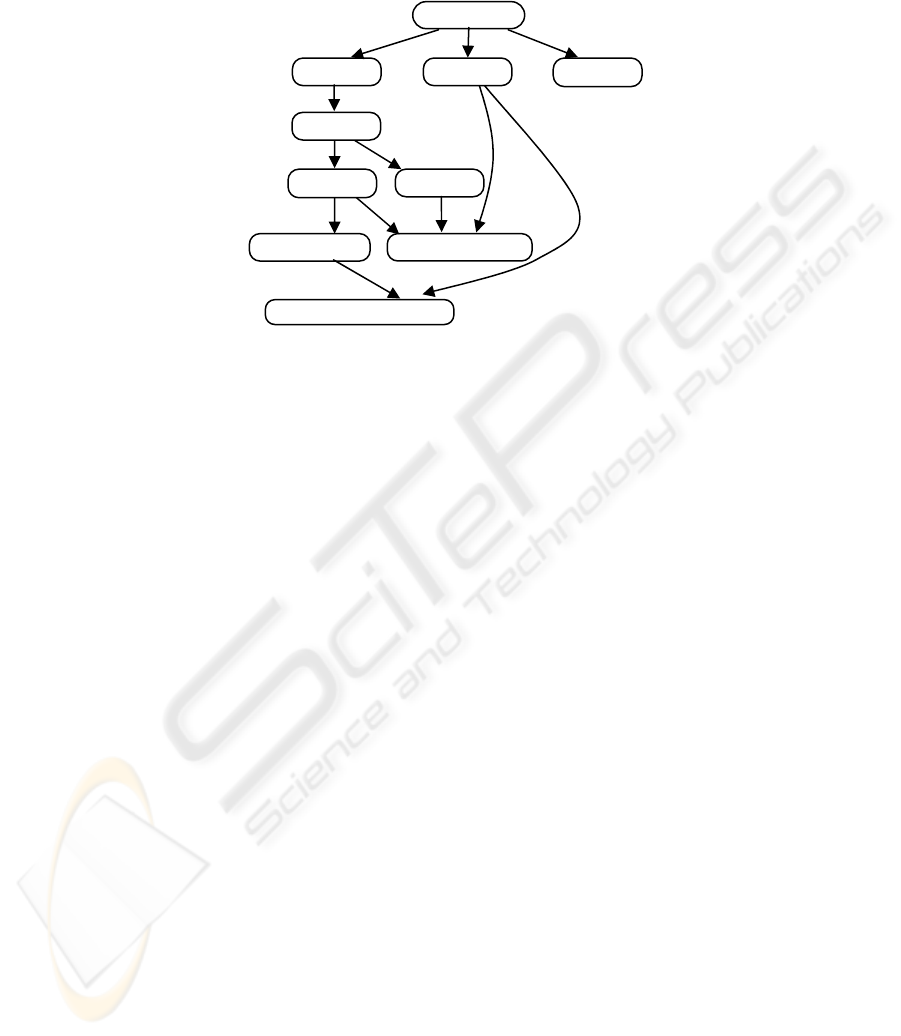
Fig. 1. Example of a hierarchy of schemas (adapted after an example from [3]).

Figure 1 shows an example of a hierarchy of schemas describing different layers of

annotation useful for many NLP applications. SCH-ROOT represents the “empty”

annotation (no tags). Immediately under this trivial schema, three schemas, SCH-

TOK, SCH-SEG and SCH-PAR are placed. SCH-TOK identifies tokens and marks

word lemmas, SCH-SEG marks borders between elementary discourse units, while

SCH-PAR marks paragraphs. SCH-POS, placed under SCH-TOK, does not contribute

with new tags but it complements the token tag with an attribute that indicates the

part-of-speech. SCH-POS is a parent for both SCH-NP and SCH-VP schemas. These

mark noun phrases (NPs) and, respectively, verb phrases (VPs). Then, SCH-COREF,

placed under SCH-NP, marks anaphoric links between co-referential NPs. SCH-SEG-

NP-VP is a schema marking simultaneously noun phrases, verb phrases and discourse

units boundaries. It adds no new markings to those inherited from its three parents.

Finally, SCH-COREF-IN-SEG is a schema in which the co-references and segment

boundaries are marked.

An example of an XML file observing the restrictions of the SCH-COREF-IN-

SEG node is shown in Figure 2.

3 Marking the Edges of the Graph with Processor Names

Modern software engineering design uses interchangeable modules, which are

interconnected in complex processing architectures. In NLP, this approach has proven

advantages with respect to reusability, and language and application independence. In

such a view, each module has inputs, outputs and accesses resources. In order for the

modules to be truly interconnectable, each of the module’s inputs and outputs must

observe the constraints of certain annotation schemas. Usually the language and,

sometimes, application dependence of a module is given by the specific set of

resources it accesses. For instance, a POS-tagger, runs the same algorithms on differe-

SCH-NP

SCH

SEG

SCH-ROOT

SCH-TOK SCH-PAR

SCH-POS

SCH-VP

SCH-COREF

SCH-COREF-IN-SEG

SCH-SEG

nt sets of language models in order to tag documents for POS in different languages.

For the system builder, the real functioning of a module can be obscured in a black

box, since is it fully determined by the triplet: input, output and resources. This is

equivalent with saying that given a triplet of schemas, characterizing the input, the

resources and the output, a module should exist which produces as output a file

observing the restrictions of the output schema, whenever it receives as input a file

observing the restrictions described by the input schema, and accesses resources

observing the resources schema. This way, the hierarchy of annotation schemas

becomes a graph of interconnecting modules.

More precisely, if a node A subsumes a node B (see Figure 3), there should be a

process which takes as input a file observing the restrictions imposed by the node A

and produces as output a file observing the restrictions imposed by the node B. While

doing this type of processing, the module might make use also of some resources.

<?xml version="1.0" encoding="ISO-8859-1" ?>

<ROOT>

<TOK id="t2" pos="N" lem="Winston">Winston</TOK>

</NP>

<TOK id="t4" pos="ING" lem="dream">dreaming</TOK>

</NP>

<TOK id="t7" pos="N" lem="mother">mother</TOK>

</NP>

</SEG>

</NP>

</SEG>

</NP>

<TOK id="t13" pos="V" lem="think">thought</TOK>

</SEG>

<TOK id="t19" pos="NUM" lem="eleven">eleven</TOK>

<TOK id="t20" pos="A" lem="years_old">years_old</TOK>

</NP>

</SEG>

</ROOT>

Fig. 2. Example of annotation.

However, in our graphical notations and the considerations to follow, only the input-

output relations will be retained.

Fig. 3. Equivalence between the subsumption relation and a processing step.

Let’s note that the directionality of a process, as attached to an edge of the graph, is

that of the subsumption relation. So, if node A subsumes node B, then the hierarchical

link is from A to B (from the parent to the descendant). In our figures this will be

marked by oriented edges (arrows). To mark the difference between edges denoting

subsumption relations and edges denoting processing, we will mark with thin arrows

the subsumption relations and with labelled thick arrows processing steps, where the

labels indicate the names of the processes. We will call a graph (or hierarchy) of

annotation schemas on which processing modules have been marked on edges as

being augmented with processing power (or simply, augmented).

Fig. 4. The hierarchy in Figure 1 augmented with processing power.

Sometimes the existence of a process attached to an edge in the graph depends on

the existence of adequate resources. For instance, one may have access to an

automatic tagger, but it will not be able to apply it for a language L because of the

lack of a language model (a resource) adequate for that language. This way, in a

repository of resources and instruments dedicated to NLP, the maximal graph of

annotation schemas hosted can have different instantiations for different languages,

depending on the existence (or absence) of adequate resources. Figure 4 represents the

SCH-PAR

SCH-COREF-IN-SEG

SCH-VP

SCH

SEG

SCH-ROOT

SCH-NP

SCH-COREF

SCH-TOK

SCH-POS

SCH-SEG

tokenise

POS-ta

NP-chunke

VP-chunker

mente

∅

paragraph finder

∅

resources

subsumption relation

process p

input

output

hierarchy of schemas from Figure 1, augmented with processing power. The names of

processes are marked on some edges and the symbol ∅ marks the empty process (no

contribution of new tags/attributes). When multiple ∅ edges enter into the same

destination node, the significance is that its annotation represents the merge of all

annotation schemas of the source nodes.

4 Operations in the Augmented Graph

If, in the hierarchical graph of schemas, navigation in the graph allows for the

classification of files in the hierarchy, the simplification of annotations and the

merging of annotations, as described in [3], in the graph augmented with processing

power, navigation allows for the automatic identification of processing steps. Any

process resulting from this computation is a combination of serial processing with

merges. Unlike GATE, which allows only pipeline processing, in which the whole

output of the preceding processor is given as input to the next processor, in our model

a combination of branching pipelines may result.

Once the computation of steps is done using the augmented hierarchy, then the

computed process can be applied on an input file, eventually producing an output

file. These files comply with the restrictions encoded by a start node and,

respectively, a destination node of the hierarchy.

A processing task is defined by a pair of annotation schemas, start and destination.

Transposed on the processing graph, provided the two schemas are represented as

nodes in the graph and since the graph is connected, there should always be at least

one path connecting these two nodes. The paths found are made up of oriented edges,

and, as we will see, it is important if the orientation of the edges is the same as the one

of the path or no.

We will describe later in this section three operations associated with the computed

paths. Due to these operations, the otherwise static set of alternative paths linking a

start node to a destination node determine a set of alternative processing paths or

flows, which represent dynamically configured architectures. There are two ways to

look at flows as processes: as applied to nodes of the graph and as applied to files. A

flow transforms an input (node or file) by adding or deleting some mark-ups, seen as

definitions in a node (schema) and as actual annotation in a file. The term “flow”

comes easily if we imagine that the information actually “flows” through the edges of

the graph, while also producing changes in the input files. Different examples of

flows, linking start nodes with destination nodes, are sketched in Figure 5 in thin,

interrupted arrows.

More precisely, a flow must be seen as summing-up sequences of processing steps.

We will denote by f(x) the flow applied to the input node, or file, x. So, y=f(x) means

either that the destination node y is obtained by applying the flow f to the start node x,

or that the output file y results by the application of the flow f to the input file x. All

three operations which will be defined below produce flows. Trivially, an empty flow,

denoted by f

∅

, leaves the input unmodified. So, f

∅

(x)=x, for any node or file x. The

way in which we will define the computation of flows (in section 5), so that if A and B

are the start and destination nodes in a graph, will make that exactly one flow f should

exist such that B=f(A). Flows can be combined, such that it is possible to have B=

(A)). This notation inspires the generalisation of a flow as applying to flows

instead of nodes or files. Indeed if a node B is placed along a path from A to C, we

may say that the flow that transforms A onto B combines with the one that transforms

B onto C to produce the flow that transforms A onto C. As such, we may see the input

of the second flow as being the first flow, instead of the intermediary node.

In the rest of this section we will give the definitions of the three operations:

Fig. 5. Examples of processing paths: thin, black, interrupted arrows represent processing

paths, superposed over thick, grey, continuous arrows, representing subsumption relations.

simplification, pipelining and merging. We say that a node A is simplified to B, and

we write B=S

(A), if A and B are both placed on a path from the start to the

destination node, in this order, and B subsumes A. When a file corresponding to the

schema A is simplified to B, it will lose all annotations except those imposed by the

schema B. In Figure 5a, we have B=S

(A), and on Figure 5b it holds that C=S

(A) and

E=S

(A). In accordance with our discussion on flows above, we may look at S

as a

flow, which allows us to apply it to a node, to a file or to another flow.

If, on a path from the start node to the destination node in the augmented graph,

there is an edge linking a node A to a node B which is marked with a process p, we

say that A pipelines to B by p, and we write B = A>p. Equally, when a file

corresponding to the schema A is pipelined to B by p, it will be transformed by the

process p onto a file that corresponds to the restrictions imposed by B. Finally,

according to the discussion on flows, we may consider “pipelines by p” an operation

which is applied to a flow to produce a flow. Pipelining with an empty process ∅

leaves the input unmodified, while pipelining the empty flow with a process yields the

flow consisting of that process. In Figure 5b it holds that B=C>b and B=E>a>c.

The merge operation can be defined in nodes pointed by more than one edge on the

hierarchical graph. If f

, …, f

, are flows entering a node A, we say that flows f

, …, f

merge into A and we write A= f

| … | f

. For instance, in Figure 5b we have B=C>b

| E>a>c. Merging a flow f with the empty flow f

∅

leaves f unchanged.

With these definitions, for the graph of Figure 5b it holds that B=S

(A)>b |

(A)>a>c, and for the graph of Figure 5c it holds that B=((A>c | S

(A)>a>d)>e |

(A)>b>f)>g.

5 Computation of Flows

We give below the Compute-Flow algorithm. The notations used are as follows:

function CF(x,y) receives as input a pair of nodes start-destination and returns that

flow which applied to x outputs y; subsumes(x,y) is a predicate function which

applied to two nodes evaluates to true if and only if x subsumes y on the graph;

simplify(x,y) expresses that the node y is simplified to x and returns a flow;

pipeline(f,p), with f a flow and p a process, expresses that the flow f is

pipelined with the process p and returns a flow; merge(f

) expresses the

merging of flows f

and f

and returns a flow, and f

∅

is the empty flow.

function CF(st,de)

if (st equals de) then return(f

∅

);

else if (subsumes(de,st)) then return(simplify(de,st));

else if (there is just one node n such that

n pipelines to de by a process p) then

return(pipeline(CF(st,n),p));

else { expr := f

∅

;

while (there still exists a node n pipelining to de

by a process p) do

expr := merge(expr, pipeline(CF(st,n),p));

return(expr); };

Note that in the above notation of the function CF the input is a pair of nodes start-

destination and the output is a computed flow, as an expression of simplify-pipeline-

merge operators. In order to make the computed flow to apply to an input file, the

input file must be given to the result of the computation of a call to the function CF.

Following, we will exemplify with several cases:

- for the graph depicted in Figure 5a, subsumes(B,A) is true, therefore the

algorithm CF(A,B) returns simplify(B,A);

- for the graph in Figure 5c, using short notations for Pipeline (P), Merge (M), and

Simplify (S), the recursive evaluation proceeds as follows, in which the ⇒ sign

should be read as “evaluates to”:

CF(A,B) ⇒ P(CF(A,G),g) ⇒ P(M(P(CF(A,E),f),P(CF(A,F),e)),g) ⇒

P(M(P(P(CF(A,C),b),f),P(M(P(CF(A,A),c),P(CF(A,D),d)),e)),g)

⇒ P(M(P(P(S(A,C),b),f),P(M(P(A,c),P((CF(A,C),a),d)),e)),g)

⇒ P(M(P(P(S(A,C),b),f),P(M(P(A,c),P(P(S(A,C),

a),d)),e)),g).

This expression is identical with the one depicted in section 4 in an abridged form;

- for the graph in Figure 1, if in the call to the function CF the node st is

SCH-

ROOT

and the node de is SCH-COREF, the meaning of the compute request CF(SCH-

ROOT,SCH-COREF)

is that, starting from a raw text one should get annotations for co-

referential anaphora, but including also the marking of tokens, their part-of-speeches,

and the noun phrases – which usually count as referential expressions. The computed

flow is, in the abridged notation for pipelines:

SCH-ROOT > tokeniser > POS-

tagger > NP-chunker > AR

, where tokeniser is the process which tokenises a

raw text, the

POS-tagger adds part-of-speech markings to a tokenised text, the NP-

chunker

marks NPs on a POS-tagged text and AR is the module doing anaphora

resolution on a file having NPs marked;

An implementation of the hierarchy model has been developed for a portal

intended to act as a repository for Romanian language resources and NLP tools. The

current implementation performs automatic classification, simplification and merging.

Presently, a number of modules locally developed have been linked with the edges of

an existent graph of schemas. The coupling with the GATE style of processing is

under study. The final machinery will develop into a portal displaying on-line

processing, to which a user can send its own files, he indicates the desired final

annotation and receives the output file.

6 Discussion

The proposed approach has an apparent drawback which is the large diversity of

annotation schemas which could appear in different applications. This could amount

to a huge graph of schemas if the ambition is for exhaustiveness. However, the need

for standardisation is evident nowadays and has been very clearly stated in many

contexts, for instance (Ide et al., 2003). The more and more common use of

international standards for the annotation of documents, such as TEI and CES/XCES,

will make widely applied standardisation a reality. Moreover, Semantic Web, with its

tremendous need for interconnection and integration of resources and applications on

communicating environments, boosts vividly the appeal for standardisation. It is

therefore foreseeable that more and more designers will adopt recognised standards,

in order to allow easy interfacing of their applications. The large acceptance of XML

as an annotation language, the development of a variety of sublanguages based on

XML, and the adoption of encoding standards as TEI and CES in text processing

makes this challenge a reality.

But there is another reason for the drawback to be only apparent. We have seen

already that, by classification, any schema could be placed in the hierarchy. Of

course, classification could increase in an uncontrolled way the number of nodes of

the hierarchy. The proliferation could be caused not so much by the semantic

diversity of the annotations as by the differences in name spaces (names of tags,

attributes and values). Suppose one wants to connect a new file to the hierarchy in

order to exploit its processing power. What s/he has to do is to first classify the file. If

the system reports the result as being a new node in the hierarchy than its position

gives also indications of its similarity/dissimilarity with the neighbouring schemas. A

visual inspection of the names used can reveal, for instance, that a simple translation

operation can make the new node identical to an existing one. This means that the

new schema is not new for the hierarchy, although the set of conventions used, which

make it different from those of the hierarchy, are imposed by the restrictions of the

user’s application. The solution to this incompatibility is not always a despotic

attitude vis-à-vis of the adoption of new notation conventions, but rather a flexible

way of looking at the diversity. Technically, this can be achieved by temporarily

creating links between the new schema classified by the hierarchy, as a new node, and

its corresponding standard in the hierarchy. Processing along such a link is different

than the usual behaviour associated to the edges of the graph. It describes a translation

process, in which the annotation is not enriched, but rather names of tags, attributes

and values are changed. Ideally, the processing abilities of the hierarchy should

include also the capability to automatically discover the translation procedure. This

task is not trivial since it would require that the hierarchy “understands” the intentions

hidden behind the annotation, displaying an intelligent behaviour which is not easy to

implement. This subject could make an interesting trend of further research. Now,

once the entry and exit points in the hierarchy have been determined and translation

links have been devised, all the rest is done by the hierarchy itself augmented with the

processing power in the manner described above. This way, the processing needed to

arrive from the input to the output is computed by the hierarchy as sequences of serial

and parallel processing steps, each of them supported in the hierarchy by means of

specialised modules. Then the process itself is launched on the input file. It includes

an initial translation phase, followed by a sequence of simplifications, pipelines

and/or merges, as described by the computed path, and followed by a final translation,

which is expected to produce the output file.

The linguistic annotations can make use of ontologies as formalised schemas

specifying what can actually be annotated, and hence the annotation schemas can be

considered special cases of semantic annotations with regard to an ontology, such as

the one pursued within the context of the Semantic Web. The formalization of the

annotation schema as ontology, and the use of standard formalisms such as RDF or

OWL to encode it, allows for the reuse of the schema across different annotation

tools. The linguistic annotation model based on ontology offers flexibility in the sense

that it is general enough to be applied in a broad variety of annotation tasks.

Acknowledgments

We thank Valentin Tablan and Dan Tufiş for their suggestions and comments during

the final stages of the elaboration of this paper. This work has been partially

supported by the CEEX research grant ROTEL-29 of AMCSIT and the FP6 IST-

STREP project LT4eL, contract number 027391.

References

1. Hamish Cunningham, Diana Maynard, Kalina Bontcheva, Valentin Tablan. 2002. GATE: A

framework and graphical development environment for robust NLP tools and applications.

In Proceedings of the 40th Anniversary Meeting of the ACL (ACL’02). Philadelphia, US.

2. Hamish Cunningham, Valentin Tablan, Kalina Bontcheva, Marin Dimitrov. 2003.

Language engineering tools for collaborative corpus annotation. Proceedings of Corpus

Linguistics 2003, Lancaster, UK.

3. Dan Cristea and Cristina Butnariu. 2004. Hierarchical XML representation for heavily

annotated corpora. In Proceedings of the LREC 2004 Workshop on XML-Based Richly

Annotated Corpora, Lisbon, Portugal.

4. Nancy Ide, Laurent Romary, Eric de la Clergerie. 2003. International standard for a

linguistic annotation framework. In Proc. HLT-NAACL'03 Workshop on the Software

Engineering and Architecture of Language Technology. Edmonton, Canada.