
CONVERTING TIME SERIES DATA FOR INFORMATION
SYSTEMS INTEGRATION
Li Peng
Software School, Hunan University, Changsha, Hunan, China
Keywords: Integration of heterogeneous data source, data conversion, time-series, calendar.
Abstract: Most enterprises have an autonomous and heterogeneous information system. The same data may be
diversely represented in different information systems. The core of solutions for integrating heterogeneous
data sources is data conversion. One of the major issues of data conversion is how to convert data that
contains temporal information. In this paper I propose a method to effectively convert time-series data
appearing in enterprises. The concept of calendar is integrated into the proposed method. The method is
based on a generalized representing form for data. The converting operations and processes are defined and
presented.
1 INTRODUCTION
Most enterprises have an autonomous and
heterogeneous information system. The same data
may be diversely represented in different
information systems. A typical example is time-
series data which arises very often in applications
like scheduling, manufacturing and process control.
A temporal data “15.4.2005” may be an integer “52”
in another application. The cause of the
inconsistency is that enterprises use various calendar
systems in their applications. The temporal values of
time-series data are determined by the used calendar
system.
The core of solutions for integrating information
systems is data conversion. In this paper, I mainly
discuss how to convert time-series data. Since time-
series data is associated with calendar systems, this
work focuses on converting calendar systems. In
previous related work, the researchers have defined
some calendar operations to derive various user-
defined calendars (Lee, Elmasri and Won, 1996).
However, some complex conversions, for example,
restructuring hierarchical calendars and the
conversion between irregular calendars can not
achieved by using these operations.
In this paper, I propose a systematic method to
convert calendar systems. It contains required
processes and operations. The basis of the
converting method is a generalized representing
form for data, with which all the calendar systems
used in enterprises can be represented in a consistent
form.
This paper is organized as follows. Section 2
gives an overview of calendar systems used in
enterprises. Section 3 presents a generalized
representing form for data. Section 4 describes the
method for converting calendar systems. Section 5
concludes the paper with a summary of the
contributions of this research.
2 CALENDAR SYSTEMS USED
IN ENTERPRISES
A calendar is a temporal model. Each calendar has a
time domain which consists of a sequence of
temporal values. The calendar systems used in
enterprises can be classified in four essential types:
continuous calendar system, discrete calendar
system, complete calendar system and composite
calendar system (Dangelmaier & Ketterer, 1995).
Each type of calendar systems is described as
follows.
The continuous calendar system is modelled as
being isomorphic to the real numbers, with each real
number corresponding to an instant.
The discrete calendar system is modelled as
being isomorphic to the integers. An example of
discrete calendars is “days of January”.
289
Peng L. (2006).
CONVERTING TIME SERIES DATA FOR INFORMATION SYSTEMS INTEGRATION.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 289-292
DOI: 10.5220/0002491702890292
Copyright
c
SciTePress
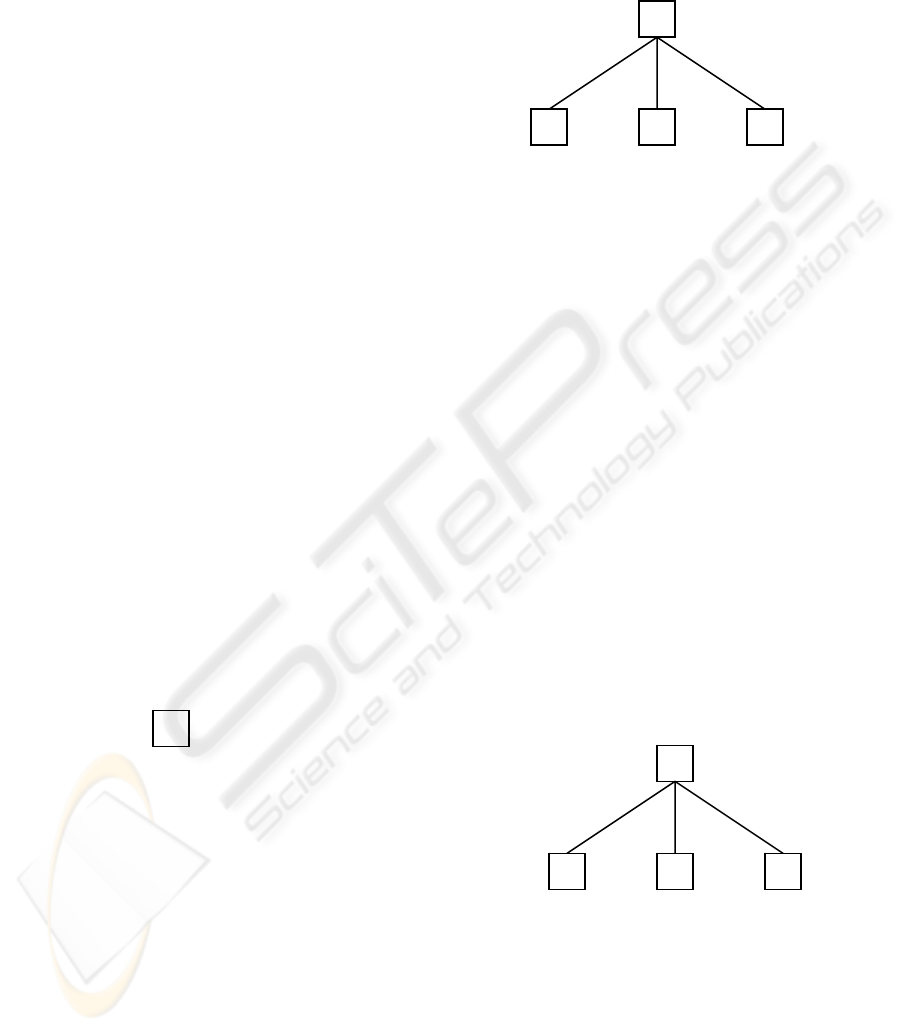
(B)
day
(B)
day
date
(P)
(B)
month
(B)
year
(B)
day
wor
k
-day
(R)
(B)
month
(B)
year
The complete calendar system has no gap. There
are no events which can not be assigned in this
calendar. The Gregorian calendar is an example of
complete calendars.
The composite calendar system has gaps and
consists of a number of time domains. These time
domains can not overlap. The Business calendar, in
which all holidays and weekends have been
excluded, is an example of composite calendars.
A calendar system used in enterprises can be
either one of the four essential types or a
composition of them. For instance, the Gregorian
calendar is a complete discrete calendar.
3 A GENERALIZED
REPRESENTING FORM FOR
CALENDAR SYSTEMS
In many temporal data model, time-series data is
modelled as an attribute that is treated with similar
semantics as other attributes, but with some
extensions to handle characteristics of time-series.
Such an attribute is called a time-series attribute
(Lee, Elmasri & Won, 1996).
Since time-series attribute can have complex
data values and the data values are determined by
the associated calendar, following constructors are
defined to represent various calendar systems.
At first, a node with the token “B” is used to
represent a simple attribute. The domain of a time-
series attribute represented with the node “B” is
integers. In Figure 1, the node “B” represents a
simple attribute “day”.
Figure 1: The note “B” represents a simple time-series
attribute
.
The constructor “P” represents a complete
calendar. The domain of a complete calendar
represented with the constructor “P” is the Cartesian
product of the domains of its components. For
example, the Gregorian calendar is described with
the complex attribute “date”, and “date” can be
described with component attributes “year”,
“month” and “day”. If dom (year) = 2005, dom
(month) =1, and dom (day) = {1, 2, …, 31}, the
domain of the attribute “date” would be the
Cartesian product dom (date) = {(2005, 1, 1), (2005,
1, 2), …, (2005, 1, 31)}. The structure in Figure 2
can be expressed as: date = P: (year, month, day).
Figure 2: The constructor “P” represents a complete
calendar system
.
The constructor “R” represents a composite
calendar. The domain of a composite calendar
represented with the constructor “R” is a subset of
the domain of its corresponding “P” constructor.
Here, the “R” constructor and the corresponding “P”
constructor are described with the identical
component attributes. A Business calendar can be
represented with “R” constructor. In this calendar all
holidays and weekends have been excluded. For
example, if the domain of its corresponding
complete calendar dom (date) = {(2005, 1, 1), (2005,
1, 2), …, (2005, 1, 31)}, the domain of the Business
calendar would be {(2005, 1, 3), (2005, 1, 4), (2005,
1, 5), (2005, 1, 6), (2005, 1, 7), (2005, 1, 10), …,
(2005, 1, 31)}. The structure in Figure 3 can be
expressed as: work-day = R:(year, month, day).
Figure 3: The constructor “R” represents a composite
calendar system.
A calendar is a human abstraction of the physical
time space, and the physical time space is considered
as a hierarchy of totally ordered sets of time
intervals (Lee, Elmasri, Won, 1996). Here I define a
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
290

(B)
day
Figure 4: The constructor “H” represents the hierarchical
structure of a calendar
.
calenda
r
(H)
(B)
month
(B)
year
“H” constructor to describe the hierarchies of
calendar systems. In a hierarchy, the time intervals
at each level are described by using a time unit.
Since the time intervals of each level are partitioned
according to the relationship between the time unit
at this level and the time units at the higher levels,
the domain of each level would be a set of Cartesian
products (except the highest level). As an example,
the hierarchical domain of the Gregorian calendar is
given in Figure 5 and Figure 4 shows the
hierarchical structure. The structure can be also
expressed as: calendar = H:(year, month, day).
The generalized representing form can be
described by a tuple ﹤ constructors, domains of
component attributes, constraints ﹥ , where
constructors are defined above, constraints limit the
values of attributes. For example, a constraint in the
Gregorian calendar is: if month = 2, then dom (day)
= {1, 2, …, 28}.
4 CONVERTING CALENDAR
SYSTEMS
Converting calendar systems mainly involves
following issues: converting a complete calendar to
another complete calendar, converting a complete
calendar to a composite calendar, and converting a
composite calendar to another composite calendar.
In this section, the converting processes are
presented in detail.
4.1 Converting a Complete
Calendar to Another Complete
Calendar
If the time units used in the source calendar and the
time units used in the destination calendar are not
identical, the hierarchical structure of the source
calendar would be restructured. At first, one or both
of calendars need to be converted to a calendar(s)
with the greatest common time unit. An example is
converting P:(year, month, day) to P:( year, week,
day). Since the time units used in the two calendars
are not identical, the hierarchical structure of
P:(year, month, day) will be restructured. The
corresponding hierarchical structure of P:(year,
month, day) is H:(year, month, day) and that of P:(
year, week, day) is H:(year, week, day). The
restructuring process is presented below:
Step1: Here, the common time unit is “day”. It is
the lowest level of the both hierarchies. The domain
of the lowest level (a set of Cartesian products) of
the source hierarchy is transformed to a set of
integers. For example, {(2005, 1, 1), (2005, 1, 2), …,
(2005, 12, 31)} → {1, 2, …, 365}.
Step2: According to the relationship between the
time unit at the lowest level and the time unit at the
higher level, the integers are partitioned and
assigned to the time unit at the higher level. For
example, {1, 2, …, 365} → {(1, 6), (1, 7), (2, 1), (2,
2), …, (53, 6)}.
Step3: Step2 will be recursively executed to
build the whole hierarchical structure of destination
calendar.
4.2 Converting a Complete
Calendar to a Composite
Calendar
If the time units used in the source calendar and in
the destination calendar are not identical, the
hierarchical structure of the source calendar would
be first restructured. Then, an operation exclude is
used to exclude time intervals from the source
calendar. In addition, an operation union is used to
combine time intervals. The operations are defined
below:
exclude (I, C): Exclude the time interval I from
the calendar C.
union (I
1
, I
2
): Combine time intervals I
1
and I
2
.
For example, exclude (union (holidays,
weekends), P:(year, month, day)) → R:(year, month,
day).
CONVERTING TIME SERIES DATA FOR INFORMATION SYSTEMS INTEGRATION
291
4.3 Converting a Composite
Calendar to Another Composite
Calendar
To avoid loss of data in the conversion, the
corresponding complete calendar for the source
calendar will be utilized. This complete calendar
will be converted to the corresponding complete
calendar for the destination calendar. According to
the structure of the destination calendar, the time
intervals will be excluded from the complete
destination calendar by using the operation exclude.
An example is converting R:(year, month, day)
to R:(year, week, day). The converting process is
illustrated below:
Step1: The hierarchical structure of the source
calendar H:(year, month, day) will be converted to
H:(year, week, day).
Step2: The operation exclude is used to exclude
time intervals from the destination calendar
(complete).
exclude (union (holidays, weekends), P:(year,
week, day)) → R:(year, week, day).
5 CONCLUSION
In this paper, I proposed a systematic method that
enables effectively converting time-series data
appearing in enterprises. Time-series data is
modelled as an attribute that is associated with a
calendar. Therefore, this work focuses on converting
calendar systems. I presented a generalized
representing form, with which various complex
structures of calendar systems can be represented in
a consistent form. The converting processes and
operations are based on the representing form. The
conversion between different calendars is presented
in detail.
REFERENCES
Chandra, R., Segev, A. & Stonebraker, M., 1994.
Implementing Calendars and Temporal Rules in Next
Generation Databases. In Proc. 3rd Int’l Conf. On
Data Engineering, pp.264-273.
Dangelmaier, W. & Ketterer, 1995. Industrial
Manufacturing Management Data. ISO
TC184/SC4/WG8-P3.
Dreyer, W., Dittrich, A.K. & Schmidt, D., 1994. An
Object-Oriented Data Model for a Time Series
Management System. In Proc. 7th Int’l Working Conf.
On Scientific and Statistical Database Management,
pp.186-195.
Dreyer, W., Dittrich, A.K. & Schmidt, D., 1994. Research
Perspectives for Time Series Management Systems. In
ACM SIGMOD Record, Vol. 23, No. 1, pp.10-15.
Dreyer, W., Dittrich, A.K. & Schmidt, D., 1995. Using the
CALENDAR Time Series Management System. In
Proc. ACM SIGMOD Int’l Conf., pp.489-502.
Dyreson, C. E. & Snodgrass, R. T., 1993. Timestamp
Semantics and Representation. In Information
Systems, 18, No.3, pp.143-166.
Elmasri, R. & Wuu, G., 1990. A Temporal Model and
Query Language for ER Database. In IEEE Data
Engineering Conference.
Gadia, S. & Yeung, C., 1990. A Generalized Model for a
Temporal Relational Database. In ACM SIGMOD
Conference.
Lee, J. Y., Elmasri, R. & Won, J., 1996. Specification of
Calendars and Time Series for Temporal Databases. In
Conceptual Modeling – ER’96. pp.341-356.
Peng, L., 2001. Datenkonversion fuer den Datenaustausch
in verteilten Fertigungslenkungssystemen. HNI-
Verlagsschriftenreihe, Bd.98.
Rose, E. & Segev, A., 1991. TOODM – A Temporal
Object-Oriented Data Model with Temporal
Constraints. In Proc. 10th International Conference on
the Entity-Relationship Approach.
Snodgress, R., 1995. The TSQL2 Temporal Query
Language. Kluwer Academic Publisher.
2005
(2005, 1) (2005, 12)…
(2005, 1, 1), …, (2005, 1, 31), …, (2005, 12, 1), …, (2005, 12, 31)
Fi
g
ure 5: The hierarchical
d
omain of the Gre
g
orian calenda
r
.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
292
