DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS

BY A META-LEARNING APPROACH BASED ON GRAMMAR

EVOLUTION

Albert Fornells-Herrera, Elisabet Golobardes-Rib

e and Ester Bernad

o-Mansilla

Research Group in Intelligent Systems

Enginyeria i Arquitectura La Salle, Ramon Llull University. Quatre Camins 2, 08022 Barcelona (Spain)

Joan Mart

ı-Bonmat

Computer Vision and Robotics Group

University of Girona. Avda. Llu

ıs Santal

o s/n, 17071 Girona (Spain)

Keywords:

Breast Cancer Diagnosis, Strategic Decision Support Systems, Evolutionary Programming, Meta-Learning,

Application of Artiﬁcial Intelligence on Medicine.

Abstract:

The incidence of breast cancer varies greatly among countries, but statistics show that every year 720,000 new

cases will be diagnosed world-wide. However, a low percentage of women who suffer it can be detected using

mammography methods. Therefore, it is necessary to develop new strategies to detect its formation in early

stages. Many machine learning techniques have been applied in order to help doctors in the diagnosis decision

process, but its deﬁnition and application are complex, getting results which are not often the desired.

In this article we present an automatic way to build decision support systems by means of the combination

of several machine learning techniques using a Meta-learning approach based on Grammar Evolution (MGE).

We will study its application over different mammographic datasets to assess the improvement of the results.

1 INTRODUCTION

Breast cancer is the most common cancer among

western women and is the leading cause of cancer-

related death in women aged 15-54. Screening pro-

grams have proved to be good practical tools for pre-

maturely detecting and removing breast cancer, and

increasing the survival percentage in women (Win-

ﬁelds et al., 1994). In an attempt to improve early

detection, a number of Computer Aided Diagnosis

(CAD) techniques have been developed. There are

several approaches to CAD, but we focus on the breast

cancer diagnosis using mammographic images. A

mammographic image is processed in order to iden-

tify the microcalciﬁcations (µCa) that appear. Hu-

man experts agree on their relevance in diagnosing a

new case. After characterizing the µCa through a set

of features, we diagnose each image using machine

learning techniques. Previous studies applying ma-

chine learning techniques found that these techniques

improved the accuracy rate (in terms of correct clas-

siﬁcations) but decreased the reliability rate (in terms

of robustness and stability) compared to human ex-

perts (Golobardes et al., 2002). Our purpose is to

improve the reliability rate so experts can have more

conﬁdence in the results, when they need to decide

whether a sample is benign or malign.

When people make critical decisions, they usually

take into account the opinions of several experts rather

than relying on their own judgement or that of an only

trusted advisor. Therefore, an obvious approach for

making more reliable decisions is to combine the out-

put of several models/classiﬁers by means of a meta-

level, which coordinates the decision support system.

Although a 100% of reliability is not assured, the con-

ﬁdence in the results is usually increased.

However, models’ combination has the disadvan-

tage of being rather hard to design as it is not easy

to intuitively understand what factors are contribut-

ing to the different predictions. An automatic process

that searched for the best combination of single clas-

siﬁers would help in the design process. In this pa-

per, we propose an automatic way of deﬁning deci-

sion support systems using a Meta-learning approach

based on Grammar Evolution (MGE). Grammar Evo-

lution (GE) (Ryan et al., 1998) is a variant of Evolu-

tionary Computation (EC) (Goldberg, 1989) designed

to ﬁnd algorithms using a genotype to fenotype map-

ping process by means of a Backus Naur Form (BNF)

grammar, which leads the searching process. We

adapt a GE to guide the search to the most reliable

schema of classiﬁer combinations. Also, the result-

222

Fornells-Herrera A., Golobardes-Ribé E., Bernadó-Mansilla E. and Martí-Bonmatí J. (2006).

DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS BY A META-LEARNING APPROACH BASED ON GRAMMAR EVOLUTION.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 222-229

DOI: 10.5220/0002492202220229

 SciTePress

ing meta-learning approach will be applied to breast

cancer diagnosis.

This article is organized as follows. Section 2 sur-

veys some related work. Section 3 sets the back-

ground of classiﬁer combination, and deﬁnes the main

structure of our meta-learning approach (MGE). Sec-

tion 4 describes the particular setting of MGE for the

breast cancer diagnosis problem. Next, Section 5 an-

alyzes the results and ﬁnally, we summarize conclu-

sions and further work in section 6.

2 RELATED WORK

Several decision support systems have been applied

to perform the diagnosis of breast cancer using the

µCa extracted from mammographic images. Some

of them are Support Vector Machines (Campani

et al., 2000), Nearest-Neighbour algorithms (Kauff-

man et al., 2000), Bayesian Networks (Edwards et al.,

2000) or Fuzzy Neural Networks (Cheng et al., 1998).

We have been working successfully with different

Artiﬁcial Intelligence (AI) techniques such as Genetic

Algorithms (GA) (Goldberg, 1989) and Case Base

Reasoning (CBR) (Aamodt and Plaza, 1994) to tackle

this problem (Garrell et al., 1999) (Golobardes et al.,

2002). However, we prefer to focus in a CBR ap-

proach because it allows experts to get an explana-

tion of its classiﬁcation (malign or benign) in terms

of the most similar cases. In these previous works,

the results were compared with the classiﬁcations by

human experts (Mart

ı et al., 2000). The conclusions

were that AI techniques improved the accuracy rate

but the reliability rate was decreased. One of the rea-

sons was the difﬁculty of deﬁning a reliable similarity

function for CBR.

In (Golobardes et al., 2001) a Genetic Program-

ming (GP) (Koza, 1992) approach was used as an

automatic process for designing similarity functions

for CBR. The system found a similarity function that

improved the previous results, but they were still not

good enough. The reason was attributed to the huge

search space in which the GP had to ﬁnd the solu-

tion. In (Fornells et al., 2005b) a new approach based

on GE and CBR was proposed to reduce the search

space, by the use of a grammar that led the search

process. The comparison of the GP-CBR approach

and the GE-CBR approach showed that the GE-CBR

approach works better if the grammar is well deﬁned

(Fornells et al., 2005a).

Combining multiple models is a popular research

topic in machine learning research. The most im-

portant methods for combining models are bagging

(Breiman, 1996a), boosting (Schapire et al., 1997)

and stacking (Wolpert, 1990). Bagging and boosting

are based in the combination of their outputs using

voting schemes. The difference between them is that

boosting uses a weighting vote. On the other hand,

Stacking was introduced by Wolpert (Wolpert, 1990)

in the neural network literature, and it was applied to

numeric prediction by Breiman (Breiman, 1996b). It

is a technique based on a meta-level that makes deci-

sions using heuristics which combine the outputs of

several classiﬁers. Later, Ting and Witten (Ting and

Witten, 1997a) compared different meta-level mod-

els empirically and found that a simple linear model

performs best. Also, they demonstrated the advan-

tage of using the probabilities of classiﬁer predictions

as meta-level data. A combination of stacking and

bagging was also investigated in (Ting and Witten,

1997b). Many different models were generated by

varying the learning parameters (Oliver and Dowe,

1995) (Kwok and Carter, 1990) and by using differ-

ent sampling methods (Freund and Schapire, 1996)

(Ali and Pazzani, 1996).

In (Vallesp

ı et al., 2002) these concepts were used

to deﬁne several meta-levels by means of heuristics

based on the results of different machine learning

techniques over the mammography dataset proposed

in (Mart

ı et al., 2000). Nevertheless, this way of deﬁn-

ing meta-levels is very limited. For this reason, we

propose MGE as an automatic way of deﬁning meta-

levels, and we study its application over new and im-

proved datasets of breast cancer diagnosis.

3 MGE: META-LEARNING

APPROACH BASED ON

GRAMMAR EVOLUTION

3.1 Meta-learning

Meta-learning can be deﬁned as learning from infor-

mation generated by a(some) learner(s). It can also be

viewed as learning meta-knowledge from the learned

information. Therefore, it is a general technique to

coalesce the results of multiple classiﬁers.

It requires at least two levels: A level composed

by a set of trained classiﬁers (level-0 model) using a

subset of the original dataset (level-0 data), and an-

other level trained (level-1 model) using the outputs

of the level-0 models (level-1 data). (Breiman, 1996a)

demonstrated that the combination of all the model-0

outputs usually improves the results of the individual

classiﬁers.

Level-0 models can be of two types: (1) Heteroge-

neous (the classiﬁers used are different) and (2) Ho-

mogeneous (all the classiﬁers used are equal). In turn,

level-0 data can be distributed by each classiﬁer in

several ways: (1) Duplicating all the samples, (2) Dis-

tributing samples clustered in disjoint subsets, or (3)

DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS BY A META-LEARNING APPROACH

BASED ON GRAMMAR EVOLUTION

223

Distributing samples clustered in subsets allowing the

repetition of the samples. Breiman (Breiman, 1996a)

exposed that it is desired to level-0 models to be un-

stable, which means that they should be easily altered

if their training dataset is altered. Nevertheless, Ting

and Witten in (Ting and Witten, 1997b) demonstrated

that it is not necessary. However, they both agree

that the level-0 design process is critical in the sense

that all classiﬁers must complement each other, that

is, they need to cover all the possible solutions.

The ﬁrst difﬁculty in the level-1 design process is

to deﬁne what data from the output of level-0 clas-

siﬁers should be used: (1) Only the class predicted

(Breiman, 1996a), (2) The class predicted and the

most similar samples (Chan and Stolfo, 1993), or (3)

the probabilities of belonging to each possible class

(Ting and Witten, 1997a). Option (1) does not al-

low level-1 model to get any measure of the conﬁ-

dence on the whole prediction. Although option (2)

adds extra information using the internal information

of level-0 models, it is difﬁcult to integrate differ-

ent internal representations. On the other hand, op-

tion (3) provides level-1 model information on the

conﬁdence in all the class predictions, which can be

used to better evaluate the behaviour of the level-0

models. Nevertheless, the selection of the type of

information used as level-1 data is conditioned by

the level-1 model. There are several ways of im-

plementing the level-1, of which the most impor-

tant are: (1) Manual heuristics deﬁned by an expert,

(2) Voting schemas (Breiman, 1996a), (3) Weighting

voting schemas (Schapire et al., 1997), (4) Arbiter

strategy based on solving conﬂicts (Chan and Stolfo,

1993), (5) Lineal regressions schemes (Ting and Wit-

ten, 1997a) and (6) Inductive and explanation-based

learning (Flann and Dietterich, 1989).

We can see that meta-learning allows the deﬁnition

of a hierarchy, which can be used to model a decision

support system.

3.2 Grammar Evolution

GE (Ryan et al., 1998) is a technique based on Evo-

lutionary Computation (EC), where a BNF grammar

is used in a genotype to fenotype mapping process in

order to transform the individual (represented by an

array of bits) into an executable program or function.

The ﬁtness is assigned depending on the result of the

program.

The BNF grammar is composed by a tuple {N, T, P,

S}. N and T represent the set of non-terminals and ter-

minals respectively, S is the starting production, and

P deﬁnes the rules for each production of the non-

terminals. At the beginning of the mapping process,

each individual has a program represented by the non-

terminals of the starting production. The ﬁrst step

consists of clustering the bits of the individual in inte-

1th Model

.....

Level-0

Models

Level-1

Model

Level-0

Data

Level-1

Data

New Problem

Individual Predictions

Kth

Model

Combined Prediction

Figure 1: Evaluation of an individual in MGE.

gers of X bits called codons, where X depends on the

production with more rules. Next, the non-terminals

elements are iteratively replaced by the elements of

one rule of the same production, which is selected us-

ing the codons of the individuals by the equation:

new rule = modulus of

actual codon

number of rules

(1)

This process is repeated until all the elements of the

program are terminals, and therefore the program can

be run. If the codons have run out and the mapping

process has not ended, then a wrapping operator is

applied. It means that codons are reused again from

the beginning.

3.3 Deﬁnition of Meta-levels by

Means of GE

Subsection 3.1 describes the term meta-learning as

a system which learns from other learning systems.

Nevertheless, it is not trivial to deﬁne how to com-

bine the output of the level-0 models to get the level-1

model. For this reason, we want to automate it using

the GE approach, which needs the deﬁnition of the

BNF grammar and the evaluation of the individuals.

The BNF grammar can be deﬁned as an expression

that represents a linear regression, a set of rules, or

any way of combining the outputs of several level-0

models. This variety allows GE more ﬂexibility.

Figure 1 shows the evaluation of a sample by an in-

dividual (a potential meta-level), which consists of:

(1) Translation of the individual into an expression

modeled by the BNF grammar, (2) Test the sample

in all level-0 models in order to get the level-1 data,

(3) The last predictions are replaced in the expression

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

224

Table 1: Characteristics of the datasets studied.

Dataset Attr. Class Distribution

Wisconsin 10 benign (458), malign (241)

µCa 22 benign (121), malign (95)

DDSM 143 b1(61), b2(185), b3(157),

b4(98)

MIAS-Birads 153 b1(128), b2(78), b3(70),

b4(44)

MIAS-3C 153 fatty(106), dense(112),

glandular(104)

to get the combined prediction. Finally, the ﬁtness of

the individual is computed using the statistics over all

the tested samples.

4 SETTING MGE FOR THE

PROBLEM

4.1 Datasets

We applied our approach to different datasets re-

lated with breast cancer diagnosis (see Table 1).

The Wisconsin dataset comes from UCI repository

(Blake and Merz, 1998) and the rest of the them

belong to our own repository. These are mammo-

graphic images digitalized by the Computer Vision

and Robotics Group from the University of Girona.

The µCa dataset (Mart

ı et al., 2000) contains sam-

ples from Trueta Hospital (in Girona), while DDSM

(Heath et al., 2000) and MIAS (Suckling et al., 1994)

are public mammographic images datasets, which

have been studied and preprocessed in (Oliver et al.,

2005b) (Oliver et al., 2005a) respectively. The µCa

dataset contains samples of mammographies previ-

ously diagnosed by surgical biopsy, which can be be-

nign or malign. DDSM and MIAS-Bi classify mam-

mography densities, which was found relevant for the

automatic diagnosis of breast cancer. Experts clas-

sify them either in four classes (according to BIRADS

(Samuels, 1998) classiﬁcations) or three classes (clas-

siﬁcation used in Trueta Hospital).

4.2 Level-0 Model

As we mentioned previously, we focus in CBR be-

cause it provides an explanation of its classiﬁcation.

In order to select the most suitable level-0 mod-

els, a previous study testing several techniques is

needed over the different datasets. A self CBR ap-

proach with different conﬁgurations was tested with

different similarity functions (Clark, Cosines, Ham-

ming, Euclidean, Cubic) using sample correlation as

weighting schema, and three nearest neighbour tech-

nique in the retrieval phase. Other machine learn-

ing techniques from Weka (Witten and Frank., 2000)

were also tested: IBK (Aha and Kibler, 1991), ID3

(Quinlan, 1986), C4.5 (Quinlan, 1993), PART (Frank

and Witten, 1998), Bayesian Neural Network (BNN)

(Freeman and Skapura, 1991) and Sequential Mini-

mal Optimization (SMO) (Platt, 1998).

N={ <program>, <expression>, <prob>,

<op>, <constant> }

T={if, (, ), else, then, endif, ≥, <, class

,...,

class

,noclass, P

class

,...,P

class

}

S={<program> }

<expr.> ← if (<prob><op><constant>) then

else

endif

← class

| ...| class

| no class

<prob> ← P

class

| ...| P

class

<op> ←≥|<

<constant> ← 0.25 | 0.5 | 0.75

Figure 2: BNF grammar used in GE.

Table 2 summarizes the error rates and the standard

deviation for each dataset. The results were computed

using a 10-fold stratiﬁed cross-validation, and using

10 random seeds. Because we want to improve the

results for all datasets, the level-0 models selected are

these which have the lowest error and lowest standard

deviation. They are marked using bold letters.

4.3 Level-1 Model

As we explained in subsection 3.1, the most useful

level-1 data is the probability of belonging to each

possible class. In the CBR approach, it is computed

using the equation proposed by (Ting and Witten,

1997a):

x =



s=1

f(y

)/d(x, x

)



s=1

1/d(x, x

)

(2)

where:

x is the new problem to solve

is the case ’s’ retrieved

d(x, x

) is the difference between ’x’ and ’x

’

p indicates the number of samples returned

f(y

) is ’1’ if i = y

, and ’0’ otherwise

The probabilities for the other methods are com-

puted internally by Weka. We deﬁne the level-1

data as a list of predictions generated by the sam-

ples tested, where each prediction is composed by the

probabilities of belonging to each possible class (C),

for each level-0 model used.

DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS BY A META-LEARNING APPROACH

BASED ON GRAMMAR EVOLUTION

225

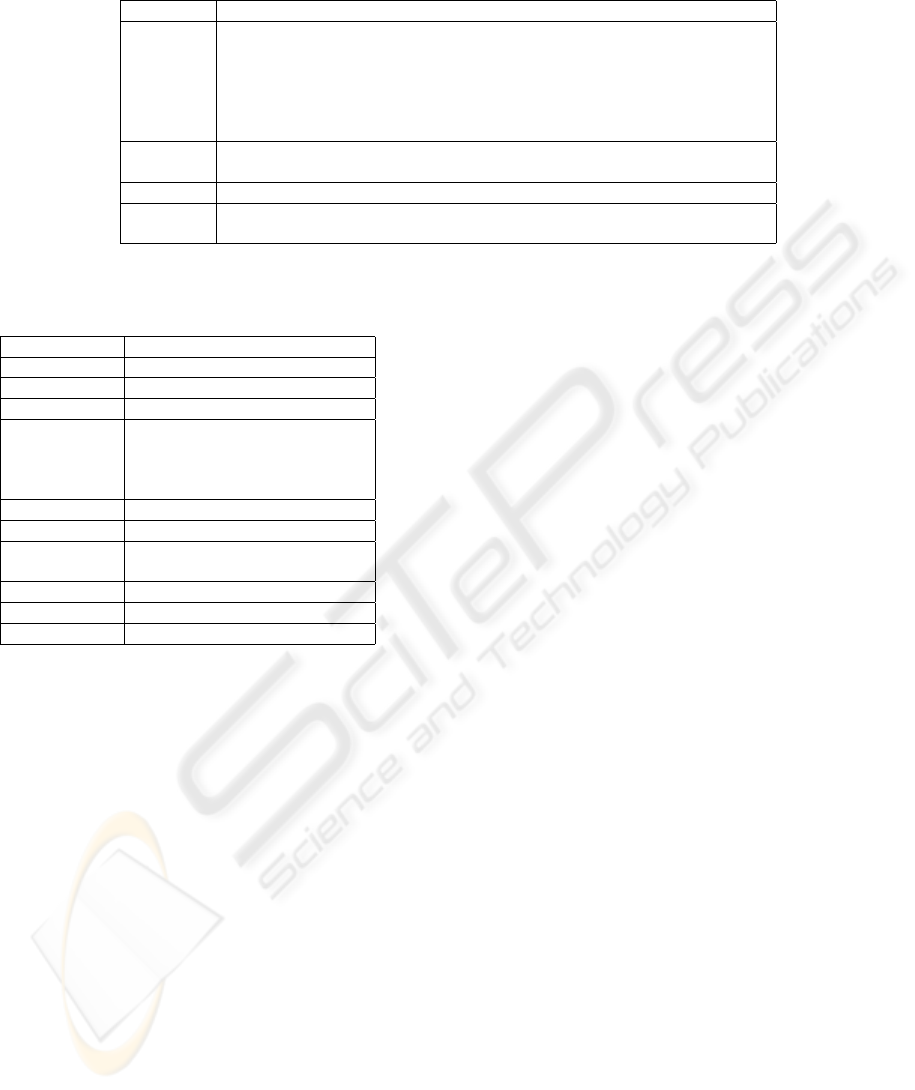
Table 2: % of error and standard deviation using several machine learning over the datasets of the table 1.

Method Wisconsin µCa DDSM MIAS-Bi MIAS-3C

Clark 10.80 (9.23) 34.26 (4.6) 44.71 (6.6) 26.88 (7.15) 22.61 (8.4)

Cosines 34.5 (1.4) 43.98 (9.4) 88.42 (6.74) 85.63 (7.2) 81.37 (9.2)

Hamming 3.43 (1.3) 32.41 (9.54) 55.09 (5.9) 33.13 (6.4) 32.30 (5.9)

Euclidean 3.42 (1.2) 34.72 (7.14) 53.49 (5.6) 29.69 (5.4) 29.19 (6.3)

Cubic 3.41(1.5) 33.38 (7.4) 52.30 (6.4) 32.81 (5.09) 31.06 (5.8)

(k=3) 3.43 (1.3) 30.55 (11.3) 53.29 (9.5) 29.69 (12.3) 27.63 (7.9)

ID3 5.86 (2.5) 35.65 (8.3) 45.70 (6.7) 29.06 (11.7) 32.06 (9.6)

C4.5 5.43 (1.9) 39.81 (10.2) 51.09 (3.5) 31.56 (11.5) 34.16 (8.7)

PART 5.29 (1.9) 38.42 (8.5) 55.88 (7.8) 42.51 (10.12) 34.78 (8.2)

BNN 4.01 (2.4) 36.11 (9.8) 56.48 (5.2) 32.81 (9.3) 29.51 (9.7)

SMO 3.43 (1.6) 31.48 (11.1) 44.11 (5.6) 29.68 (11.6) 25.15(5.2)

Table 3: GE conﬁguration.

Parameter Value

Generation 500

Population 1000

Ending 0.95% of the ideal ﬁtness

Operators Prob. Cross (0.8)

Prob. Repro. (0.2)

Prob. Mutation (0.3)

Max. Wrappring (2)

Selection Tournament (2)

# Codons 200 codons

Evaluation Eq. 3 with statistics from the

level-1 outputs

Initialization Ramped

Replacement Steady-State (SS)

Random Seed 10

Figure 2 represents the grammar that deﬁnes the

genotype to fenotype mapping process used to trans-

form the individual into a level-1 model. At the end of

the GE training process, the individual with the best

ﬁtness will be selected as the level-1 model.

The ﬁtness of individuals is computed by equation

3, which is based on the statistic about the accuracy

rate, and unclassiﬁed rate from the level-1 outputs:

fitness =0.75 · accuracy − 0.25 · unclassified (3)

Each component has an associated weighting value

that models the individual’s behaviour. Finally, ta-

ble 3 contains the GE conﬁguration used in the meta-

learning searching process.

4.4 Training and Testing the Models

Given a dataset α = {(y

),n =1..N}, where

is the class value and x

represents the attribute

values of the nth instance. The samples are randomly

split into J equal parts α

,...,α

. Let’s deﬁne α

test

and α

train

= α − α

test

to be the test and training

sets for the jth fold of a J-fold cross-validation. Also,

train

is split into M equal parts β

,...,β

. Let’s

deﬁne β

test

j,m

and β

train

j,m

= α

train

−β

test

j,m

to be the test

and training sets for the mth fold of another M-fold

cross-validation.

Training MGE consists of M training subcycles of

the level-0 models. Each one uses β

train

j,m

as level-0

data and β

test

j,m

to test the level-0 model. The proba-

bilities of belonging to each class are used as level-1

data for the MGE individual that is being evaluated to

obtain the statistics. The average of the M statistics

allows the system to compute the ﬁtness using equa-

tion 3. The MGE ﬁnal statistics are computed in a

J fold cross-validation, which implies training MGE

with α

train

and testing with α

test

J times.

It is obvious that this training and testing process

is computationally expensive as the evaluation of one

individual implies several runs of the level-0 mod-

els. Nevertheless, this penalization can be avoided if

all the predictions resulting from all β

train

j,m

and β

test

j,m

∀jin1 ...J ∀min1 ...M are previously computed.

Therefore, the individual’s evaluation only implies the

replacement of the precomputed predictions into the

expression, and running time is drastically decreased.

This way of training and testing the system war-

rants that test folds are independent, and the individ-

ual found by MGE is tested using samples that have

not been used in the training process.

5 RESULTS AND DISCUSSION

Tables 4, 5, 6, 7 and 8 show the error rate (percentage

of missclassiﬁcations) and the standard deviation for

the datasets of Table 1 using the experimental set de-

scribed in subsection 4.4. Also, we have applied Bag-

ging (Breiman, 1996a), AdaBoostM1 (Freund and

Schapire, 1996) and Stacking (Wolpert, 1990) from

Weka in order to compare their results.

The results can be analyzed from two points of

view: the improvement of meta-classiﬁers in compar-

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

226

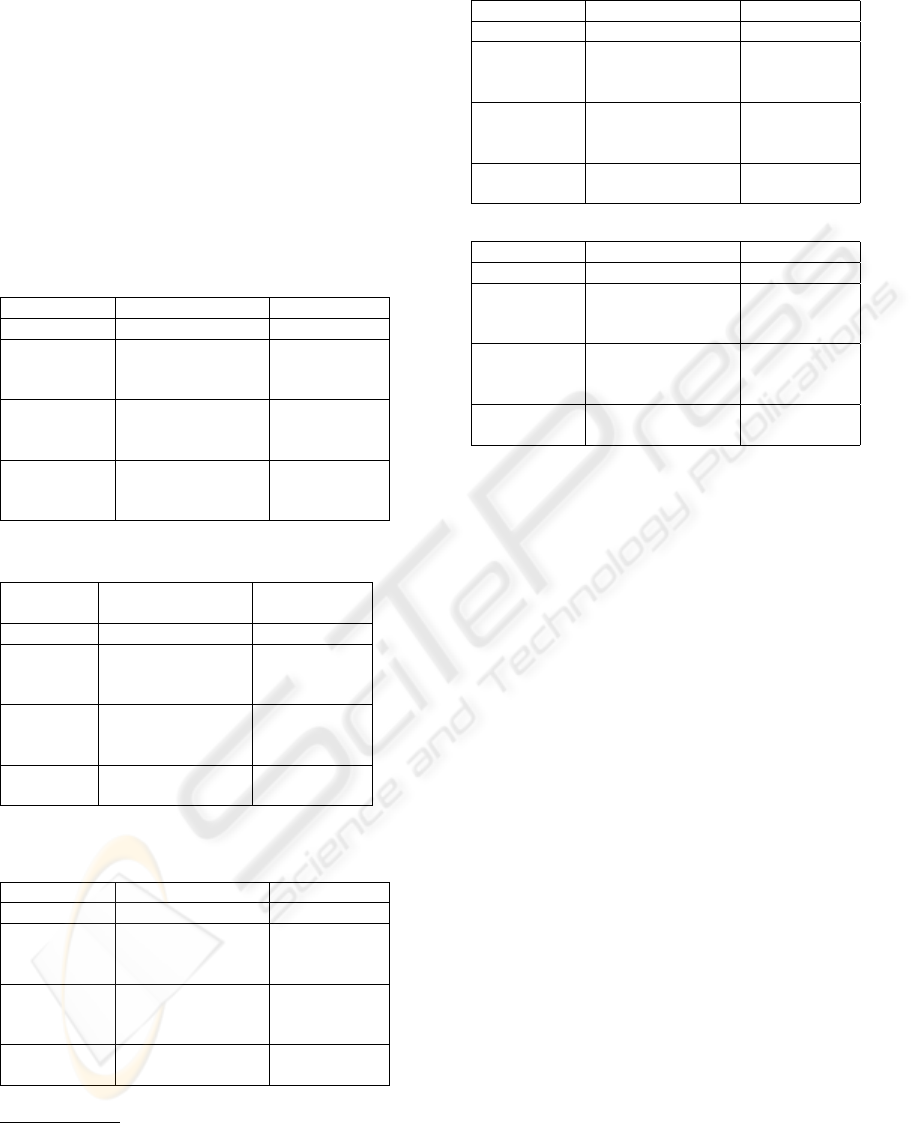
ison with the single classiﬁers, and the MGE improve-

ment with respect to the other meta-classiﬁers.

The results of a meta-classiﬁer are related with the

results of its level-0 models. Comparing tables 5 - 8

with table 2, we observe that the meta-classiﬁer ap-

proaches do not improve the error rate. Wisconsin

dataset is the exception because the MGE approach

(table 4) improves the results of the level-0 predic-

tions (table 2). This happens because this problem is

less complex than the others. Also, we have applied

a t-test student between the best single-classiﬁers and

the MGE results, and the improvements are not statis-

tical signiﬁcant (at 95% conﬁdence level)

Table 4: % of error and dev. in Wisconsin.

Meta-level Level-0 models Error

MGE Euc., Cub., SMO 2.72 (1.7)

Bagging Ib

3.43 (1.6)

Bagging BNN 4.01 (2.5)

Bagging SMO 3.43 (1.9)

AdaBoost Ib

3.14 (1.8)

AdaBoost BNN 4.86 (1.9)

AdaBoost SMO 3.43 (1.7)

Sta-Ib

, BNN, SMO 3.57 (1.7)

Sta-BNN Ib

, BNN, SMO 3.29 (1.4)

Sta-SMO Ib

, BNN, SMO 3.57 (1.5)

Table 5: % of error and dev. in µCa.

Meta-

level

Level-0 models Error

MGE Ham., IB3, SMO 32.33 (9.7)

Bagging Ib

33.79 (10.3)

Bagging ID3 35.68 (10.8)

Bagging SMO 33.33 (12.1)

AdaBoost Ib

33.79 (11.7)

AdaBoost ID3 36.11 (9.9)

AdaBoost SMO 32.48 (11.1)

Sta-Ib

, ID3, SMO 39.81 (11.2)

Sta-SMO Ib

, ID3, SMO 35.64 (10.5)

Table 6: % of error and dev. in DDSM.

Meta-level Level-0 models Error

MGE Clk., ID3, SMO 47.10 (5.6)

Bagging C4.5, 51.29 (4.5)

Bagging ID3 49.91 (6.4)

Bagging SMO 44.91 (6.3)

AdaBoost C4.5 53.89 (8.3)

AdaBoost ID3 46.31 (4.3)

AdaBoost SMO 42.72 (5.7)

Sta-C4.5 C4.5, ID3, SMO 46.31 (6.2)

Sta-SMO C4.5, ID3, SMO 50.49 (5.9)

Sta-XXX means that stacking is applied using XXX as

meta-classiﬁer. ID3 is not supported as meta-classiﬁer in

Weka tool because it only works with nominal values

The CBR approach is not supported in Weka tool. We

apply the next best level-0 model

Table 7: % of error and dev. in MIAS-Birads.

Meta-level Level-0 models Error

MGE Clk, Ib

, SMO 32.50 (10.6)

Bagging ID3 34.37 (10.8)

Bagging Ib

29.71 (11.9)

Bagging SMO 30.93 (12.8)

AdaBoost ID3 38.43 (5.9)

AdaBoost Ib

32.82 (11.2)

AdaBoost SMO 33.12 (11.6)

Sta-Ib

ID3, Ib

, SMO 40.93 (11.8)

Sta-SMO ID3, Ib

, SMO 33.43 (10.4)

Table 8: % of error and std. in MIAS-3C.

Meta-level Level-0 models Error

MGE Clk., ID3, SMO 28.57 (4.6)

Bagging Ib

30.12 (6.8)

Bagging ID3 30.74 (8.8)

Bagging SMO 23.91 (5.1)

AdaBoost Ib

29.81 (8.8)

AdaBoost ID3 38.19 (6.2)

AdaBoost SMO 26.31 (5.1)

Sta-Ib

ID3 SMO 33.85 (7.1)

Sta-SMO Ib

ID3 SMO 31.98 (6.3)

if ( P

< 0.75 ) then Class

else if (

≥ 0.25 ) then if (P

< 0.25 ) then Class

else Class

endif else Class

endif endif

Figure 3: Meta-level discovered in Wisconsin.

if ( P

≥ 0.75 ) then if ( P

≥ 0.50

) then Class

else unknown endif else if (

< 0.75 ) then Class

else if ( P

≥ 0.75

) then unknown else if ( P

v0.50 ) then Class

else Class

endif endif endif endif

Figure 4: Meta-level discovered in µCa.

if ( P

≥ 0.75 ) then Class

else if (

< 0.25 ) then Class

else if ( P

< 0.75

) then if ( P

≥ 0.75 ) then Class

else Class

endif else Class

endif endif endif

Figure 5: Meta-level discovered in DDSM.

if ( P

≥ 0.50 ) then Class

else if (

< 0.50 ) then if ( P

≥ 0.25 ) then Class

else if ( P

< 0.50 ) then if ( P

≥ 0.50 )

then Class

else Class

endif else unknown endif

endif else Class

endif endif

Figure 6: Meta-level discovered in MIAS-Birads.

if ( P

< 0.50 ) then if ( P

< 0.50

) then if ( P

< 0.25) then Class

else Class

endif else Class

endif

Figure 7: Meta-level discovered in MIAS-3C.

DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS BY A META-LEARNING APPROACH

BASED ON GRAMMAR EVOLUTION

227

On the other hand, the MGE results compared with

the other meta-algorithm results can be considered

good (although not statistically signiﬁcant) as MGE

almost always gets the lowest error, and the lowest

standard deviation. For these reasons, the MGE re-

sults can be considered a little robuster than the oth-

ers, and the MGE application provides the user more

conﬁdence on the results. The improvement of the

MGE results is related to the number of attributes of

the datasets. In Wisconsin and µCa datasets, the MGE

provides the best results, but in MIAS and DDSM

datasets they are similar to the other methods. As

a further work we could study if training GE for a

higher number of generations could improve our re-

sults with MIAS and DDSM datasets.

Finally, ﬁgures 3, 4, 5, 6 and 7 show the meta-levels

found by MGE. The code P

means the proba-

bility of belonging to the class X of the classiﬁer Y.

6 CONCLUSIONS AND FURTHER

WORK

Meta-learning can be seen as a black-box that learns

from outputs generated by other learners, in order

to make an improved prediction with a higher con-

ﬁdence level. One of the most difﬁcult tasks is the

design of this black-box. For this reason, we propose

MGE as an automatic way to deﬁne the relationships

between level-0 models. MGE uses the GE approach,

which is an EC approach based on a BNF grammar

that leads the search process.

We have tested MGE over different breast cancer

datasets and compared them with other meta-learning

classiﬁers. Although the t-test did not ﬁnd statistical

differences (at 95% conﬁdence level), MGE almost

always provided the lowest error and the lowest stan-

dard deviation. Therefore, MGE can be considered

robuster than the others. Another important feature of

MGE is that it can be easily tuned changing the BNF

grammar without modifying the program, in order to

set new ways of searching for relationships between

the level-0 models. Also, MGE is adaptable to the

datasets but Bagging, Adaboost and Stacking are not.

Therefore, MGE can be used as a decision support

system to help experts in breast cancer diagnosis to

reinforce their opinion about the type of sample they

are analizying.

Further work should deepen into the study of al-

ternative ways of evaluating individuals and how they

contribute to different level-0 models. Also other type

of grammars could lead to different combinations of

level-0 models. Adapting MGE to a distributed de-

cision support system using a multiagent approach

could beneﬁt cost and could potentially give better re-

sults. Finally, we plan to enhance the study to other

datasets.

ACKNOWLEDGEMENTS

The authors acknowledge the support provided under

grant numbers TIC2002-04160-C02-02, TIC2002-

04036-C05-03, TIN2005-08386-C05-04, 2005FIR

00237 and 2002 SGR-00/55. Also, we would like

to thank Enginyeria i Arquitectura La Salle of Ra-

mon Llull University for their support to our research

group.

REFERENCES

Aamodt, A. and Plaza, E. (1994). Case-based reasoning:

Foundations issues, methodological variations, and

system approaches. IA Communications, 7:39–59.

Aha, D. and Kibler, D. (1991). Instance-based learning al-

gorithms. Machine Learning, 6:37–66.

Ali, K. M. and Pazzani, M. J. (1996). Error reduc-

tion through learning multiple descriptions. Machine

Learning, 24(3):173–202.

Blake, C. and Merz, C. (1998). UCI repository of machine

learning databases.

Breiman, L. (1996a). Bagging predictors. Machine Learn-

ing, 24(2):123–140.

Breiman, L. (1996b). Stacked regression. Machine Learn-

ing, 24(1):49–64.

Campani, R., Bazzani, A., Bevilacqua, A., Bollini, D., and

Lanconelli, N. (2000). Automatic detection of clus-

tered microcalciﬁcations using combined method with

a support vector machine classiﬁer. Int. Workshop on

Digital Mammography.

Chan, P. K. and Stolfo, S. J. (1993). Experiments on mul-

tistrategy learning by meta-learning. In CIKM ’93:

Proceedings of the second international conference on

Information and knowledge management, pages 314–

323, New York, NY, USA. ACM Press.

Cheng, H., Lui, Y., and Freinanis, R. (1998). A novel

approach to microcalﬁciations detection using fuzzy

logic technique. IEEE Transaction on Medical Imag-

ing, pages 442–450.

Edwards, D., Kupinski, M., Nagel, R., Nishikawa, R., and

Papaioannou, J. (2000). Using a bayesian neural net-

work to optimally eliminate false-positive microcalci-

ﬁcations detection in a cad scheme. Int. Workshop on

Digital Mammography.

Flann, N. S. and Dietterich, T. G. (1989). A study

of explanation-based methods for inductive learning.

Machine Learning, 4(2):187–226.

Fornells, A., Camps, J., Golobardes, E., and Garrell, J.

(2005a). Comparison of strategies based on evolution-

ary computation for the design of similarity functions.

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

228

In Artiﬁcial Intelligence Research and Development,

pages 231–238. IOS Press.

Fornells, A., Camps, J., Golobardes, E., and Garrell, J.

(2005b). Incorporaci

on de conocimiento en forma

de restricciones sobre algoritmos evolutivos para la

usqueda de funciones de similitud. In IV Congreso

Espa

nol sobre Metaheur

ısticas, Algoritmos Evolu-

tivos y Bioinspirados, MAEB’2005, pages 397–404.

Thomson.

Frank, E. and Witten, I. H. (1998). Generating accurate

rule sets without global optimization. In ICML ’98:

Proceedings of the Fifteenth Int. Conference on Ma-

chine Learning, pages 144–151. Morgan Kaufmann

Publishers Inc.

Freeman, J. A. and Skapura, D. M. (1991). Neural Net-

works: Algorithms, Applications and Programming

Techniques. Addison Wesley.

Freund, Y. and Schapire, R. E. (1996). Experiments with a

new boosting algorithm. In International Conference

on Machine Learning, pages 148–156.

Garrell, J., Golobardes, E., Bernad

o, E., and Llor

a, X.

(1999). Automatic diagnosis with genetic algo-

rithms and case-based reasoning. AI in Engineering,

13(4):362–367.

Goldberg, D. E. (1989). Genetic Algorithm in Search, Op-

timization, and Machine Learning. Addison-Wesley.

Golobardes, E., Llor

a, X., Salam

o, M., and Mart

ı, J. (2002).

Computer aided diagnosis with case-based reasoning

and genetic algorithms. Journal of Knowlegde Based

Systems, pages 45–52.

Golobardes, E., Nieto, M., Salam

o, M., J.Camps, Calzada,

G., Mart

ı, J., and Vernet, D. (2001). Generaci

o de fun-

cions de similitud mitjanc¸ant la programaci

o gen

etica

pel raonament basat en casos. CCIA, 25:100–107.

Heath, M., Bowyer, K., Kopans, D., Moore, R., and

Kegelmeyer, P. (2000). The digital database for

screening mammography. Int. Workshop on Dig.

Mammography.

Kauffman, G., Salﬁty, M., Granitto, P., and Ceccato, H.

(2000). Automated detection and classiﬁcation of

clustered microcalciﬁcations using morphological ﬁl-

tering and statistical techniques. International Work-

shop on Digital Mammography.

Koza, J. R. (1992). Genetic Programming. Programing of

computers by means of natural selection. MIT Press.

Kwok, S. W. and Carter, C. (1990). Multiple decision trees.

In UAI ’88: Proceedings of the Fourth Annual Con-

ference on Uncertainty in Artiﬁcial Intelligence, pages

327–338. North-Holland.

Mart

ı, J., Espa

nol, J., Golobardes, E., Freixenet, J., Garc

ıa,

R., and Salam

o, M. (2000). Classiﬁcation of microcal-

ciﬁcations in digital mammograms using case-based

reasonig. Int. Workshop on Digital Mammography.

Oliver, A., Freixenet, J., Bosch, A., Raba, D., and Zwigge-

laar, R. (2005a). Automatic classiﬁcation of breast tis-

sue. Iberian Conference on Pattern Recognition and

Image Analysis, pages 431–438.

Oliver, A., Freixenet, J., and Zwiggelaar, R. (2005b). Au-

tomatic classiﬁcation of breast density. IEEE Interna-

tional Conference on Image Processing. to appear.

Oliver, J. J. and Dowe, D. L. (1995). On pruning and averag-

ing decision trees. In Proceedings 12th Int. Conf. Ma-

chine Learning, pages 430–437. Morgan Kaufmann.

Platt, J. (1998). Fast training of support vector machine us-

ing sequential minimal optimizations. In Sch

olkipf,

B., Burges, C., and Smola, A., editors, Advances

in Kernel Methods-Support Vector Learning, Cam-

bridge, M.A. MIT PRess.

Quinlan, J. R. (1986). Induction of decision trees. Mach.

Learn., 1(1):81–106.

Quinlan, R. (1993). C4.5: Programs for Machine Learning.

Morgan Kaufmann Publishers.

Ryan, C., Collins, J. J., and O’Neill, M. (1998). Gram-

matical evolution: Evolving programs for an arbitrary

language. In Proceedings of the First European Work-

shop on Genetic Programming, volume 1391, pages

83–95. Springer-Verlag.

Samuels, T. H. (1998). Illustrated Breast Imaging Report-

ing and Data System BIRADS. American College of

Radiology Publications, 3rd edition.

Schapire, R. E., Freund, Y., Bartlett, P., and Lee, W. S.

(1997). Boosting the margin: a new explanation for

the effectiveness of voting methods. In Proc. 14th In-

ternational Conference on Machine Learning, pages

322–330. Morgan Kaufmann.

Suckling, J., Parker, J., and Dance, D. (1994). The mammo-

graphic image analysis society digital mammogram

database. In Gale, A., editor, Proc. 2nd Internat.

Workshop on Digital Mammography, pages 211–221.

Ting, K. M. and Witten, I. H. (1997a). Stacked generaliza-

tions: When does it work? In IJCAI, pages 866–873.

Ting, K. M. and Witten, I. H. (1997b). Stacking bagged and

dagged models. In Proc. 14th Int. Conference on Ma-

chine Learning, pages 367–375. Morgan Kaufmann.

Vallesp

ı, C., Golobardes, E., and Mart

ı, J. (2002). Im-

proving reliability in classiﬁcation of microcalciﬁca-

tions in digital mammograms using case-based rea-

soning. In Proceedings of the 5th Catalonian Confer-

ence on AI: Topics in Artiﬁcial Intelligence, Lecture

Notes In Computer Science, volume 2504, pages 101–

112, London, UK. Springer-Verlag.

Winﬁelds, D., Silbiger, M., and Brown, G. (1994). Tech-

nology transfer in digital mamography. Report of the

Joint National Cancer Institute, Workshop of May 19-

20, Invest. Radiol, pages 507–515.

Witten, I. H. and Frank., E. (2000). DataMining: Practi-

cal machine learning tools and techniques with Java

implementations. Morgan Kaufmann Publishers.

Wolpert, D. H. (1990). Stacked generalization. Technical

Report LA-UR-90-3460, The Santa Fe Institute, New

Mexic.

DECISION SUPPORT SYSTEM FOR BREAST CANCER DIAGNOSIS BY A META-LEARNING APPROACH

BASED ON GRAMMAR EVOLUTION

229