DYNAMIC SERVICE COMPOSITION:

A PETRI-NET BASED APPROACH

Michael K

ohler, Daniel Moldt, Jan Ortmann

University of Hamburg, Computer Science Department

Vogt-K

olln-Str. 30, D-22527 Hamburg

Keywords:

Web Services, High-level Petri Nets, Semantic Service Composition, Ontologies.

Abstract:

Dynamic service composition requires a formal description of the services such that an agent can process

these descriptions and reason about them. The amount of detail needed for an agent to grasp the meaning of a

service may lead to clumsy speciﬁcation.

Petri nets offer a visual modeling technique for processes, that offers a reﬁnement mechanism. Through this,

a speciﬁcation can be inspected on the level of detail needed for a given objective.

In this paper we introduce a Petri net based approach to capture the semantics of services by combining Petri

nets ideas from the description logic area focusing on ontologies. The resulting framework can than be used

by agents to plan about activities involving services.

1 INTRODUCTION

The dynamic composition of services requires a de-

tailed understanding of the effects the invocation of a

particular service has. This makes it necessary to have

a formal semantics that can be interpreted by machi-

nes.

There is always a tradeoff between formal and pre-

cise semantics of a model and ease of modeling. As-

suming that a semantic description always has to be

formal, we chose Petri nets as a conceptual back-

ground, which is rather intuitive because of its visual

notation and the possibility to reﬁne models. We con-

sider three aspects of semantic service modeling of

major importance:

• A common vocabulary shared by the participants

provided by a common ontology,

• a description of the functional behavior of single

Web services or parts thereof, and

• a description of the coordination of multiple ser-

vices.

An agent has some knowledge about the state of the

world it is located in. To change this state the (soft-

ware) agent can communicate to the world via mes-

sage passing (i.e. through the invocation of other ser-

vices). These messages have to be understood by

both sides which is guaranteed by a common onto-

logy. (For further information see (Staab and Studer,

2004).) The functional behavior will be described by

the change of the interpretation of an algebraic speci-

ﬁcation. This is related to ideas of abstract state ma-

chines (B

orger and St

ark, 2003). Finally the coordi-

nation and sequence in which the services are execu-

ted are modeled by a Petri net.

The combination of services has different aspects.

The services need to be invoked in the right order

and the right services showing the right behavior need

to be invoked. In this paper we will focus on the

operational aspects of behavior and will refer to e.g.

(van der Aalst, 2003) or (Kindler et al., 2000) for

an discussion of when services and workﬂows ﬁt to-

gether.

A Web service interprets the messages according to

a given ontology. Here, we make use of Description

Logics (Baader et al., 2002) as the formal basis for

the ontology. To specify the functionality of a service,

we use algebraic constructs (Ehrig and Mahr, 1985).

By the execution of the different possible processes

of a net, an agent can then pick a sequence of services

best suited for a given objective. Planning can thus

be considered as reaching a particular marking from a

given one and is hence closely related to the planning

as model checking approach as e.g. in (Giunchiglia

and Traverso, 1999).

The paper starts with an example we will use to il-

lustrate the main idea in Section 2. Hereafter follows

a brief introduction to Description Logics in Section 3

before we introduce Service Description Nets in Sec-

tion 4. We will then illustrate the idea with the exam-

159

Köhler M., Moldt D. and Ortmann J. (2006).

DYNAMIC SERVICE COMPOSITION: A PETRI-NET BASED APPROACH.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - SAIC, pages 159-165

DOI: 10.5220/0002494901590165

 SciTePress

ple and give a short overview of our implementation

in Section 5 and will ﬁnally draw a conclusion and

give an outlook in Section 6.

2 MOTIVATIONAL EXAMPLE

Dynamic Web service orchestration is useful in a va-

riety of different application areas. Here, we will fo-

cus on the management of ship-supplies as an illustra-

ting example. Imagine a ship entering different ports

all over the world. The only time when it can purchase

supplies is while mooring in a port, which is normally

only a short period of time. Hence the delivery of all

supplies needs to be coordinated in advance such that

there is no delay. There might be different providers

offering different prices for the same goods. Additio-

nally we might have unexpected needs. For example,

due to heavy weather nobody attended the restaurant,

so that there is less need of food, but the weather cau-

sed a fuel shortage.

If we access the different providers of goods by

Web services, we would certainly like to know, what

happens if we chose a particular provider. This is

commonly given by a textual description which can-

not be understood by a machine. Thus we need a more

formal description of what happens. In the case of

ship supplies we have hard constraints such as the de-

livery time and we have things we would like to be

maximized or minimized such as quality and price.

What we need to know of a service is therefore what

effects it has on the particular part of the world that

we are interested in. Having a representation of the

world, we would like to know, how this representa-

tion changes. To allow a communication in general,

all parties involved need to comply with a common

vocabulary given by an ontology.

Different services can be classiﬁed based on there

behavior. If two providers offer the same item at dif-

ferent prices we will normally put them in the same

category of services. This can be reﬂected by a clas-

siﬁcation of services in a process ontology. The cal-

ling agent accesses a discovery service with a pro-

cess ontology to retrieve a list of services matching a

certain class. Through their semantic description the

agent can now determine, which of the services suits

its needs best.

3 ONTOLOGIES AND

DESCRIPTION LOGICS

Ontologies specify the concepts that are used in a gi-

ven domain. A concept is determined by its attributes

and by the roles existing between itself and the other

concepts. Concept descriptions are built inductively

from a set of primitive concepts, roles and attribu-

tes by using concept and role constructors. The most

widespread approach is to model the concepts of an

ontology by a Description Logic (DL). Different De-

scription Logics vary in their expressiveness, i.e. in

the number and kind of constructors they provide. We

distinguish between attributes as functional roles and

roles (non-functional). An example of a concept des-

cription would be the deﬁnition of a concept

LibraryBook

= Book ∀signature.Signature 

∀subject.String

Description logics knowledge bases are divided

into TBoxes and ABoxes. (For an in-depth discussion

on DL see (Baader et al., 2002).)

TBoxes (terminology boxes) hold intensional

knowledge in form of a terminology. They are built

through declarations of general properties of concepts

and thus restrict the set of possible worlds. More for-

mally, given a DL L,aL-TBox T is a ﬁnite set of

concept deﬁnition axioms of the form A

= C , with

A being a concept symbol and C being a L-concept

description (the deﬁning concept).

ABoxes (assertion boxes) on the other hand allow

to describe a speciﬁc state of the world. They hold

extensional knowledge that is speciﬁc to the individu-

als of the domain of discourse. A concept assertion is

denoted C(i) where C is a concept description and i

is an individual. A role assertion is denoted R(i

)

where R is a role symbol and i

are individuals.

An ABox A is a ﬁnite set of concept and role asserti-

ons. ABoxes are deﬁned with respect to some TBox.

The LibraryBook example above would be part of the

TBox T whereas the instance LibraryBook(book43)

would be part of an ABox wrt. T .

An interpretation I is a pair (∆

, ·

) consisting of

a domain ∆

= ∅ and an interpretation function ·

that assigns a set A

⊆ ∆

to every concept symbol

A, a partial function a

:∆

→ ∆

to every attri-

bute symbol a, and a binary relation R

⊆ ∆

× ∆

to every role symbol R.

Let C and D be concept descriptions. D subsumes

C, denoted as C  D,iffC

⊆ D

for all interpre-

tations I. C ≡ D ⇔ C  D ∧ C  D denotes the

equivalence of two concept descriptions.

4 MODELING OF SERVICE

BEHAVIOR USING NETS

To model scenarios like the one given in Section 2

we introduce Service Description nets. They have

been discussed more formally in (K

ohler and Ort-

mann, 2005). Service Description nets (SD nets) can

be mapped to algebraic Petri nets. This allows us

to adopt the analysis techniques introduced for them

ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING

160

order1

[]

Start

_order

End

_order

_err

_deliv

_acc

_order

_price

_acc

DeliveryReceipt

_err

_order

_err

_dr

Failure

guard _deliv

_order

FuelOrder

AccountInformation

acc1

_dr

order: FuelOrder

fail: Failure

price: Price

cancel:

return: DeliveryReceipt

Communication Channel

(place fusion)

Calling Agent

assign _acc = _customer.account;

assign (_customer) =

getCustomer(_login.name, _login.pw);

account: AccountInformation

FuelBuyService

FuelOrder

_deliv

_acc

assign _dr = new DeliveryReceipt;

assign _date = deliveryDate(_order.isbn);

set _dr.deliveryDate = _date;

set _dr.order = _order;

set _dr.price = _price;

FuelOrder

_order

_dr

_acc

_dr

assign (_deliv) = isDeliverable(_order.quantity);

_customer

Price

_login

assign _price = new Price;

update (_price.currency, _price.amount)

= priceLookup(_order.quantity);

_price

assign (_diff) = convertCurrency(

_price.amount,_price.currency,

_acc.currency);

update _acc.balance =

_bal => _bal-_diff;

_cc

_price

_cc

Price

_price

guard !_deliv;

assign _err =

new NotDeliverableFailure;

set _err.order = _order;

noop

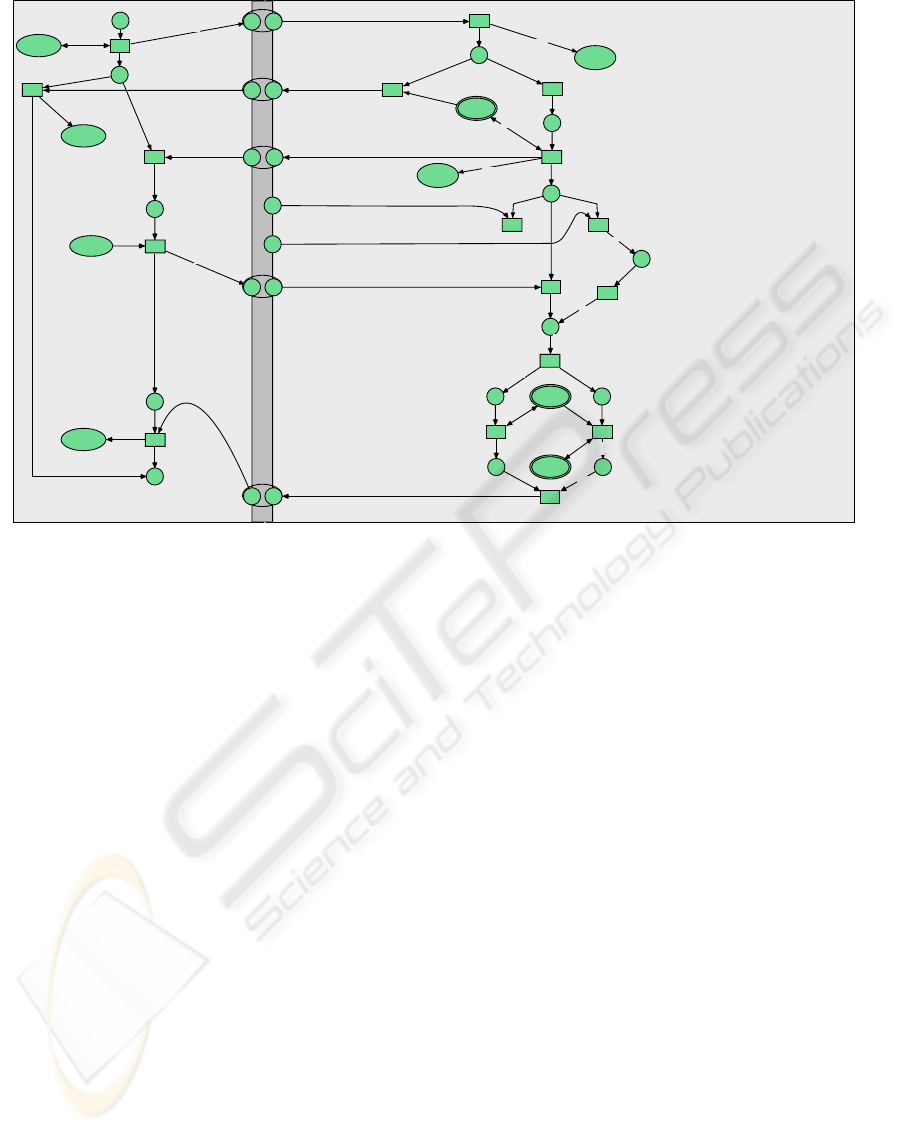
Figure 4.1: An Example for a Service Description Net.

(Reisig, 1991).

A Petri net is a bipartite graph consisting of places

and transitions. More formally a Petri net N is a triple

N =(P, T, F), where P is a ﬁnite set of places, T is

a ﬁnite set of transitions with P ∩ T = ∅, and F ⊆

(P × T ) ∪ (T × P ) is a ﬂow relation (a set of arcs).

The basic idea behind Service Description nets is

that each service affects the current state of the agents

world by changing the value of data items. A service

can either create new data items or it can modify the

attributes of existing data items. The data items are re-

presented by an ontology, which is based on Descrip-

tion Logics. Description Logics allows us to deﬁne

concepts on a formal basis and is on the other hand

well supported by tools. As described in Section 5 we

integrated (P

ROT

E, 2005, ) in our Petri net simu-

lation engine (R

ENEW, 2005, ) to have an executable

model.

SD nets allow us to model the workﬂow of a Web

service together with the data exchanged and manipu-

lated. Hence we make use of workﬂow nets (van der

Aalst, 2003) or more speciﬁcally of open workﬂow

nets (Reisig et al., 2005). Workﬂow nets reﬂect the

speciﬁc structure of workﬂows with a single starting

point and a single end point. Open Workﬂow nets

additionally introduce border places to model the in-

coming and outgoing messages of workﬂows. We

further extend the expressiveness by allowing typed

messages and by allowing the functional description

of activities. The types are taken from an ontology.

The concepts modeled in the ontology can be used in

the net. The roles and attributes modeled in the onto-

logy are hidden in the inscriptions. E.g. C.x refers to

the attribute x of a concept C.

To represent the concepts and the operations de-

ﬁned on them, we use order-sorted algebra (Go-

guen and Meseguer, 1992). Order-sorted algebra ex-

tends many-sorted algebras by a partial order relation,

which the sorts need to obey. Here, it is used to deﬁne

an order-sorted logical speciﬁcation as follows:

Deﬁnition 1 (Logical Speciﬁcation, Structure). A

logical speciﬁcation is a tuple LS =(S, ≤, Ω,E,Π)

where S is a set of sorts, ≤ is a partial order on the

set of sorts, Ω is a set of operation symbols and E is

a set of equations such that (S, ≤, Ω,E) is an order-

sorted speciﬁcation and Π=(Π

)

w∈S

∗

is a family

of predicate symbols, which is disjoint from S and Ω.

A structure (or interpretation) of a logical speci-

ﬁcation LS is a triple A

=(S

, Ω

, Π

) con-

sisting of a family of sets S

=(A

)

s∈S

respec-

ting ≤ and of operations Ω

=(ω

)

ω∈Ω

with ω

× ... × A

→ A

for all ω ∈ Ω

...s

well as a family of relations Π

=(π

)

π∈Π

with

⊆ A

× ...× A

for π ∈ Π

...s

. ♦

DYNAMIC SERVICE COMPOSITION: A PETRI-NET BASED APPROACH

161

Using a logical speciﬁcation we can now deﬁne the

current state of an agent’s world as formula in ﬁrst

order logic. This represents the ABox of our ontology.

To state, that ship vessel01 has 2000 gallons of fuel

we might have the following fact in our knowledge

base:

stored(vessel01,item04)∧ItemQuantity(item04)∧

quantity(item04,2000)∧unit(item04,Gallon)∧

type(item04,Diesel)

Naturally the knowledge base entry depends on the

ontology. Here, the predicates represent the roles (and

attributes) deﬁned by an ontology. The operations

deﬁned on the data are speciﬁed by an algebra. Fi-

gure 4.1 shows a potential description of a ship sup-

plies workﬂow as SD-net. Its underlying structure

consists of two open workﬂows that yield a workﬂow

net when composed by place fusion. The net on the

left side represents the calling client whereas the net

on the right side represents the Web service invoked.

Some information is optional to invoke FuelBuySer-

vice. The invoking service can either cancel the ope-

ration, provide a Login or some new AccountInforma-

tion. In Figure 4.1 the latter alternative is chosen.

We say a logical speciﬁcation is compatible with

an ontology if each named concept has a correspon-

ding sort, that respects the hierarchy deﬁned by the

ontology and each role has a least sort that is its do-

main among the set of sorts. Furthermore we require

the predicate symbols to have the sorts of the corre-

sponding roles. Through this, we can now deﬁne a

net class changing the current concepts and attributes

of an ontology by changing the interpretation of its

logical speciﬁcation, which we will call Service De-

scription Nets. These nets have special inscriptions

to change the interpretation of the predicates. Addi-

tionally we have variable assignments that assign the

result of a term evaluation to a variable, so that we can

create new items or use local variables.

We can now specify the syntax of the transition ins-

criptions. In the following we will let T

Σ,s

(X) denote

the set of terms of sort s over the set of variables X

wrt. the signature Σ.

Deﬁnition 2 (Assignment and Update, Consistency).

Let LS =(S, ≤, Ω,E,Π) be a logical speciﬁcation

and X a set of variables. Given v ∈ X

and s, s



∈ S

a variable assignment is of the form

1. assign v =news,

2. assign v = t



with t



∈ T

Σ,s

(X),or

3. assign v = t



.π with t



∈ T

Σ,s



(X), π ∈ Π



A predicate update for some π ∈ Π



, t ∈ T

Σ,s



(X)

is of the form

4. update t.π = t



with t



∈ T

Σ,s

(X).

A set of variable assignments Ass (Assignment set)is

consistent if no left hand side occurs more than once

in Ass, i.e. (assign v = rexp) ∈ Ass and (assign v =

rexp



) ∈ Ass implies rexp = rexp



. A set of pre-

dicate updates is consistent similarly if no left hand

side occurs more than once in it. A set of assignments

together with a set of updates is called a set of ac-

tion statements Act or Act(X) respectively if it ran-

ges over a speciﬁc set of variables X. ♦

If a variable occurs on the left hand side of a varia-

ble assignment it is called bound, otherwise it is called

free. The set of all bound variables of an assignment

set Ass is denoted by Bound(Ass).

The assignment statements deﬁne a natural exten-

sion α

ext

of a variable assignment α as long as there

are no circular dependencies in the assignment state-

ments. Each free variable gets assigned the value of

the term on the right hand side of the equation eva-

luated under ¯α or under the extended evaluation ¯α

ext

The ﬁring of a set of action statements is done by ﬁrst

evaluating the extended assignment, i.e. by evaluating

all assign statements, and then executing the update

statements.

Deﬁnition 3 (Firing of Action Statements). Given

an interpretation A

=(S

, Ω

, Π

) of LS and an

assignment α : X → A, where X is the set of all free

variables. The ﬁring of a set of action statements Act

ﬁrst evaluates all assignments yielding an extended

assignment α

ext

. Then the updates of the form u =

(update t

.π = t



) are evaluated in A

. This yields a

successor interpretation A



=(S

, Ω

, Π



) such

that we have Π



=(Π

\{π

}) ∪{π



} where



=(π

\{(¯α

ext

(t),x)}) ∪{(¯α

ext

(t), ¯α

ext



))}

for some value x. ♦

In a consistent update set, each predicate update af-

fects either a different predicate or a different value of

the same predicate. Therefore we have the following

lemma.

Lemma 4: For a consistent set of predicate updates

the ﬁring can be done in arbitrary order.

This allows us to speak of the ﬁring of a consistent

update set in an interpretation A

which will lead to

a successor interpretation. Now that we have modeled

the change of attributes and roles by logical speciﬁca-

tion and the creation of objects by assignments, we

can use this in a net, where we can deﬁne the order in

which these changes occur.

Service Description Nets (SD Net) consist of typed

places, arcs inscribed by variables and transitions with

guards. Additionally transitions specify the change

of the predicates. The control ﬂow is modeled by a

dedicated sort called s

token

which has the constant •

as its only operation symbol. If an arc or place has

no inscription it is implied that it is of sort s

token

Figure 4.1 shows an SD Net.

Deﬁnition 5 (Service Description Net, Service Des-

cription Net system). Let LS =(S, ≤, Ω,E,Π) be

ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING

162

a logical speciﬁcation compatible to an ontology O

such that LS contains the concrete domain B of boo-

leans as well as a sort ⊥

undef

, with ⊥⊥

undef

 C

for all C =⊥.

A Service Description Net is a tuple SDN =

def

(LS,X,N ,d,W,G,act) where

• LS =(S, ≤, Ω,E,Π) is a logical speciﬁcation

as deﬁned in Def. 4,

• X is a set of LS-variables,

•N=(P, T, F ) is a Petri net,

• d : P → S is a place typing,

• W : F → X is an arc inscription such that for

p ∈ P and f ∈ F we have W (f) ∈ (X

Bound(act(t))) with d(p) ≤ s if f =(p, t) and

W (f ) ∈ X

with s ≤ d(p) if f =(t, p),

• G : T → T

Σ,Bool

(X) assigns an enabling con-

dition to each transition, and

• act : T → Act(X) assigns a regular and consis-

tent set of assignments and updates to each tran-

sition as deﬁned in Def. 4.

A Service Description Net together with an initial

state Q

=(m

, I

) consisting of an initial mar-

king m

: P → T

such that for m

(p) ∈ T

Σ,s

have s ≤ d(p) for all p ∈ P and an initial interpreta-

tion I

=(S

, Ω

, Π

) of LS =(S, ≤, Ω,E,Π)

is called a Service Description Net system. ♦

To guarantee the executability of Service Descrip-

tion Nets, we require that a variable used on an output

arc of a transition is either also used on an input arc

or deﬁned through an assignment, thus reducing the

search space for possible bindings.

Deﬁnition 6 (State, Marking, Enabling and Firing).

A marking m of a Service Description Net SDN is

a mapping m : P → T

such that m(p) ∈ T

Σ,s

with s ≤ d(p) for p ∈ P .Astate Q =(m, I

)

is a marking together with an interpretation I

, Ω

, Π

) of LS.

A transition t is enabled under a variable assi-

gnment α : X → A iff the evaluation of the activation

condition ¯α(G(t)) = true and for all places p ∈ P

we have m(p) ≥ ¯α(W (p, t)) and α assigns a value to

each free variable in act(t).

The ﬁring of a transition under a variable binding

α is denoted as state transition Q

t,α

−−→ Q



which

is again split into m

t,α

−−→ m



and I

t,α

−−→I



is deﬁned for each place p ∈ P as m



(p)=

m(p) − α(W (p, t)) + α(W (t, p)). The interpreta-

tion I



=(S

, Ω

, Π



) is deﬁned as in Deﬁni-

tion 4 by successively applying the predicate upda-

tes (update t

.π = t



) ∈ act(t) resulting in a sequence

=Π

,...,Π

=Π



with Π

i+1

=(Π

\{π

}) ∪

{(π

\{(¯α(t),x)}) ∪{(¯α(t), ¯α(t



))}} for some value

x. ♦

For convenience reasons we introduce two abbre-

viating notions for Service Description Net inscripti-

ons:

5. update t

.π = v



⇒ t



, which is equivalent to the

assignment assign v



= t



.π together with the predi-

cate update update t

.π = t



, and

6. t

.π within a term expression, which is equivalent

to assign v



= t



.π and the usage of v



instead.

The second abbreviation allows us to write e.g.

assign v =

book.author.name instead of

assign v1 =

book.author and assign v = v1.name

Additionally we require a repository containing a sub-

set of A where assignments of the form (assign v =

new s) can retrieve an a ∈ A

that has not been pre-

viously used in the net. Practically this is done by a

pool, from which an element is taken. For most prac-

tical scenarios we have a ﬁnite set of items, so that we

can determine an upper bound as the size of the pool.

Furthermore it is often convenient in practice to

have not only binary relations but relations of arbi-

trary arity. Here, we will only consider functional re-

lations and call them predicates as well. For an n-ary

predicate π we additionally introduce

assign (v

,...,v

) = π(t

,...,t

), (i + j = n)

which replaces the value of v

,...,v

by appropriate

values such that (t

,...,t

) ∈ π

Through this, we can express database queries or

external queries that assign values to more than one

variable. In Figure 4.1 such an assignment operation

would be priceLookup. For these assignments the

deﬁnition of the logical speciﬁcation has to be modi-

ﬁed, to allow n-ary predicates.

There are some specialties about the net deﬁnition

above. We allow only one concept instance on each

place. Having more than one concept instance on a

single place results in picking one instance nonde-

terministicly, if more than one instance satisﬁes the

guards of a transition. Nondeterminism, however, is

rarely intended and only complicates planning. Addi-

tionally by restricting the number of tokens on a place

to one, the underlying net becomes safe and will be

easier to analyze. This restricts the expressiveness of

the net on the one hand, but makes planning and ana-

lyzing easier on the other hand. Although the change

of roles (i.e. binary relations) could also be modeled

by Transform nets as deﬁned above, we omitted them,

since we did not introduce ﬂexible assignments. The-

refore, in Figure 4.1 only attributes have been mode-

led.

5 EXAMPLE REVISITED

Let us return to the SD Net in Figure 4.1 again. We

will now explain the ﬁrst steps the net might take. We

have the following ontology and the following initial

DYNAMIC SERVICE COMPOSITION: A PETRI-NET BASED APPROACH

163

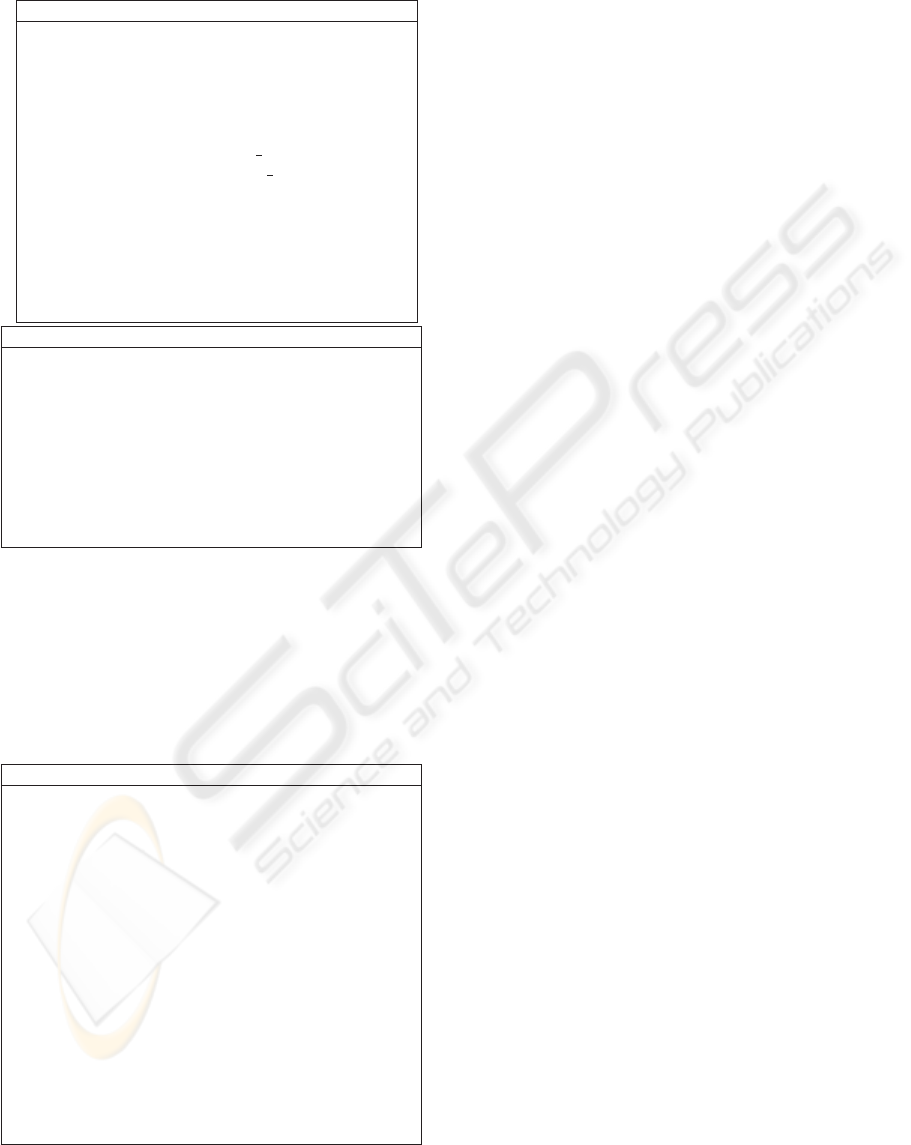
facts in our knowledge base:

Ontology (TBox)

FuelOrder

= Order 

quantity.ItemQuantity 

type.FuelType

AccountInformation

= currency.Currency 

balance.Decimal 

owner.Person 

acc number.integer 

bank code.integer

NotDeliverableFailure

= Failure  order.Order

Price

= amount.Decimal 

currency.Currency

DeliveryReceipt

= deliveryDate.Date 

order.Order 

price.Price

...

Facts (Abox) (initial)

FuelOrder(order1)

order1.quantity = quant1

order1.type = Diesel

ItemQuantity(quant1)

quant1.quantity = 200

quant1.unit = Gallon

AccountInformation(acc1)

acc1.currency = Euro

acc1.balance = 40000

...

After the message with the order arrives at the ser-

vice, the service looks up, whether the order quantity

can be delivered. If it cannot be delivered, the calling

agent receives a NotDeliverableFailure. If it can be

delivered, the agent receives a DeliveryReceipt and

the account corresponding to the AccountInformation

the agent has sent will have a reduced balance. After

the execution of the net, the knowlegde base might

contain the following statements:

Facts (Abox) (ﬁnal)

FuelOrder(order1)

order1.quantity = quant1

order1.type = Diesel

ItemQuantity(quant1)

quant1.quantity = 200

quant1.unit = Gallon

AccountInformation(acc1)

acc1.currency = Euro

acc1.balance = 39200

DeliveryReceipt(dr1)

dr1.deliveryDate = date1

dr1.order = order1

dr1.price = price1

date1.day=05

date1.month=12

price1.amount=800

price1.currency=Euro

...

The agent can now calculate the difference and rea-

son about what happens when it executes the service.

In this simple scenario we only have one service. It

is of course possible to have a much more complex

scenario with many different services. Another ma-

jor advantage of Petri nets as underlying formalism is

their support for reﬁnement. This allows us to build

classes of net fragments that correspond to classes of

services. Saying that a BuyService always involves

some kind of payment and some kind of delivery, we

can now reﬁne this basic structure in different ways

resulting in an ontology of services – an approach

very similiar to the one in (OWL Services Coalition,

2005).

The approach described in this paper has been pro-

totypically implemented using (R

ENEW, 2005, ) and

ROT

E, 2005, ). The SAND (Service Agent Net

Description) Plug-in is a plug-in of the R

ENEW Pe-

tri net simulation engine which allows to model and

execute Service Description Nets. It makes use of the

ROT

E API to import ontologies which can then

be used within an SD net. These ontologies can be

either P

ROT

E ﬁles or OWL ontologies. Since the

latter is a standardized exchange format, this format

is strongly encouraged. The current attribute values

of the net can be inspected by clicking on the corre-

sponding tokens in the simulation. This allows a user

to visually follow the steps and their impact on the

data. S

AND can automatically evaluate different nets

and can return the one best suited for a given task to

the user. Through this, an agent can select or preselect

workﬂows with the desired qualities. As for now this

planning is simply carried out by a depth-ﬁrst search,

which, however, may not terminate if the underlying

workﬂow net has an inﬁnite reachability graph.

6 CONCLUSION AND OUTLOOK

In this paper we have presented a formal framework

to model processes with data based on description lo-

gics, algebra and Petri nets. We see this as a step to-

ward a semantic description of processes as it is nee-

ded in the Semantic Web services and agent context.

Predicate/Transition nets (Genrich, 1986) have as

well used petri nets to model the modiﬁcation of lo-

gical terms. Service Description Nets, however, focus

more on the manipulation of information represented

by the terms deﬁned in an ontology.

Since Service Description Nets are closely related

to algebraic nets, analyzing techniques for algebraic

nets as e.g. discussed in (Reisig, 1991) can be app-

lied to Service Description Nets as well. Additionally,

this relationship guarantees the executability of these

nets. Further investigation has to show if the special

structure of Service Description Nets results in other

interesting properties and analysis techniques. Fur-

ICEIS 2006 - SOFTWARE AGENTS AND INTERNET COMPUTING

164

thermore it should be discussed to what extend it is

sensible to forget about the algebraic structure and re-

duce Service Description Nets to S/T-Nets or work-

ﬂow nets to study their behavioral properties.

As further research we will classify services ac-

cording to their behavior and their interface. This

will give us a semantic classiﬁcation of Web services

which will make planning much faster by selecting

only services from particular classes. Another topic

is the improvement of the planning and the conver-

sion of the representation to some XML dialect such

that we can import the process description of other

formats (e.g. OWL-S).

REFERENCES

Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and

Patel-Schneider, P. F., editors (2002). Description

Logic Handbook: Theory, Implementation and Ap-

plications. Cambridge University Press, Cambridge

(Mass.).

orger, E. and St

ark, R. (2003). Abstract State Machines –

A Method for High-Level System Design and Analysis.

Springer, Berlin et.al.

Ehrig, H. and Mahr, B. (1985). Equations and initial seman-

tics; Fundamentals of algebraic speciﬁcation. EATCS

Monographs on Theoretical Computer Science. Ber-

lin.

Genrich, H. J. (1986). Predicate/transition nets. In Brauer,

W., Reisig, W., and Rozenberg, G., editors, Advances

in Petri Nets, volume 254 of Lecture Notes in Compu-

ter Science, pages 207–247.

Giunchiglia, F. and Traverso, P. (1999). Planning as model

checking. In Biundo, S. and Fox, M., editors, ECP,

volume 1809 of Lecture Notes in Computer Science,

pages 1–20.

Goguen, J. A. and Meseguer, J. (1992). Order-sorted al-

gebra I: equational deduction for multiple inheritance,

overloading, exceptions and partial operations. Theor.

Comput. Sci., 105(2):217–273.

Kindler, E., Martens, A., and Reisig, W. (2000). Inter-

operability of workﬂow applications: Local criteria

for global soundness. In van der Aalst, W. M. P., De-

sel, J., and Oberweis, A., editors, Business Process

Management, volume 1806 of Lecture Notes in Com-

puter Science, pages 235–253.

ohler, M. and Ortmann, J. (2005). Formal aspects for

semantic service modeling based on high-level petri

nets. In Proceedings of the International Conference

on Intelligent Agents, Web Technologies and Internet

Commerce (IAWTIC) 2005.

OWL Services Coalition (2005). OWL-S1.1 Release. Tech-

nical report, ˙www.daml.org/services/owl-s/1.1/.

ROT

E (2005). The prot

e ontology editor and know-

ledge acquisition system. http://protege.stanford.edu/.

Provides references to programs, source code and do-

cumentation of the Prot

e tool set.

Reisig, W. (1991). Petri nets and algebraic speciﬁcations.

In Jensen, K. and Rozenberg, G., editors, High-level

Petri Nets – Theory and Application, pages 137–170,

Berlin, Heidelberg. Springer.

Reisig, W., Schmidt, K., and Stahl, C. (2005). Kommunizie-

rende workﬂow-services modellieren und analysieren.

Informatik - Forschung und Entwicklung.

ENEW (2005). RENEW – the reference net workshop.

http://www.renew.de/. Provides references to pro-

grams, source code and documentation of the Renew

tool set.

Staab, S. and Studer, R., editors (2004). Handbook on Onto-

logies. International Handbooks on Information Sys-

tems.

van der Aalst, W. M. P. (2003). Inheritance of interorga-

nizational workﬂows: How to agree to disagree wi-

thout loosing control? Inf. Tech. and Management,

4(4):345–389.

DYNAMIC SERVICE COMPOSITION: A PETRI-NET BASED APPROACH

165