
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES
IN LARGE PATTERN BASES: A BITMAP APPROACH
François Jacquenet, Christine Largeron and Cédric Udréa
EURISE - University of Saint-Etienne
23 rue Paul Michelon, F42023 Saint-Etienne, France
Keywords:
Pattern Management, Association Rules, Non-redundant Rules, Bitmap Arrays.
Abstract:
Knowledge Discovery from Databases has more and more impact nowadays and various tools are now avail-
able to extract efficiently (in time and memory space) some knowledge from huge databases. Nevertheless,
those systems generally produce some large pattern bases and then the management of these one rapidly be-
comes untractable.
Few works have focused on pattern base management systems and researches on that domain are really new.
This paper comes within that context, dealing with a particular class of patterns that is association rules. More
precisely, we present the way we have efficiently implemented the search for non redundant rules thanks to
a representation of rules in the form of bitmap arrays. Some experiments show that the use of this technique
increases dramatically the gain in time and space, allowing us to manage large pattern bases.
1 INTRODUCTION
Data mining, and more generally knowledge discov-
ery from databases, have really been an active re-
search area for the last decade. Volumes of data that
have to be processed are larger and larger and data
mining techniques are now varied and sophisticated.
Various researches aimed at designing more and more
efficient algorithms – in term of processing time and
memory space – to mine huge volumes of data and
commercial tools are now available for end user data
miner. Nevertheless, one of the main drawbacks of
these tools concerns the post processing step. Indeed,
when a data miner uses a data mining tool on some
data, he generally has no problem to parameterize it to
his specific needs, but he often has some difficulty to
interpret the results returned by this tool. In fact, what
generally makes this interpretation difficult is that he
is often overwhelmed by the quantity of patterns dis-
covered by his data mining tool.
We may distinguish two principal ways for solv-
ing this problem. The first one consists in trying,
during the data mining step, to avoid the generation
of a too large quantity of patterns, keeping only the
patterns that have an immediate interest for the user.
This approach has been followed in several ways. For
example, some algorithms only work on condensed
representations of the patterns during the mining step
(Boulicaut, 2005), (Zaki and Hsiao, 2005), (Wang
et al., 2005), (Wang and Han, 2004), (Pasquier et al.,
2005). Some algorithms push constraints in the fre-
quent pattern generation step in order to immediately
prune non relevant patterns during this phase (Ba-
yardo et al., 2000), (Zaki, 2001), (Garofalakis et al.,
2002), (Albert-Lorincz and Boulicaut, 2003), (Bouli-
caut and Jeudy, 2005). Nevertheless, even with such
techniques the users generally remain overwhelmed
with a large volume of patterns. Other algorithms try
to integrate various sophisticated interestingness mea-
sure (Freitas, 1999) to only discover the patterns that
seems to be interesting for the user, but this concept
of interestingness of patterns is difficult to define a
priori. Moreover, a user may want to process sev-
eral data mining steps, choosing various parameteri-
zations of his tool depending on the experiments he
is doing, and then want to manage the various sets of
patterns extracted.
Thus a second way, post-processing oriented, has
focused on pattern base management. The principle
consists in storing the patterns extracted by some data
mining systems using some efficient data structures.
Pattern manipulation languages have then to be de-
signed in order to manage them. Data mining lan-
guages integrated in database management systems
208
Jacquenet F., Largeron C. and Udréa C. (2006).
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES IN LARGE PATTERN BASES: A BITMAP APPROACH.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 208-215
DOI: 10.5220/0002495902080215
Copyright
c
SciTePress

(Boulicaut and Masson, 2005) offer some facilities for
pattern manipulation through post-processing opera-
tors. Nevertheless those one are very basic and pat-
tern base management systems should provide more
sophisticated functionalities. The PANDA project
(Catania et al., 2004) is an interesting way in that do-
main. It proposes a generic framework to model vari-
ous classes of patterns, then some SQL requests allow
the user to manage those pattern bases. Nevertheless,
as the underlying model used for storing the patterns
is the relational model, the requests one can write
are very complex, non intuitive and time consuming.
Also in the field of pattern base management, we may
cite the PMML project (Grossman et al., 1999) that
allow interoperability of pattern bases, specifying an
XML framework associated to the concept of pattern
and providing some facilities for managing them in
that form. (Zaki et al., 2005) also proposed a generic
framework for defining data structures and manage-
ment functionalities on patterns.
Our work is also part of this strategy that aims at
designing data structures and efficient algorithms for
large pattern base management. Indeed, we think that
it may be interesting for the users, to be able to get all
the patterns that may be extracted successively run-
ning data mining algorithms on various databases and
then to have efficient tools for post processing them.
More precisely, in this paper, we focus on the man-
agement of a particular class of patterns: the associa-
tion rules (Agrawal et al., 1993). In this domain, few
works have been done nowadays. The most signif-
icant one is probably RULE-QL (Tuzhilin and Liu,
2002) which proposes an extension of SQL allow-
ing some kind of management for association rules.
Nevertheless, such a language only offers some very
basic functionalities such as accessing some parts of
rules, searching for rules containing a particular item
in their left or right part, etc. In fact, on such patterns,
various management functions may be proposed and
we focus more particularly on the discovery of non
redundant rules in a set of association rules. This
task has already been studied in several researches
such as, for example, (Zaki, 2000), (Zaki, 2004),
(Bastide et al., 2000), (Li et al., 2004), (Li and Hamil-
ton, 2004), (Goethals et al., 2005). Nevertheless, all
these works aim at defining data mining algorithms
for extracting, from large databases, the non redun-
dant rules, and only these one. Our work is differ-
ent in that sense that it is based on a post process-
ing approach, dealing with patterns and not directly
data. Thus, we want, from a set of patterns (associa-
tion rules), being able to extract all the non redundant
one.
The next section recalls some basic definitions
useful for understanding the paper. The section 3
presents some data structures that can be used for
storing association rules. We first present a basic ap-
proach and then another one based on bitmap arrays.
The section 4 shows how one can take advantage of
this former structure to evaluate the non redundancy
of one rule with respect to another one. The section 5
presents an algorithm for extracting all the non redun-
dant rules from a large rule base. A set of experiments
shows the efficiency of our approach based on bitmap
arrays with respect to the more basic one.
2 DEFINITIONS
Let us consider a database δ ⊆ I × T where I =
{1, 2, .., k} is an itemset, T = {1, 2, ..., l} is a set of
transactions and such that if an item i from I is in a
transaction t from T , then (i,t) ∈ δ. A set X ⊆ I is
called an itemset and its support, noted |X|, is equal
to the number of transactions containing X.
2.1 Association Rules
An association rule is an expression of the form
B → H where B = {B
1
, ..., B
n
} and
H = {H
1
, ..., H
m
} are some itemsets such that
{B
1
, ..., B
n
}
{H
1
, ..., H
m
} = ∅. Each rule may be
characterized by its support and confidence.
Support of an association rule
The support of an association rule of the form B →
H is equal to the number of transactions that contain
the itemsets B and H divided by the total number of
transactions in the database:
Support(B → H)=
|BH|
l
where l is the number of transactions in the database
and |BH| is the number of transactions in the data-
base that contain the itemsets B and H.
Confidence of an association rule
The confidence of an association rule of the form
B → H is equal to the number of transactions of the
database that contain the itemsets B and H divided
by the number of transactions that contain the itemset
B:
Confidence(B → H)=
|BH|
|B|
2.2 Non Redundant Association
Rules
Many definitions have been proposed in the literature
concerning the concept of non redundant rules. For
example, (Bastide et al., 2000) propose the following
definition.
Definition: An association rule of the form B → H
is non redundant if there exists no rule of the form
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES IN LARGE PATTERN BASES: A BITMAP
APPROACH
209

B
→ H
with the same support and confidence such
that B
⊆ B et H ⊆ H
.
Many other definitions have been proposed, we
may cite for example (Aggarwal and Yu, 1998), (Zaki,
2000), (Goethals et al., 2005), or the close definition
of basic rule in (Li and Hamilton, 2004). In order to
make the paper clearer, we will use, in the remaining
of the paper, the following definition:
Definition: A rule of the form B → H is non re-
dundant if and only if there exists no rule of the form
B
→ H
such that B
⊆ B and H ⊆ H
.
Nevertheless, our work could easily be extended to
be based on the full definition of (Bastide et al., 2000)
taking into account the support and confidence, but
also the various other definitions.
3 STORING ASSOCIATION
RULES
Before presenting an efficient algorithm for discover-
ing non redundant rules in a large rulebase, it is es-
sential to define an efficient data structure for storing
those rules.
3.1 Basic Storage of Association
Rules
The most basic storage technique that can be used to
store some association rule consists in using a single
table, we call RULES, having three attributes:
• idrule: the identifier of the rule.
• idpart: the identifier of the part (1 for the left part
of the rule, 2 for the right one).
• iditem: the identifier of the item.
Example: Let us consider I={A,B,C,D,E,F}, and the
rules R = {A, C}→{D, E} and R
= {A}→
{B,D,E}. The table RULES contains the following
information:
idrule idpart iditem
1 1 A
1 1 C
1 2 D
1 2 E
2 1 A
2 2 B
2 2 D
2 2 E
With this storage technique, the table contains as
much rows as the number of rules multiplied by the
number of items per rule. It is generally too large to
be stored in main memory by the DBMS, which slows
down the processing time due to the large number of
hard disk accesses. This is the reason why we used
another storage technique based on bitmap arrays.
3.2 Storing Rules with Bitmap
Arrays
(Morzy and Zakrzewicz, 1998) proposed the concept
of bitmap arrays for storing association rules. With
this approach, each part of an association rule con-
tains as many bits as the total number of items in the
database of transactions. Each bit of the bitmap array
is then associated to a particular item and the value of
this bit is equal to ’1’ if and only if the correspond-
ing item appears in the part of the rule associated to
the bitmap array. The binary coding of bitmap arrays
reduces the storage cost and avoids access to data in
order to count the number of items in a rule or in the
result of a logical operation. Thus, as we will see later
in the experimental section, using bitmap arrays dra-
matically reduces the processing time while searching
for non redundant rules in a large rulebase.
Many works have used this representation of the
rules in the framework of mining frequent patterns in
order to optimize the algorithm designed. For exam-
ple we may cite (Masson et al., 2004), (Pucheral et al.,
1998), (Louie and Lin, 2000), etc.
In such a context, an association rule may then
be stored in a table that contains two attributes:
LeftP art and RightP art. Those attributes are
bitmap arrays whose size is equal to the number of
items of I, the set of all the items in the database of
transactions.
Example: Let us consider I={A,B,C,D,E,F}. The
rule R = {A, C}→{D, E} is stored using the two
following arrays:
Array LeftPart of R:
Item F E D C B A
Bit value 0 0 0 1 0 1
Array RightPart of R:
Item F E D C B A
Bit value 0 1 1 0 0 0
In the same way, the rule R
= {A}→{B,D,E} is
represented by the two following arrays:
Array LeftPart of R’
Item F E D C B A
Bit value 0 0 0 0 0 1
Array RightPart of R’
Item F E D C B A
Bit value 0 1 1 0 1 0
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
210

At the same time, all the name of the tables asso-
ciated to each rule are stored in a global table COL-
LECTION which contains as much rows as the num-
ber of rules. This approach has several advantages.
First, each rule is stored independently from the oth-
ers. Secondly, the table COLLECTION is the only
one that can become too large and make the system
down. Nevertheless, the size of this table only de-
pends on the number of rules and not of the number of
items per rule contrary to the table RULES in the clas-
sical storage technique. Finally, if we have to manage
several sets of association rules, it is possible to create
several tables COLLECTION, which avoids to dupli-
cate the rules contained in several distinct sets.
3.3 Using the Logical Operator AND
As we have previously noticed, one of the advantages
of bitmap arrays is that we may use some logical oper-
ators on them while managing rules. For example, we
may use the logical operator AND. The result of ap-
plying an AND between two bitmap arrays is a bitmap
array that contains a value ’1’ for the item at the index
i if the two bitmap arrays contain a ’1’ for the item at
the index i.
Thus, using the rules of the previous example,
RightPart of R AND RightPart of R’ returns the fol-
lowing array:
RightPart of R 0 1 1 0 0 0
RightPart of R’ 0 1 1 0 1 0
AND 0 1 1 0 0 0
To determine the number of items associated with a
bitmap array, we only have to count the number of ’1’
in it.
4 EVALUATING THE NON
REDUNDANCY OF ONE RULE
4.1 With the Basic Storage
If the set of association rules is stored using the
classical representation, that is using the single ta-
ble RULES presented in the previous section, search-
ing for non redundant rules in it leads to traverse the
whole table. To determine if a rule R is non redundant
with respect to a rule R
, we have to compare the left
parts of R and R
and then their right parts. To do so,
we have to join the table RULES with itself.
The SQL request used to determine if the left part
of a rule R is not included in the left part of a rule R
is this one:
SELECT iditem
FROM RULES
WHERE
idrule=R
AND part=1
AND iditem NOT IN
(SELECT iditem
FROM RULES
WHERE
idrule=R’
AND part=1);
Processing right parts leads to a similar SQL request.
We may observe that the processing time depends
on the number of items per rule and on the number
of rules in RULES. Furthermore, join operator being
time consuming, this first solution does not seem to
be the best one and it seems preferable not to do such
operations on the RULES which is usually huge.
4.2 With Bitmap Arrays
We show the way we determine the non redundancy
of a rule with respect to another rule using the effi-
cient representation of rules based on bitmap arrays.
This will allow us, in the next section, to present an
algorithm for discovering all the non redundant rules
from a rulebase. This algorithm will not reduce the
number of tests to be done, but it will allow us to
never process any join and consequently to dramati-
cally decrease the processing times. This algorithm
makes the most of a property of bitmap arrays with
respect to redundancy of rules.
Let R = B → H and R
= B
→ H
be two as-
sociation rules defined by B = {B
1
, ..., B
n
},H =
{H
1
, ..., H
m
},B
= {B
1
, ..., B
n
} and H
=
{H
1
, ..., H
m
} on I = {1, ..., k}.
Let us recall that, in this paper, we consider that
an association rule R = B → H is non redundant if
there exists no rule R
= B
→ H
such that B
⊆ B
and H ⊆ H
.
We call IB
X
= {IB
X
1
, ..., IB
X
k
} the bitmap ar-
ray corresponding to the left part of the rule X and
IH
X
= {H
X
1
, ..., IH
X
k
} the bitmap array corre-
sponding to the right part of the rule X where IB
X
i
is equal to 1 if the item i is contained in the left part
of X, 0 else, and IH
X
i
is equal to 1 if the item i is
contained in the right part of X, 0 else.
We note (R AND R
) the rule having as a left (resp.
right) part the intersection of the left (resp. right) parts
of the rules R and R
:
(RANDR
)=B ∩ B
→ H ∩ H
Proposition: The rule R is redundant with respect to
the rule R
if and only if IB
(RANDR
)
=IB
R
and
IH
(RANDR
)
=IH
R
.
Proof:
Let us show that if R is redundant with respect to R
then IB
(RANDR
)
=IB
R
and IH
(RANDR
)
=IH
R
.
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES IN LARGE PATTERN BASES: A BITMAP
APPROACH
211
Due to the way bitmap arrays are constructed,
IB
(RANDR
)
is the intersection of the left parts of
the rules R and R
.
So, if R is redundant with respect to R
then IB
R
⊆
IB
R
.
Thus, IB
(RANDR
)
=IB
R
∩ IB
R
=IB
R
.
In the same way, IH
(RANDR
)
is the intersection of
the right parts of the rules R and R
.
So, if R is redundant with respect to R
then IH
R
⊆
IH
R
.
Thus, IH
(RANDR
)
=IH
R
∩ IH
R
=IH
R
.
In conclusion, if R is redundant with respect to R
then IB
(RANDR
)
=IB
R
and IH
(RANDR
)
=IH
R
.
Reciprocal:
Let us demonstrate that if R is not redundant with
respect to R
then IB
(RANDR
)
= IB
R
or
IH
(RANDR
)
= IH
R
.
By definition, if R is non redundant with respect to
R
then B
is not included in B or H is not included
in H
.
If B
is not included in B, then IB
R
∩IB
R
= IB
R
.
So IB
(RANDR
)
=IB
R
∩ IB
R
. Thus,
IB
(RANDR
)
= IB
R
.
Else, H is not included in H
, then
IH
R
∩ IH
R
= IH
R
.
So IH
RANDH
=IH
R
∩ IH
R
and consequently
IB
(RANDR
)
= IB
R
. qed.
Example: If we consider again the two rules given
as example in the previous section we may see that R
is redundant with respect to R
. Indeed, the bitmap
array LeftPart of (R AND R
) is equal to (000001):
LeftPart of R 0 0 0 1 0 1
LeftPart of R’ 0 0 0 0 0 1
AND 0 0 0 0 0 1
The bitmap array LeftPart of (R AND R
) is equal to
the bitmap array RightPart of R
.
In the same way, the bitmap array RightPart of (R
AND R
) is equal to (011000), indeed:
RightPart of R 0 1 1 0 0 0
RightPart of R’ 0 1 1 0 1 0
AND 0 1 1 0 0 0
So, the bitmap array RightPart of (R AND R
)is
equal to the bitmap array RightPart of R.
If the right part of R
had been {B,E,F}, then
R would not had been redundant with respect to R
.
Indeed, the bitmap array RightPart of (R AND R
)
would have been equal to (010000):
RightPart of R 0 1 1 0 0 0
RightPart of R’ 1 1 0 0 1 0
AND 0 1 0 0 0 0
So the bitmap array RightPart of (R AND R
)isnot
equal to the bitmap array RightPart of R.
5 SEARCHING FOR NON
REDUNDANT RULES IN A
RULE BASE
We now present the algorithm 1 designed for search-
ing for non redundant rules in a rulebase and using
the property demonstrated in the last section. From
a list RuleList containing the set of N rules to be
tested, it returns an array NRR of size SizeNRR in
which each non redundant rule found by the algorithm
is stored.
Algorithm 1 ExtractNonRedundantRules
Input: RuleList, an set of association rules
Output: NRR, the set of all the non redundant
rules extracted from RuleList
begin
NRR[1] ← RuleList[1]; SizeNRR ← 1;
for i ← 2 to N do
j=1;
while j<=SizeNRR And RuleList[i] is
non redundant with respect to NRR[j] do
if NRR[j] is non redundant with re-
spect to RuleList[i] then
j ← j+1;
else
NRR[j] ← NRR[SizeNRR];
Delete NRR[SizeNRR];
SizeNRR ← SizeNRR-1;
while j<=SizeNRR do
if NRR[j] is non redundant
with respect to RuleList[i]
then
j ← j+1;
else
NRR[j] ←
NRR[SizeNRR];
Delete NRR[SizeNRR];
SizeNRR ← SizeNRR-
1;
end
end
end
end
if j=SizeNRR+1 then
NRR[SizeNRR+1] ← RuleList[i];
SizeNRR ← SizeNRR+1;
end
end
end
The array NRR is built in such a way that the rules
it contains are non redundant the ones against the oth-
ers. This principle allows us to decrease the number
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
212
of redundancy tests. Indeed, if a rule j of NRR is
redundant with respect to a rule i of RuleList,itis
useless to test if the rule i is redundant with respect
to the other rules of NRR because it is impossible.
Indeed, let us suppose it exists a rule k of NRR such
that the rule i was redundant with respect to the rule
k. Then, as the rule j is redundant with respect to the
rule i, in that case, B
i
⊆ B
j
and H
j
⊆ H
i
. Similarly,
the rule i being redundant with respect to the rule k
we have B
k
⊆ B
i
and H
i
⊆ H
k
. Thus, B
k
⊆ B
j
and
H
j
⊆ H
k
by transitivity, which means that the rule
j of NRR is redundant with respect to the rule k of
NRR which contradicts the way we construct NRR.
6 EXPERIMENTS
We have made several experiments to compare the
processing time needed to extract non redundant rules
from a set of rules using the basic approach and the
bitmap one. In the two cases the global number of
rules of the base and the number of non redundant
rules it contains may have an influence on the effi-
ciency, thus some experiments have been done vary-
ing successively those two parameters. We also have
studied the influence of the number of items per rule
on the efficiency of the system.
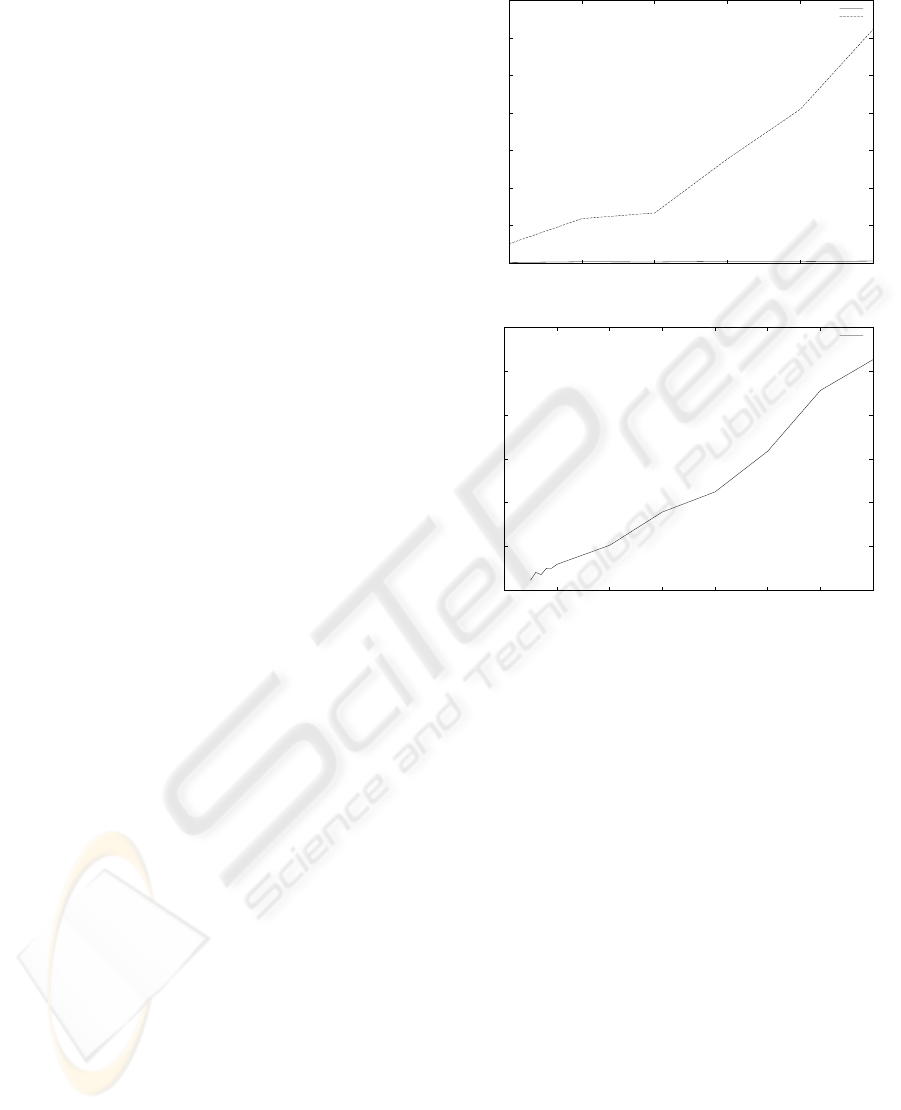
The first experiment (figures 1(a) and 1(b)) studies
the influence of the total number of rules in the pat-
tern base on the processing time needed to discover all
the non redundant rules. The bitmap array approach
is really more efficient than the classical one which
is between 20 to 100 times slower. Moreover, even
if the processing time increases with the number of
rules in the two approaches, the increase is stronger
for the classical one. The processing time with the
bitmap array approach remains reasonable even for
7000 rules (approximately 4 minutes) while it takes
approximately one hour with the classical approach
for processing 1000 rules.
The second experiment (figures 2(a) and 2(b)) stud-
ies the time needed to discover the non redundant
rules, depending on their number. The results are
rather encouraging: the bitmap approach is between
37 and 50 times faster than the basic approach and
the increase of the processing time with the number of
non redundant rules is lower for the bitmap approach
than for the basic one.
The last experiment, which studies the influence of
the number of items per rule on the processing time
3(a) et 3(b)), confirms the previous results: the ba-
sic approach is strongly influenced by the number of
items per rule (more than 9 times slower between 8
and 30 items per rule) while the bitmap one is less in-
fluenced by that (less than two times slower between
8 and 30 items per rule). In terms of processing time,
0
500
1000
1500
2000
2500
3000
3500
500 600 700 800 900 1000
Time in seconds
Number of rules
Bitmap array approach
Basic approach
(a)
0
50
100
150
200
250
300
0
1000 2000 3000 4000 5000 6000 7000
Time in seconds
Number of rules
Bitmap array approach
(b)
Figure 1: Processing time depending on the number of
rules.
the bitmap approach is really acceptable (with a max-
imum of 26 seconds) while the basic one exceeds one
hour for processing a rule base where rules contain 30
items.
Finally we have studied the influence of the global
number of items used in the whole rulebase. This ex-
periment have shown that the efficiency of the two
approaches was similar and that this parameter does
not have any influence on it.
7 CONCLUSION AND FUTURE
WORKS
In view of the large pattern bases that can be gener-
ated nowadays by various efficient data mining algo-
rithms, it becomes essential to have efficient tools for
pattern management. In this paper, we were interested
in association rules and more precisely the rapid dis-
covery of non redundant rules from large rulebases.
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES IN LARGE PATTERN BASES: A BITMAP
APPROACH
213

0
200
400
600
800
1000
1200
1400
1600
1800
10 15 20 25 30 35 40 45 50
Time in seconds
Number of non redundant rules
Bitmap array approach
Basic approach
(a)
16
18
20
22
24
26
28
30
32
10 15 20 25 30 35 40 45 50
Time in seconds
Number of non redundant rules
Bitmap array approach
(b)
Figure 2: Processing time depending on the number of non
redundant rules to be discovered.
To do so, we have considered the use of bitmap ar-
rays and the logical operator AND. The experiments
we made have shown that this approach is dramati-
cally more efficient than the basic one, allowing us to
process large pattern bases in linear time.
Our research aims at designing a more general
framework for a pattern base management system and
thus we have to develop the work presented here in
several ways. For example, using bitmap arrays for
coding association rules may allow us to design other
rule management operators such as discovering rules
that contain a given set of items, or rules that contra-
dict a given hypothesis, etc.
At the same time, we want to investigate the storage
and management of other classes of patterns such as
clusters, decision trees, etc.
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
5 10 15 20 25 30
Time in seconds
Number of items per rules
Bitmap array approach
Basic approach
(a)
16
17
18
19
20
21
22
23
24
25
26
27
5 10 15 20 25 30
Time in seconds
Number of items per rule
Bitmap array approach
(b)
Figure 3: Processing time depending on the number of
items per rule.
REFERENCES
Aggarwal, C. C. and Yu, P. S. (1998). Online generation of
association rules. In Proceedings of the 14th Confer-
ence on Data Engineering, pages 402–411, Orlando.
Agrawal, R., Imielinski, T., and Swami, A. (1993). Mining
association rules between sets of items in large data-
bases. In Proceedings of the ACM SIGMOD Inter-
national Conference on Management of Data, pages
207–216, Washington D.C.
Albert-Lorincz, H. and Boulicaut, J.-F. (2003). Mining fre-
quent sequential patterns under regular expressions:
A highly adaptive strategy for pushing contraints. In
Proceedings of the Third SIAM International Confer-
ence on Data Mining, San Francisco, CA, USA, May
1-3, 2003.
Bastide, Y., Pasquier, N., Taouil, R., Stumme, G., and
Lakhal, L. (2000). Mining minimal non-redundant
association rules using frequent closed itemsets. In
Proceedings of the first International Conference on
Computational Logic, LNCS 1861, pages 972–986.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
214

Bayardo, R., Agrawal, R., and Gunopulos, D. (2000).
Constraint-based rule mining in large, dense data-
bases. Data Mining and Knowledge Discovery,
4(2/3):217–240.
Boulicaut, J. and Jeudy, B. (2005). Constraint-based data
mining. In The Data Mining and Knowledge Discov-
ery Handbook, pages 399–416. Springer.
Boulicaut, J. F. (2005). Condensed representations for data
mining. In Encyclopedia of Data Warehousing and
Mining, pages 207–211. Idea Group Reference.
Boulicaut, J. F. and Masson, C. (2005). Data mining query
languages. In The Data Mining and Knowledge Dis-
covery Handbook, pages 715–727. Springer.
Catania, B., Maddalena, A., Mazza, M., Bertino, E., and
Rizzi, S. (2004). A framework for data mining pat-
tern management. In Proceedings of the 8th European
Conference on Principles and Practice of Knowledge
Discovery in Databases, LNCS 3202, pages 87–98.
Freitas, A. A. (1999). On rule interestingness measures.
Knowledge-Based Systems, 12(5-6):309–315.
Garofalakis, M. N., Rastogi, R., and Shim, K. (2002). Min-
ing sequential patterns with regular expression con-
straints. IEEE Transactions on Knowledge and Data
Engineering, 14(3):530–552.
Goethals, B., Muhonen, J., and Toivonen, H. (2005). Min-
ing non-derivable association rules. In Proceedings of
the fifth SIAM International Conference on Data Min-
ing, Newport Beach, California, USA, April 21-23.
Grossman, R. L., Bailey, S., Ramu, A., Malhi, B., Hall-
strom, P., Pulleyn, I., and Qin, X. (1999). The man-
agement and mining of multiple predictive models us-
ing the predictive model markup language (PMML).
In Information and Software Technology, volume 41,
pages 589–595.
Li, G. and Hamilton, H. (2004). Basic association rules.
In Proceedings of the fourth SIAM International Con-
ference on Data Mining, Lake Buena Vista, Florida,
USA, April 22-24. SIAM.
Li, Y., Liu, Z. T., Chen, L., Cheng, W., and Xie, C. H.
(2004). Extracting minimal non-redundant associa-
tion rules from QCIL. In International Conference on
Computer and Information Technology, pages 986–
991. IEEE Computer Society.
Louie, E. and Lin, T. Y. (2000). Finding association rules
using fast bit computation: Machine-oriented model-
ing. In Proceedings of the 12th International Sympo-
sium on Methodologies for Intelligent Systems, LNCS
1932, pages 486–494. Springer.
Masson, C., Robardet, C., and Boulicaut, J. F. (2004). Opti-
mizing subset queries: a step towards sql-based induc-
tive databases for itemsets. In Proceedings of the 2004
ACM symposium on Applied computing (SAC’04),
pages 535–539. ACM Press.
Morzy, T. and Zakrzewicz, M. (1998). Group bitmap in-
dex: A structure for association rules retrieval. In Pro-
ceedings of the Fourth International Conference on
Knowledge Discovery and Data Mining, pages 284–
288. AAAI Press.
Pasquier, N., Taouil, R., Bastide, Y., Stumme, G., and
Lakhal, L. (2005). Generating a condensed represen-
tation for association rules. Journal of Intelligent In-
formation Systems, 24(1):29–60.
Pucheral, P., Gardarin, G., and Wu, L. (1998). Bitmap based
algorithms for mining association rules. In Actes des
Journées Bases de Données Avancées (BDA’98).
Tuzhilin, A. and Liu, B. (2002). Querying multiple sets
of discovered rules. In Proceedings of the Eighth
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, pages 52–60. ACM.
Wang, J. and Han, J. (2004). BIDE: Efficient mining of
frequent closed sequences. In Proceedings of the 20th
International Conference on Data Engineering, ICDE
2004, 30 March - 2 April 2004, Boston, MA, USA,
pages 79–90.
Wang, J., Han, J., Lu, Y., and Tzvetkov, P. (2005). TFP: An
efficient algorithm for mining top-k frequent closed
itemsets. IEEE Transactions on Knowledge and Data
Engineering, 17(5):652–664.
Zaki, M. J. (2000). Generating non-redundant association
rules. In
Proceedings of the sixth ACM SIGKDD in-
ternational conference on Knowledge discovery and
data mining, August 20-23, 2000, Boston, MA, USA,
pages 34–43.
Zaki, M. J. (2001). SPADE: An efficient algorithm
for mining frequent sequences. Machine Learning,
42(1/2):31–60.
Zaki, M. J. (2004). Mining non-redundant association rules.
Data Mining and Knowledge Discovery, 9(3):223–
248.
Zaki, M. J. and Hsiao, C. (2005). Efficient algorithms
for mining closed itemsets and their lattice structure.
IEEE Transactions on Knowledge and Data Engineer-
ing, 17(4):462–478.
Zaki, M. J., Parimi, N., De, N., Gao, F., Phoophakdee, B.,
Urban, J., Chaoji, V., Hasan, M. A., and Salem, S.
(2005). Towards generic pattern mining. In Proceed-
ings of the Third International Conference on Formal
Concept Analysis, pages 1–20.
EFFICIENT MANAGEMENT OF NON REDUNDANT RULES IN LARGE PATTERN BASES: A BITMAP
APPROACH
215
