A DISCRETE PARTICLE SWARM ALGORITHM

FOR OLAP DATA CUBE SELECTION

Jorge Loureiro

Departamento de Informática, Instituto Superior Politécnico de Viseu,

Escola Superior de Tecnologia de Viseu, Campus Politécnico de Repeses, 3505-510 Viseu, PORTUGAL

Orlando Belo

Departamento de Informática, Escola de Engenharia,

Universidade do Minho, Campus de Gualtar, 4710-057 Braga, PORTUGAL

Keywords: Data Cube Selection, Data Warehousing, Discrete Particle Swarm Algorithm, OLAP, Multidimensional

databases.

Abstract: Multidimensional analysis supported by Online Analytical Processing (OLAP) systems demands for many

aggregation functions over enormous data volumes. In order to achieve query answering times compatible

with the OLAP systems’ users, and allowing all the business analytical views required, OLAP data is

organized as a multidimensional model, known as data cube. The materialization of all the data cubes

required for decision makers would allow fast and consistent answering times to OLAP queries. However,

this also imply intolerable costs, concerning to storage space and time, even when a data warehouse had a

medium size and dimensionality - this will be critical on refreshing operations. On the other hand, given a

query profile, only a part of all subcubes are really interesting. Thus, cube selection must be made aiming to

minimize query (and maintenance) costs, keeping as a constraint the materializing space. That is a complex

problem: its solution is NP-hard. Many algorithms and several heuristics, especially of greedy nature and

evolutionary approaches, have been used to provide an approximate solution. To this problem, a new

algorithm is proposed in this paper: particle swarm optimization (PSO). According to our experimental

results, the solution achieved by the PSO algorithm showed a speed of execution, convergence capacity and

consistence that allow electing it to use in data warehouse systems of medium dimensionalities.

1 INTRODUCTION

Today’s business environments are very dynamic,

changing so fast that brings new opportunities for

everybody at all times. However, as we know, they

also bring new threats. It is crucial for the

enterprises to be able to answer to ones and others,

making timely, interrelated and adjusted decisions in

useful time. Moving in an uncertain environment,

decision makers expect for something that guide and

help them in their daily activities. This reality turned

information into the new Grail, in which search all

organizations are involved, leading them to the

building of data warehouses (DW). The availability

of reliable data for analysis made it possible for the

decision makers to acknowledge what the data really

says about their businesses. This imposed the

emergence of new systems, with new abilities,

capable of allowing decision makers to investigate

their data resources according to different business

perspectives, and surf through them according to the

result of previous observations. The systems that

enable this kind of analysis were coined in (Codd et

al., 1993) as OLAP systems. These systems, in

which data is organized in a multidimensional and

hierarchical way, known as data cube or multicube

(Chaudhuri & Dayal, 1997), allow sophisticated

OLAP operations such as drill-down, roll-up,

pivoting or slicing and dicing, all of them a

consequence of a typical profile of a session of

OLAP queries (mainly of aggregated nature). All

these interesting OLAP characteristics provide

access to data and querying satisfaction with

excellent processing time. If the aggregated data was

Loureiro J. and Belo O. (2006).

A DISCRETE PARTICLE SWARM ALGORITHM FOR OLAP DATA CUBE SELECTION.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 46-53

DOI: 10.5220/0002496000460053

 SciTePress

pre-computed and stored, the answer would be

almost immediate. Although, usually, that would

also imply a huge storing space and, specially, lots

of time to update the already aggregated data, once

its number is of

∏

, where h

is the number of

hierarchies of i dimension and d the number of

dimensions.

The aggregated data stored in a cube may be

conceptually represented as a Lattice (Harinarayan

et al., 1996), a direct acyclic graph where each

vertex has a subcube or cuboid (result of a Group-

By), and each edge represents a dependency relation,

that shows whose subcubes may be used to compute

others. Only a part of the possible subcubes can be

stored in the repository, being then mandatory to

select the most beneficial ones – concerning to

minimizing query and possibly maintenance costs –,

a problem that is characteristically NP-hard

(Harinarayan et al., 1996), known as data cube

selection problem. Some constraints may be applied

to the problems’ solution as materializing space or

maintenance time.

The rest of the paper is organized as follows. In

section 2, we reference and describe briefly some

works related with the problem that we address in

this paper. Section 3 introduces evolutionary

algorithms, detailing to discrete particle swarm

algorithm. Next, in section 4 we formalize the cube

selection problem, where a cost model is discussed

and where we show how to apply the proposed

algorithm to the problem. Section 5 describes the

experimental evaluation of the algorithm and the

obtained results. At last, section 6 concludes the

paper and presents some future work proposals.

2 RELATED WORK

We have already seen that data cubes and view

materialization are two possible conditions to

improve performance. Its materialization and

especially its maintenance imply special storage

space and execution time. As users change their

needs, the “optimal” materialized cube becomes far

from optimal, which makes mandatory its

recalibration – its extension and frequency are

directly related. Big restructurings may occur at

large intervals and some refining may take place in

short intervals or in almost real time. So, in terms of

characterization, we will have the so called static

and dynamic aggregation selections, or even its pro-

active selection or restructuring. In this paper we

restrict the discussion to the static approach, once it

is directly related with the scope of the present work.

Most of the proposals appear in the static selection

domain. In (Harinarayan et al. 1996) it was

approached for the first time the materializing views

selection problem to support OLAP multi-

dimensional analysis. It was proposed then a greedy

algorithm to solve the problem. Latter, an extension

to this proposal, was made in (Gupta et al., 1997),

which also included indexes selection.

Despite the greedy characteristics of the proposed

algorithms, its scalability is not easy. In (Baralis et

al., 1997) the query load profile is taken into account

for the views selection, while in (Shukla et al. 1998)

was proposed another change to the greedy

algorithm, also to improve the application scalability

of the algorithms: it selects the views accordingly to

its size. This proposal is much more efficient,

keeping the same quality of the others. (Shukla et

al., 2000) proposed a multicube algorithm where the

problem was focused from a different view: it is

supposed that all aggregations are computed not

from a single cube, but for multicube data models. A

systematic methodology for the materializing views

selection appeared in 1997 in (Gupta, 1997),

spreading the aggregated queries to a more general

form, those that can be represented by a AND-OR

graph. In (Gupta & Mumick, 1999), besides the

space for the materialized views, its maintenance

cost is also considered. This same problem is also

discussed in (Liang et al., 2001).

Other approaches, in a different domain, were

also attempted and proposed: the research for

solutions using evolutionary or random techniques.

Thus, there is some work devoted to the application

of genetic algorithms (Horng et al., 1999; Zhang et

al. 2001; Lin & Kuo, 2004) or random search in

(Kalnis et al., 2002).

3 EVOLUTIONARY AND

PARTICLE SWARM

ALGORITHMS

3.1 Biological Mimic Algorithms

Several search algorithms have a biological

motivation, trying to mimic a characteristic aspect of

what can be called “life”. There is a simple reason:

life (as its biological basic aspect or, at a higher

level, as the social and cognitive behaviour), is a

perpetual process of adaptation to environmental

conditions, requiring a continuous demand of

A DISCRETE PARTICLE SWARM ALGORITHM FOR OLAP DATA CUBE SELECTION

solutions in face of succeeding new problems. The

best known algorithms in this huge domain are: 1)

evolutionary algorithms, where the most

representatives and most used are probably genetic

algorithms; 2) swarm algorithms, that may take the

form of particle swarm algorithms and ant colony

optimization; and, finally, 3) artificial immune

systems. As we said previously, in section 2, only

the first ones have already been applied to cube

selection in a centralized DW. Swarm algorithms

have an application domain which may intercept the

former ones, and, then, it is natural to intend to apply

them to the same problem.

3.2 Discrete Particle Swarm

Algorithm

The authors of the PSO were trying to simulate a

bird flock (a simplified social system), modelling a

social and cognitive behaviour. After many

modifications, the authors realized that the

conceptual model was, in fact, an optimizer, that was

proposed in (Kennedy & Eberhart, 1995; Eberhart &

Kennedy, 1995). This approach assumes a

population of individuals, represented as binary

strings or real-valued vectors (particles), whose

position in an n-dimensional space will bring its

instant fitness. This position may be altered by the

application of an interactive procedure that uses a

velocity vector, allowing a progressively best

adaptation. It also assumes that individuals are social

by nature, and thus capable of interacting with

others, within a given neighbourhood. For each

individual, there are two main types of information

available: the first one is his own past experiences

(known as individual knowledge), the pbest (particle

best) position, and the other one is related to the

knowledge about its neighbour’s performance

(referred as cultural transmission), gbest (global

best) position.

There are two main versions of the PSO

algorithm: 1) the initial version, a continuous one,

where the particles move in a continuous space; and

2) the discrete or binary version, proposed in

(Kennedy & Eberhart, 1997), where the space is

discretized. Although similar, the spatial evolution

of particles in the former is addictive and

continuous, meaning that its next location is

computed adding the velocity to the position where

the particle is at the moment. The discrete space

does not allow the addictive continuous relation

space-velocity. It is substituted by the introduction

of the probabilistic space: the particle’s position will

be given by a probability dependent of its velocity,

using the rule

0;1)(()

111

==<

+++

elsethensigrndif

(1),

where

)exp(1

)(

sig

−+

, being

v the velocity

of the particle i at the k

iteration. The location of

the particle is now a state. The direct and

deterministic relation between space and velocity is

discarded. A casualistic vector is introduced – even

if the particle maintains the same velocity, its state

may change. The formula that rules the particle’s

dynamic concerning to velocity is:

().( ) ().( )

kk k k

ii i i

w rnd pbest rnd gbest

vv s s

=+ −+ −

(2),

meaning that changes in the particle’s velocity are

affected by its past velocity and by a vector that

tends to push it to its best past location, related to its

own past success knowledge – pbest, and another

vector, that pushes it to the best position already

reached by any particle, corresponding to the global

knowledge - gbest. To prevent the system from

running away, when particle oscillation becomes too

high, the velocity of the particle is limited by a Vmax

parameter and the following rule:

max max ma x max

,;,

iii i

if then if then

vv vv v v v v

>=< =−

−

(3).

This rule conceptually means that a limit is

imposed to the maximal probability of a bit to

achieve the 0 or the 1 value. Since the sigmoid

function is used, the exploration of new solutions is

encouraged if Vmax is short, in opposition to the

expected behaviour in continuous PSO.

4 THE COST MODEL AND THE

ALGORITHM

4.1 The Cost Model

The aim of an OLAP system is to minimize query

costs, maintaining maintenance costs at a minimal

level, satisfying a constraint, in this case,

materializing space. To do this, we use the linear

cost model proposed in (Harinarayan et al., 1996),

where the cost of a query answer is proportional to

the number of non-null cells of the used subcube. As

an OLAP query may be represented by the

corresponding subcube, the total query costs are:

(, )

qCq M

∑

, where

is the query frequency

of query q

and

(, )iCq M

is the cost of query

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

answering of query q

, supposing a materialized cube

M. Using the least ancestor notion, and linear cost

model,

(, ) min(| |,| (, )|)iiiC q M S Lanc q M=

As for the maintenance costs, we shall consider,

to simplify the discussion, a DW environment that

has only new tuples in the fact tables. We shall also

suppose that the materialized cubes will always be

recomputed, but a deferred maintenance technique

can also be used (Mumick et al., 1997). Thus,

maintenance costs (update) of a materialized cube ci

in M are equal to the size of the least ancestor of ci,

or,

(, ) | (, )|iiU c M Lanc c M=

. If u

represents

the frequency of insertions in the base relation, the

total maintenance cost will be

(, )u

UcM

∈

∑

Joining the two former expressions, the total costs

function becomes

(, ) (, )

ii u

icM

qCM f UcM

=∈

∑∑

(4).

This is the cost function that has to be optimized,

being the target of the particle swarm optimization

algorithm that we will describe in the next section. It

is important to notice that update costs may be

computed initially from the base relation and after

from the subcubes that are already materialized.

Then, M in

(, )| (, )|iiU c M Lanc c M=

is initially

empty, being then successively added of the

meanwhile updated subcubes. The same arguments

may be applied if incremental maintenance (Gupta et

al., 1993) is in concern: a generated delta may be

used to compute descendent deltas.

4.2 Problem Coding

In order to apply the particle swarm optimization to

any problem, we must find: 1) a problem coding

plan/scheme in the solutions space; and 2) a fitness

function that may evaluate, in terms of the

objectives, each space position. Once we are

evaluating solutions in a multidimensional space of

multidimensional objects, it seems that the coding is

a direct transpose. Each subcube may or may not be

materialized, showing that a binary coding is the

elected one, what implies, at least a priori, the use of

the discrete PSO (DPSO), where the space is [0,1]

for each dimension. Moreover, the use of the

continuous-discretized version of PSO was also

attempted, but it came across a serious problem,

very hard to solve, since the particles left the

possible/authorized solution space, and some

solutions attempted were not effective. We will have

as many dimensions as possible subcubes in the

OLAP cube, which is to say, as many dimensions as

the bits that represent each solution.

Figure 1: Data cube Lattice.

Based on the example of the data cube presented

in Figure 1, with dimensions customer, product and

supplier, we will have 8 possible subcubes, and

consequently 8 dimensions. The distribution scenery

1 (Figure 2) will be (00111101) in the binary form,

which corresponds to the location of the particle in

point (0,0,1,1,1,1,0,1). In figure 2 a view of this

mapping is shown, restricted to 3 subcubes, and

concerning to two different OLAP subcube

distribution sceneries.

Figure 2: Cube materializing mapping in DPSO

multidimensional.

The fitness function estimates the “fitness”

degree of the solution, in terms of objective

satisfaction. Each particle in the swarm is evaluated,

being its fitness determined by its respective position

in the DPSO space. Each location matches a certain

solution whose value is evaluated by the fitness

function. If the location is good enough, it will

become another pbest or gbest position, what pushes

the other particles towards it. In our case, the cost

A DISCRETE PARTICLE SWARM ALGORITHM FOR OLAP DATA CUBE SELECTION

function of equation 4, will be used as adaptation

function, since it determines the fitness of the

solution during the pursuing of the different goals.

As equation 4 is a cost, we aim at its minimization,

which means that the particle with the lower cost is

the one with a bigger fitness.

4.3 The ODCS-DPSO Algorithm

Algorithm 1 shows the basic form of the proposed

OLAP Data Cube Selection DPSO algorithm that is

based on the standard discrete particle swarm

algorithm. The fitness function is the cost computed

using equation 4, and M is the solution proposed by

the position of each of the swarm’s particles,

according to the mapping described previously in

section 4.2.

Algorithm 1: OLAP data cube selection discrete particle

swarm (ODCS-DPSO) algorithm.

4.4 Dealing with Impossible

Solutions

The wandering of the particles through the PSO

space leads, inevitably, to impossible solutions. The

question resides in the fact that the PSO search

algorithm does not include a space constraint in its

coding scheme. To avoid this situation, we can

correct the wrong particle, choosing between

different solutions. Some of them are proposed in

the genetic algorithms domain: 1) randomly, to

eliminate subcubes until the constraint is met; 2)

using a scheme of successive elimination of

subcubes (similar to the former), but not in a random

way: the subcubes are eliminated in a way that the

solution is the less damaging for the cube’s

adaptation (a little like a repair); 3) applying a

constant or adaptive penalty, proportional to the

seriousness of the violation (in this case, the excess

relatively to the imposed space constraint); 4)

leading the “fault” particle to the location of a more

adapted one (e.g. gbest), keeping, nevertheless, the

particle’s pbest, what settles an only partial

substitution (this solution may be considered as an

hybridization with the genetic algorithm), where the

wrong particle is simply substituted; or 5) leading

the research in a way to avoid impossible solutions.

Among these, in this study, we used solution 1. The

others deserve further investigation and are reserved

to future work.

5 EXPERIMENTAL

EVALUATION

Using the cost model, we designed and developed a

query and maintenance costs computing algorithm,

used to implement the fitness function of ODCD-

DPSO. Its formal description is not shown here,

simply due to space constraints. In its design we

included dynamic programming concepts, as the

performance of the algorithms is at premium, given

its intensive use to evaluate the fitness of the

swarm’s particles. Then, we developed an algorithm

that, using, as input, matrixes with the dimensional

hierarchies, parallel hierarchies and composition of

each subcube, generates and makes available the

lattice’s dependencies. This information allows the

easy and fast computing of the least ancestor of any

subcube. All algorithms were implemented in Java.

To the experimental evaluation of the ODCD-DPSO

algorithm we accomplished a set of tests, namely, to

estimate the fitness of the solutions, the quickness in

achieving good ones and its scalarity. For test data,

we have used the test set of Benchmark’s (TPC-R),

selecting the smallest database (1 GB), from which

we selected 3 dimensions (customer, product and

supplier). To broaden the variety of subcubes, we

1. Initialization: randomly initialize a population of particles

(position and velocity) in the n-dimensional space.

{}

Miyx ii ,...,1,, =

[]

x 1,0∈

and

[]

vvv maxmax,−∈

;

Deal with invalid particles as 2.4.

All positions

iipbest

←,

;

iter←0;

2. Population loop:

For each particle, Do:

2.1. Own goodness evaluation and pbest update:

// evaluate the ‘goodness’ of the particle

)()( , ipbestadaptiadapt xfxf > then

iipbest

←, ; // update pbest, if the goodness of

// the particle > its best goodness so far

2.2. Global goodness evaluation and gbest update:

)()( , gbestadaptipbestadapt xfxf > then

ipbestgbest

,←

; // update gbest if the goodness

// of this particle > the goodness that any particle

// has ever achieved

2.3. Apply rules of DPSO: apply eq. (2), rule (3) and (1);

2.4. Deal with invalid particles: // if the storage space of

// subcubes’ solution > available materializing space

Uses one of the methods described in section 4.4;

iter++;

3. Cycle: Repeat Step 2 Until iter== user defined number of

iterations.

4. Return: M, corresponding to the best achieved position of

any swarm’s particle.

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

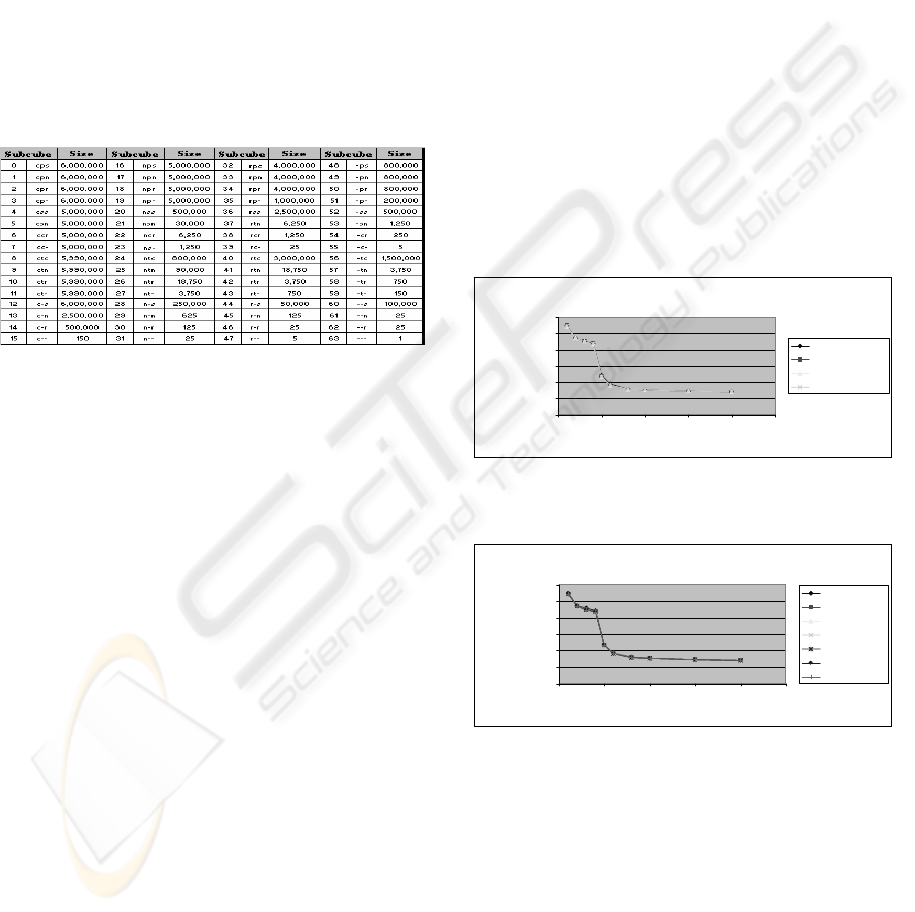
added additional attributes to each dimension,

forming the hierarchies: customer: c-n-r-all;

product: p-t-all and p-s-all; supplier: s-n-r-all. It is

important to emphasize that one of the dimensions

(product) shows parallel hierarchies: this way, the

algorithm implementation should bear this

characteristic. As we have 3 dimensions, with 4

hierarchies each, we will have a total of 64 (4x4x4)

possible subcubes (Table 1), jointly with their sizes

(in tuples). We’ll also suppose that the query (or

maintenance) costs, when the base relation is used,

are of 18 M tuples (3 times the cost of subcube cps)

and that the materializing frequency is 0.1.

Table 1: Generated subcubes with described dimensions

and hierarchies and corresponding size (in tuples).

In the following tests, we shall determine the impact

of the variation of some parameters over the

querying and maintenance costs. Firstly, two of them

will be analyzed: the frequency of the subcubes

utilization and the space available for the cube

materialization. As for the first, the algorithms have

been tested to a uniform, random and with an

inverse linear variation of the respective size

frequency distribution. All the queries’ frequencies

have been normalized to complete a total of 64

queries. Now, in the second parameter, we have

selected percentages 1, 2, 3, 4, 5, 6, 8, 10, 15, 20 %

of the maximal cube size (corresponding this to an

integral maintenance, the sum of the size of all

possible subcubes). With comparative proposes, we

also design and implement a greedy algorithm, a

variation of the one described in (Harinarayan et al.

1996), including on the benefit metric the usage

frequency of each subcube, considering both the

querying and maintenance costs and a materializing

space constraint.

Concerning to ODCD-DPSO parameters, in the

beginning, the particle generation is random and the

way for the algorithm to deal with the location of the

invalid particles is random, which means that if a

particle proposes a cube that exceeds its maximal

size, a random elimination of the subcubes is

pursued, until the constraint is met. Vmax = 10 and

w linearly varies from 0.99 to 1 with the iterations’

number. As soon as we carried out the first

experiment, we understood how easily the ODCD-

DPSO converged, even with the random way to deal

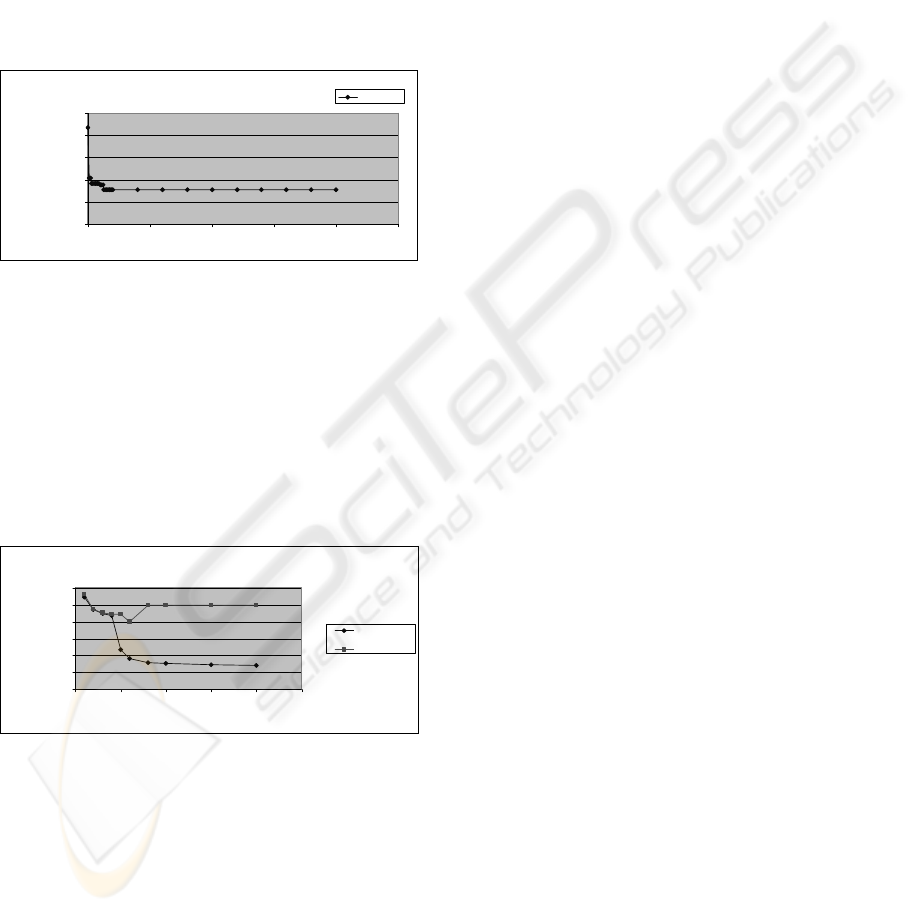
with the invalid solutions. Figures 3 and 4 show the

impact of the maximal number of iterations allowed

and the number of particles in the swarm on the total

costs of the solution achieved. It is clear that the

impact of both parameters in the quality of the

solution is residual. Even with 5 particles or 20

iterations the solutions have a decrease of 3% on the

total costs of the solutions achieved. That is in

accordance with what is said in (Shi & Eberhart,

1999), where it is shown that the standard PSO

algorithm with different population sizes shows an

almost equal performance. The graphs show also an

important decrease of the costs until percentages of

10% of the materializing space; beyond the 10%, the

gain is almost null, due to the progressive impact of

the materializing costs (as probably the new

subcubes are almost redundant ones).

Impact of the Iteration Number on the Total Costs

0,0

100.000.000,0

200.000.000,0

300.000.000,0

400.000.000,0

500.000.000,0

600.000.000,0

0 5 10 15 20 25

Maximal Materializing Space

Total Costs (in tuples)

TotalCosts_100iter

TotalCosts_200iter

TotalCosts_500iter

TotalCosts_1000iter

Figure 3: Impact of the number of iterations on the total

costs of the solution achieved with ODCD-DPS algorithm.

Impact of the Number of Particles in the Swarm on the Total Costs

0,0

100.000.000,0

200.000.000,0

300.000.000,0

400.000.000,0

500.000.000,0

600.000.000,0

0 5 10 15 20 25

Maximal Materializing Space

Total Costs (in tuples)

TotalCosts_5p

TotalCosts_10p

TotalCosts_20p

TotalCosts_50p

TotalCosts_100p

TotalCosts_200p

TotalCosts_500p

Figure 4: Impact of the number of the particles in the

swarm on the total costs of the solution achieved with

ODCD-DPS algorithm.

Concerning to the algorithm’s performance, the test

shows an increase of the run-time with the number

of particles (e.g. 200 iterations with 5 particles in 3.4

seconds x 200 iterations with 500 particles in 25

seconds), but the increase is not of the same ratio of

the number of particles (an increase of 100x on the

particle number, implied an increase of 7x on the

run-time). That is a characteristic that in the test case

A DISCRETE PARTICLE SWARM ALGORITHM FOR OLAP DATA CUBE SELECTION

was not relevant (as the evidenced reduced impact of

the number of particles in the swarm on the quality

of the solution), but that in a real DW system (of

higher complexity) may be interesting. Other set of

tests used a uniform query frequency and the results

confirmed the behaviour evidenced above.

We also tested the evolution of the quality of the

solution achieved with the number of iterations

(Figure 5). We used a 100 swarm particles and a

10% materializing space. The graph shows an

extreme speed of the algorithm search for good

solutions.

Fitness Evolution of ODCD-DPSO Algorithm

100.000.000

200.000.000

300.000.000

400.000.000

500.000.000

0 50 100 150 200 250

Iteration

Total Costs (in

tuples)

TotalCosts

Figure 5: Best fitness x number of iterations of a 100

particles in the swarm and 10% materializing space.

The final test was the comparative performance analysis of

ODCD-DPSO and greedy algorithms (Figure 6). We can

see a consistent better performance of the former

algorithm (marginal to materializing spaces till 4 %) but

clear from 5% and above). Especially in the [5-10%]

range, the ODCD-DPSO is clearly better, very interesting

in real DW, where the materializing cube has to be

restricted to percents of that kind.

Comparative Analysis of ODCD-DPSO and Greedy Algorithms

100000000

200000000

300000000

400000000

500000000

600000000

0 5 10 15 20 25

Maximal Materializing Space

Total Costs (in tuples)

ODCD-DPSO

Algorithm

Greed

Figure 6: Comparison of greedy selection and

ODCD-DPSO algorithms with random query frequencies.

6 CONCLUSIONS AND FUTURE

WORK

In this article, we proposed a subcube selection

model from a data cube that uses a discrete particle

swarm optimization algorithm. The experimental

evaluation performed seems to demonstrate the

effectiveness of the application of DPSO to the cube

selection problem, given a certain queries profile

and a space constraint, seeking to minimize at the

same time the maintenance and querying costs of the

cube. More than a good performance, the PSO had

no difficulty in achieving good and solid results. It

evidenced also a good scalability, as the run-time is

linear with the swarm’s particles number (with low

slope) and the number of selected particles has also a

reduced impact on the run-time (e.g. 13 subcubes on

17.7 seconds x 36 subcubes on 25.9 seconds). Also,

we saw that the algorithm with a low number of

particles in the swarm and reduced number of

iterations achieved immediately good solutions.

Those evidences show a high “power reserve” of the

algorithm to deal with high complexity cube

schemas. We also referred the enormous range of

variations that can be introduced to the base

algorithm, that show already some interesting

results, but that deserve a deeper investigation for

each case. The most important is the domain of the

hybridization, e.g. the solution for the repair of the

gain loss implemented, since it uses DPSO and an

inverse greedy algorithm. In this domain, there are

several other alternatives, because, as referred in

(Kennedy & Eberhart, 1997) the PSO does not have

a mechanism that allows catastrophic jumps from

one region to another, once, unlike the genetic

algorithms, the particle swarm keeps a memory of

the past successes and tends to converge to research

space regions where once were achieved successes.

The genetic combination that occurs in the crossings

will allow those jumps. This way, some changes are

occurring to the algorithm, in search for the

improvement of the solutions. Among them, in a

future work, the next will be attempted: to

implement a minimum for genetic hybridization to

deal with the invalid solutions, forcing them to

retreat to pbest or make it to gbest; a more spreaded

hybridization, what can be considered as a large

scale mutation, promoting the particle’s substitution

for the more adapted ones, a solution proposed in

(Angeline, 1998) with very promising results; and a

deeper degree of genetic hybridization, that

implements the crossing operator, proposed in

(Lǿvbjerg et al. 2001).

Besides the hybridization, other techniques come

to scene, namely: to seek to direct the particle’s

dynamic in a way that invalid solutions would be

avoided, what would also prevent the disturbances

caused by the subsequent recuperation mechanism (

something as assuming a pro-active attitude); and to

try to use all kinds of variants to the original PSO in

the discrete PSO, specially the cooperation

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

mechanism between particle swarms, properly called

particle swarm cooperative optimizer, described in

(Van den Bergh & Engelbrecht, 2004).

ACKNOWLEDGMENTS

The work of Jorge Loureiro was supported by a

grant from PRODEP III, acção 5.3 – Formação

Avançada no Ensino Superior, Concurso N.º

02/PRODEP/2003.

REFERENCES

Angeline, P., 1998. Using Selection to Improve Particle

Swarm Optimization. In Proc. Of the IEEE

International Conference on Evolutionary

Computation (ICEC’98), Anchorage, Alaska, USA,

May 4-9.

Baralis, E., Paraboschi, S., and Teniente, E., 1997.

Materialized View Selection in a Multidimensional

Database. In Proceedings of the 23rd International

Conference on Very Large Data Base (VLDB),

Athens, Greece, pp. 156-165.

Codd, E.F., Codd, S.B., and Sulley, C.T., 1993. Providing

OLAP (On-Line Analytical Processing) to User

Analysts: An IT Mandate. Technical Report.

Chaudhuri, S. & Dayal, U., 1997. An Overview of Data

Warehouse and OLAP Technology. In ACM SIGMOD

Record 26(1), pp. 65-74.

Eberhart, R.C., & Kennedy, J., 1995. A new Optimizer

Using Particle Swarm Theory. In Proc. Os the Sixth

International Symposium on Micro Machine and

Human Science, Nagoya, Japan, IEEE Service Center,

Piscataway, NJ, pp. 39-43.

Gupta, A., Mumick, T., and Subrahmanian, V., 1993.

Maintaining Views Incrementally. In Proceedings of

ACM SIGMOD 1993 International Conference on

Management of Data, Washington, DC.

Gupta, H., Harinarayan, V., Rajaraman, A., and Ullman,

J., 1997. Index Selection for OLAP. In Proceedings of

the Intl. Conf. on Data Engineering, Birmingham, UK,

pp. 208-219.

Gupta, H., 1997. Selection of Views to Materialize in a

Data Warehouse. In Proceedings of ICDT, Delphi, pp.

98-112.

Gupta, H. & Mumick, I.S., 1999. Selection of Views to

Materialize under a Maintenance-Time Constraint. In

Proc. Of the International Conference on Database

Theory.

Harinarayan, V., Rajaraman, A., and Ullman, J., 1996.

Implementing Data Cubes Efficiently. In Proc. of

ACM SIGMOD, Montreal, Canada, pp. 205-216.

Horng, J.T., Chang, Y.J., Liu, B.J., and Kao, C.Y., 1999.

Materialized View Selection Using Genetic

Algorithms in a Data Warehouse. In Proceedings of

World Congress on Evolutionary Computation,

Washington D.C.

Kalnis, P., Mamoulis, N., and D. Papadias, 2002. View

Selection Using Randomized Search. In Data

Knowledge Engineering, vol. 42, number 1, pp. 89-

111.

Kennedy, J., & Eberhart, R.C., 1995. Particle Swarm

Optimization. In Proc. of IEEE Intl. Conference on

Neural Networks (Perth, Australia), IEEE Service

Center, Piscataway, NJ (1995) IV:1942-1948.

Kennedy, J., and Eberhart, R.C., 1997. A Discrete Binary

Version of the Particle Swarm Optimization

Algorithm. In Proc. of the 1997 Conference on

Systems, Man and Cybernetics (SMC’97), pp. 4104-

4109.

Liang, W., Wang, H., and Orlowska, M.E., 2001.

Materialized View Selection Under the Maintenance

Cost Constraint. In Data and Knowledge Engineering

37(2), pp. 203-216.

Lin, W.-Y., & Kuo, I-C, 2004. A Genetic Selection

Algorithm for OLAP Data Cubes. In Knowledge and

Information Systems, Volume 6, Number 1, Springer-

Verlag London Ltd., pp. 83-102.

Lǿvbjerg, M., Rasmussen, T., and Krink, T., 2001. Hybrid

Particle Swarm Optimization with Breeding and

Subpopulations. In Proceedings of the 3rd Genetic

and Evolutionary Computation Conference (GECCO-

2001).

Mumick, I.S., Quass, D., Mumick, B.S., 1997.

Maintenance of Data Cubes and Summary Tables in a

Warehouse. In Peckham J (ed.). Proceedings of ACM

SIGMOD International Conference on Management of

Data, Tucson, Arizona, pp. 100-111.

Shi, Y., & Eberhart, R., 1999. Empirical Study of Particle

Swarm Optimization. In Proceedings of the 1999

Congress of Evolutionary Computation, vol. 3, IEEE

Press, pp. 1945-1950.

Shukla, A., Deshpande, P.M., and Naughton, J.F., 1998.

Materialized View Selection for Multidimensional

Datasets. In Proc. of VLDB.

Shukla, A., Deshpande, P.M., and Naughton, J.F., 2000.

Materialized View Selection form Multicube Data

Models. In Zaniolo, C., Lockemann P.C., Scholl,

M.H., Torsten, G. (eds.). In Proceedings of Advances

in Database Technology (EDBT’00), Konstanz,

Germany. Lecture Notes in Computer Science 1777,

Springer, Berlin, pp. 269.284.

Transaction Processing Performance Council (TPC): TPC

Benchmark R (decision support) Standard

Specification Revision 2.1.0. tpcr_2.1.0.pdf, available

at http://www.tpc.org

Van den Bergh, F., and Engelbrecht, A.P., 2004. A

Cooperative Approach to Particle Swarm

Optimization. In IEEE Transactions on Evolutionary

Computation, Vol. 8, No. 3, pp. 225-239.

Zhang, C., Yao, X., and Yang, J., 2001. An Evolutionary

Approach to Materialized Views Selection in a Data

Warehouse Environment. In IEEE Trans. on Systems,

Man and Cybernetics, Part C, Vol. 31, N.º 3.

A DISCRETE PARTICLE SWARM ALGORITHM FOR OLAP DATA CUBE SELECTION