Mining Self-similarity in Time Series

Song Meina, Zhan Xiaosu, Song Junde

Beijing University of Posts and Telecommunications,

Xitucheng Road,Beijing, China

Abstract. Self-similarity can successfully characterize and forecast intricate,

non-periodic and chaos time series avoiding the limitation of traditional

methods on LRD (Long-Range Dependence). The potential principals will be

found and the future unknown time series will be forecasted through foregoing

training. Therefore it is important to mine the LRD by self-similarity analysis.

In this paper, mining self-similarity of time series is introduced. And the

practical value can be found from two cases study respectively for season-

variable trend forecast and network traffic.

1 Introduction

The time series is a series of observation data according to time-based sequence

whose value changes with time. The time result is recorded by fixed time interval

which is an important characteristic of time series. It is widely applied in real life for

time series such as the price fluctuation in specified period for stock market, the

arrival time of network service, the birth-rate number for population every year etc.

Time series analysis is that random data series variable with time is analyzed

through probability and statistic methods [1]. Following the continuity principle of all

objects, the future development trend is speculated by statistic analysis based on

history data. This means the following two things. One is that no sudden or jump

movement occurred but progressing with relative short steps. The other is the past and

current phenomena potentially imply the evolution tendency for the future. Therefore

in normal circumstance, the valid result will be achieved for short-term forecast from

time series analysis. To extend into further future there is great limitation for long-

term forecast.

In order to analyze data of time series, the visual inspection tools are used to

record data value and distinguish the characteristics and behaviours of certain

phenomena. For example, to study the increase or decrease direction of the data, the

specific pattern changed with seasons, the related progress should be generated from

proper mathematics model and the forecast analysis is made based on the produced

data.

There are many traditional model for time series analysis, such as ARMA (Auto-

Regression Moving Average) and ARIMA (Auto-Regression Integrated with Moving

Averages). ARMA is a linear model for stationary time series analysis and ARIMA is

widely used for non-stationary series. The common characteristics of the two models

are that the LRD between the values for large time intervals can’t be represented.

Meina S., Xiaosu Z. and Junde S. (2006).

Mining Self-similarity in Time Series.

In Proceedings of the 3rd International Workshop on Computer Supported Activity Coordination, pages 131-136

DOI: 10.5220/0002497501310136

 SciTePress

However the LRD characteristics can’t be neglected. Because the time series

attributes will be changed with cumulative effects[2].

Self-similarity can successfully characterize and forecast intricate, non-periodic

and chaos time series avoiding the limitation of traditional time series analysis on

LRD. The potential principals will be found and the future unknown time series will

be forecasted through foregoing training. Therefore it is important for us to mine the

LRD by self-similarity analysis.

2 Self-similarity in Time Series [3]

If one time series meets the following equation (1), then it is self-similar.

() ( )

yt a y

≡

(1)

Here

≡ suggests that both sides of this equation from the statistical sense are

completely identical. That is to say, after the following transformation，

1）on the X axis, t→t/a

2）on the Y axis,

the distribution function of a self-similar process named y(t) which carried

parameter α still remains unchanged. In this equation the exponent α is called self-

yay

→

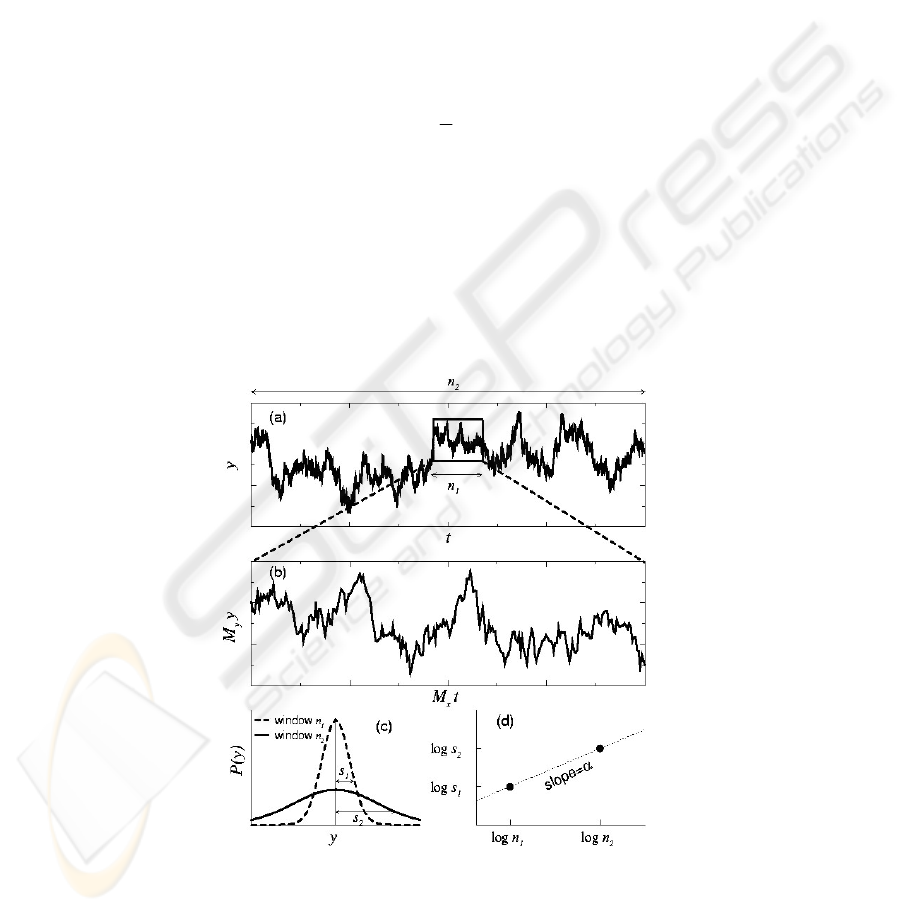
Fig. 1. Self-similarity of a time series.

132

similarity parameter.

However, in fact it is almost impossible to judge whether the two processes

mentioned above are completely identical or not. Because the strict standard requests

that the two processes possess the completely same distribution function, which

means not only the arithmetic mean and variance, but also all the higher order

moments are identical. Thus a relative weakened standard is usually adopted to make

an approximately approached judgment to above equality. That is just checking

whether the average mean and variance, such as first moment and second moment, of

the equation (1) are equal or not.

Fig.1 shows the self-similarity of time series.

(a) A time series with self-similar is shown on the two windows with different

time-scale n

and n

(b) Amplify the smaller window with time-scale n

according to time-scales n

Let’s pay an attention to the two figures in (a) and (b).When the different amplified

multiple M

and M

are adopted respectively in X axis and Y axis, the fluctuation

curves are so close.

respectively from windows in (a). Here s

and s

shows the standard deviation of the

two distribution functions respectively.

(d) The log-log relationship between s and n which is the window size.

The parameter α in equation (1) needs to be abstracted from a given time series.

And the following is the calculation formula.

α=lnM

ln M

(2)

The following equation (3) will be created when put the two parameters M

，

into the corresponding position in the equation (2)

(3)

In order to analyze the self-similarity characteristic of given time series, the

following steps should be done.

1) Divide any given observation window into many same size and independent

subsets. To achieve the more reliable value, the average of s in the all subsets

should be calculated.

2) Repeat the above process continually. Then draw these s-n couples on the log-

log plot to estimate the self-similarity parameter α.

The method described above can be no more than applied to certain non-

stationary time series, especially to these with slow movement trend. This means not

all non-stable time series can be well handled with this method. Concerning the self-

similarity parameter, which is also named the Hurst parameter, of most of non-

stationary time series can be precisely estimated through Whittle Estimator method,

which is the practical application of maximal possibility method[4][5]. Whittle

Estimator can provide the confidence interval of the Hurst parameter.

Take the FGN (fractional Gaussian Noise) for example to show the application

of Whittle Estimator in the Hurst parameter estimation. If the data derive from the

FGN procession, the estimated value of Hurst can be gained through minimizing the

value of function Q (H). In the following equation (4), the H is equal to α

mentioned above.

lnln

−

133

(4)

Therein

)(

is the estimated value of a spectral density got out through

Fourier series transformation on time period N, which is defined in the discrete time {

, t=0,1,2,3……}by a random process X(t).

(5)

),( HS

in (6) is the spectral density.

S(ω,H

)≈

|ω|

1-2H

ω → 0

(6)

The estimated value of C

is shown in (7).

∑

−

)(1



(7)

So for the discrete state, equation (8) comes into existence.

)log(

)(

jHf

−

∑



(8)

An equation (9) will be built by putting the value of function (7) into the right

location in function (8).

∑

−

++=

)log(

)21(

)

)(

log(1)(

(9)

Therein the value of ω

can be 2π/N,4π/N,…, 2π.

In this way, the value of Hurst parameter can be estimated through minimizing

the value of equation (9).

3 Self-similarity Applied in Data Mining

The data mining of time series, specifically, implies that the useful information can be

got in the database composed of time-based sequence or event whose value changes

with time. It includes trend analysis, similarity query, mining of sequential patterns

and periodic-mode mining [6].

3.1 Self-similarity Applied in Trend Analysis

The long-term trend change of time-based sequence reflects a kind of trend curve

during a relative longer time interval. Given a group of fixed data{x

, t=0,1,2

…}, the

ωωω

dHSd

∫∫

−−

+= ),(

),(

)(

∑

134

normal methods deciding sequence trend can be used to calculate n-order moving

average according to the following arithmetic mean equation sequence.

(10)

Smoothness of time series by moving average can decrease the abnormal

fluctuation, which deviates from the original sequence. After that, in equation (10),

the right n-order weighted average made by adopting weighted average can reduce the

influence of the extreme data on sequential trend of the whole time series. The trend

curve can also be got though curve fitting by least square method.

Both methods mentioned above can not find the LRD characteristic. The time

series, whose value changes with seasons, is the typical ones with long-range

dependency. The season-variable time series indicates that there is an identical or

almost identical mode which appears repeatedly in the special months of the several

consecutive years. For example, dramatic traffic increasing during Spring Festival is

an almost identical mode for statistical data based on every year. Long-range

dependency is an inherent attribute for self-similarity. In order to analyze the long-

range dependency trend, self-similarity method should be introduced. In general, the

season-variable time series forecast methods can be described as followings.

3) Based on the self-similarity analysis on time series from the previous years, the

Hurst parameter will be created. And consequently the principal trend for the

whole time series can be built.

4) Combined with the traffic increasing of current recorded year, let’s just make the

corresponding amplitude shift. Then the rough trend curve will be presented with

season change.

Thus traffic forecast analysis will be made for long-term traffic.

3.2 Self-similarity Applied in Mining Network Traffic

Self-similarity is an important character of web traffic [7]. That means it is always

possible for the larger peak period occurs. In order to mine the behaviour pattern on

different time scales, traditional methods can’t capture the most distinct

characteristics of the web traffic. Therefore self-similarity analysis must be made to

mine the recorded time series on different time scales.

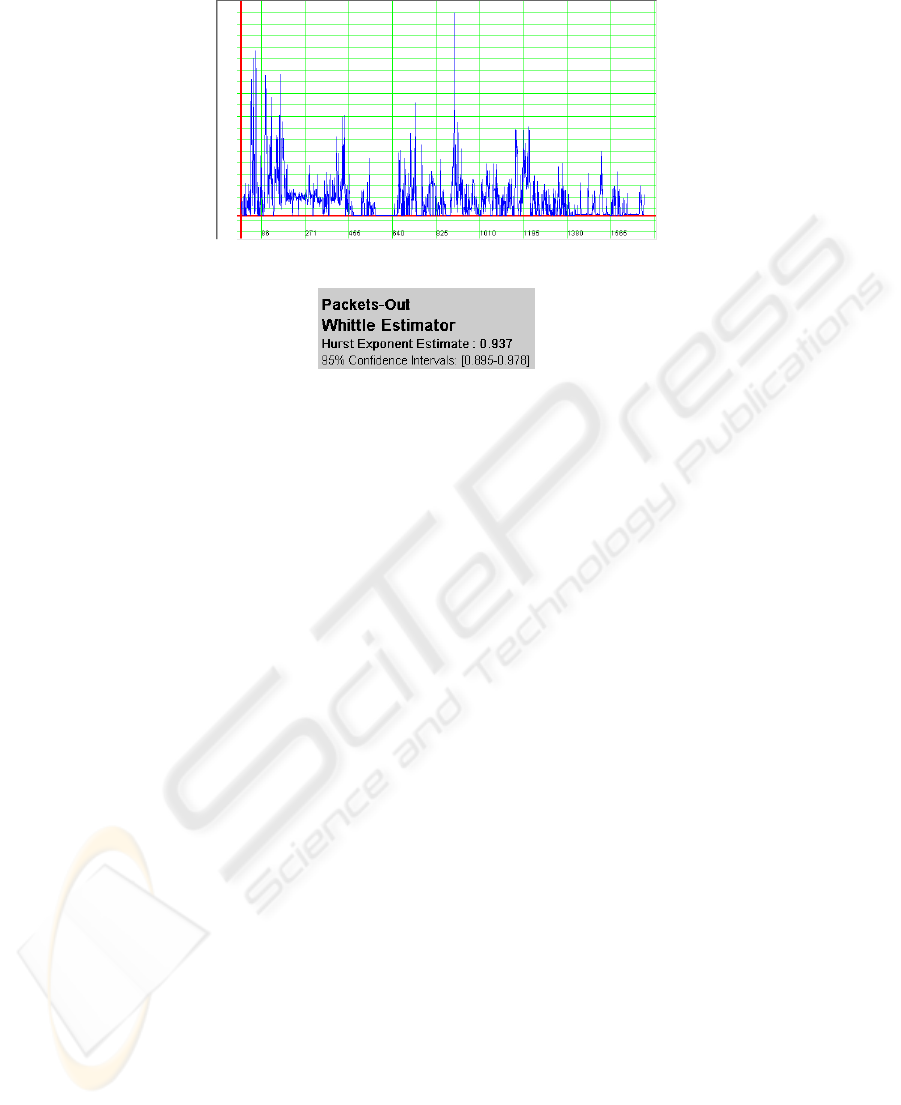
Figure 2 is the collected data from China Mobile, which represent the number of

packets outputting from VPN (Virtual Private Networks) gateway every 5 minutes

during work-hours. A tool for self-similarity and LRD analysis is designed in [8] and

the Hurst parameter is 0.937 with 95% confidence intervals, which is shown in Figure

From Figure 3, we can observe that the VPN gateway is provided with self-

similarity arrival. So no classical queuing theory can be applied to evaluation the

system performance. For they all suppose the Poisson arrival. This will avoid the

optimal performance estimation of the studied systems.

132

21110

xxx

−

+++

135

4 Conclusions and the Future Works

The traditional methods can get the valid results for short-term forecast from time

series analysis. To extend into further future there is great limitation for long-term

forecast. In this paper, how to do self-similarity analysis on time series is introduced.

Suggestions on applying self-similarity into data mining are put forward. From the

mentioned two cases, both how to forecast time series changed with seasons and how

to mine the behaviour patterns on different time scales are discussed. The detailed

implementation will be studied in the further research.

References

1. G.E.P Box and G.M.Jenkins, 1976. Time Series analysis: forecasting and control. 2nd

Edition, Holden_Day, San Francisco.

2. Feder J, 1988. Fractals. New York: Plenum Press.

3. Beran J, 1994. Statistics for Long-Memory Processes. New York: Chapman & Hall.

4. S. Molnár, T. D. Dang, A. Vidács, 1999. Heavy-Tailedness, Long-Range Dependence and

Self-similarity in Data Traffic. 7th International Conference on Telecommunication

Systems Modeling and Analysis, Nashville, Tennessee, USA.

5. Lin Chuang

， 2001. Performance Analysis on Computer Networks and Computer

Systems.Tsing Hua Press.

6. Jiawei Han,Micheline Kamber, 2001. Data Ming: Concepts and Technoloties. China

Machine Press.

7. M.Crovella, A.Bestavros, 1997. Self-similarity in World Wide Web Traffic: Evidence and

Possible Causes.IEEE/ACM Transactions on Networking,5(6):835-846.

8. Thomas Karagiannis, Michalis Faloutsos, 2005. The SELFIS Tool.

http://www.cs.ucr.edu/~tkarag/Selfis/Selfis.html

2500

5500

7500

10000

12500

Fig. 2. Packet Number of the VPN Gateway

Fig. 3. Hurst Parameter

136