Toward a Pi-Calculus Based Veriﬁcation Tool for Web

Services Orchestrations

Faisal Abouzaid

Ecole Polytechnique de Montreal,

2500-chemin de Polytechnique,

Montreal (Quebec) H3T 1J4 , Canada

Abstract. Web services constitute a dynamic ﬁeld of research about technolo-

gies of the Internet. WS-BPEL 2.0, is in the way for becoming a standard for

deﬁning Web services orchestration. To check the good behaviour of the pro-

duced compositions, but also to check equivalence between services, formaliza-

tion is necessary. In this paper a contribution to the ﬁeld of Formal Veriﬁcation

of Web services composition is presented using a πcalculus-based approach for

the veriﬁcation of composite Web services by applying model checking methods.

We adopt the possibility of exploiting beneﬁts from existing works by translating

a Business Process Language such as BPEL to a system model of the π-calculus

for which analysis and veriﬁcation techniques have already been well established

and there are existing tools for model checking systems. We therefore present

the basis of a framework aimed to speciﬁcation and veriﬁcation, related to some

temporal logic, of Web services composition. . ..

1 Introduction

Web services are a typical example of technologies supporting Service Oriented Ar-

chitectures (SOA). They allow to develop applications taking advantage of the Internet

infrastructure. These distributed applications communicate by messages and use stan-

dardized protocols all based on XML. These Web services can be composed to form

more complex applications. Such a composition is called an orchestration, if there is

a coordinator between interacting services, and a choreography if not. These new con-

cepts raise some challenges: How to be sure that a composite Web service works cor-

rectly? How to make sure that two or several Web service interact correctly and that

the result of the interaction is acceptable in comparison with the initial speciﬁcation?

How to make sure that two services are compatible so that one can substitute them one

for the other, where necessary? To answer these question a formal speciﬁcation of the

compositions is needed and justiﬁed by the need for developing reliable services which

fulﬁll the requirements of the users.

These problems are not recent, nor speciﬁc to Web services. Techniques and many

tools exist which make it possible to specify formally and to check properties on var-

ious systems. However, Web services have particular characteristics which require to

be studied speciﬁcally. For example, concerning the composition of Web services, a

service can dynamically establish a transaction with a service whose behavior is not

Abouzaid F. (2006).

Toward a Pi-Calculus Based Veriﬁcation Tool for Web Services Orchestrations.

In Proceedings of the 3rd International Workshop on Computer Suppor ted Activity Coordination, pages 23-34

DOI: 10.5220/0002501900230034

 SciTePress

known in advance. An abstract representation of the behaviors of all the participants,

in an adequate formalism, can help to reason in an automatic way. In the same way the

formalism can help to design a reliable automatic composition of services. On another

side, mobility is essential in the world of Web services : a service can communicate with

customers whose address is not known in advance, but discovered during the execution.

Some formalisms do not make it possible to express it correctly, the π-calculus does.

In this work we study the problem of formally design Web Services compositions

expressed by means of a BPM language such as BPEL, using π-calculus. We compare

different formalism and show that process algebras and in particular π-calculus, are well

suited for the purpose of formally specifying such compositions. We aim to provide a

thoerotical and concrete framework to design and formally verify Web Services compo-

sitions. Our purpose is to develop a framework dedicated to veriﬁcation and design of

robust and complex Web services that is based on π-calculus formalism. The ﬁrst step in

this way is to provide a π -based semantics for Web services orchestrations expressed by

the means of BPEL, which seems to be the most popular BPM language. Based on this

semantics, we propose a mapping between main BPEL constructs and π-calculus. We

present the π-logic, an extension of the µ-logic, associated with π-calculus that allows

us to express properties we want to verify. We illustrate our method by a signiﬁcative

example. Finally we present a basic architecture for our veriﬁcation framework based

on model-checking of this formalism.

In this paper, we will proceed in the following way: after having introduced Web

services and their compositions in section two, we justify the need for formalization in

section three, and we brieﬂy discuss various formalisms used for this purpose. We then

highlight the fact that process algebras are well suited for Web services formalization. In

Section four, a brief presentation of the syntax and semantics of the π-calculus is given.

The π-logic is also presented. In section ﬁve we present a mapping guide from BPEL

to π-calculus and we show its relevance with a concrete example. In section six we

discuss fundamental basis for a framework dedicated to formalization and veriﬁcation

of composite Web services. In section seven we conclude our presentation by reporting

some conclusive remarks and a summary of the works. We also give and some hints for

future works.

2 Web Services

A Web service is an application provided by a service provider running on the internet

and accessible to the customers through standard internet protocols. The W3C consor-

tium deﬁnes a Web service as an application or a component that is identiﬁed by an

URI and whose interfaces and links are described in WSDL, an XML-based language.

Deﬁnitions of Web services can be discovered by other services by means of the UDDI

protocol and they can interact directly with other services by using XML language and

SOAP protocol.

2.1 Orchestration and Choreography Languages

Because each service provides a limited functionnality, it is then necessary to compose

these basic Web services in order to build a more complex composite service, providing

a fonctionnality of higher level of abstraction in order to reduce development costs, to

provide strong reactivity to customers requests, and scale economies.

Several communities act in production of standard languages to describe speciﬁ-

cations of orchestration but we focus our work on the language which seems to join

together around him greater unanimity, namely BPEL (in the past BPEL4WS) [1]. This

language supported by IBM and Microsoft, is in the way to become a standard. It is

a programming language for implementing the execution logic of a business process

based on interactions between the process and its partners. A BPEL process deﬁnes

how multiple service interactions with partners are coordinated internally to achieve a

business goal (orchestration).

While orchestration depends on a coordinating service, choreography is concerned

with global, multiparty peer-to-peer collaborations interoperable between any type of

components. WS-CDL is a language in which a choreography description is speci-

ﬁed[2]. A WS-CDL speciﬁcation describes the observable behavior of collaborations

between services. WS-CDL is not a programming language; it is not executable.

3 Formalization of Web Services Orchestrations

3.1 Formalization

Formalization of composite Web services is justiﬁed by the need for the checking prop-

erties which attest the correct behavior of the whole system. Many works are devoted to

the ﬁeld of modeling and verifying Web services and their composition. An approach

to process behaviour analysis and modelling of these software architectures can be con-

structed to provide tools for veriﬁcation and validation of speciﬁed properties of the

model against design speciﬁcations and implementations.,

Various researches concerning Web services composition and based on various for-

malisms were proposed among such as Petri Nets [3], ASM (Abstract State Machines)

[4], Automata with guards [5] or CCS [6].

3.2 Formalisms

Abstract State Machines. The interest of the ASM lies in their expressivity and their

simplicity. They make it possible to conceive achievable speciﬁcations that makes it

possible to check directly on the model. However, this technique is not adapted to ap-

plications that process lot of data and it is the case of Web service which can exchange

very signiﬁcant volumes of information.

Petri Nets. Petri nets make it possible to model events and states in a distributed sys-

tem. They make it possible to simply express sequentiality, concurency and asynchro-

nous control based on events. They present some advantages for worﬂow modeling such

as offering a formal semantics, though graphic. Other advantages are that their seman-

tics is based on states and not only on events and there exist lot of tools for analysis.

However, Petri nets are not free from problems [7]. Thus certain difﬁculties ap-

pear with usage such as difﬁcult to represent multiple instances of a sub-process or to

represent some complex synchronization patterns (cancellation pattern (cleaner) ).

Process Algebras. Most of the problems raised by the previous techniques ﬁnd their

solution by using process algebras. They are used in various domains, thanks to their

great capacity of modeling and to their relative simplicity of writing. They make it

possible to describe the evolution and the behavior of realizable interactions within

concurrent systems and they often are represented by programming languages reduced

to a simple expression. [8]

They are suitable to describe Web services, because they offer a formal description

of dynamic processes, which facilitates their automatic veriﬁcation. They allow a great

expressivity and provide constructions that are adapted to composition because they

have compositional properties, Finally their textual notation is adapted to the descrip-

tion of real size problems , although it is less readable than transitions systems.

Process algebras are useful both at the time of design and for ’reverse engineering’.

They offer the possibility of automatically generating skeletons of code thanks to a

translation from the algebra to an executable language.

CCS. The Calculus of Communicating Systems [9] is a calculus for describing sta-

tic networks of processes that synchronize via channels. CCS doesn’t allow to pass

channel-names as arguments while the main advantage of π-calculus is that it does.

4 The π-calculus

4.1 Introduction

The π-calculus [10], is a process algebra that can describe mobile concurrent compu-

tation in an abstract way. It provides a way to deﬁne labelled transition systems which

can exchange communication channels as messages. Name communication, together

with the possibility of declaring and exporting local names (scope extrusion), gives this

calculus a great expressive power.

4.2 The π-calculus Syntax

We refer to [10] for a detailed description of the π-calculus, but we will give here a brief

introduction to its syntax.

The π-calculus consists of a set N of names (for actions) and action preﬁxes α that

are a generalization of actions. An action preﬁx represents either sending or receiving

a message (a name), or making a silent transition (τ ). Actions syntax and the set of

π-calculus process expressions are given in Table 1.

The meaning of each process deﬁned above is as follows :

Null: 0 is the deadlocked process which cannot involve with any transition.

Preﬁxed sum:

i∈I

can proceed to P

by taking the transition of the action preﬁx

: Transitions and nondeterministic choices are described as preﬁxed sums.

Parallel composition: P

| P

is a process consisting of P

and P

which will operate

concurrently, but may interact with each other through actions/co-actions.

Restriction: (νa)P means that the action/co-action a or

a in P can neither be observed

outside, nor react with a or a outside the scope of P .

Table 1. π-calculus Actions and Process syntax.

Action syntax Process syntax

P ::= x(y) receive y along x P := 0 (null)

xhyi send y along x |

i∈I

(Preﬁxed sum)

τ silent action | P

| P

(Parallel composition)

| (νa)P (Restriction)

| [x = y]P (Match)

| !P (Replication)

Match: [x = y]P behaves like P if names x and y are identical, and otherwise like 0.

Replication: !P means that the behavior of P can be arbitrarily replicated.

Structural operational semantics of the π-calculus is given by reaction and transition

rules as shown in Table 2.

Table 2. reaction and transition rules of the π-calculus.

T AU : τ.P + M −→ P REACT :

x.hyi.P | x(z).Q −→ P | {y /z}Q

P AR :

P −→ P

′

P |Q −→ P

′

RES :

P −→ P

′

(νx)P −→ (νx)P

′

ST RUCT :

P ≡ P

′

−→ Q

′

Q ≡ Q

′

P −→ P

′

4.3 Model Checking in the π-µ-Calculus

Some logics havebeen proposed [11], [12] to express properties of π-calculus processes.

These logics are extensions, with π-calculus actions, name quantiﬁcations and parame-

terizations, of standard action based logics [13]. The π-logic [14] extends the modal

logic introduced in [11] with some expressive modalities. Its syntax is given by :

Φ ::= true | ∼ Φ | Φ & Φ

′

| EX{µ}Φ | < µ > Φ | EF Φ

The interpretation of the logic formulae is as follows :

– P |= true holds always;

– P |= ∼ Φ if and only if notP |= Φ;

– P |= Φ & Φ

′

if and only if P |= Φ and P |= Φ

′

;

– P |= EX{µ}Φ if and only if there exists P

′

such that P

−→ P

′

and P

′

|= Φ ; This is the

next operator.

– P |=< µ > Φ if and only if there exist P

, ..., P

, n ≥ 1, such that P = P

−→ P

...

−→

n−1

−→ P

and P

|= Φ; This is the weak next operator.

– P |= EF Φ if and only if there exist P

, ..., P

and µ

, ..., µ

, with n 6= 0, such that

P = P

−→ P

...

−−→ P n and P

|= Φ.

Derived operators can be deﬁned like this :

– Φ|Φ

′

stands for ∼ (∼ Φ& ∼ Φ

′

). It is the OR operator;

– AX{µ}Φ stands for ∼ EX{µ} ∼ Φ. This is the dual version of the strong next operator;

– [µ]Φ stands for ∼< µ >∼ Φ. This is the dual version of the weak next operator;

– AGΦ stands for ∼ EF ∼ Φ. This is the always operator, whose meaning is that Φ is true

now and always in the future.

Example of formula: For instance, deadlock freeness can be speciﬁed as follows:

NoDeadLock = AG(< in?∗ > true | < out!∗ > true)

It asserts that every time (always) it is possible to perform an input (on channel in) or

an output (on channel out ), insuring that the system will never block. Note that we use

the HAL syntax (see Section 5.3) which is slightly different from the previous one.

4.4 π-calculus Tools

The main existing tools for model-checking the π-calculus are the ”Mobility Work-

bench (MWB)” [15] and the HAL toolset [14].

MWB is a model-checker for the polyadic π-calculus which allows handling and

analyzis of concurrent mobile systems. It allows checking of bisimulation which can be

very useful for verifying Web services comptability.

HAL is apromising tool which exploits a novel automata-like model which allows

ﬁnite state veriﬁcation of systems speciﬁed in the π-calculus. The HAL environment in-

cludes modules which support veriﬁcation of behavioral properties of π-calculus agents

expressed as formulae of suitable temporal logics.

For our example, we will use the HAL tool, which provides a Web based interface.

5 Mapping BPEL Constructs to π-calculus

5.1 Web Service Composition Operators

Among basic constructions common to the majority of the Web service composition

languages, one ﬁnds the following operations : service invocation (invoke), messages re-

ception (receive), answer (reply), sequenciality (sequence) or parallelism (ﬂow). Mech-

anisms for compensation (compensate), and errors handling (fault handler), are also

used.

Table 3. Mapping BPEL activities to π-calculus.

BPEL π-calculus

Basic Activity

invoke invoke = x

ii | yh ˜ui

< invoke partner=” ” operation=” ” > The channel x

identiﬁes

a speciﬁc operation of a service.

receive

< receive partner=”” operation=”” > receive(x

i = x

(r,

i).yh ˜ui

< reply partner=”” operation”” > reply = x

h˜oi | yh ˜ui

empty

<empty > empty = yh ˜ui

Concurrent Activities

<ﬂow> f low(A

, A

) = (νy

′

)(νy”)(A

′

h˜u

′

i | A

.y”h ˜u”i

< ...activity

... > | y

′

(˜u

′

).y”( ˜u”).yh ˜ui

< ...activity

... >

</ﬂow>

< sequence ... > sequence(A

, A

) = (νy

′

)(A

′

h˜ui | y

′

(˜u).A

)

< ...activity

... >

< ...activity

... >

</sequence>

5.2 Formalization

The ﬁrst step in the formalization process is to map BPEL speciﬁcations into π-calculus

processes. The mapping is required to provide explicit process representation behind

that of the BPEL constructs activities and other process deﬁnitions. The semantics used

here is based on the work presented in [16].

Note that ˜u denotes a set of values a process sends or receives. The π-process core-

sponding to a BPEL process executes an activity and ﬂags out y!˜u to signal its termina-

tion in order to support sequential composition.

It is very natural to map basic construct from BPEL to π-calculus. Thereby, an

invoke or a reply statement will be translated using an output action while a

receivestatement will be translated to an input action. A flow activity will be trans-

lated using a parallel composition operator. A sequence activity can be translated

using a parallel or a preﬁxed operator (see Table 3 for the mapping).

Note that ˜u denotes a set of values a process sends or receives. The π-process core-

sponding to a BPEL process executes an activity and ﬂags out y!˜u to signal its termina-

tion in order to support sequential composition.

A while construct can be expressed by means of a replication action, or by using

recursion and a switch construct is mapped using a Match action. A pick construct

is mapped by means of a preﬁxed sum action (see Table 4 )..

The mapping presented here is limited to some usual constructs. We refer to [16] for

a detailed speciﬁcation of fault handling and scope speciﬁcation. More com-

plex patterns from the world of workﬂow have been translated but not presented here.

5.3 An Example

In order to illustrate the use of the π - calculus and the HAL tool on a concrete way, we

present the simple example of a company which receives from a customer information

about an order. The company treats the order and then transmits it to the supplier who

in his turn reply by sending information on the delivery. the company will retransmit

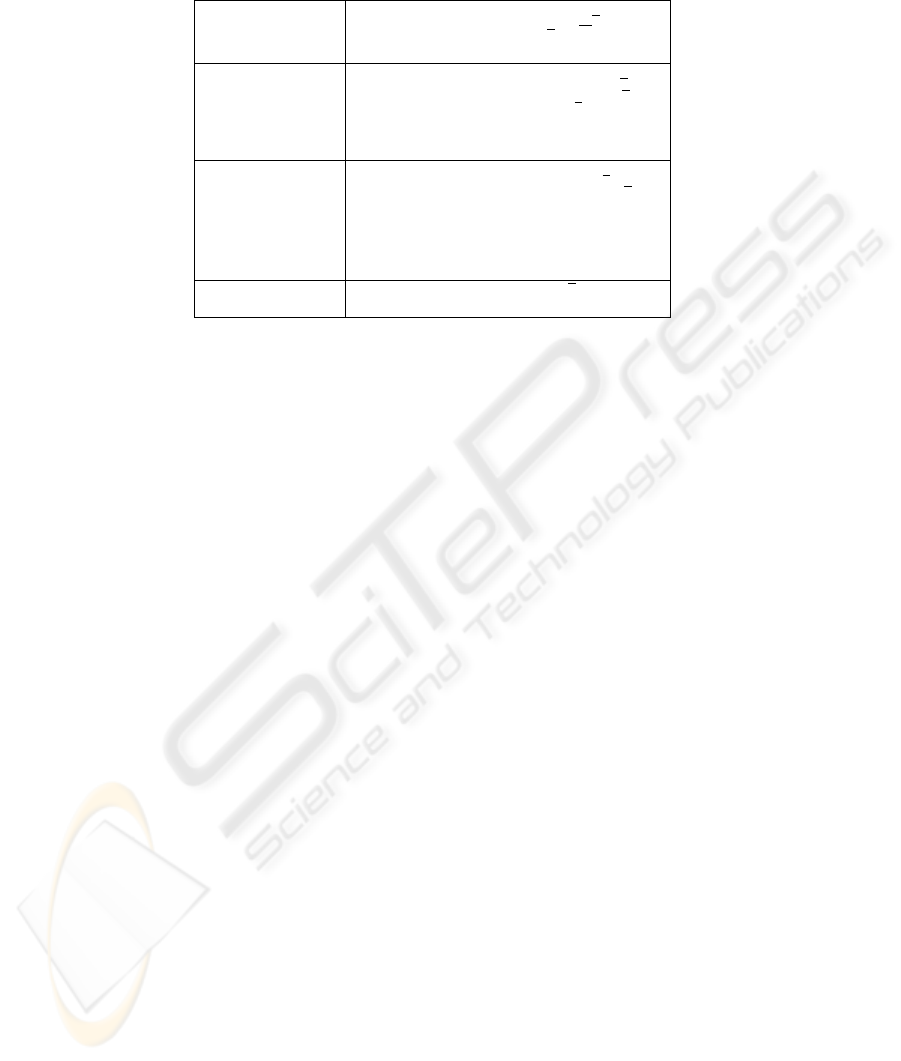
Table 4. mapping BPEL structured activities to π-calculus.

<while condition =”exp = ’yes’”> while(cond, A

) = (νy)(y(˜v)

<sequence> | [cond].yh˜vi.while()

< ...activity

... > | yh˜vi.y

′

h˜ui)

</sequence>

</while>

<case condition=” ”> switch(x, A

, ..., A

) = [x = a

.yh ˜ui

< ...activity

... > | [x = a

.yh ˜ui

</case> | A

.yh ˜ui

< ...activity

... >

</otherwise>

</switch>

<pick > pick((x

, i

, A), (x

, i

, A)) =

standard-elements x

.yh ˜ui

<onMessage partnerLink=” ” >+ + x

.yh ˜ui

operation=” ” >+

<correlations>?

<correlation set=” ” >+ x

: channel for a speciﬁc service

</correlations>

activity

</onMessage>

</pick>

<compensationHandler> compensate = z!o | yh˜ui

< ...activity

... >

</compensationHandler>

these information to its customer. This company must thus deﬁne and document the

trade process which it must implement.

We thus have 3 services that interact : A buyer who sends a purchase order number

and a credit card number to the company. He receives in response a delivery date at

his address. A seller (the company) receives the purchase order and the credit card

number. He sends the parcel weight and the customer address to the supplier. Finally a

shipper receives a parcel weight and a customer address. He returns a delivery date to

the received address.

The BPEL speciﬁcation and the mapping to π -calculus. In this example, we give the

BPEL speciﬁcation of the Seller which plays the role of a coordinator between the three

processes. The corresponding translation to π-calculus is also given. The veriﬁcation of

the correcteness of the example was made using the HAL Tool. The syntax used in this

tool is different from the standard one. The tool uses x?(y) to denote an input, x!y to

denote an output, k for the composition operator and (x)P to denote restriction. The

syntax of the other operators is standard. The correspondig π-calculus translation of

each BPEL component of our example is given by Table 5.

Finally the complete translation (simpliﬁed and optimized for veriﬁcation reasons)

is as follows :

The seller receives po, cc and M yChan on the channel c

, from the customer. He

sends the parcel weight w and a customer channel name z on the channel c

to the

shipper, or a fault name s

to the fault handler.

Seller(c

, c

, f ) = (w)(z)(s

)

?(po, cc, z).(c

!(w, z).y!˜u + f!s

))

In order to verify the correctness of the whole system, we need to specify the other

processes involved in the intercation. We abstract from details of the translation from

BPEL to π-calculus.

Table 5. Example of a mapping.

BPEL π-calculus

<invoke partner="customer" F H(f ) = f ?sr.y!u

portType="deliverPT"

operation="sendRefusal" fault handling

inputContainer="refusal"/>

</catch>

</faultHandlers>

The shipper receives a request from Buyer

<receive partner="customer", A

= (y)o?(po, cc, mc).y!u

portType="OrderPT",

operation="Order", o : channel for reception

variable="PurchaseOrder" po : Purchase Order

variable="CreditCardNumber" cc Credit card number

variable="MyChannel" mc Channel for response

He refers to shipper to get a Delivery date :

<invoke partnerLink="Shipper" A

= (to)(y)to!(w , rc) k rc?dd.y!u

operation="TransfertOrder"

inputVariable="DeliveryDate" to: operation

outputVariable="requestDelivery" rc : response channel

portType="requestDeliveryPT" /> w, dd: weigth and delivery date

He then sends the response to the customer :

<reply partner="customer", A

= (sd)(y)sd!dd k y!u

portType="delivrerPT",

operation="sendDeliveryDate", sd:operation

variable="DeliveryDate"/> dd:delivery date

<process name="ProcessOrder" P rocessOrder =

<faultHandlers .... /> (y

)(y

)(A

!u k y

?u.A

!u.y!u

</sequence>

π-calculus speciﬁcation of the entire system

The buyer sends a purchase order number po, a credit card number cc and a chan-

nel name M yChan to the company. He receives in response a delivery date d on the

channel MyChan. He can also send a fault name, b

, to the fault handler

Buyer(c

, MyChan, f) = (po)(cc)(My Chan)(b

)

!(po, cc, M yChan).(MyChan!d.y!(˜u) + f!b

))

The shipper receives a parcel weight and channel name He returns a delivery date

on the received channel. In case of error he sends a message ’delivery fail’, d

, to the

fault handler.

Shipper(c

, z, f) = (d)(d

)(c

?(w, z).(z!d.y!˜u + f !d

))

The fault Handler receives a fault name and processes it. It also need to cancel all

pending activities. To do this it sends a cancel message to the scope.

F aultHandler(n) = f?n.y!˜u

The whole system is represented as follows :

P rocessOrder() = (c

)(c

)(MyChan)

Buyer(c

, M yChan) k Seller(c

, c

) k Shipper(c

, z) k F aultHandler(n)

This example is an illustration of mobility and of the need for managing it since the

shipper does not know in advance the delivery address for the parcel.

From the formal speciﬁcation and by using an adequate model-checker, we can

check some properties of the system that prove its correctness.

5.4 Properties in π-logic

Here are for example, some temporal properties that assert of correct behavior of the

system described previously :

Let P

be the property : ”will the date of delivery be always sent to the customer

after he requests it?”.

We can express it as follows :

= AG([MyChan?d] ∧ EF ([M yChan!d]true))

And using the In HAL syntax :

P1 = AG([mc?d]EF<mc!d>true)

In the second example, let P

be the property : ”will the number of the credit card

never be revealed to other people but the salesman?”. We translate it in HAL syntax by :

P2 = AG([c1?cc]EF<c1!cc>true & <c2!cc>false)

6 A Framework for the Veriﬁcation of Web Services Compositions

We are actually working on the speciﬁcation and design of an environment for devel-

opping complex reliable composite Web services for which veriﬁcation tools will be

integral part. This platform should also be able to propose tools for ’reverse engineer-

ing’ i.e. the possibility of creating speciﬁcations in BPEL starting from formal models

expressed inπ-calculus.

We brieﬂy present, here, the architecture of the system being implemented and

which should enable us to check the relevance of the suggested concepts. An ambi-

tious objective is to design an integrated platform for composition of Web services.

This one will consist of:

– An editor for generic speciﬁcations (nonrelated to a particular language),

– A module for mapping of WSDL and BPEL (and other) speciﬁcations to π -calculus,

– A veriﬁcation tool : an interface with exisitng tools , MWB or HAL for instance,

– A tool for ’reverse engineering’ that allows designing real speciﬁcations from for-

mal deﬁnitions,

– A runtime environment.

Figure 1 shows the basic architecture of the veriﬁcation framework. Such an ap-

plication receives as input a speciﬁcation expressed in one of several BPM languages

(BPML, BPEL...) and rules (properties) that will be veriﬁed. The tool will make it pos-

sible to automatically translate these speciﬁcations into π-calculus processes. Properties

will be then checked, using an appropriate model-checker and in case of fault, a trace

of the faulty executions would be generated.

We are also interested in the study of equivalences between Web services. We are

developping and working on a complete theory of equivalence: deﬁnition, comparison

with bisimulation and algorithms. It is very important to check such equivalence that

decide of compatibilty between Web services, in order to substitute a service to another,

in case of fault or any other problem. Our environment aims to provide such tools.

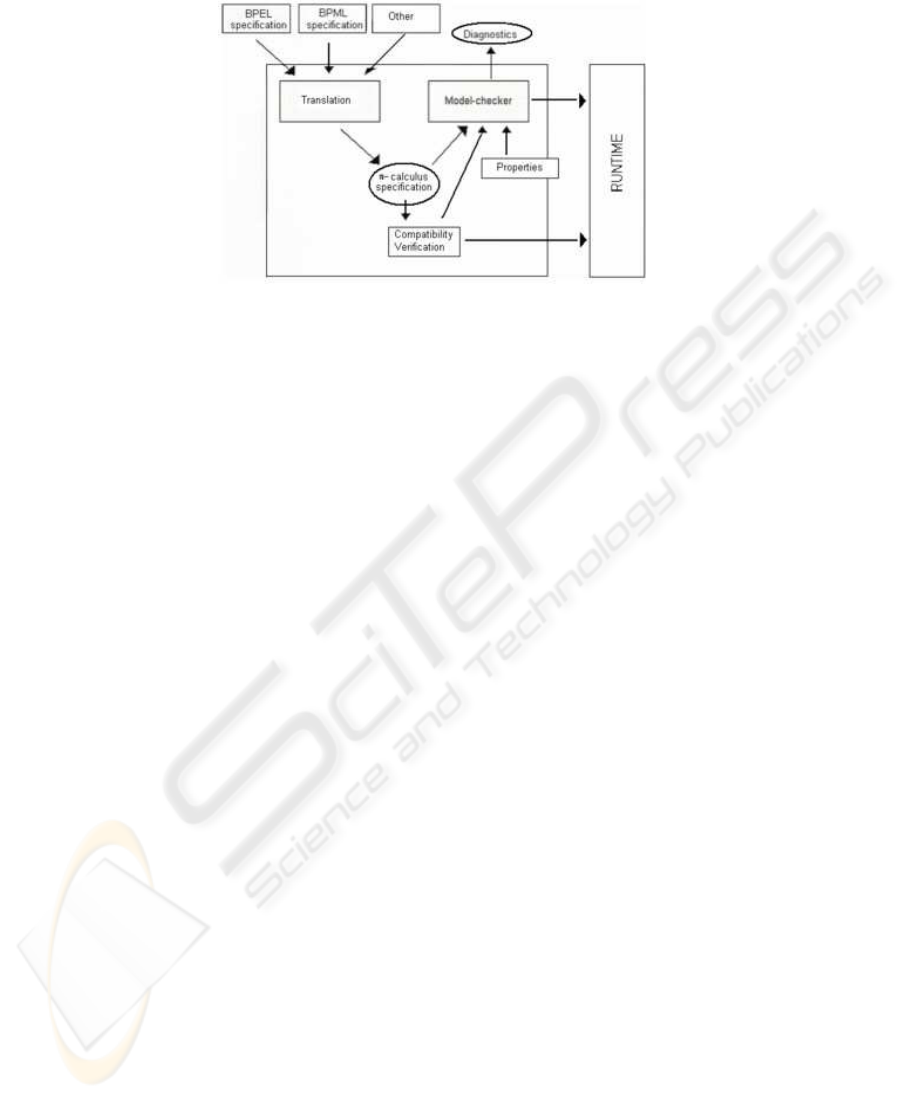
Fig.1. A Platform for Formal Veriﬁcation of Web Services Orchestrations.

7 Conclusion

Web services offer a remarkable potential of development. The problems are numerous,

in particular for the veriﬁcation of composite services behavior or equivalence between

services. The existing techniques can be adapted and used here. Petri nets or ASM

were studied and used abundantly in this context. However, because it allows specifying

mobility in an easy manner (it is possible to transmit channel names that then can be

used by any process receiving them) , and because compositional properties of process

are fundamental, the π-calculus is clearly shown to be a very suitable tool for Web

services formalization. We have shown with some examples that this aspect is essential

in formalization of orchestrations.

We have shown how a business process modelling language for Web services or-

chestrations can be modelled to a speciﬁcation language. We used BPEL as our BPM

language and the π-calculus as our target speciﬁcation language and therefore, we have

translated a program written in BPEL to a system model in the π-calculus. Once the

system model is achieved, it is possible to apply model checking techniques within

existing tools, thus, allowing an automatic veriﬁcation of BPEL speciﬁcations. Tech-

niques we have applied here for translating a BPEL speciﬁcation can be applied for any

BPM language for gaining a model in the π-calculus. We have also shown that the use

of analysis methods and tools based on this formal model (π-calculus) in some real life

setting, is not an evident task.

The goal of this paper has been to provide theroritical and concrete basis for the ar-

chitecture of an environment for analyzing Web services composition.This framework

integrates a tool for model-checking of speciﬁcations expressed in various languages

and a tool for ’ reverse engineering’ making it possible to conceive formal orchestra-

tions starting from formal speciﬁcation, expressed in the π-calculus. For its durability,

a signiﬁcant asset of such a tool is that it will have to be independant from any speci-

ﬁcation languages for orchestrations which are in perpetual evolution. For this purpose

we introduced a pi-based semantics for BPEL, inspired from [16] to express the main

construct of compositions languages. We have adapted the semantics to ﬁt the HAL

tool. This semantics allows us to specify systems from the real world and thus to verify

them, using model-checking techniques.

We consider this paper as the ﬁrst step towards the deﬁnition of a formal framework

for reasoning on orchestrations and choreographies. Several research directions open in

front of us. We are continuing our work by working on algorithm for mapping business

process speciﬁcations onto π-calculus instructions. We are also exploring ways to de-

ﬁne some behavioural equivalences on Web services that could be used to study their

compatibility. Finally and to complete this work, we have to take into consideration data

mapping.

References

1. Curbera, F., al.: Business process execution language for web services, version 1.0. Stan-

dards proposal, BEA Systems, International Business Machines Corporation, and Microsoft

Corporation, http://www-106.ibm.com/developerworks/library/ws-bpel/ (2003)

2. Kavantzas., N.: Aggregating web services: Choreography and ws-cdl. Technical re-

port, http://lists.w3.org/Archives/Public/www-archive/2004Jun/att-0008/WSCDL- April200

4.pdf (2004)

3. Hamadi, R., Benattallah, B.: A petri net based model for ws composition. In: In Proc.

Fourteenth Australasian Database Conference (ADC2003), Adelaide, Australia (2003)

4. Fahland, D.: Translate the informal bpel-semantics to a mathematical model: Abstract state

machines. Technical report, www.informatik.hu-berlin.de (2004)

5. Fu, X., Bultan, T., Su, J.: Analysis of interacting bpel web services. In: Proceedings of the

WWW2004, New-York, NY, USA (2004)

6. Brogi, A., Canal, C., Pimentel, E., Vallecillo, A.: Formalizing web service choreographies.

In Elsevier, ed.: Proceedings of First International Workshop on Web Services and Formal

Methods, Pisa, Italy (2004)

7. Van-Der-Aalst, W.: Pi calculus versus petri nets: Let us eat humble pie rather than further

inﬂate the pi hype. Technical report, Twente University, Nederland (2004)

8. Ferrara, A.: Web services: a process algebra approach,. In: Proceedings of the 2nd interna-

tional conference on Service oriented computing, New York, NY, USA (2004) 242–251

9. Milner, R.: Communication and Concurrency. Series in Computer Science. Prentice Hall

(1989)

10. Milner, R.: Communicating and Mobile Systems: The Pi-Calculus. Cambridge University

Press, Cambridge, UK (1999)

11. Milner, R., Parrow, J., D.Walker: Modal logics for mobile processes. Theoretical Computer

Science, (1993)

12. Dam, M.: Model checking mobile processes. In: In Proc. CONCUR’93, LNCS 715,

Springer-Verlag, Berlin (1993)

13. Hennessy, M., Milner, R.: Algebraic laws for nondeterminism and concurrency. Journal of

ACM (1985)

14. Ferrari, G., Gnesi, S., Montanari, U., Pistore, M.: A model checking veriﬁcation environ-

ment for mobile processes,. Technical report, Consiglio Nazionale delle Ricerche, Istituto di

Scienza e Tecnologie dell’Informazione ’A. Faedo’ (2003.)

15. Victor, B., Moller, F.: The mobility workbench - a tool for the π-calculus. In Springer-Verlag,

ed.: Proceedings of CAV’94. (1994)

16. Lucchi, R., Mazzara, M.: A pi-calculus based semantics for ws-bpel. Journal of Logic and

Algebraic Programming, Elsevier press (2005)